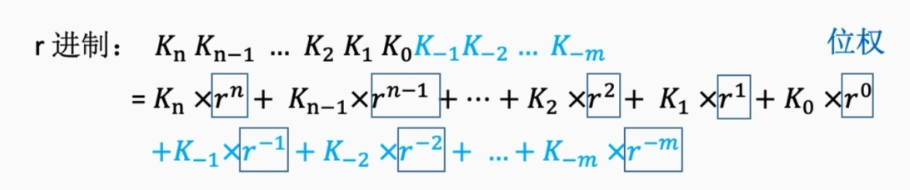数据的表示和运算

进位计数制

任意进制转为十进制

根据权值进行运算即可

image-20220306150022009

二进制和八进制，十六进制的相互转换

二进制转八进制，将二进制从低位到高位，3位一组，每组转换为对应的八进制符号即可

二进制转十六进制，将二进制从低位到高位，4位一组，每组转换为对应的十六进制符号即可

而反过来就是八进制，十六进制转换为二进制

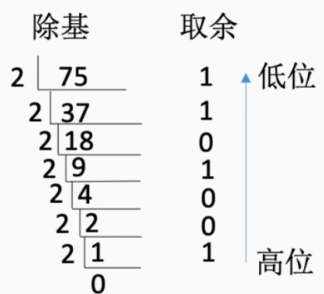
十进制转为任意进制

通用方法是使用除基取余法，但实际上一般用拼凑法

image-20220306150747121

真值和机器数

真值：实际带有正负号的数

机器数：把正负号数字化的数

字符与字符串

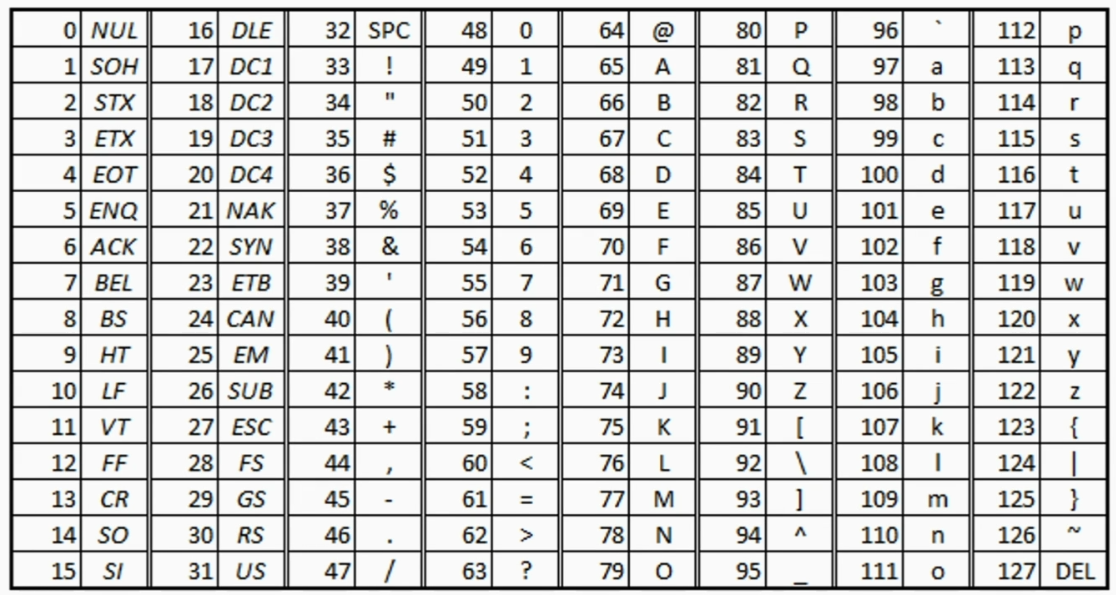
ASCII码

英文在计算机中通过ASCII码进行存储

image-20220306151604128

从32~126为可印刷字符，其余为控制，通信字符

汉字的存储

汉字的存储有多种方式，简单介绍一种GB 2312-80

先通过94×94的的表格存储汉字得到区位码

为了避免和ASCII码的前32位冲突，再将区位码+20H得到国标码

再将国标码+80H，得到汉字内码

字符串的存储

计算机按字节编址，从地址为2的单元开始，存储字符串，很多语言中用 \0 作为字符串结尾

而汉字占据两个字节，有两种存储模式，分别是将最高位有效字节存储在低地址单元的大端模式，和将最高位有效位存储在高地址单元的小端模式

定点数的表示

无符号数

无符号数：整个机器字长的全部二进制位均为数值位，没有符号位，相当于绝对值

8位二进制数可以表示$2^8$种不同状态

有符号数

有符号数：用最高位表示数的正负，称为有符号数

定点数：约定机器数中的小数点位置是固定不变的，一种在符号位的后面，称作定点小数，一种是在最低位之后，称作定点整数

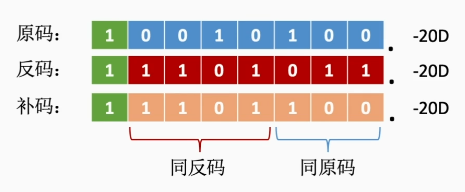
  1. 原码

    将最高位作为符号位，剩下的位来表示真值的绝对值，最高位为0表示正数，1表示负数

    如果机器字长为8位，原码整数可以表示的范围是：$-(2^7-1)$ ~ $(2^7-1)$

    真值0有2种形式，+0 和 -0

  2. 反码

    若符号位为0，则反码与原码相同，若符号位为1，则将原码的数值位全部取反得到反码
    表示范围和原码一样

  3. 补码

    正数的补码就是原码，负数的补码=反码末位+1（考虑进位）

    补码的0仅有一种形式 把1 0000 000 规定为$-2^7$

    补码整数表示范围是$-(2^7)$ ~ $(2^7-1)$

    负数补码转换为原码：将除符号位取反，末位+1

  4. 移码

    在补码的基础上将符号位取反，则是移码，移码相比于补码，可以更清晰的比较数的大小

补码的作用是将ALU中的减法操作转换为加法操作，就8位机器而言，其能表示的范围是-128~127，本质上可以看做是一个圆圈，从0开始到127,127接着是-128，然后又回到0，加法操作就是就是顺时针拨动，减法操作就是逆时针拨动

定点数的运算

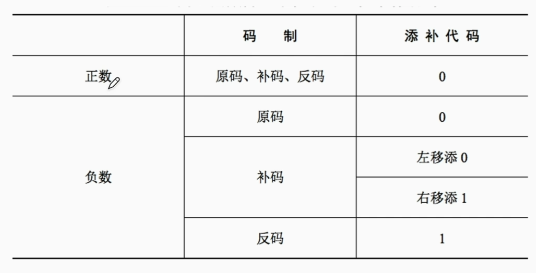
移位运算

移位：改变各个数码位和小数点的相对位置，从而改变各数码位的位权

算数移位：符号位保持不变，对数值位进行移位

  1. 原码

    右移：高位补0，低位舍弃。若舍弃的位是0，相当于÷2，若舍弃的位≠0，那么被舍弃后会丢失精度

    左移：低位补0，高位舍弃。若舍弃的位是0，相当于×2，若舍弃的位≠0，那么被舍弃后会出现严重误差

  2. 反码

    正数的反码和原码相同，因此对正数反码的移位运算也和原码相同

    负数的反码是对原码取反，所以对于负数反码来说，右移高位补1，左移低位补1

  3. 补码

    正数的补码和原码相同，因此对正数反码的移位运算也和原码相同

    对于负数的补码而言：

    右移：高位补1，低位舍弃

    左移：低位补0，高位舍弃
    image-20220308154237389

    因为在负数补码中，以最右边的1为分界，右边同原码，左边同反码

总结：

image-20220308154607072

逻辑移位：对所有位进行移位

右移：高位补0，低位舍弃

左移：低位补0，高位舍弃

循环移位

左移：所有位向左边移动，最低位移到最高位

右移：所有位向右边移动，最高位移到最低位

加减运算和溢出

原码的加减法

因为原码的符号位会影响运算，所以在涉及到正数和负数之间运算的时候需要用到绝对值和减法器

正+正 绝对值做加法

负+负 绝对值做加法，结果为负

正+负 绝对值大的减绝对值小的，符号同绝对值大的数

至于减法运算，把减数符号取反后，转变为加法就行

补码的加减法

对于补码来说，无论是加法还是减法，都是可以转换成补码做加法操作，符号位也要参与运算

溢出

正数+正数才有可能发生上溢（＞127）

负数+负数才有可能发生下溢 (< -128）

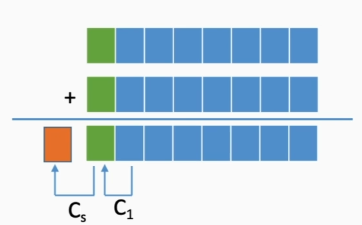
溢出判断

  1. 一位符号位

    $V=A_SB_S\bar{S}_S+\bar{A}_S\bar{B}_SS_S$

    A的符号位是$A_S$,B的符号位是$B_S$，运算结果的符号位是$S_S$

    V=0表示没有溢出，V=1表示有溢出

    当减法操作时，$A_S$=1，$B_S$=1，且$S_S$=0，会判断出溢出

    当加法操作时，$A_S$=0，$B_S$=0，且$S_S$=1，会判断出溢出

  1. 根据数据位进位情况判断

    image-20220308165630903

    发生上溢的时候：$C_1$=1 $C_S$=0

    发生下溢的时候：$C_1$=0 $C_S$=1

    $C_S$和$C_1$不同有溢出，用异或操作可以判断溢出，不同为1，相同为0

    $0\oplus 0=0$

    $0\oplus 1=1$

    异或结果为1，说明溢出

  1. 双符号位

    多加一个符号位，正数的符号位00，负数符号为11

    $S_1\oplus S_2=0$如果两个符号位相同则没有溢出，不同则溢出

符号拓展

当8位数据拓展到16位数据时，正数都加0，负数反码,补码加1,

相当于左移嘛

原码和补码的乘除运算

略

强制类型转换

C语言中的定点正数都是用“补码”形式存储的

如果要使用无符号数，要在数据类型前加上 unsigned

当有符号数转化成无符号数时，不会改变内容，而是改变解释方式

1
2
3
short x=-4321;                //short一般占用2个字节
unsighed short y=(unsigned short)x;
y=61213

长整数变为短整数时，会将高位截断，保留低位

1
2
3
int a=165537 ;// a:0x 000286a1
short c=(short) a;   // c: 0x 96a1
c=-31071

短整数变长整数时：会经历符号扩展，按补码的规矩，往高位添1

数据的存储和排列

多字节数据在内存中一定是占据连续的几个字节，有最高有效字节MSB，最低有效字节LSB

对于机器而言，通过小端方式，即让最低位占据在低地址，更便于机器处理数据

image-20220308202030774

现代计算机通常使用按字节编址（8bit），即每个字节对应1个地址，但也支持按字，半字，字节寻址

假设存储字长为32位，则1个字=32bit，半字=16bit，每次访存只能读取1个字

为了实现计算机内部的按字节，半字，字寻址，有两种数据排列方式

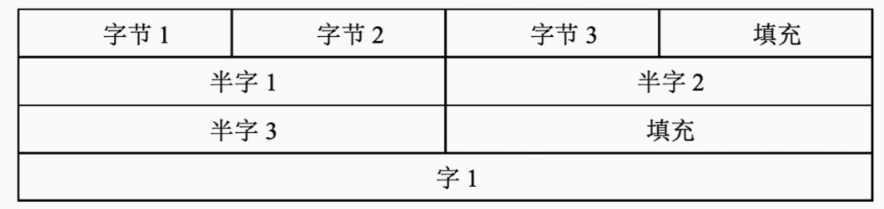
  1. 边界对齐方式

image-20220308204732745

让边界对齐，按字的来排列数据，空出的部分进行填充

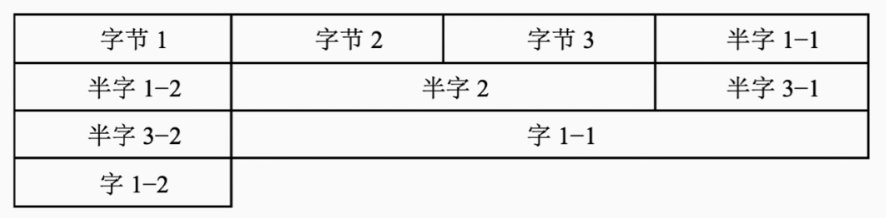
  1. 边界不对齐方式

image-20220308204958529

对数据进行紧凑的排布，不进行填充

边界对齐方式是一种用空间换时间的方式，因为每次访存只能读取一个字，边界对齐方式可以确保每次都能读取到完整数据

而边界不对齐方式是用时间换空间的方式，可以需要进行两次访存才能读取到完整数据

浮点数

浮点数的表示

定点数可以表示的数字范围是有限的，所以需要浮点数

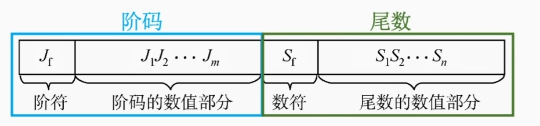
浮点数由阶码和尾数构成，阶码反映数值大小，尾数反映精度

利用十进制的科学计数法举例，$+123456789=1.234×10^8$，可以记作+8 +1.234 前面的+8就是阶码，+1.234是尾数，而10是底

image-20220309200920548

而在二进制中，阶码是常用补码或移码表示的定点整数，尾数是常用原码或补码表示的定点小数

浮点数的真值：

​ $N=r^E×M$

式中的 r 表示阶码的底，通常是2 ，E表示阶码，M表示尾数

比如 0,10；0.01001 分号前表示的是阶码，分号后表示的是尾数，假设阶码，尾数都用补码表示

0,10 逗号前是阶码的符号位，阶码是正数，表示2

0.01001 小数点前是尾数的符号位，尾数是正数，表示$(2^{-2}+2^{-5})$

所以b=$2^2×(0.01001)$，左移两位，结果是+1.001

假设存储空间只有1B，那么存储时就会丢失精度

image-20220309203941877

浮点数的规格化

在科学记数法中，规定用 $1≤|a|<10$ 的数来乘10的幂，在浮点数的表示中，自然也对尾数的形式有要求，称为浮点数的规格化

所以上节的问题，可以将$2^2×(0.01001)$规格化为$2^1×(0.1001)$

image-20220309211202071

左规：当浮点数运算的结果为非规格化时要进行规格化处理，将尾数算数左移移位，阶码减一

右规：当浮点数运算的结果尾数出现溢出（双符号位为01或10）时，将尾数右移一位，阶码加1

比如a=010；00.1100 b=010；00.1000

a+b的结果是$2^2×(00.1100+00.1000)=2^2×01.0100$，此时发生了溢出，可以右规，算数右移后，$2^3×00.1010$

不过以上的例子都是正数，如果是尾数是负数的话，就要考虑到使用原码还是补码进行规格化

对于原码来说，其尾数的小数点后最高位必须是1，对于补码来说，尾数的小数点后最高位必须是0

IEEE754

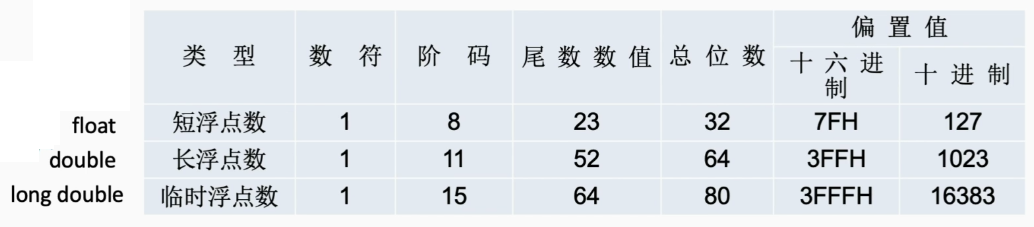
对于浮点数的表示，国际上有个统一的标准，称为IEEE754

IEEE754使用移码来表示阶码，移码=真值+偏置值

在IEEE中，偏置值为127D，即0111 1111B，是$2^{n-1}-1$

真值为-128，-128加上127，即是顺时针偏移127，结果是补码-1，1000 0001，原码表示是 1111 1111

真值为-127 -127+127=0000 0000

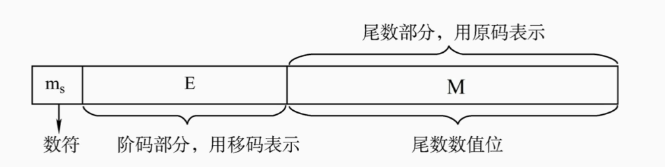
IEEE754中规定了浮点数的表示形式

image-20220310205028832

image-20220310205221185

最高位是数符，表示的是整个浮点数的正负

尾数用原码表示，默认了原码的最高位是1，所以有23位

阶码为-128，-127时有特殊用途，只能取到-126~127之间

规格化的短浮点数的真值是：$(-1)^s×1.M×2^{E-127}$

对于单精度浮点数来说，当尾数全为0，阶码真值最小为-126，移码为1，此时的最小绝对值为$(1.0)_2×2^{-126}$

最大绝对值是，当尾数全为1，阶码真值最大为254,，移码为127，此时的最大绝对值为$(1.11..11)_2×2^{127}$

如果表示值比最小的绝对值还要小，就要使用特殊方法

当阶码全为0，即真值为-127，但尾数M不全为0时，规定阶码为-126，表示非规格化小数 $±(0.xxx)_2×2^{-126}$

当阶码和尾数都是0，那就是表示0

当阶码全为1，尾数全为0时，表示无穷大 $∞$

当阶码全为1，尾数不全为0时，表示非数值，即非法运算

浮点数的运算

运算步骤

  1. 对阶，两个浮点数的阶不同时，让小阶向大阶对齐
  2. 尾数加减
  3. 规格化，保证尾数的最高位是有效位
  4. 舍入，舍入有很多规则，当要丢弃掉一些位时，可以四舍五入，或者全部丢弃
  5. 判断溢出 只有当阶码超过了两位情况下，才算发生了溢出，尾数溢出可以通过规格化来调整

浮点数的类型转换

精度从小到大不会发生溢出 char→int→long→double float→double

int和float同是32位，当时int表示整数，而float采用IEEE754标准表示整数及其小数，float能表示数的范围比int大得多

所以int→float：可能会损失精度，而float→int：既有可能发生溢出，也有可能损失精度

电路的基本原理

略