110.平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

img

1
2
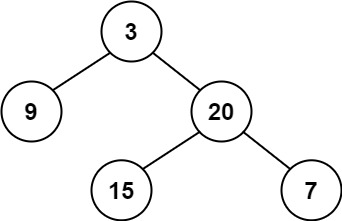
输入：root = [3,9,20,null,null,15,7]
输出：true

这种停止的递归的方法也挺有意思的，if (leftH == -1) return -1;

Solution

如何判断一棵二叉树是否平衡呢？需要比较其子树的深度差，采取从底向上的遍历方法，如果其子树不是平衡二叉树，那么会返回-1，如果是，那么就返回他的最大深度，只要结点的左子树，右子树，或者左右高度差大于1满足一个条件，就会返回-1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    // 私有辅助方法，用于递归计算树的高度，同时检查树是否平衡。
    private int getHeight(TreeNode node) {
        // 基础情况：如果节点为空，则高度为0。
        if (node == null) return 0;

        // 递归地获取左子树的高度。
        int leftH = getHeight(node.left);
        // 如果左子树不平衡，则直接返回-1，表示不平衡。
        if (leftH == -1) return -1; // 提前退出，不再递归

        // 递归地获取右子树的高度。
        int rightH = getHeight(node.right);
        // 如果右子树不平衡，或左右子树的高度差超过1，则返回-1，表示不平衡。
        if (rightH == -1 || Math.abs(leftH - rightH) > 1) return -1;

        // 如果当前节点的子树都平衡，返回当前树的高度，高度是左右子树的最大高度加1。
        return Math.max(leftH, rightH) + 1;
    }

    // 公共方法，用于判断二叉树是否平衡。
    public boolean isBalanced(TreeNode root) {
        // 调用getHeight方法，如果返回值不是-1，则树平衡。
        return getHeight(root) != -1;
    }
}