481.神奇字符串

神奇字符串 s 仅由 '1' 和 '2' 组成，并需要遵守下面的规则：

  • 神奇字符串 s 的神奇之处在于，串联字符串中 '1' 和 '2' 的连续出现次数可以生成该字符串。

s 的前几个元素是 s = "1221121221221121122……" 。如果将 s 中连续的若干 1 和 2 进行分组，可以得到 "1 22 11 2 1 22 1 22 11 2 11 22 ......" 。每组中 1 或者 2 的出现次数分别是 "1 2 2 1 1 2 1 2 2 1 2 2 ......" 。上面的出现次数正是 s 自身。

给你一个整数 n ，返回在神奇字符串 s 的前 n 个数字中 1 的数目。

示例 1：

1
2
3
输入：n = 6
输出：3
解释：神奇字符串 s 的前 6 个元素是 “122112”，它包含三个 1，因此返回 3 。

Solution

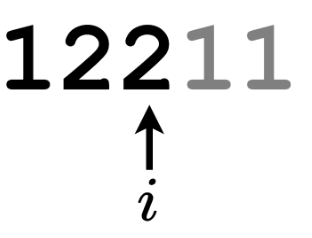
image-20240423215440572

根据题意，我们可以把 s看成是由「111 组」和「222 组」交替组成的，重点在于每组内的数字是一个还是两个，这可以从 s 自身上知道。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int magicalString(int n) {
        char[] s = new char[n + 2];
        s[0] = 1; s[1] = s[2] = 2;
        char c = 2;
        int i = 2, j = 3; // 初始化索引 i 和 j
        while (j < n) {   // 循环直到 j 达到 n
         c ^= 3;       // 切换字符 c 在 1 和 2 之间
         s[j++] = c;   // 将字符 c 存储到数组 s 的 j 位置，并增加 j

         if (s[i] == 2) { // 检查 s[i] 是否为 2
         s[j++] = c; // 如果是，再次将字符 c 存储到数组 s 的 j 位置，并增加 j
                         }

         i++;           // 增加 i 用于下一轮检查
     }

        int ans = 0;
        for (int i = 0; i < n; ++i) ans += 2 - s[i]; // 2-1=1，2-2=0，这样就只统计了 1
        return ans;
    }
}