栈和队列
栈
逻辑结构
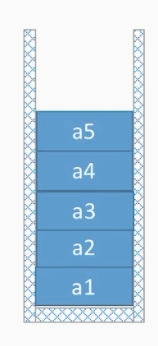
栈是只允许在一端进行插入和删除操作的线性表
特点是先进后出
n个不同元素进栈,出栈元素不同排列的个数为$\frac{1}{n+1}C^n_{2n}$(卡特兰数)
基本操作
创建,元素进栈,出栈,获取栈顶元素
存储结构
顺序栈
定义
1
2
3
4
| typedef struct {
int data[MaxSize];
int top;
}SqStack;
|
初始化
1
2
3
4
| void InitStack(SqStack *S)
{
S->top=0;
}
|
进栈
1
2
3
4
| void Push(SqStack* S, int x) {
S->data[S->top] = x;
S->top++;
}
|
出栈
1
2
3
4
| void Pop(SqStack* S,int x) {
S->top--;
x = S->data[S->top];
}
|
读取栈顶元素
1
2
3
4
5
| void gettop(SqStack* S,int x) {
int t=S->top-1
x = S->data[t];
return x;
}
|
链式栈
头插法创建链表就是链式栈
队列
逻辑结构
队列是只允许在一端进行插入,在另一端进行删除的线性表
特点是先进先出

基本操作
创建,初始化,入队,出队,读队头元素
存储结构
顺序队列
定义
1
2
3
4
| typedef struct {
int data[MaxSize];
int front, rear;
}SqQueue;
|
初始化
1
2
3
4
5
| void Init(SqQueue* q)
{
q->front = 0;
q->rear = 0;
}
|
入队
(以下是队尾指针指向队尾元素的后一个位置,如果队尾指针指向队尾元素,就要先让队尾指针+1,再进行插入操作)
1
2
3
4
| void Insert(SqQueue *q,int x) {
q->data[q->rear] = x;
q->rear = q->rear + 1;
}
|
出队
1
2
3
4
5
6
7
8
9
|
void DeQueue(SqQueue* q,int *x) {
if (((q->rear) + 1) % MaxSize == q->front) {
printf("full");
}
x = q->data[q->front];
q->front = (q->front + 1) % MaxSize;
}
|
队满:
(q->rear) + 1) % MaxSize == q->front
队空:
q->rear == q->front
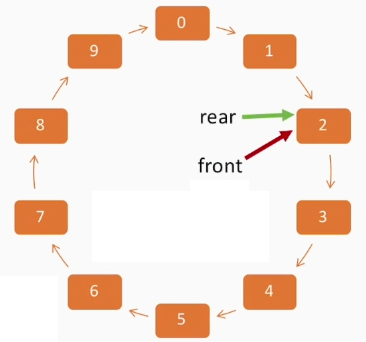
为了区别队空和队满时的状态,除了牺牲一个空间以外,也可以用标志位tag进行判断
链式队列

定义
1
2
3
4
5
6
7
8
| typedef struct LinkNode{
ElemType data ;
struct LinkNode *next;
}LinkNode;
typedef struct {
LinkNode *front,*rear;
}LinkQueue
|
初始化
1
2
3
4
5
| void InitQueue(LinkQueue &Q){
Q.front=Q.rear=(LinkNode*)malloc(sizeof(LinkNode));
Q.front->next=null;
}
|
入队
1
2
3
4
5
6
7
| void EnQueue(LinkQueue &Q,ElemType x){
LinkNode *s=(LinkNode *)malloc (sizeof(LinkNode));
s->data=x;
s->next=NULL;
Q.rear->next=s;
Q.rear=s;
}
|
出队
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| bool DeQueue (LinkQueue &Q,ElemType &x){
if(Q.front==Q.rear){
return false;
}
LinKNode *p=Q.front->next;
x=p->data;
Q.front->next=p->next;
if(Q.rear==p)
{
Q.rear=Q.front;
}
return true;
}
|
链式一般不会队满,所以不需要考虑
双端队列
允许从双端插入,双端删除的队列
栈和队列的应用
栈和队列相对来说应用较少,栈一般用来解决成对元素消去的问题
括号匹配问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| char pairs(char a) {
if (a == '}') return '{';
if (a == ']') return '[';
if (a == ')') return '(';
return 0;
}
bool isValid(char* s) {
int n = strlen(s);
if (n % 2 == 1) {
return false;
}
int stk[n + 1], top = 0;
for (int i = 0; i < n; i++) {
char ch = pairs(s[i]);
if (ch) {
if (top == 0 || stk[top - 1] != ch) {
return false;
}
top--;
} else {
stk[top++] = s[i];
}
}
return top == 0;
}
|
中缀转为后缀表达式
算数表达式由操作数(数字),运算符(+ - × ÷),界限符(括号)组成
运算符在两个操作数后面就称为后缀表达式
手算:
先确定中缀表达式中各个运算符的运算顺序,
选择下一个运算符,按照[左操作数 右操作数 运算符]的方式组成一个新的操作数
机算:
遇到左括号直接入栈,遇到右括号将栈中左括号之后入栈的运算符全部弹栈输出,同时左括号出栈但是不输出。
遇到乘号和除号直接入栈,直到遇到优先级比它更低的运算符,依次弹栈。
遇到加号和减号,如果此时栈空,则直接入栈,否则,将栈中优先级高的运算符依次弹栈(注意:加号和减号属于同一个优先级,所以也依次弹栈)直到栈空或则遇到左括号为止,停止弹栈。(因为左括号要匹配右括号时才弹出)。
获取完后,将栈中剩余的运算符号依次弹栈输出
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
void Change(SqStack *S,Elemtype str[])
{
int i=0;
Elemtype e;
InitStack(S);
while(str[i]!='\0')
{
while(isdigit(str[i]))
{
printf("%c",str[i++]);
if(!isdigit(str[i]))
{
printf(" ");
}
}
if(str[i]=='+'||str[i]=='-')
{
if(!StackLength(S))
{
PushStack(S,str[i]);
}
else
{
do
{
PopStack(S,&e);
if(e=='(')
{
PushStack(S,e);
}
else
{
printf("%c ",e);
}
}while( StackLength(S) && e != '(' );
PushStack(S,str[i]);
}
}
else if(str[i]==')')
{
PopStack(S,&e);
while(e!='(')
{
printf("%c ",e);
PopStack(S,&e);
}
}
else if(str[i]=='*'||str[i]=='/'||str[i]=='(')
{
PushStack(S,str[i]);
}
else if(str[i]=='\0')
{
break;
}
else
{
printf("\n输入格式错误!\n");
return ;
}
i++;
}
while(StackLength(S))
{
PopStack(S,&e);
printf("%c ",e);
}
}
|
后缀表达式求值
- 从左往右扫描下一个元素,直到处理完所有元素
- 若扫描到操作数则压入栈
- 若扫描到运算符,则弹出两个栈顶元素,执行相应运算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| bool isNumber(char* token) {
return strlen(token) > 1 || ('0' <= token[0] && token[0] <= '9');
}
int evalRPN(char** tokens, int tokensSize) {
int n = tokensSize;
int stk[n], top = 0;
for (int i = 0; i < n; i++) {
char* token = tokens[i];
if (isNumber(token)) {
stk[top++] = atoi(token);
} else {
int num2 = stk[--top];
int num1 = stk[--top];
switch (token[0]) {
case '+':
stk[top++] = num1 + num2;
break;
case '-':
stk[top++] = num1 - num2;
break;
case '*':
stk[top++] = num1 * num2;
break;
case '/':
stk[top++] = num1 / num2;
break;
}
}
}
return stk[top - 1];
}
|
特殊矩阵的压缩
对称矩阵
若n阶方阵中任意一个元素都有$a_{i,j}=a_{j,i}$,则改矩阵为对称矩阵
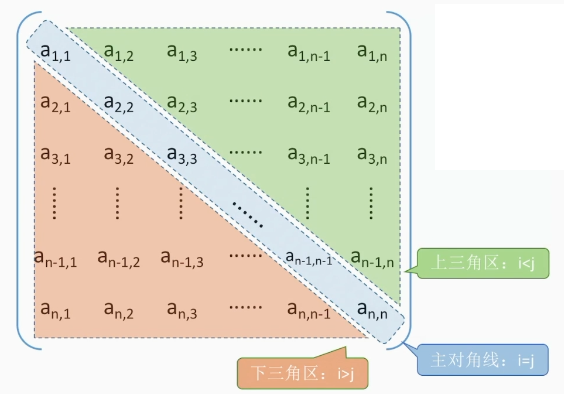
可以按行优先原则,只存储主对角线和下三角的元素,用一个大小为$\frac{n(n+1)}{2}$的数组来存储
$a_{i,j}$对应的就是数组中第$\frac{i(i-1)}{2}+j$个元素,下标在此基础上-1
(不需要背公式,主要是理解存储顺序以及下标需要-1)
三角矩阵
除了主对角区和上(下)三角区,其余的元素都相同
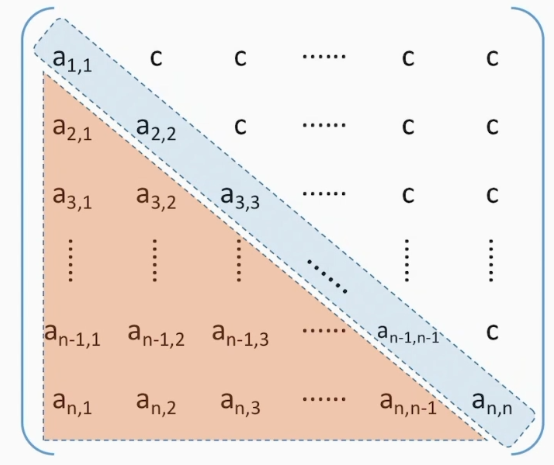
相比与对称矩阵,三角矩阵需要空间为$\frac{n(n+1)}{2}+1$,多一个空间用于最后存放c这个常量
三对角矩阵
当$|i-j|>1$时,有$a_{i,j=0}$
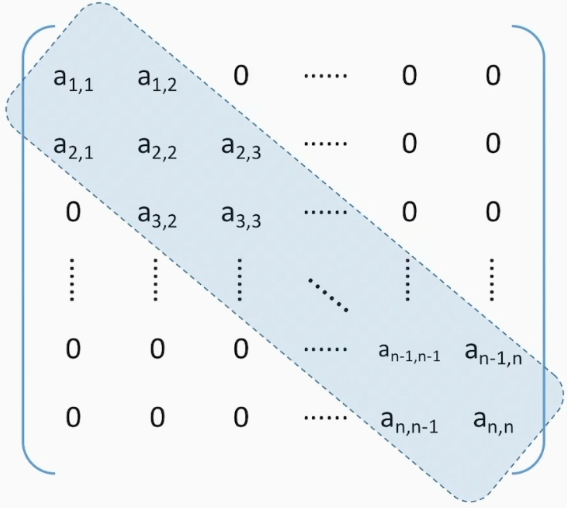
需要大小为3n-2的数组,前i-1行共3(i-1)-1个元素,$a_{i,j}$是第i行第j-i+2个元素
所以$a_{i,j}$是第2i+j-2个元素
稀疏矩阵
非零元素远远少于矩阵元素的个数
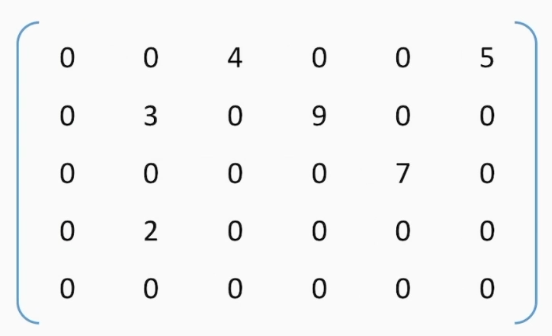
使用三元组,即i行 j列 v值的方法存储
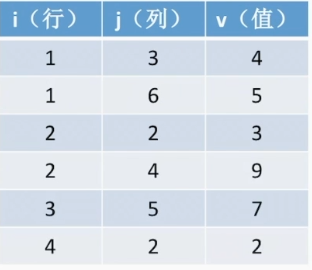
假设矩阵中有X个非零元素,除了需要X个三元组之外,还需要一个三元组记录当前矩阵的行数,列数,非零元素个数
也可以使用十字链表法











