字符串

字符串是由零个或多个字符组成的有限序列

字符的个数n就是字符串的长度，n=0时称为空串

逻辑结构

串是一种特殊的线性表，数据元素之间呈线性关系

image-20220507203329378

基本操作

赋值，复制，求串的长度，连接串，求子串，定位，比较

存储结构

顺序存储

字符串是线性表，所以可以用顺序存储的方式，就是在定义中，把数组的类型规定为char类型即可

1
2
3
4
5
6
//结构体定义 
typedef struct 
{
	char *data;  //存放顺序表元素的数组 
	int length; //存放顺序表的长度 
 }Sqlist;		//顺序表类型的定义

链式存储

同理也可以使用链式存储

1
2
3
4
5
6
//链表的定义
typedef struct  Node
{
	char data;
	struct Node* NEXT;
}Node, *LinkList;

不过这样的存储密度很低，建议每个结点存储多个字符

1
2
3
4
5
6
//链表的定义
typedef struct  Node
{
	char data[4];
	struct Node* NEXT;
}Node, *LinkList;

字符串的模式匹配

在主串中找到与模式串相同的子串，并返回其所在位置

朴素模式匹配算法

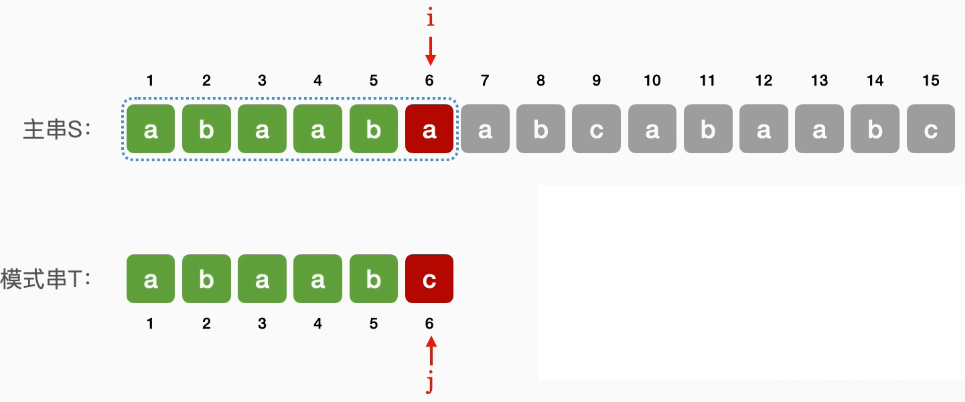
image-20220507211122668

主串长度为n，模式串长度为m

朴素模式匹配算法：将主串中所有长度为m的子串依次与模式串对比，直到找到一个完全匹配的子串或所有的子串都不匹配为止。（很朴素）

如果子串匹配失败，则主串指针指向下一个子串的第一个位置，模式串指针回到模式串第一个位置

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <stdio.h>
#include <string.h>
#define maxsize 100

int Index_BF(char S[],char T[])
{
	int i=0,j=0;
	while(S[i]!='\0'&&T[j]!='\0')//S[i]=='\0'则为匹配失败，T[i]==‘\0’为匹配成功！
	{
		if(S[i]==T[j])  //某一字符匹配成功
		{
			i++;
			j++;
		}
		else
		{
			i=i-j+1;//i回溯到下一位置
			j=0;//j回溯
		}
	}
	if(T[j]=='\0')//对应上面循环条件匹配成功
	{
		printf("Match succeed!\n");
		return i-j; //返回第一位的下标
	}
	else//对应上面循环条件S[i]=='\0'匹配失败
	{
		printf("Match failed!\n");
		return -1;
	}
}


代码很容易理解，注意一点，i和j的默认是0，而王道上默认是1，其实都可以，不过默认是0的方便一点

主串长度为n，模式串长度为m，最坏的时间复杂度是O(mn)，最好时间复杂度是O(n)

KMP算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，简称KMP算法。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个NEXT()函数实现，函数本身包含了模式串的局部匹配信息

KMP算法是基于朴素算法的，对比朴素识别和KMP算法：

image-20220508194629894

最大的差别在于，else里面的j=NEXT[j]，也就是匹配失败后，i不会回溯，而是j回溯到NEXT[j]的位置，而不是从0开始

而KMP的核心正是利用NEXT数组来存储匹配失败后的信息以减少匹配次数

而求取NEXT数组的值，成为了KMP算法的关键

在此之间，需要先介绍“”最大长度“”Length数组，该数组的作用是用来存放一个字符串的最长前缀和最长后缀相同的长度，按每一位下标将对应长度值存于数组Length中

比如模式串“ababaca”的Length数组就是{0，0，1，2，3，0，1}

之所以需要这个Length数组，是因为Length数组的下标与模式串T的下标是一致的（也就是下标 j），也就是模式串T中每一位都可以对应其下标j在Length数组中找到该位当前前缀与后缀的最长匹配长度，那么也就知道了，在当前位置下（也就是后缀）是否与模式串的开头（也就是前缀）有相同的部分、相同的部分是几位，这就是利用前缀匹配失败的信息

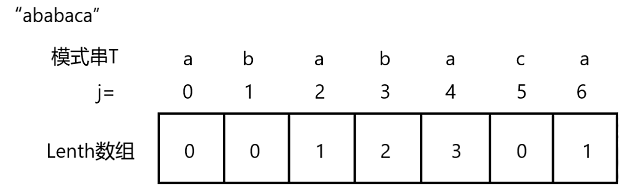
image-20220508205033697

那么也就是说，有了Length数组，我们只需要知道下标就可以知道，当前的前后缀的最长匹配长度。而当j位发生不匹配，需要回溯时，我们要看前一位也就是j-1位的前后缀匹配情况也就是Length[j-1]，可以知道要从j位回溯到Length[j-1]位

但是，有个问题，第j位的回溯位置需要看第j-1位的信息，为了让第j位的回溯信息可以直接到第j位去找，我们可以把Length数组整体后移一位，这就是NEXT数组

image-20220508205735375

  • NEXT数组也正是KMP算法的精髓所在，充分记录并利用探路人（后缀）获取的信息（已匹配信息），让算法能绕过很多不必要的匹配项，少走很多弯路

image-20220508210350464

观察求NEXT数组的代码，可以发现，与KMP算法的代码相似性极高，那么其实求NEXT数组就是让模式串T的前缀和后缀相匹配，那么也就是一个自我匹配的过程，用前缀去匹配后缀。

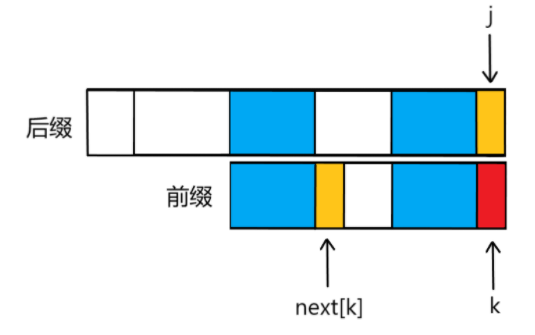
那么不同之处在于当匹配成功时，我们不但要把指针（下标）向后推一位，还同时需要对应当前下标记录下当前的最佳匹配长度，也就是NEXT[j]=k,表示的是模式串T的前缀的前k项与后缀的前k项相匹配，那么k也正是当前的匹配长度

而先j++后将k的值存放在NEXT数组中，正好对应了将Length数组右移一位变成NEXT数组的过程

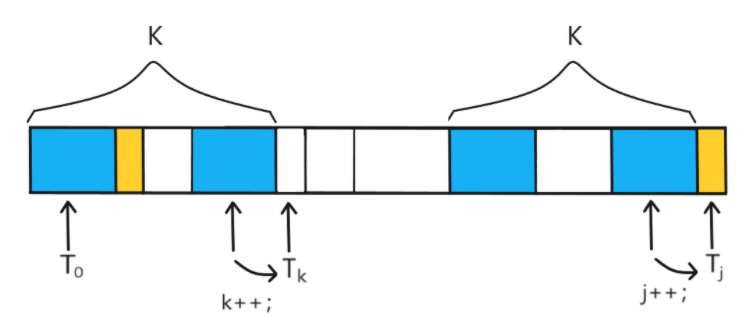
image-20220508214230678

同时k++，j++，的原因也很简单，既然模式串T的前缀的前k项与后缀的前k项，那么k+1项和j+1项会不会也匹配？

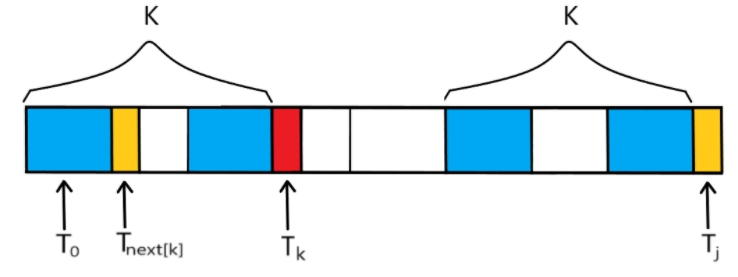
image-20220508214316318

如果在前k项与后k项相同的情况下，第k+1项失配，也就是下图所视情况，T[k]≠T[j] ，那么我们的前缀指针k是不是要回溯，在此处使用BF算法的回溯思路，从零开始重新找前后缀匹配长度，固然可以，但是我们如果用kmp算法的回溯思路，是不是可以更快找到呢？

为什么在NEXT数组没有完全成型之前就用NEXT数组来回溯呢，因为在求NEXT数组的算法中，K永远比J小

image-20220508214556007

算法漏洞

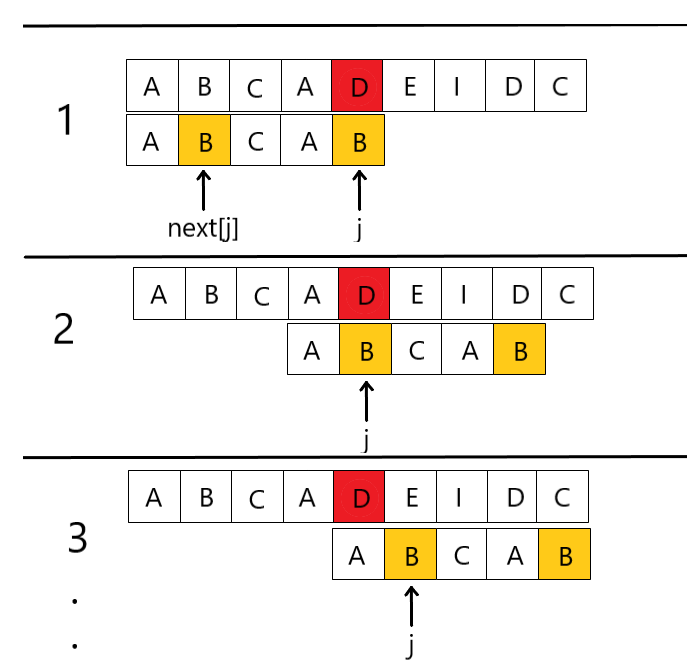
image-20220508214955963

我们发现这个算法其实还是存在漏洞，如下图的情况，第2步的情况是完全没有必要的，因为在第1步时已经判断过“B”≠”D”,第2步又判断了一次“B”≠”D”。那有没有办法可以省掉，或者是跳过这个多余步骤呢？

其实我们只需要加一个判断就可以了，当if判断完前k项与后k项相匹配后，j++；k++;此时j和k都向后推了一位，分别指向下一位，那么这时我们不着急记录长度k于NEXT数组，而是加一个判断，预判断一下下一位（这里的下一位是指j++；k++;之前的下一位）是否相等，也就是T[j]与T[k]是否相等，如果不相等，我们记录k的值于NEXT数组；如果相等的话，就会出现上述多余重复匹配的现象，那么我们在这里通过连续的两次回溯，来跳过它，也就是k = NEXT[NEXT[k]];(NEXT[j]=NEXT[k];将NEXT[k]的值存于NEXT[j]也是一样的道理），回溯完之后不进行匹配判断就进行下一次回溯，即是跳过了他的匹配步骤

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <stdio.h>
#include <string.h>
#define maxsize 100 

void Nextval(char T[],int *next)
{
	int lenT=strlen(T);
	int k=-1;//前缀 
	int j=0;//后缀 
	next[0]=-1; 
	
	while(j<lenT)
	{
		if(k==-1||T[j]==T[k])
		{
			j++;
			k++;
			//较之前next数组求法，改动在下面4行
			if(T[j]!=T[k])
			{
			next[j]=k;//之前只有这一行
			}
			else
			{
			next[j]=next[k];//为不能出现T[j] = T[ next[j ]]，
				            //所以当出现时连续进行两次回溯，k = next[next[k]] 
			 } 
		}
		else 
		{
		k=next[k];
		} 
	}
}

int KMP(char S[],char T[])
{
	int i=0,j=0,lenS,lenT;
	lenS=strlen(S);
	lenT=strlen(T);
	
	int next[maxsize];
	Nextval(T,next);
	
	while(i<lenS&&j<lenT)
	{
		if(j==-1||S[i]==T[j])
		{
			i++;
			j++;
		}
		else
		{ 
			j=next[j];
		}
	}
	 
	if(j==lenT)
	{   
	    printf("Match succeed!\n");
	 	return i-j;
	} 
	else 
	{
		printf("Match failed!\n");
		return -1;
    }
}


int main() 
{
    char S[maxsize],T[maxsize];
    int target;
	
	strcpy(S,"AAAAAAAAAAttract");
	strcpy(T,"Attract");

	target=KMP(S,T);
	printf("Position is %d\n",target);
	return 0;
}