142.环形链表2

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

1
2
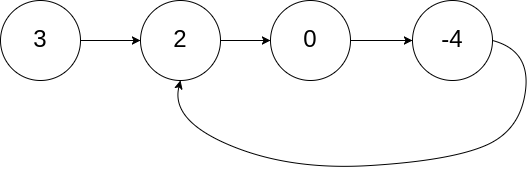
3

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

1
2
3

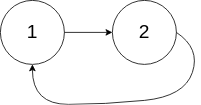
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

1
2
3

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

哈希表的解法太简单了，应该使用快慢指针

Solution

算法中快慢指针相遇点和环入口点之间的距离关系，关键的理解是这样的：

快慢指针首次相遇时，我们可以得到如下关系：当快慢指针相遇时，假设慢指针从链表起点走了 ( $L$ ) 步，那么快指针则走了 ( $2L$ ) 步（因为快指针的速度是慢指针的两倍）

设：

fig1

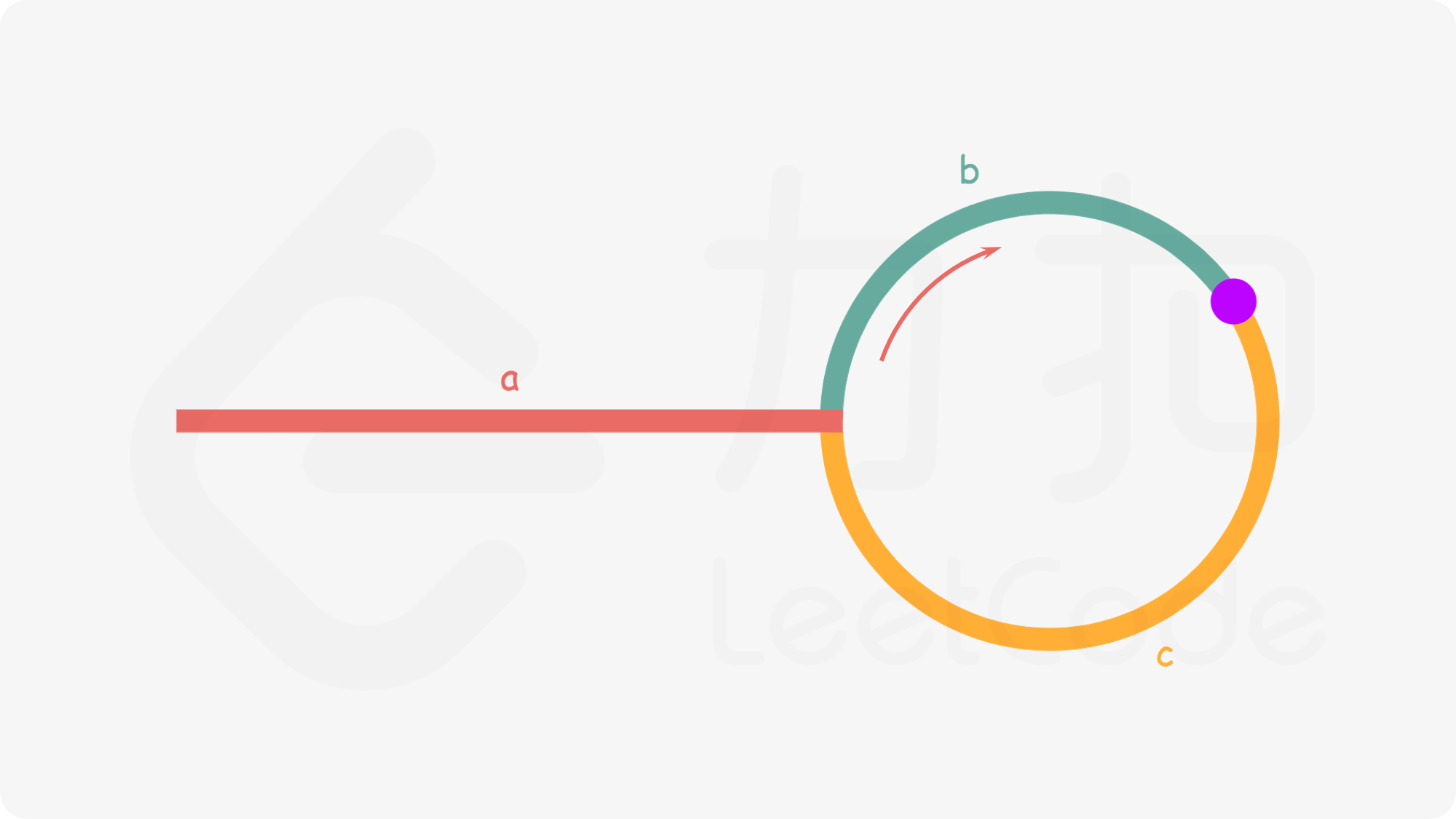
a 是从链表起点到环入口点的距离。
b 是从环入口点到快慢指针相遇点的距离。
c 是从快慢指针相遇点回到环入口点的距离。

我们可以列出以下等式来描述快慢指针的行走：

慢指针走的总距离：$( a + b)$
快指针走的总距离：$( a + b + n(b + c) )$ 其中 $( n )$ 是快指针在环内走的完整圈数。

因为快指针走的距离是慢指针的两倍，所以：

$a + b + n(b + c) = 2(a + b)$

解这个等式，我们得到：

$a = (n - 1)(b + c) + c$

这里的关键点是：从链表起点到环入口的距离 ( $a$ ) 等于从相遇点回到环入口的距离 ( $c$ ) 加上 ( $n-1$ ) 圈环的长度。实际上就是$a=c$，因为$n$可以取任何值！

所以移动相同地的距离，最后会在入口处相遇

// 定义Solution类
public class Solution {
    // detectCycle方法用来检测链表中的环，并返回环的起始节点
    public ListNode detectCycle(ListNode head) {
        // 如果头节点为空，则链表也为空，没有环
        if (head == null) {
            return null;
        }
        // 定义快慢指针，初始都指向头节点
        ListNode slow = head, fast = head;
        // 循环直到快指针遇到null，即链表结束
        while (fast != null) {
            slow = slow.next; // 慢指针每次移动一步
            if (fast.next != null) {
                fast = fast.next.next; // 快指针每次移动两步
            } else {
                return null; // 如果快指针遇到链表末尾，说明没有环
            }
            // 如果快慢指针相遇，说明存在环
            if (fast == slow) {
                // 创建一个新的指针ptr，初始指向头节点
                ListNode ptr = head;
                // 移动ptr和slow，直到它们相遇，相遇点即为环的起始节点
                while (ptr != slow) {
                    ptr = ptr.next;
                    slow = slow.next;
                }
                // 返回环的起始节点
                return ptr;
            }
        }
        // 如果快指针走到了链表尾部都没有与慢指针相遇，说明没有环
        return null;
    }
}