查找

在数据集合中寻找满足某种条件的数据元素的过程称为查找

平均查找长度：所有查找过程中进行关键字的比较次数的平均值

顺序查找

就是从头到尾依次查找

1
2
3
4
5
6
7
8
9
10
11
12
typedef struct{
 int *elem;
 int  length;
}table
int Search_Seq(table st,int key){
    for(int i=0;i<length;i++){
        if(s[i]==key){
            return i;
        } 
    }
    return -1;
}

也可以添加“哨兵“，就不必担心越界问题

如果查找的是有序表的话，如果查找到比关键字大的数的话，可提前结束查找

时间复杂度：O(n)

二分查找

仅适用于有序的顺序表，每次查找从顺序表的一半开始

image-20220524142406209

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
typedef struct{
 int *elem;
 int  length;
}table
    
int BinarySearch(table st,int key){
int mid,high,low;
high=st.length-1;
low=0;
whlie(low<=high){
mid=(low+high)/2;
    if(st.elem[mid]==key){
     return mid;
    }else if(L.elem[mid]>key)
        high=mid-1; 
    else
        low=mid+1
}
    return -1；
}

折半查找如果是向下取整，则判定树的右子树结点数-左子树结点数=0或1，折半查找如果是向上取整，则判定树的左子树结点数-右子树结点数=0或1

观察树形是否是折半查找判定树，需要注意一整树的所有结点是否都符合左子树≥右子树或右子树≥左子树的规律(注意是结点数，而非平衡因子)

判定树高为$log_2(n+1)$

时间复杂度：$O(log_2n)$

分块查找

建立索引表，保存每个分块的最大关键字和分块的存储区间

1
2
3
4
5
6
typedef struct {
    ElemType maxValue;
    int low,high;
}Index;
Elemtype list[100];

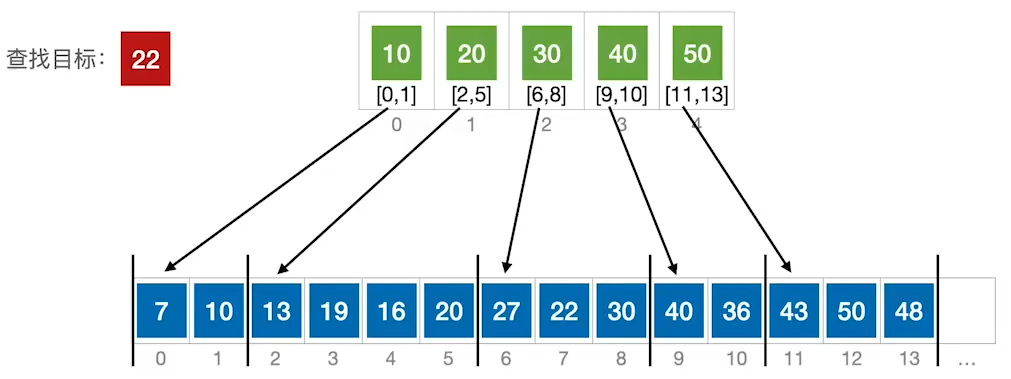
image-20220524145733262

在索引表中确定待查记录所属的分块（可顺序，可折半），在块内顺序查找

若索引表中不包含目标关键字，则折半查找索引表最终停在了low>high，要在low的分块中查找

如果长度为n的查找表被均匀地分为了b块，每块s个元素

$ASL=L_1+L_S$，当$s=\sqrt{n}$时，$ASL$有最小值$\sqrt{n}+1$

二叉排序树（BST）

之前介绍过，是左节点值<根节点值<右节点值

查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//在二叉排序树T中查找包含关键字key的元素的结点 
BSTree SearchBST(const BSTree T, int  k) {
    BSTree p = T;
    while (p) {
        if (k == p->data ) {
            return p;//查找成功 
        }
        if (k < p->data ) {
            p = p->Lchild;
        }
        else {
            p = p->Rchild;
        }
    }
    return NULL;//查找失败，返回空值 
}

插入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
void InsertBST(BSTree* treePtr, int value)
{

    /* 初始化根节点*/
    if (*treePtr == NULL) {

        *treePtr = malloc(sizeof(BSTNode));

        if (*treePtr != NULL) {
            (*treePtr)->data = value;
            (*treePtr)->Lchild = NULL;
            (*treePtr)->Rchild = NULL;
        }
        else {
            printf("%d not inserted. No memory available.\n", value);
        }
    }
    // 递归实现
    else {

        /* 在左子树中插入 */
        if (value < (*treePtr)->data) {
            InsertBST(&((*treePtr)->Lchild), value);
        }
        else {

        /* 在右子树中插入*/
            if (value > (*treePtr)->data) {
                InsertBST(&((*treePtr)->Rchild), value);
            }
            else {
                printf("the element is exists");
            }
        }
    }
}

删除

有多种情况

  1. 如果是叶子结点，那么直接删除即可
  2. 如果是只有一棵子树，那么让子树代替即可
  3. 如果有两棵子树，那么需要找到被删除结点的直接前驱或后继，代替其位置即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
BSTree DeleteBST(BSTree T, int  k) {
    //BSTree p, fatherp, fatherpre, pre;//设指针p指向待删除的节点，q为p的父节点指针
                   //pre为p的直接前驱，fatherpre为pre的父结点 
    BSTree p,fatherp,pre,fatherpre;
    p = T;
    fatherp=NULL;
    while (p) {//寻找被删除的节点
        if (k == p->data )break;//找到被删除的节点，退出 
        fatherp = p;
        if (k < p->data ) {
            p = p->Lchild;//在左子树中查找 
        }
        else {
            p = p->Rchild;//在右子树中查找 
        }
    }
    if (p == NULL)return T;//没有找到
    if (p->Lchild == NULL) {//p无左子树时
        if (fatherp== NULL) {
            T = p->Rchild;//p为根，删除后，其右子为根 
        }
        else if (fatherp->Lchild == p) {//p为q的左子树时，将p的右子树给q的左子树 
            fatherp->Lchild = p->Rchild;
        }
        else {//p为q的右子树时，将p的右子树给q的右子树 
            fatherp->Rchild = p->Rchild;
        }
        free(p);
    }
    else {//当p的左子树存在时，寻找p在中序的直接前驱pre
        fatherpre = p;
        pre = p->Lchild;
        while (pre->Rchild) {
            fatherpre = pre;
            pre = pre->Rchild;
        }
        p->data = pre->data;//以pre节点代替p结点，相当于删除p结点
        if (fatherpre!= p) {
            fatherpre->Rchild = pre->Lchild;
        }
        else {
            fatherpre->Lchild = pre->Lchild;
        }
        free(pre);
    }
    return T;
}

查找效率分析

在查找运算中，需要对比关键字的次数称为查找长度

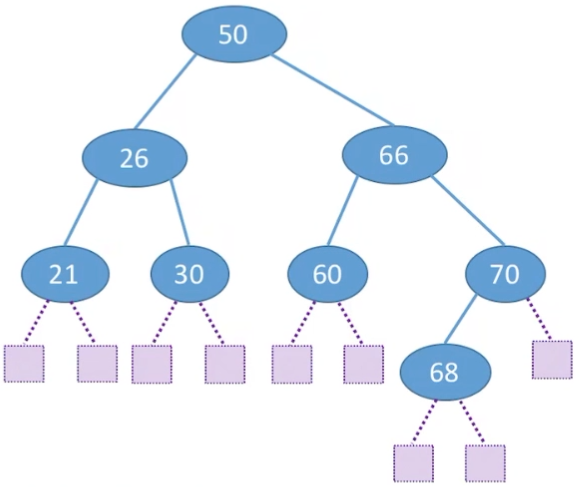
image-20220512143616816

查找失败的平均查找长度ASL=(3×7+4×2)/9=3.22

因为没有要求BST平衡，所以查找和插入的时间复杂度在O(n)（最坏情况下形成单枝树)

平衡二叉树（AVL）

平衡二叉树，首先是二叉排序树，然后树上任一结点的左子树和右子树的高度之差不超过1

平衡因子：左子树高-右子树高

平衡二叉树的平衡因子只有可能是-1,0,1

定义

1
2
3
4
5
6
//定义二叉排序树
typedef struct BSTNode {
    ElemType data;
    int bf;//balance flag
    struct BSTNode* lchild, * rchild;
}*BSTree, BSTNode;

让AVL维持平衡是重点，根据不同的插入位置，AVL维持平衡的方法也有不同

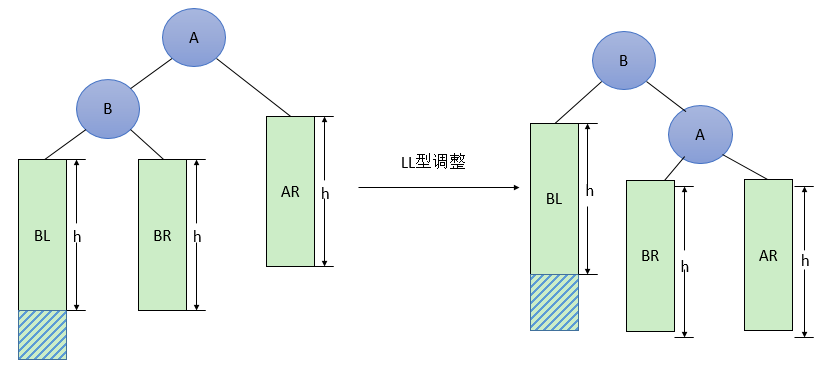
  1. LL型

    即在AVL的左孩子的左子树上插入了新节点

    调整方法：①将A的左孩子B提升为新的根结点；②将原来的根结点A降为B的右孩子；③各子树按大小关系连接(BL和AR不变，BR调整为A的左子树)

    image-20220512135105861

    代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    // 右旋操作
    void R_Rotate(BSTNode *p)   
    {
        //结合图中理解，P是结点A，而lc是结点B
        BSTree lc = p->lchild;   //定义为根节点的左孩子
        p->lchild = lc->gtrchild;   //此时lc的右孩子是null，也就是将A与B断开
        lc->rchild = p;            //让B的右孩子为A
        p = lc;                   //让B取代A成为根节点
    }-

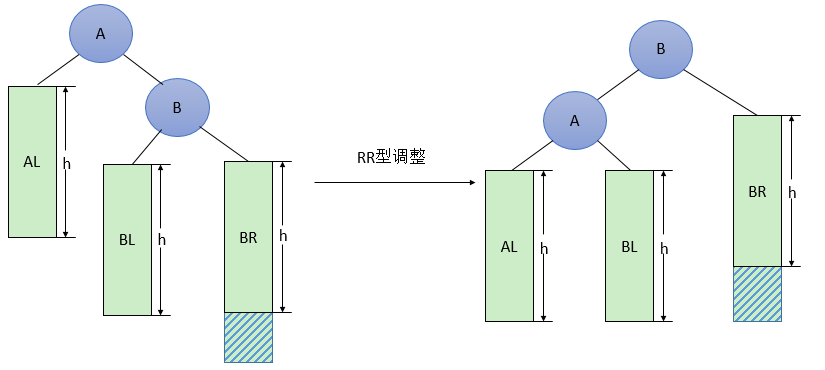
  2. RR型

    即在AVL的右孩子的右子树上插入了新节点

    调整方法：①将A的右孩子B提升为新的根结点；②将原来的根结点A降为B的左孩子；③各子树按大小关系连接(AL和BR不变，AR调整为A的右子树)

    image-20220512141059711

    代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    // 左旋操作
    void L_Rotate(BSTNode *p)   
    {
        //结合图中理解，P是结点A，而lc是结点B
        BSTree rc = p->rchild;   //定义为根节点的右孩子
        p->rchild = rc->lchild;   //此时lc的左孩子是null，也就是将A与B断开
        lc->lchild = p;            //让B的左孩子为A
        p = rc;                   //让B取代A成为根节点
    }

  3. LR型

    即在AVL的左孩子的右子树上插入了结点，导致不平衡

    ①将B的左孩子C提升为新的根结点；②将原来的根结点A降为C的右孩子；③各子树按大小关系连接(BL和AR不变，CL和CR分别调整为B的右子树和A的左子树)

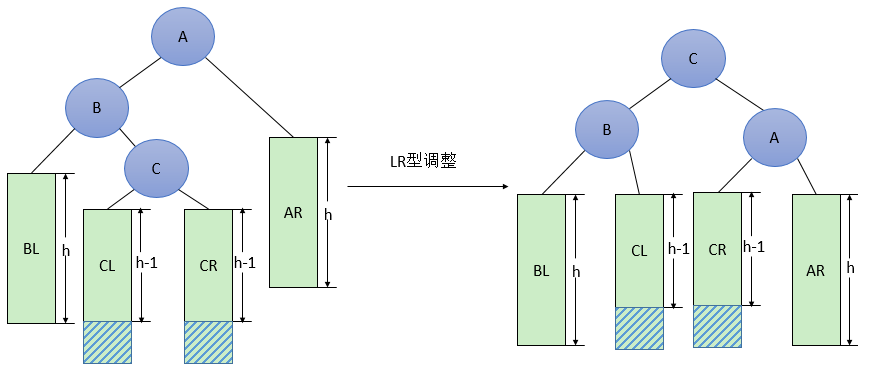
    image-20220512141340932

    代码

    1
    2
    3
    4
    5
    6
    7
    //先对B子树做左旋处理，再对A子树做右旋处理
    void LR_Rotate(BSTNode *p)
    {
     BSTree lc = p->lchild;   //定义为根结点的左孩子
     p->lchild=L_Rotate(lc);   // 将根节点的左子树左旋
     p=R_Rotate(p);           //整个根节点右旋
    }

  4. RL型

    即在AVL的右孩子的左子树上插入了结点，导致不平衡

    ①将B的左孩子C提升为新的根结点；②将原来的根结点A降为C的左孩子；③各子树按大小关系连接(AL和BR不变，CL和CR分别调整为A的右子树和B的左子树)

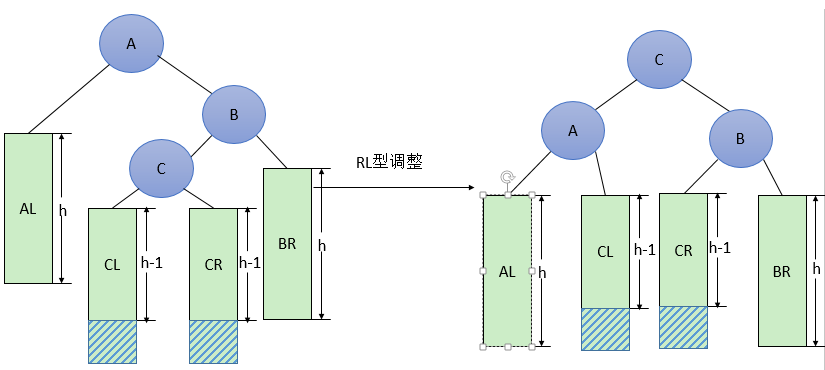
    image-20220512142406409

    代码

    1
    2
    3
    4
    5
    6
    7
    //先对B子树做右旋处理，再对A子树做左旋处理
    void RL_Rotate(BSTNode *p)
    {
     BSTree rc = p->rchild;   //定义为根结点的右孩子
     p->rchild=R_Rotate(rc);   // 将根节点的右子树右旋
     p=L_Rotate(p);           //整个根节点左旋
    }

    不平衡的子树就是需要进行操作树，如果整体不平衡，那就调整整体，总之：RR，LL是下一个当父节点，而RL和LR是跳一个当父节点，C的孩子结点是之前的父节点

求二叉树的平衡因子,即分别求树左子树和右子树的深度，相减即是平衡因子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int Factor_Depth_Make(Tree T)
{
    if(T)
    {
        int left,right;
		left=right=0;
		if(T->llink)
			left=Factor_Depth_Make(T->llink);
        if(T->rlink)
			right=Factor_Depth_Make(T->rlink);
        T->bf=left-right;
        T->depth+=(left>right?left:right);
        
        return T->depth;
    }
}

查找的时间复杂度不可能超过$O(h)$,平均查找长度为$O(log_2n)$

n层的平衡二叉树，节点数目最少是$F(n)=F(n-1)+F(n-2)+1$

红黑树

image-20220524153449378

AVL虽然相较于BST的查找效率有所提升，但是对AVL的操作需要频繁调整树的形态，计算平衡因子，找到最小不平衡子树，再进行旋转操作

红黑树牺牲了平衡性，换来的是不需要频繁调整树的形态，在适用于频繁插入，删除的场景，实用性更强，如果单论查找，AVL更好

1
2
3
4
5
6
7
struct Rbnode{
int key;
Rbnode *paraent;  //父节点指针
Rbnode *lchild;   
Rbnode* rchild;
int color;       //结点颜色
}

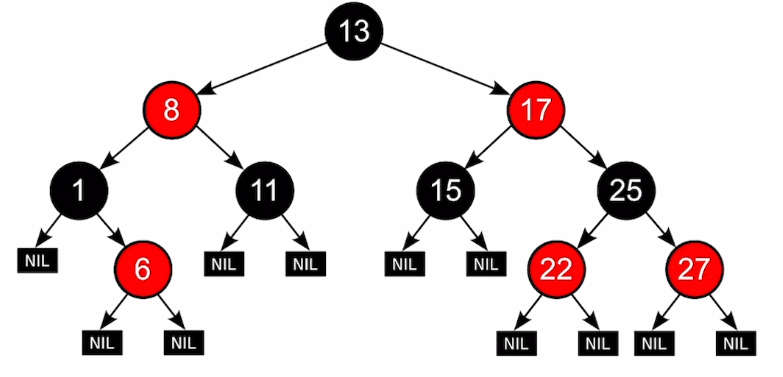
image-20220524155152233

性质：

  1. 每个结点是红色的或者黑色的
  2. 根结点是黑色的
  3. 每个叶结点(NIL)是黑色的
  4. 不存在两个相邻的红结点
  5. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
  6. 新加入的结点是红色结点

推论：

  1. 从根节点到叶子节点的最长路径不大于最短路径的2倍，当红色节点和黑色节点数量相同时，就是最长路径，也就是黑色节点（或红色节点）* 2
  2. 有n个内部结点的红黑树高度$h<2log_2(n+1)$

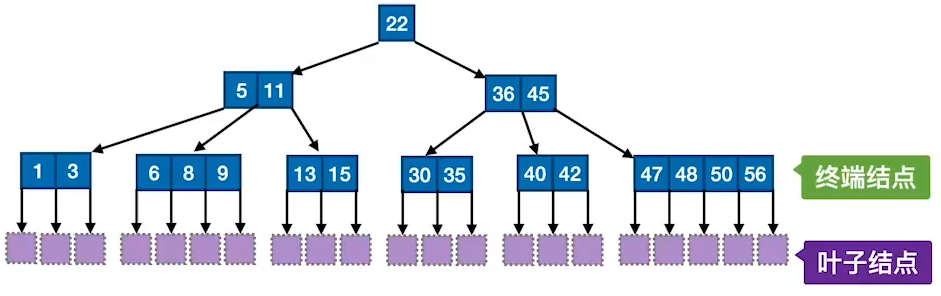
B树

又称多路平衡查找树，B树中所有结点的孩子的个数的最大值称为B树的阶，通常用m表示，一棵m阶B树应满足以下性质：

B树就是m叉平衡排序树

  1. 树中每个结点至多有m棵子树，即至多有m-1个关键字
  2. 若根节点不是终端结点，则至少有两棵子树
  3. 除根节点外的所有非叶结点至少有[m/2]（向上取整）棵子树，即至少有[m/2]-1个关键字
  4. 所有叶节点出现在同一层次上，并不带信息，叶子结点不算入树的高度

image-20220524162027943

1
2
3
4
5
struct Node{
    ElemType keys[4]; //4个关键字
    struct Node *child[5];  //5个孩子
    int num;
}

B树：为磁盘而生

传统用来搜索的平衡二叉树有很多，如 AVL 树，红黑树等。这些树在一般情况下查询性能非常好，但当数据非常大的时候它们就无能为力了。原因当数据量非常大时，内存不够用，大部分数据只能存放在磁盘上，只有需要的数据才加载到内存中。一般而言内存访问的时间约为 50 ns，而磁盘在 10 ms 左右。速度相差了近 5 个数量级，磁盘读取时间远远超过了数据在内存中比较的时间。这说明程序大部分时间会阻塞在磁盘 IO 上。那么我们如何提高程序性能？减少磁盘 IO 次数，像 AVL 树，红黑树这类平衡二叉树从设计上无法“迎合”磁盘

平衡二叉树是通过旋转来保持平衡的，而旋转是对整棵树的操作，若部分加载到内存中则无法完成旋转操作。其次平衡二叉树的高度相对较大为$log_2n$，这样逻辑上很近的节点实际可能非常远，无法很好的利用磁盘预读（局部性原理），所以这类平衡二叉树在数据库和文件系统上的选择就被 pass 了

B树多叉的好处非常明显，有效的降低了B-树的高度，为底数很大的$logn$，底数大小与节点的子节点数目有关，一般一棵B-树的高度在 3 层左右。层数低，每个节点区确定的范围更精确，范围缩小的速度越快（比二叉树深层次的搜索肯定快很多）

含有n个非叶子结点的m阶B树中总共至少包含$(n-1)([m/2]-1)+1$个关键字，因为非叶子结点至少有$[m/2]-1$个关键字，而根节点最少有1个关键字

插入操作

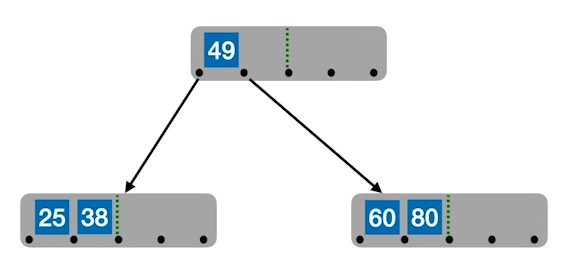
image-20220524163844052

一定是插入到底层结点，如果插入key后导致原结点关键字数超过上限，则从中间位置$[m/2]$，将其中关键字分为两部分，左部分包含关键字放在原结点中，右部分包含关键字放在新结点中，而中间位置$[m/2]$插入原结点的父节点

删除操作

若被删除的关键字在非终端节点，则用直接前驱或直接后继来替代被删除的关键字

若被删关键字在终端结点，

  1. 被删关键字所在结点中的关键字数目不小于⌈m/2⌉，则只需从该结点删除该关键字
  2. 被删关键字所在结点中的关键字数目等于⌈m/2⌉-1，而与该结点相邻的右兄弟结点（或者左兄弟）结点中的关键字数目大于⌈m/2⌉-1，只需将该兄弟结点中的最小（或者最大）的关键字上移到双亲结点中，然后将双亲结点中小于（或者大于）且紧靠该上移关键字的关键字移动到被删关键字所在的结点中。(兄弟上去，双亲下来)
  3. 被删除关键字所在的结点如果和其相邻的兄弟结点中的关键字数目都正好等于⌈m/2⌉-1，假设其有右兄弟结点，且其右兄弟结点是由双亲结点中的指针 Ai 所指，则需要在删除该关键字的同时，将剩余的关键字和指针连同双亲结点中的 Ki 一起合并到右兄弟结点中。（双亲和兄弟合并）

B+树

B+树是B-树的变体，也是一种多路搜索树, 它与 B- 树的不同之处在于:

  1. 所有关键字存储在叶子节点出现,内部节点(非叶子节点并不存储真正的 data)
  2. 为所有叶子结点增加了一个链指针

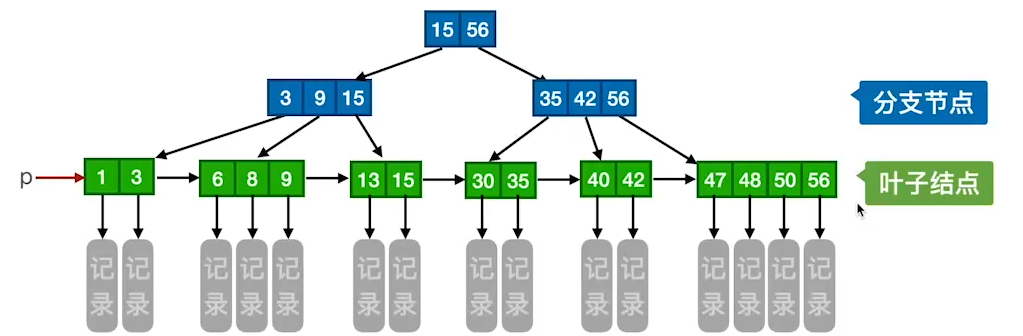
image-20220524164949895

所有叶节点包含全部关键字以及指向相应记录的指针，并且相邻叶节点按大小顺序相互链接起来，支持顺序查找

和B树的不同之处在于：

  1. B+树内节点不存储数据，所有 data 存储在叶节点导致查询时间复杂度固定为 log n。而B-树查询时间复杂度不固定，与 key 在树中的位置有关，最好为O(1)。
  2. B+树叶节点两两相连可大大增加区间访问性，可使用在范围查询等，而B-树每个节点 key 和 data 在一起，则无法区间查找。
  3. B+树更适合外部存储。由于内节点无 data 域，每个节点能索引的范围更大更精确

image-20220524165633725

散列查找

散列表(Hash Table)：又称哈希表，是一种数据结构，特点是数据元素的关键字和存储地址直接相关

用空间换时间，所以时间复杂度为O(1)

通过散列函数建立关键字和存储地址的联系

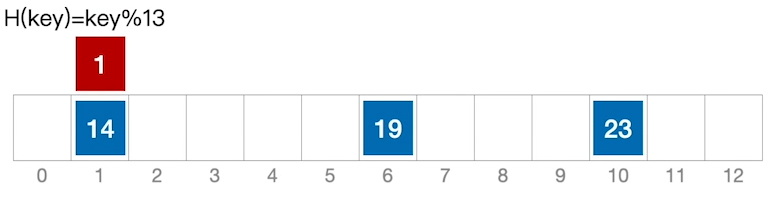
image-20220524193048839

常见的散列函数有：

  1. 除留余数法

    $H(key)=key\%b$ 取一个不大于m但最接近或等于m的质数p

  2. 直接定址法

    $H(key)=a×key+b$

    a和b是常数，适合关键字的分布基本连续的情况

  3. 数字分析法

    设关键字是r进制数，而r个数码在各位上出现的频率不一定相同，可能在某些位上分布更加均匀，可以选取更加均匀地若干位作为散列地址

  4. 平方取中法

    取关键字的平方值的中间几位作为散列地址，这种方法的散列地址与关键字的每位都有关系

如果不同的关键字通过散列函数映射到同一个值，则称位同义词，通过散列函数确定的位置已经存放了其他元素，则称这种情况为冲突

处理这种冲突有多种方法：

  1. 链地址法

    把所有同义词存储在一个链表中

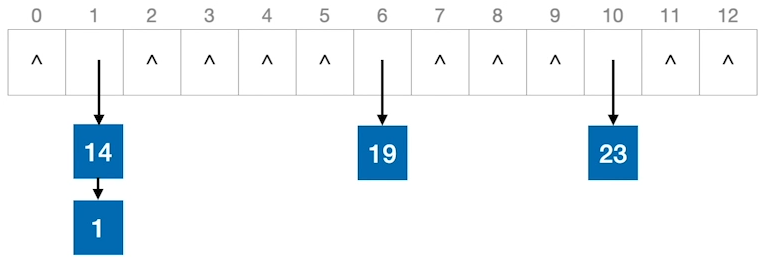
    image-20220524193148870

    装填因子$\alpha$=表中记录数/散列表长度

  2. 开放定址法

    就是可存放的空闲地址既向同义词表项开放，又向非同义词表项开放

    而线性探测法，就是当发生冲突时，就将表项往后移动一个单位即可，对散列表的查找

    如果查找到空位置则查找失败，对空位置的判断也要算作是一次比较

    image-20220524201123667

    散列函数为key%7

    $ASL_{成功}=(1+1+1+1+1+1+1+2)/8=1.125$

    因为H(key)肯定是在0~6之间的，所以只用考虑在这区间内的查找失败情况

    $ASL_{失败}=(9+8+7+6+5+4+3)/7=6$

采用开放定址法，删除结点不能简单地将被删结点置空，而是应该做一个标志，方便继续向后查找

线性探测法很容易造成同义词和非同义词的堆积，影响查找效率