6.图
图
逻辑结构
定义
图是由顶点的有穷非空集合和顶点之间边的集合组成, 通常表示为: G(V,E), 其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合
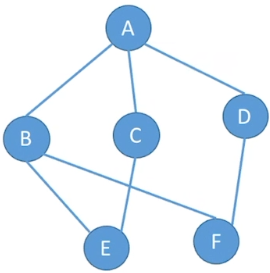
线性表可以是空表,树可以是空树,但是图不可以是空,即V一定是非空集
类型
无向图:如果E是由无向边的有限集合时,则图G为无向图
度:对于无向图,顶点的度指依附于该顶点的边的条数
无向完全图:在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有$\frac{n(n+1)}{2}$条边
有向图:若E是有向边(弧)的有限集合时,则图G为有向图,弧是顶点的有序对,记为
入度,出度:对于有向图,入度是以顶点为终点的有向边的数目,记为ID(v),出度是以顶点为起点的有向边的数目,记为OD(v),顶点的度等于其入度和出度之和,对于有向图,图的总入度和总出度肯定是相同的
有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n× (n-1)条边
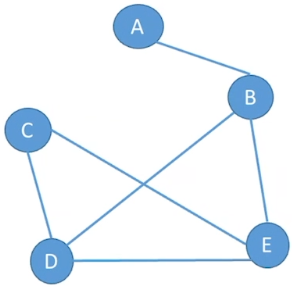
子图: 假设有两个图G= (V,{E})和G'= (V',{E'}),如果V’是V的子集,且E’是E的子集,则称G’为G的子图。如下图带底纹的图均为左侧无向图与有向图的子图。
路径和路径的长度:从顶点A到顶点B的路径是一个顶点序列。路径的长度是路径上的边或弧的数目。有向图的路径也是有向的
回路:第一个顶点和最后一个顶点相同的路径称为回路
简单路径、简单回路或简单环:序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路,称为简单回路或简单环
点与点的距离:从顶点u出发到顶点v的最短路径若存在,则此路径的长度称为从u到v的距离,若不存在路径,则记该距离为无穷($\infty$)
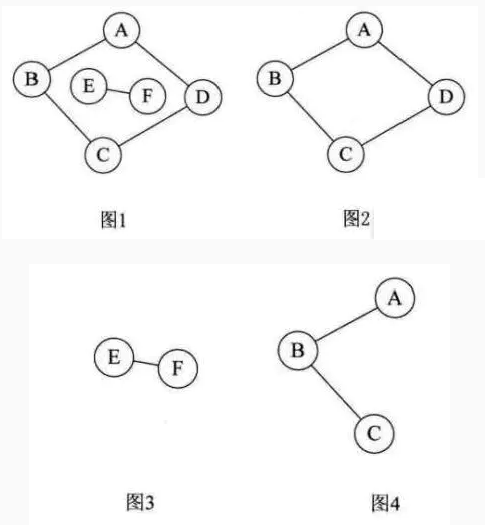
连通、连通图和连通分量:在无向图G中,如果从顶点v到顶点v’有路径,则称v和v’是连通的。 如果对于图中任意两个顶点vi、vj ∈E, vi,和vj都是连通的,则称G是连通图
无向图中的极大连通子图称为连通分量。注意连通分量的概念,它强调:
- 要是子图;
- 子图要是连通的;
- 连通子图含有极大顶点数;
- 具有极大顶点数的连通子图包含依附于这些顶点的所有边。
图2,图3,图4都是无向图1的子图,图2是极大连通子图,图3也极大连通子图,图4不满足极大的特点
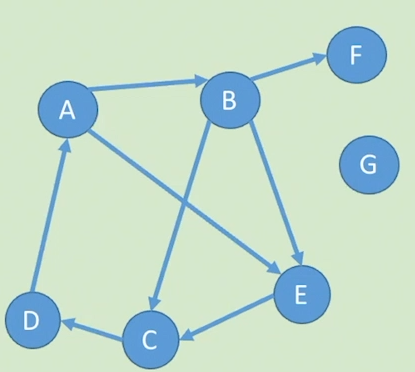
强连通图和强连通分量:在有向图G中,如果对于每一对vi,vj属于E,从vi到vj和vj 到vi都有路径,则称G是强连通图。有向图中的极大强连通子图称作有向图的强连通分量。
即ABCDE组成了一个强连通分量,而F缺乏到B的路径,没有包含在内,F和G单独为一个强连通分量
每一个孤立结点都构成连通分量
生成树:一个极小的连通子图, 它含有图中全部的n个顶点,但只有足以构成一棵树的n-1条边,简而言之就是用最少的边连接所有顶点
权和网:有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫做权。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网
树是一种不存在回路,且连通的无向图
性质
无向图边数的2倍等于各顶点的度数的总和
存储结构
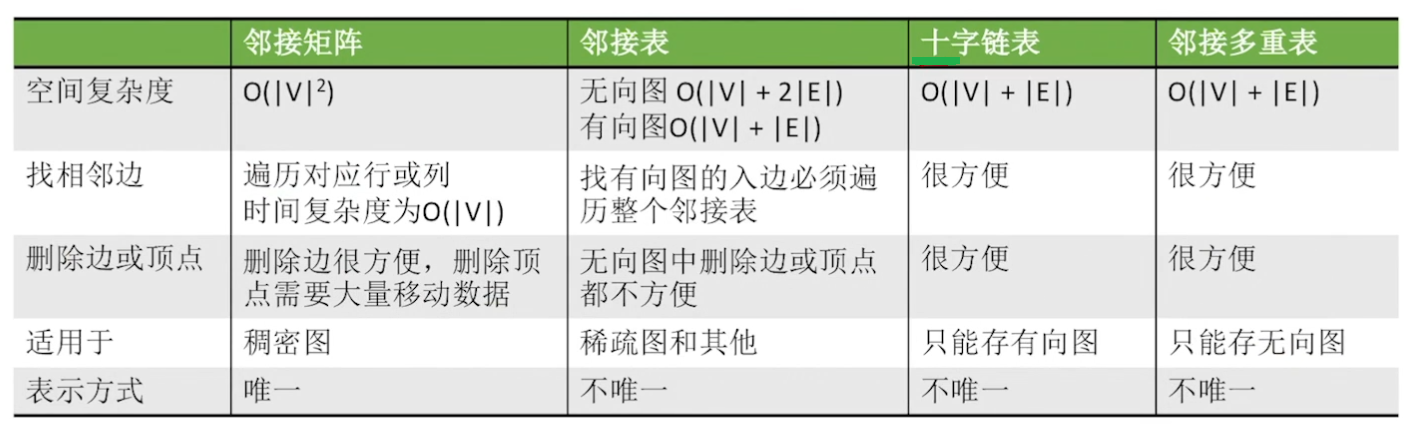
邻接矩阵法
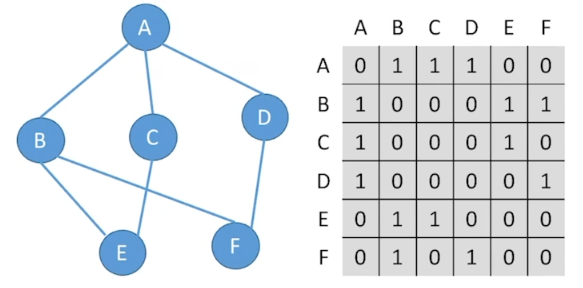
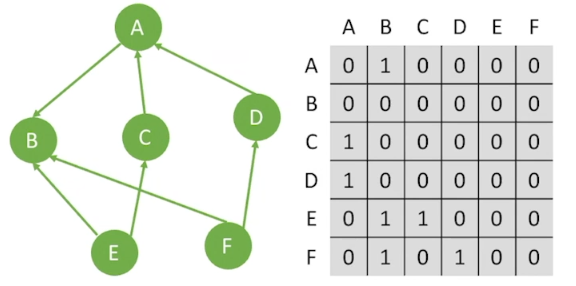
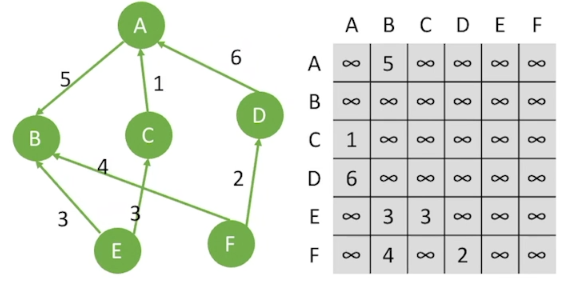
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息
定义
1 |
|
1 | //查找元素v在一维数组 Vertex[] 中的下标,并返回下标 |
结点数为n的图G中,邻接矩阵是n×n大小的,初始化数值为0,如果i行j列数值为1,表示第i个元素到第j个元素存在路径,在无向图中,是双向的,即i行j列以及j行i列数值都会为1,而在有向图中,是单向的
无向图:
有向图:
创建邻接矩阵
1 | //无向图和有向图 |
对于带权图(网)来说,将矩阵里面的值初始化为∞,如果存在路径,则路径的值为权值
无向网:
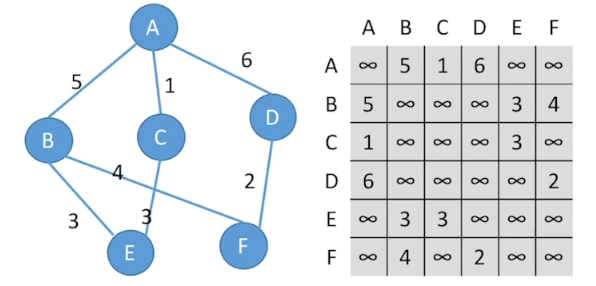
有向网:
对有向图来说
第i个结点的出度=第i行非零元素个数
第i个结点的入度=第i列非零元素个数
第i个结点的度=第i行,第i列非零元素个数之和
邻接矩阵法求顶点的度的时间复杂度为O(n),空间复杂度为O(n²),之和顶点数有关,和实际边数无关,适用用于存储稠密图,而且无向图的邻接矩阵是对称矩阵,可以压缩存储
设图G的邻接矩阵为A,则$A^n$的元素$A^n[i][j]$等于由顶点i到顶点j的长度为n的路径的数目
邻接表法
邻接表由顶点表和边表组成,顶点表是结构体数组,边表是一环一环的链节
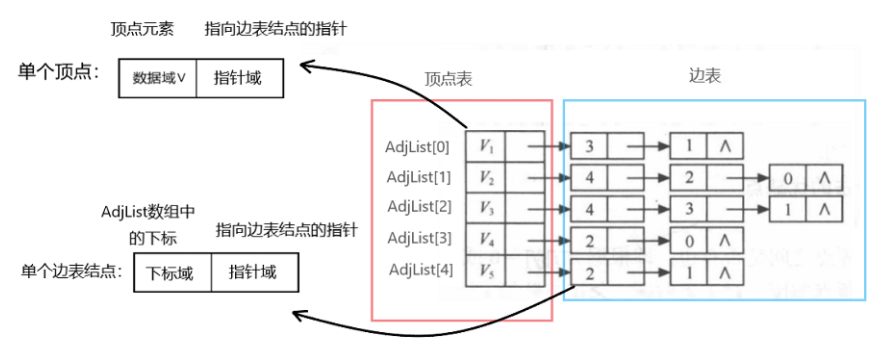
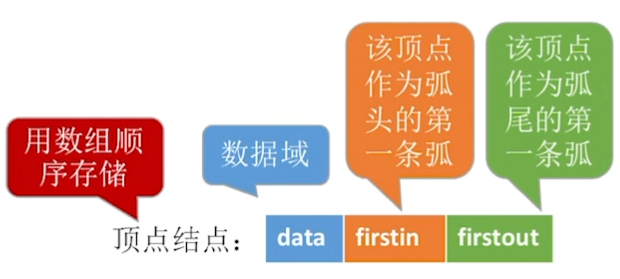
顶点表是结构体数组,其中的每个元素有两个域:
数据域(用于存放顶点元素如V1、V2、V3或A、B、C之类的)
指针域,用于连接边表。
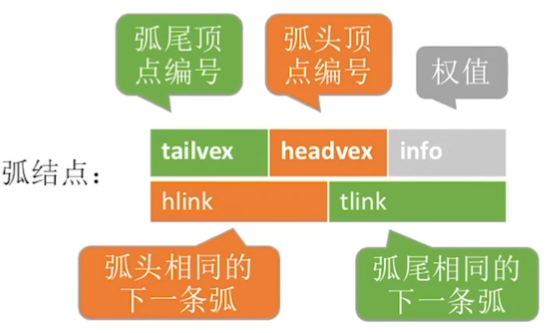
边表是结构体,其中每个结点也有两个域:
- 下标域,存储的是对应元素在顶点表中的下标。
- 指针域,用于连接后续结点
邻接表法和树的孩子表示法一模一样,都是顺序+链式存储
定义
1 | typedef struct ArcNode//边表 |

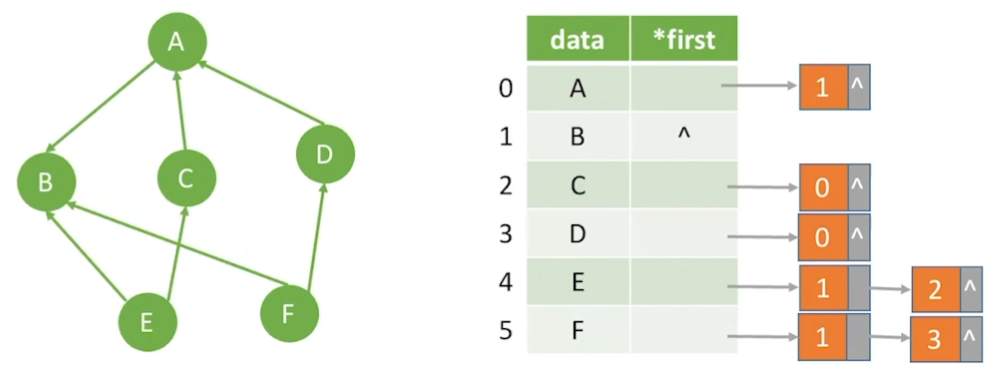
对于无向图,边节点的数量是2n,整体空间复杂度为V+2n
对于有向图,边节点的数量是n,整体空间复杂度为V+n
在无向图中,如果要求节点的度,遍历节点的边表即可,在有向图中,如果要找有向边的入度,那么需要遍历所有结点
图的邻接表表示并不唯一,空间复杂度低,适合存放稀疏图
邻接多重表
因为邻接表法在存储无向图的时候会存储冗余数据,所以利用十字链表的方法,使用邻接多重表来存储无向图
比起十字链表法,邻接多重表只有边表被扩充了
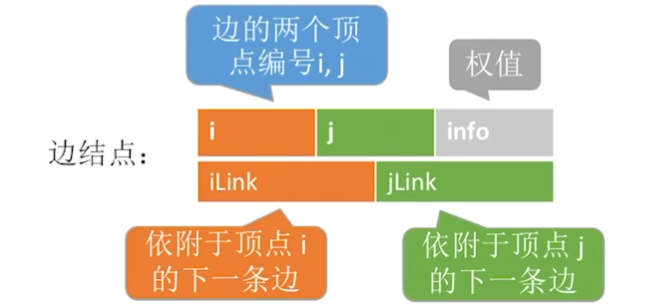
空间复杂度V+n,而且删除边和节点操作变得简单,只适合用存储无向图
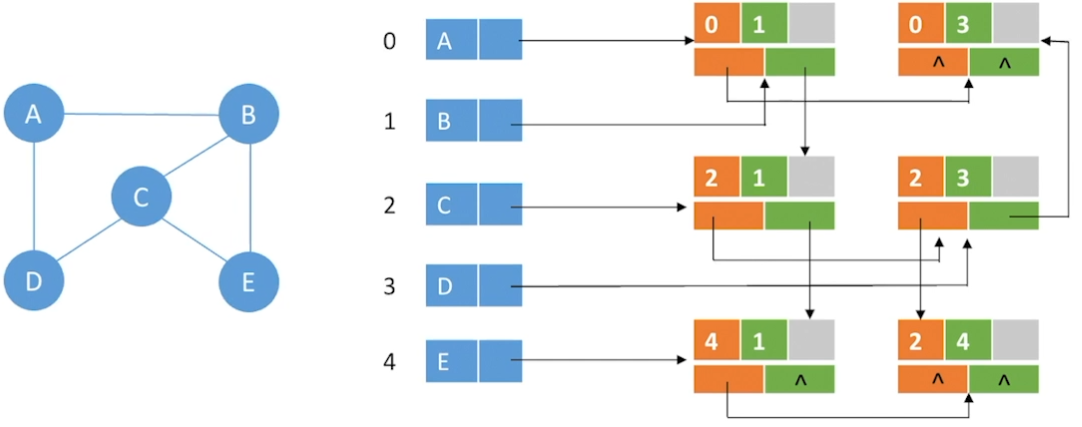
十字链表法
邻接表法容易求顶点的出度,但不容易求顶点的入度
如果我们更改邻接表的定义,将有向图中指向该结点的弧记录为孩子,那么就变成了逆邻接表,容易求顶点的入度,但不容易求顶点的出度
如果把邻接表和逆邻接表结合起来,既可以方便求入度,也可以方便求出度,这就是十字链表法
顶点结点:
弧结点:
相比于邻接表法,顶点表多了一个firstin区域,用于记录指向结点的弧
边表扩充了一倍,同时记录了弧头顶点编号和弧头相同的下一条弧(橙色部分)
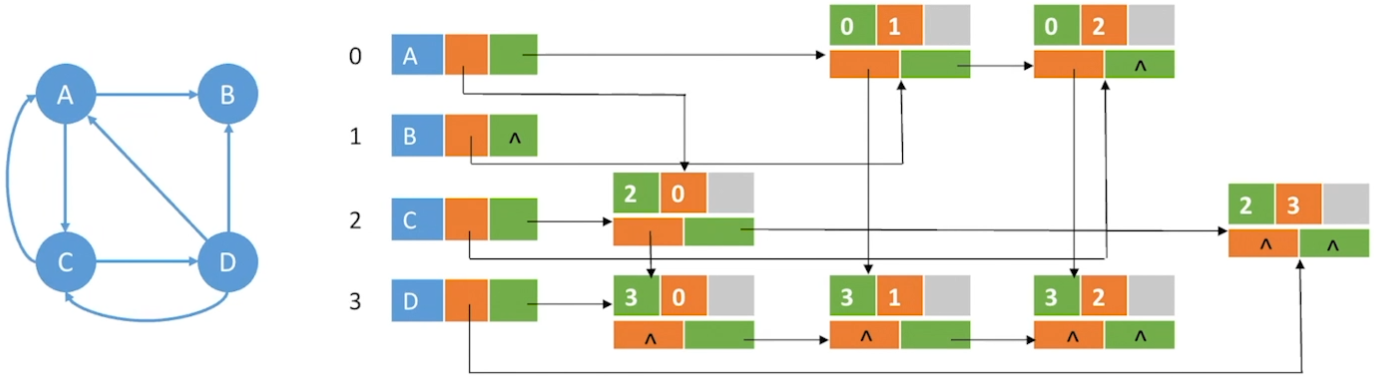
(如果把橙色区域以及指针全去了,就是邻接表法)
空间复杂度为V+n,只适合存储有向图
遍历
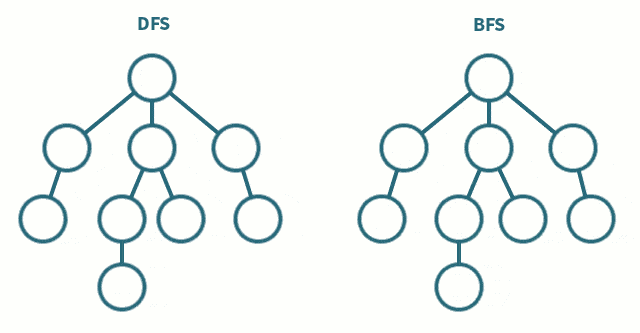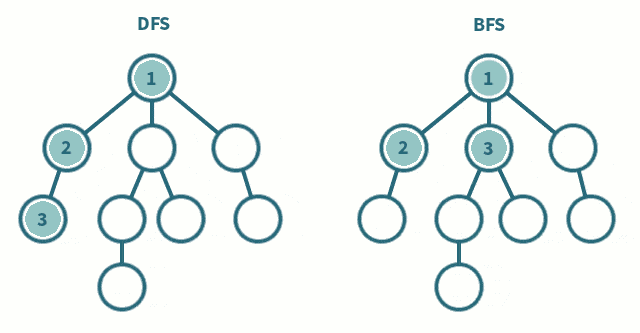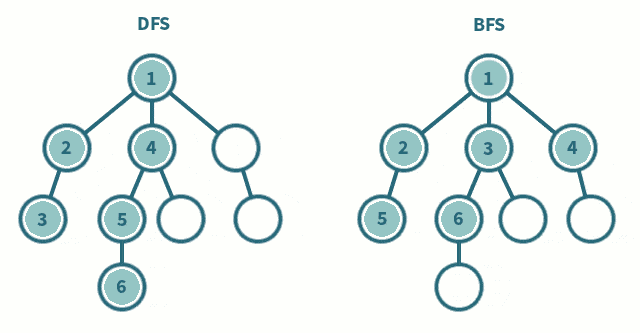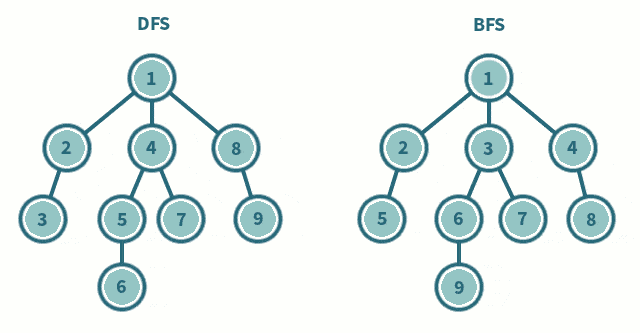
广度优先遍历(BFS)
类似于树的层次遍历
即先从某个结点开始,先遍历最离其最近的结点,再遍历到深层的结点
基本步骤:
设置全局变量
visited数组并初始化为全0,代表所有节点均未被访问设置起始点:包括对起始点进行输出、标记成已访问、入队
对后续结点进行操作:由起始点开始,对后续结点进行操作(输出、标记成已访问、入队)
(步骤2-3为广度优先搜索)循环重复2-3的操作避免有“孤岛”结点被遗漏。
(步骤4 循环执行广度优先搜索避免遗漏“孤岛”结点,就是广度优先遍历)
1 | //邻接矩阵法 |
对于BFS,邻接矩阵的遍历序列唯一,邻接表不唯一
对于无向图,调用BFS函数的次数等于连通分量的次数
空间复杂度:来自于辅助队列,大小为O(n)
时间复杂度:
对于邻接矩阵:针对每一个元素i,都会扫描j列来确定是否邻接,所以其时间复杂度为O(n²)
对于邻接表:针对每一个元素i,只需要找其边表即可确定邻接的点,所以时间复杂度为O(n)
深度优先遍历(DFS)
类似于树的先序遍历
基本步骤
- 设置全局变量
visited数组并初始化为全0,代表所有节点均未被访问 - 选取初始端点:对初始端点进行访问,并在
visited数值中标记成已访问状态(代码演示的初始端点是G->Vertex[i],此时i=0) - 循环对所有节点都执行步骤2,前提是该节点未被访问!(对应函数
DFSTraverse,主要用于非连通图能访问到每一个结点)
1 | int visitedDFS[VertexMax];//定义"标志"数组为全局变量 |
对于BFS,邻接矩阵的遍历序列唯一,邻接表不唯一
空间复杂度:来自于递归调用工作栈,大小为O(n)
时间复杂度:
对于邻接矩阵:针对每一个元素i,都会扫描j列来确定是否邻接,所以其时间复杂度为O(n²)
对于邻接表:针对每一个元素i,只需要找其边表即可确定邻接的点,所以时间复杂度为O(n)
最小生成树
在无向网中,所有路径的权值之和最小的生成树,称为最小生成树(Minimum Cost Spanning Tree)
普里姆算法(Prim)
对顶点操作,在最小生成树的顶点集U和待处理顶点集V-U中,不断地寻找最短边(代价最小边),找到后将对应顶点加入集合U,直到所有顶点均处理完毕(V-U里没有剩余顶点)
首先我们需要一个结构体数组:最短路径数组
shortedge来存储当前各个顶点之间的最短路径信息,其中的adjvex用于存储最短边的邻接点,lowcost是其对应权值,也就是当前最小的代价对
shortedge数组写入初始化信息,将起始点放入集合U中,即shortedge[k].lowcost=0;lowcost为0表示该顶点属于U集合,k是起始点的位置求最小值的函数(
minimal):只需要在当前shortage数组中比较出lowcost最小的元素,返回它的下标loc即可在Vertex数组中找到该元素。对后续顶点处理:通过
minimal函数找到最小路径所对应的的顶点, 将此路径对应的顶点放入集合U中(将其对应的lowcost改为0),更新shortedge数组(集合U中加入新的顶点,阵营U中有可能生成新的最小路径到达阵营V-U中)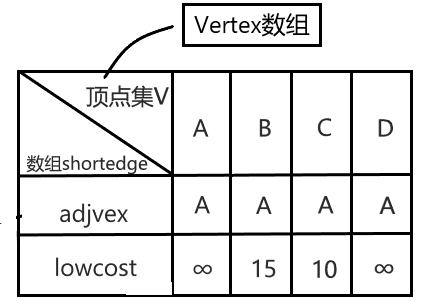
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
//1.结构体数组存储最短路径
typedef struct//最短路径数组结构体(候选最短边)
{
char adjvex;//候选最短边的邻接点
int lowcost;//候选最短边的权值
}ShortEdge;
//3. 求最小值的函数(minimal):只需要在当前shortage数组中比较出lowcost最小的元素
// 返回它的下标loc即可在Vertex数组中找到该元素。
int minimal(MGraph* G, ShortEdge* shortedge)
{
int i;
int min, loc;
min = MaxInt;
for (i = 1; i < G->vexnum; i++)
{
if (min > shortedge[i].lowcost && shortedge[i].lowcost != 0)
{
min = shortedge[i].lowcost;
loc = i;
}
}
return loc;
}
void MiniSpanTree_Prim(MGraph* G, VertexType start)
{
int i, j, k;
ShortEdge shortedge[VertexMax];
//2.处理起始点start,写入初始信息
k = LocateVex(G, start);
for (i = 0; i < G->vexnum; i++)
{
shortedge[i].adjvex = start;
shortedge[i].lowcost = G->AdjMatrix[k][i];
//G是无向网,AdjMatrix[k][i]中存的是权值
}
shortedge[k].lowcost = 0;//lowcost为0表示该顶点属于U集合
//4.处理后续结点
for (i = 0; i < G->vexnum - 1; i++)//对集合U,去找最短路径的顶点
{
k = minimal(G, shortedge);//找最短路径的顶点
printf("%c->%c,%d\n", shortedge[k].adjvex, G->Vertex[k], shortedge[k].lowcost);
//输出找到的最短路径顶,及路径权值
shortedge[k].lowcost = 0;//将找到的最短路径顶点加入集合U中
for (j = 0; j < G->vexnum; j++)
//U中加入了新的K节点,可能出现新的最短路径,故更新shortedge数组
{
if (G->AdjMatrix[k][j] < shortedge[j].lowcost)
//有更短路径出现时,将其替换进shortedge数组
{
shortedge[j].lowcost = G->AdjMatrix[k][j];
shortedge[j].adjvex = G->Vertex[k];
}
}
}
}
时间复杂度:O(n²),显然有个嵌套,第一个嵌套是遍历n-1个节点,时间复杂度是O(n),第二个嵌套中,先要找到最短路径的顶点,即miniaml函数,时间复杂度是O(n),找到后需要更新shortedge数组,时间复杂度是O(n),共O(2n),所有总时间复杂度为O(n²)
适合于稠密图
克鲁斯卡尔算法(Kruskal)
每次选取最短边,但不能构成回路
如果用邻接矩阵和邻接表,每次寻找最短边都要搜索所有边,故邻接矩阵和邻接表均不合适,所以最终选用了边集数组
边集数组edge是一个结构体数组,每一个单元包含起点、终点、权值
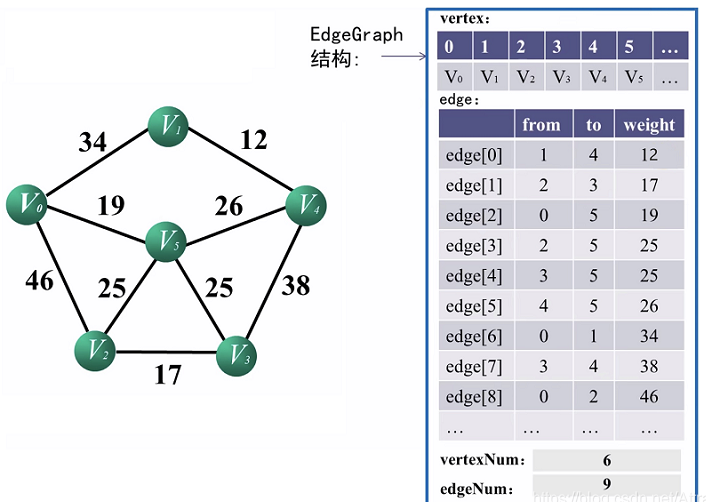
定义
1 | typedef struct |
选取最短边的关键:排序
1 | //选用简单排序 |
检查回路:只需要看两个顶点所属的树是否有相同的根节点,使用了并查集判断是否成环
1 | int FindRoot(int t,int parent[])//t接收到是结点在Vertex数组中的下标 |
完整代码
1 | void MiniSpanTree_Kruskal(EdgeGraph *E) |
排序算法决定了克鲁斯卡尔算法的时间复杂度。若采用插入排序,时间复杂度为$O(n²)$ ,若采用堆排序或者快速排序,那么时间复杂度为$O(nlog_2n)$ [注:$n$为边数],也就是说克鲁斯卡尔算法的时间复杂度取决于边数,所以适合稀疏图
最短路径问题
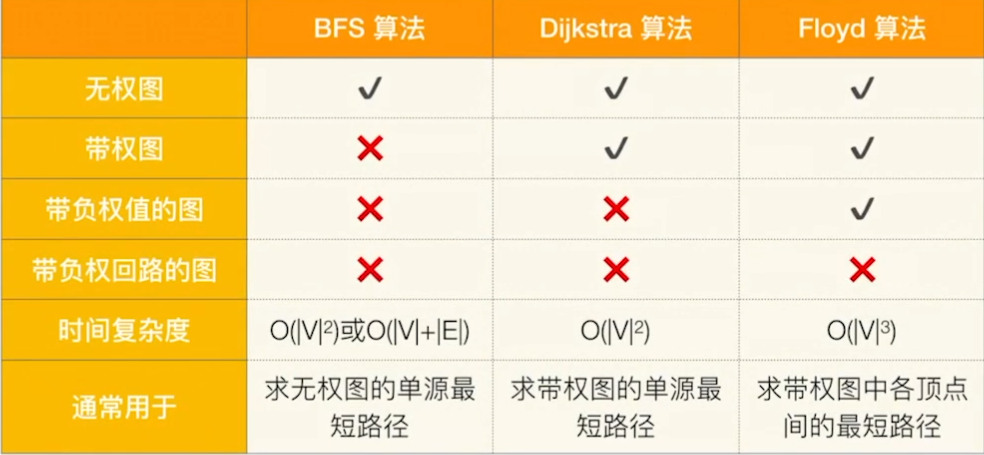
最短路径算法
- 对于网(带权图)而言,求两点之间的最短路径有两种算法:迪杰斯特拉(Dijkstra算法)和 弗洛伊德(Floyd算法)
- 单源最短路径—迪杰斯特拉算法:从一个起始点出发,到达一个终点
- 多源最短路径—弗洛伊德算法:求每一对顶点之间的最短路径
迪杰斯特拉算法(Dijkstra)
迪杰斯特拉算法处处可见普里姆算法的影子,大体上两者都是在寻找当前情况下的最短边,而不同之处在于,迪杰斯特拉算法做了路程的累加
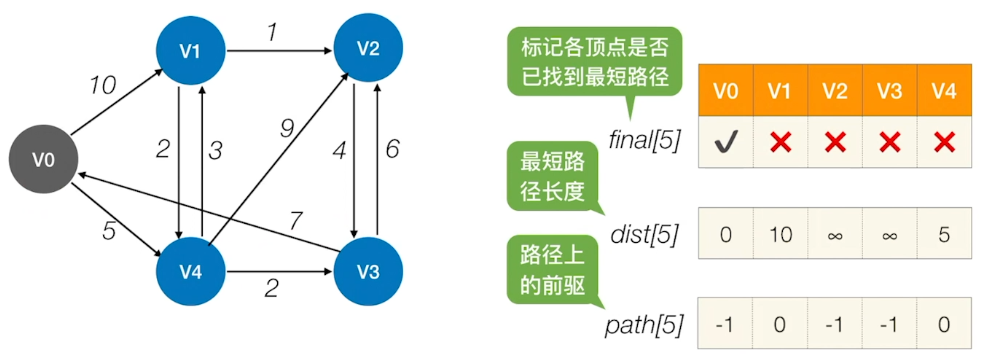
1 | int FindMinDist(int dist[],int s[],int vexnum) |
时间复杂度:O(n²)
弗洛伊德算法(Floyd)
多源点意为多起始点,也就是图中所有顶点都将作为起始点,求此顶点到达图中其他所有顶点的最短路径
在之前学习的Dijskra算法,我们知道Dijskra算法是求解单源点最短路径的算法,使用Dijskra算法可以求出一个源点到其他所有顶点的最短路径,那么我们将Dijskra算法循环执行n次(n为顶点数),每次带入图中的一个顶点,不就实现了求解多源最短路吗?
Dijskra算法执行单次的时间复杂度为$O(n^2)$,其中n为顶点个数,循环执行n次,那么使用Dijskra算法求解多源点最短路径的整体时间复杂度为$O(n^3)$
此次我们引入的求解多源点最短路径问题的算法是——Floyd算法,时间复杂度也为$O(n^3)$,但是在算法构造和算法可读性上优于执行n次的Dijskra算法
弗洛伊德的核心思想是:对于网中的任意两个顶点(例如顶点 A 到顶点 B)来说,之间的最短路径不外乎有 2 种情况:
- 直接从顶点 A 到顶点 B 的边的权值为顶点 A 到顶点 B 的最短路径。
- 从顶点 A 开始,经过若干个顶点,最终达到顶点 B,期间经过的边的权值和为顶点 A 到顶点 B 的最短路径
所以,弗洛伊德算法的核心为:对于从顶点 A 到顶点 B 的最短路径,拿出网中所有的顶点进行如下判断:Dist(A,K)+ Dist(K,B)< Dist(A,B)
其中,K 表示网中所有的顶点;Dist(A,B) 表示顶点 A 到顶点 B 的距离
也就是说,拿出所有的顶点 K,判断经过顶点 K 是否存在一条可行路径比直达的路径的权值小,如果式子成立,说明确实存在 一条权值更小的路径,此时只需要更新记录的权值和即可
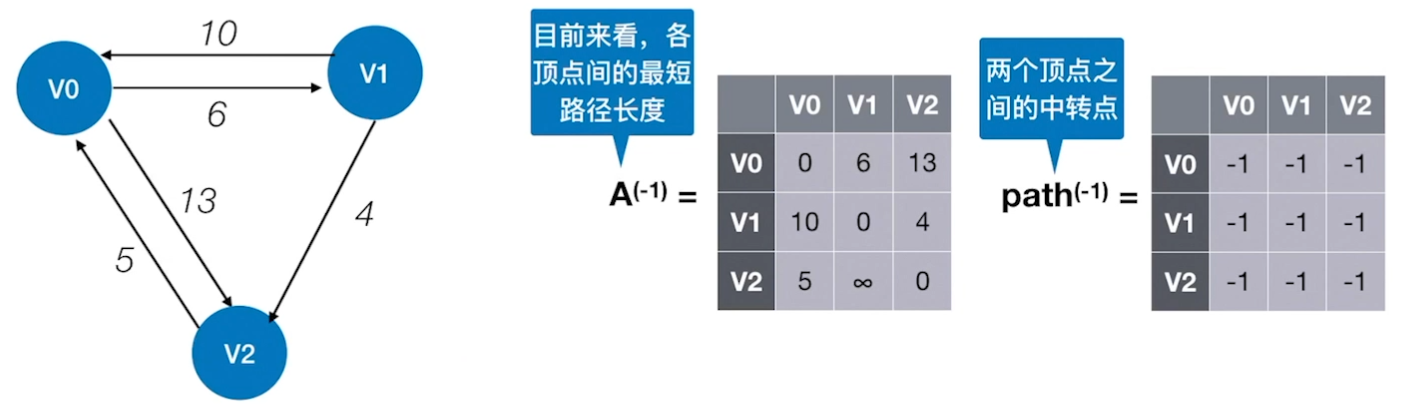
1 | int dist[VertexMax][VertexMax]; |
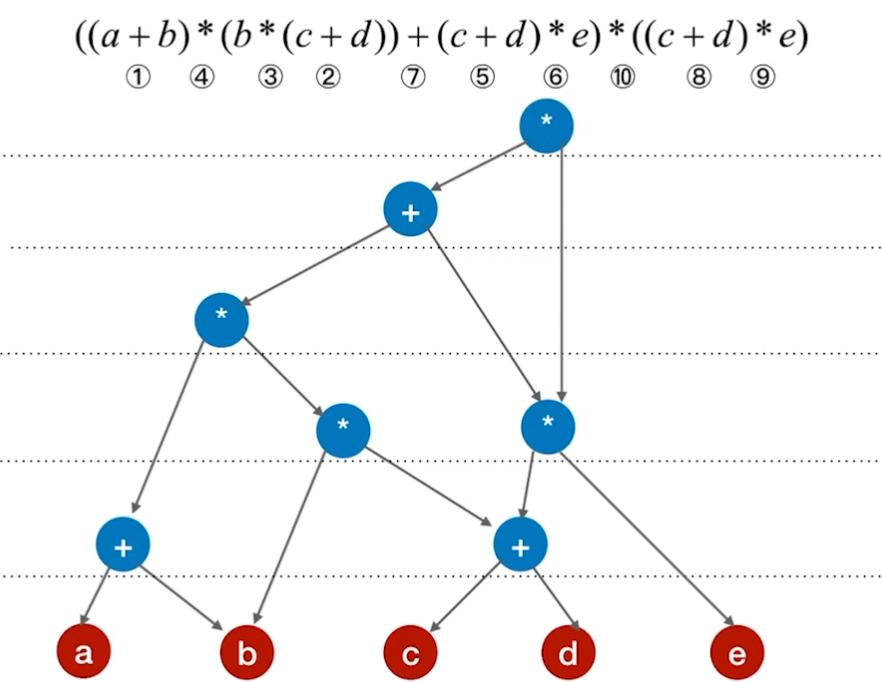
有向无环图描述表达式
- 把各个操作数不重复地排成一排
- 标出各个运算符的生效顺序
- 按顺序加入运算符,注意分层
- 从底向上逐层检查同层的运算符是否可以合体
拓扑排序
AOV网(Activity On Vertex NetWork):用顶点表示活动,边表示活动发生的 先后关系
拓扑序列:在AOV网(无环图)中,由顶点$V_i$到顶点$V_j$有一条路径,则在该线性序列中的顶点$V_i$必定在顶点$V_j$之前。
拓扑排序:将AOV网中的顶点序列排成拓扑序列就叫拓扑排序。
拓扑排序条件:必须是有向无环图(Directed Acycline Graph),AOV网满足有向无环图条件,若是有向成环图,则会进入死循环。
有向无环图只在意图中是否有环,即使不是连通图,也可以是有向无环图
拓扑排序的执行过程相当于每次 删去入度为0的顶点和这个顶点发射出去的边,那么我们每次删去一个顶点和其发射边,就会生成一个新图,在这个新图上继续执行删去入度为0的顶点和这个顶点发射出去的边,直到所有顶点都被删完。删除每个顶点的顺序,就是拓扑序列
步骤:
- 我们首先找到入度为0的顶点,然后对其进行输出,接着根据邻接表的邻接关系,找到与其邻接的其他顶点,再去对其他顶点进行相同的处理,由此往复。
- 我们需要一个 临时存取空间space,我们每次把入度为0的顶点放入space中,然后按顺序(顺序可以从头开始、从尾开始、甚至可以任意取)从space中取出,然后进行步骤1的处理,再将更新后入度为0的顶点放入space中,直到space中的元素被取空,即拓扑排序结束。
- 临时存取空间space的存取顺序可以是任意的,所以,这个space可以是栈结构,队列结构,也可以是一个数组,甚至可以是其他(源代码用数组模拟栈结构)。由此可见,存取顺序的不同,直接导致了拓扑排序结果不唯一。
- 总结一下拓扑排序在程序中的执行流程:首先我们搞了一个临时存储空间space,然后将入度为0的顶点放入space,再按顺序取出,每去取出一次,就根据邻接表的邻接关系,查找当前取出的顶点的邻接点,对每个邻接点入度-1,更新完入度后,看看有没有出现新的入度为0的结点,将其放入space中,直到space为空时,即所有顶点处理完毕,输出的序列就是拓扑序列
邻接表法:
1 | typedef struct ArcNode//边表 |
1 | int indegree[MAX];//用来存储所有节点的入度之和 |
邻接矩阵法:
1 | //邻接矩阵实现拓扑排序 |
拓扑排序可以判断图中是否存在环
逆拓扑排序:根据拓扑排序的思路,如果用逆邻接表来存储图,先输出出度为为0的结点,自然构成了逆拓扑排序
1 | void DFS(MGraph* G, int i) |
如此,DFS当然也可以用于拓扑排序,只要用队列来存储访问到的结点,就是拓扑排序
不如说,利用队列+DFS的方法是代码量最少实现拓扑排序的办法
时间复杂度:邻接表:O(V+E) 邻接矩阵:O(V²)
判断图中是否有环
DFS
思路如下,在利用DFS遍历节点时,将遍历节点的visitedDFS[i]数组设置为-1,表示正在访问,如果在之后的递归过程中发现有节点的visitedDFS[i]为-1,则表示有环
这种方法只能用于有向图,如果要用DFS检测无向图的环,需要一个parent数组记录其父节点
1 | void DFSTraverse(MGraph* G) |
拓扑排序
在上一小节中已经使用了拓扑排序来判断是否存在有向环了,而使用拓扑排序同样可以判断一个无向图中是否存在环,只要将入栈条件从度为0的结点,改成度为0或1的结点即可
并查集
并查集可以找到无向图的环,在最小生成树的克鲁斯卡尔算法(使用了边集数组)中,就已经使用了并查集来寻找图中的环
总结
无向图:
- DFS(需要数组记录父节点)
- 拓扑排序(将度为0和1的结点压入栈)
- 并查集(克鲁斯卡尔算法)
有向图:
- DFS(给visit数组多设置一个状态变量表示正在搜索)
- 拓扑排序(将度为1的结点压入栈)
关键路径
AOE网(Activity On Edge NetWork):在带权有向图中若以顶点表示事件,有向边表示活动,边上的权值表示该活动持续的时间,AOE网通常用于 估算事件/工程完成的工期(时间)
从定义上来看,很容易看出两种网的不同,AOV网的活动以顶点表示,而AOE网的活动以有向边来表示,AOV网的有向边仅仅表示活动的先后次序。纵观这两种网图,其实它们总体网络结构是一样的,仅仅是活动所表示的方式不同,因此可以猜想从AOV网转换成AOE网应该是可行的
关键路径:在AOE网中仅有一个入度为0的点,称为开始顶点,它表示整个工程的开始,也仅有一个出度为0的点,称为结束顶点,代表整个工程的结束,这两个点之间的距离有很多条,在所有路径中,具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动
所以求关键路径非常简单,只需要在图中找出权值和最大的一条或多条路即可,关键活动的最早和最晚发生时间一致,而非关键活动的最晚发生时间只需要和关键活动同时发生就行了
- 事件$v_i$的最早发生时间ve(i):事件$v_i$的最早发生时间是等待$v_i$之前的所有活动都完成,所以ve(i)是从源点到vi的最长路径长度。起始点(源点)的最早发生时间为0。($v_k$是$v_i$的前驱事件)
所以可以推出:ve(0) = 0;(源点的最早发生时间为0)i∈[1,n]时,ve(i) = Max{ ve(k) + weight(k->i)} ; - 事件$v_i$的最晚发生时间vl(i):不拖延工期的前提下,事件vi被允许的最晚发生时间。($v_k$是$v_i$的后续事件)活动ai=<$v_i$,$v_k$>,$v_i$的最晚发生时间,取决于这个活动被允许的最晚结束时间,而所被允许的最晚结束时间也正是vk的最晚开始时间,也就是vl(k),所以我们就得到等式:
最晚发生时间vl(i)+ 活动持续时间weight = 最晚结束时间vl(k)
所以可以推出:vl(n-1) = ve(n-1);(汇点的最早发生时间与最晚发生时间相等)i∈[0,n-2]时,vl(i) = Min{ vl(k) - weight(i->k)} ;
步骤:
- 求出事件最早发生时间ve[i]:顺拓扑序
- 求出事件最晚发生时间vl[i]:逆拓扑序
- 通过ve[i]和vl[i]计算出活动最早开始时间(e) 与 活动最晚开始时间(l)
- 若
e(i)==l(i)则当前i所指向的活动是关键活动(Critical Activity)
1 | void CriticalPath(ALGraph *G) |

