118.杨辉三角
118.杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
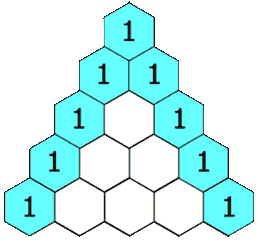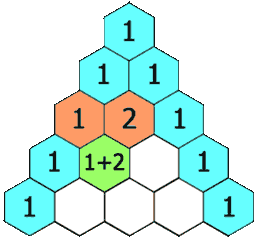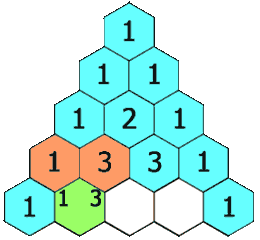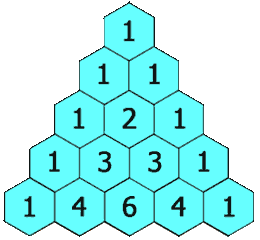
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
1 | 输入: numRows = 5 |
Solution:
每个数字等于上一行的左右两个数字之和,可用此性质写出整个杨辉三角。即第 n 行的第 i 个数等于第 n-1 行的第 i-1个数和第 i 个数之和。这也是组合数的性质之一
1 | class Solution { |
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。

1 | 输入: numRows = 5 |
Solution:
每个数字等于上一行的左右两个数字之和,可用此性质写出整个杨辉三角。即第 n 行的第 i 个数等于第 n-1 行的第 i-1个数和第 i 个数之和。这也是组合数的性质之一
1 | class Solution { |