解析：x每次都稳定翻倍，所以时间复杂度为A

解析：n每次－1，当n为1时，循环结束，所以时间复杂度为B

解析：双循环，外循环执行$log_2n$次，内循环固定执行n次，所以结果是C

解析：i的值会从1增加到n，通项求和公式为$sum=\frac{(1+n)n}{2}$，所以时间复杂度是B

解析：x以平方的速度增长，所以时间复杂度为B

解析：等差序列的求和公式了，(1+n)n/2，所以是B

解析：换个思路，从开头双指针比较，较小的元素插入到新表头，如果按头插法依次比较插入，则可以得到降序链表，显然最坏时间复杂度为max(m,n)，选D

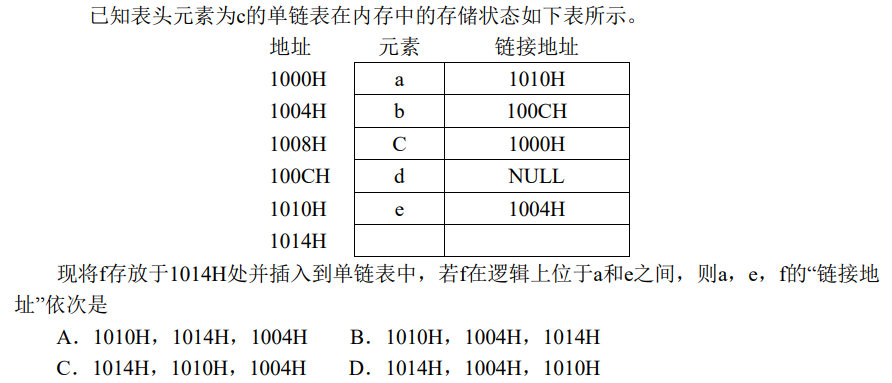
解析：根据内存表中的情况：C–a–e–b–d，如果将f插入到a，e之间，则a会连接到f，链接地址为1014H，e的链接地址不变，是1004H，f连接到e，地址为1010H，选D

解析：双向循环链表，很明显选D

解析：考虑到只有一个元素的情况，如果p=q，那么p直接指向头结点，选D

解析：行优先存储，假设每行有n个元素，那么3n+4=121，n=39，则100+39×5+6-1=300，选B

解析：对于ABC来说，要在尾结点插入一个元素都需要遍历链表，而对于循环双链表来说，只需要改变指针即可，所以选D

解析：用带尾指针的循环链表查找首尾结点的效率都是O(1)，所以选B

解析：缓冲区+先进先出 很明显是队列 选B

解析：模拟可知，栈中元素最多时为3，选C

解析：D中的f，e，d依次退栈明显违背了题目规则

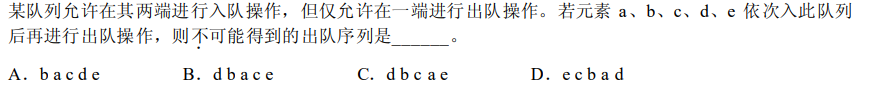
解析：以a为起点，看其左右两边是否符合规律，C明显不符合

解析：有dcbae，decba，dceba，dcbea 四种，故选B

解析：顺序表存储队列，，rear指向队尾元素，开始时rear应该为n-1，才能保证第一个元素进队后指向0，选B

解析：中缀转后缀表达式，过程中操作符最大时：-*((+，为5个，选A

解析：$p_3$不可能是3，其余皆有可能，所以选C

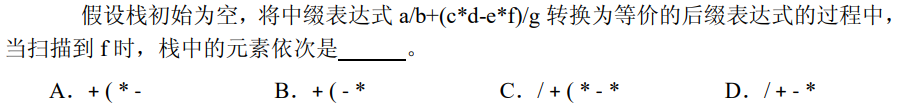
解析：中缀表达式转后缀，操作符进栈，扫描到f，栈内元素为+(-*，选B

解析：顺序表存储循环队列，首尾指针相同时队空，留一个空间以判断队满，所以选A

解析：先执行main函数，再执行S函数，选A

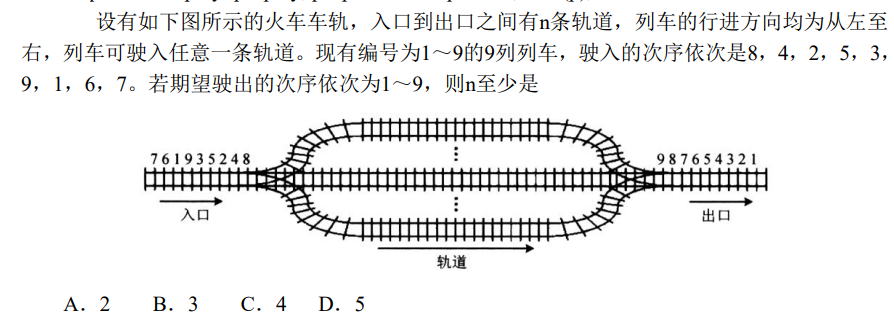
解析：这是一个栈的问题，栈结构是，栈内元素自下往上下降，8,4,2.1组成一个栈 5,3组成一个栈 ，9,6组成一个栈，7组成一个栈，最后的结果是n至少为4，选C

解析：三对角矩阵，首先，前29行的元素之和为2+28×3=86个，$m_{30,30}$是对角线元素，是第30行的第2个元素，所以是数组中的第88个元素，下标要在此基础上-1，所以答案是87，选B

解析：1，3太绝对了，2是栈的正常用途，4说法错误，所以选C

解析：三元组是存储稀疏矩阵的常规方法，而十字链表也可以存储稀疏矩阵，所以选A

解析：(8-(3+2))*5= 15，选B

解析：C的序列都是队列，但是没有按顺序

解析：上三角矩阵，前5行的元素个数是(12+8)×5÷2=50，查找元素处于第6行第6个，是对角线元素，50+1=51个元素，下标是从0开始的，所以下标是51-1=50，选A

解析：首先是对称矩阵，$m_{7,2}=m_{2,7}$，注意到是按列存放的，所以$m_{2,7}$是第1+2+3+4+5+6+2=23个，下标为个数-1=22，选C

解析：按照顺序，b，c，e，选D

解析：按照顺序，1的左右肯定有2，明显是D不合理

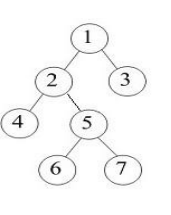
解析：很明显的RNL，选D

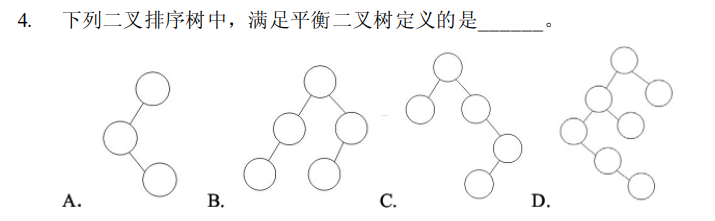
解析：根据AVL的定义，很明显的B

解析：前5层最多有$2^5-1=31$个，第6层最多有$2^{6-1}=32$个结点，其中8个叶节点，则24个非叶节点，则结点数最多为31+32+48=111个，选C

解析：首先如果v是u的左孩子的左孩子，那么肯定满足父子关系，其次如果v是u的右孩子的右孩子，则满足兄弟关系，最后，如果v是u的右孩子的左孩子，则满足u的父节点和v是兄弟关系，如果v是u的左孩子的右孩子，则u和u的父节点是兄弟关系，故3错误，选B

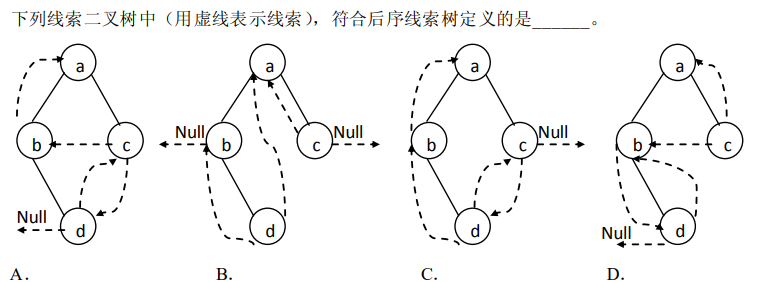
解析：符合条件的是D，后序遍历是左右根的顺序，无法找到后继

解析：插入48之后，AVL会不平衡，是RL型不平衡，即需要先右旋，再左旋，37会变成根节点，左右分别是24和53，即选C

解析：根据规律：结点数=度数+1，则n=4×20+10×3+1×2+10×1+1=123，而叶子结点数=123-20-10-1-10=82，即选B

解析：根据哈夫曼树的特点，选A

解析：完全二叉树的非叶节点=[n/2]（向下取整）=384个，即叶子结点也是384个

解析：前序序列说明根节点是1，观察选项BCD，即234都在根节点的左子树中，对34进行排序，若3,4都是左，那么D成立，若34都是右，那么B成立，无论如何C都不成立，选C

解析：极端一点，设想其2011结点的树含有116个叶子结点以及2011-116-1=1894个度为1的结点，以及一个度为116的结点，将其转化为二叉树，则有1895个结点没有兄弟，所以二叉树中也没有右孩子，再加上二叉树中最深的一个结点没有孩子，结果为1896个，选D

解析：可以确定a为根节点，而e是前序第二个以及后序倒数第二个，说明根节点只有左子树或只有右子树，则选A

解析：画出符合条件的高度为2,3的AVL，加一个根节点即是高度为4的符合条件的AVL，同理，高度为6的AVL=7+12+1=20，此题选B

解析：排序结果是一棵高度为3的完全二叉树，所以个数为3

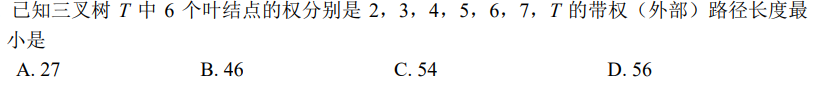
解析：6+7+(4+5)×2+(2+3)×3=46，选B

解析：右线索指向后继，是其父节点，选A

解析：如果删除的是叶节点，则最后结果是相同的，如果不是叶节点，那么结果不同，毕竟BST没有平衡机制，选C

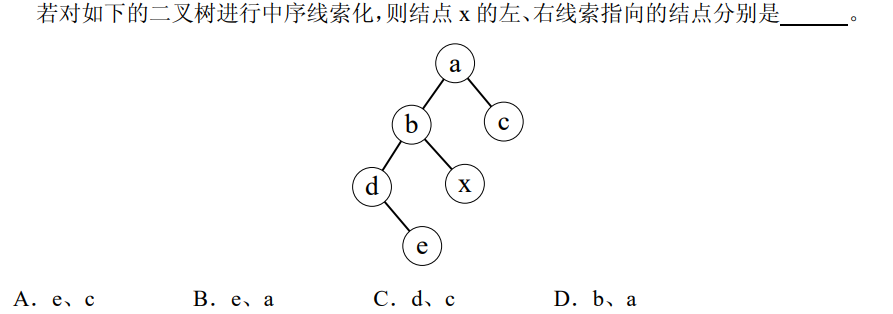
解析：中序化，x的左线索指向前驱，即是b，右线索指向后继，即是a，所以选D

解析：T中左孩子指针为空的，说明没有孩子，是叶子结点，和F中叶节点的个数相当

解析：前缀编码要求，即任一一个编码不能是其他编码的前缀，而D中，110完全是1100的前缀，所以D错误

解析：① n个不同元素进栈，出栈元素不同排列的个数为$\frac{1}{n+1}C^n_{2n}$(卡特兰数)，② 由先序序列和中序序列可以完全确定一棵二叉树 ③ 将先序序列压入栈，元素出栈的顺序构成中序序列(结合先序和中序的非递归序列来考虑，先序就是在元素入栈前访问，中序在出栈时访问) 得出结论，结果为$\frac{1}{4+1}C^4_{8}=14$ 答案选B

解析：只有CD可以结合生成24这一结点，而在C中，叶子结点10和0结合，另一边却是11和3结合，不符合哈夫曼树的定义，所以选D

解析：显然AB错误，AVL可以旋转，所以最后插入的不一定是叶节点，树中最大元素是其左子树的最左下结点，一定无左孩子，所以选D

解析：在森林中，结点数=度数+根节点数，所以是10个，选C

解析：先序序列和中序序列相同，联系到二叉树的非递归遍历，则只有右单枝树能满足条件，选B

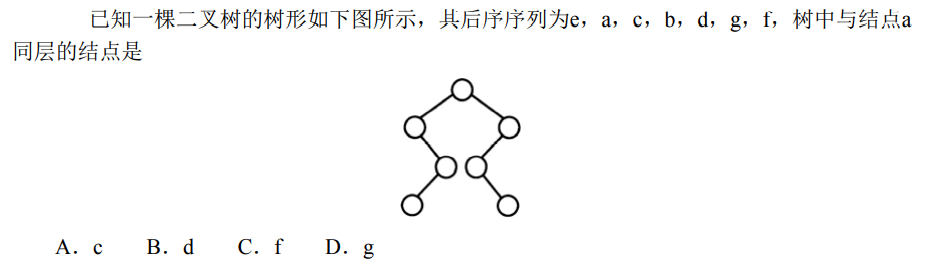
解析：在图中标记出各个结点，答案明显是B

解析：将序列解析为 0100 011 001 001 011 11 0101 所以是 a f e e f g d 所以选D

解析：是满二叉树，有k个叶节点，假设有n层，$k=2^{n-1},n=log_2k+1$，n层一共有$2^n-1$个结点，即$2k-1$个结点

解析：出现频率越高的字符，编码越短，首先排除B，D，而C不符合哈夫曼树的要求，10和1011的前缀相同了，所以选A

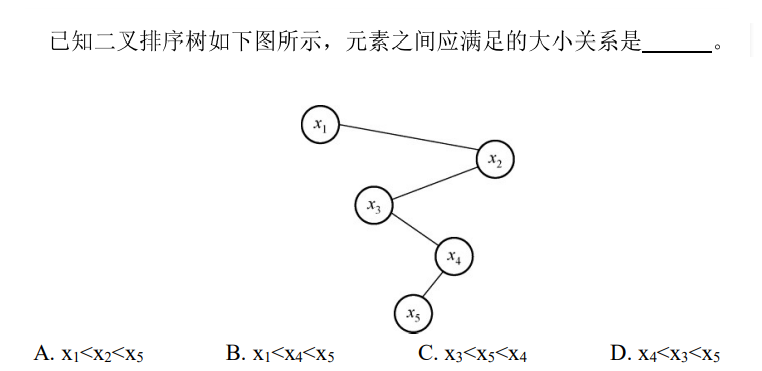
解析：BST按中序遍历顺序，依次增大或减小，所以选C

解析：概念问题，树的后根遍历=二叉树的中序遍历，选B

解析：n个哈夫曼树会新建n-1个结点，因此结点总数2n-1=115，n=58，选C

解析： 如果删除了叶子结点导致AVL不平衡，那么AVL会改变，所以$T_1$和$T_3$可能不相同，而2.3说的都太绝对，可举反例证明其错误，选A

解析：为了满足任意性，其1~5层的所有结点都要存储起来，所以是1+2+4+8+16=31 选A

解析：已知二叉树的先序和中序遍历，画出二叉树的结构，可知二叉树后序序列我b，f，e，d，c，a，选C

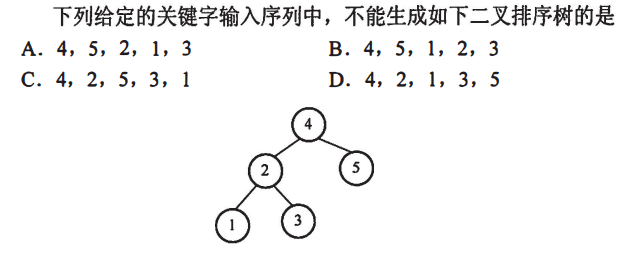
解析：明显是B无法满足

解析：画出二叉树的图

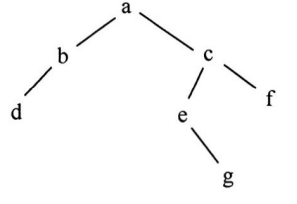
a的右孩子都是树的头结点，所以选C

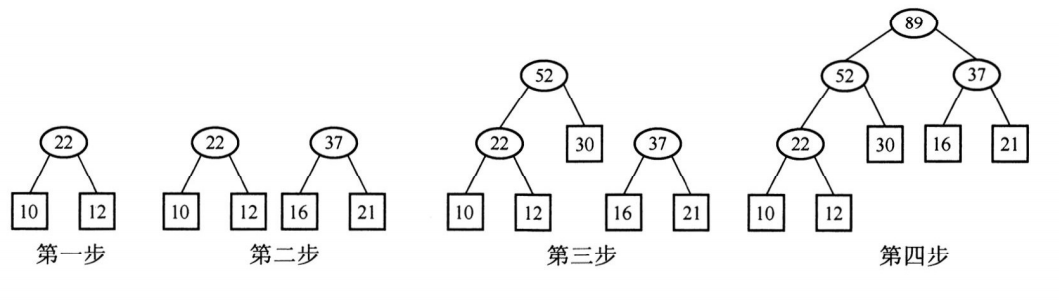
解析：根据哈夫曼树的构造方法进行构造，显然选B

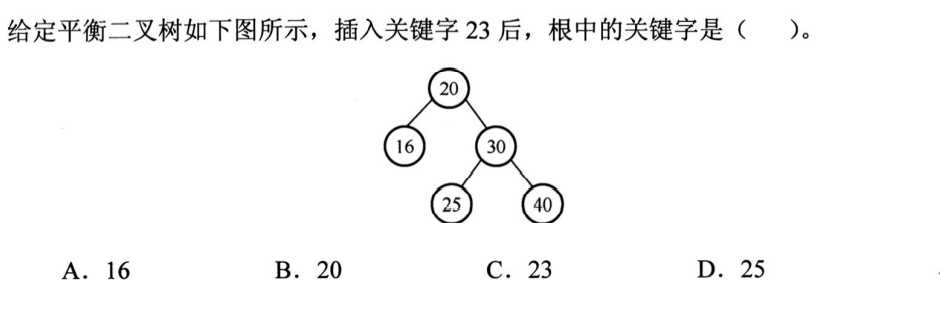
解析：显然是RL型交换，25是关键字

解析：根据堆的性质，父节点只可能比子结点大or小，所有必然是有序的，选D

解析：根据性质，显然1成立，对于2，边数有可能等于顶点个数减1，不成立，对于3，对于无向完全图来说，不成立，所以选A

解析：根据公式最多边数：n(n-1)，则在满足剩下6个顶点形成无向完全图的情况下，再多一条边则能保证连通，最少是6(6-1)+1=16，选C

解析：按拓扑排序的规则，序列开头必定是a，结尾必定是d，中间肯定b在c之前，故序列有 bce，ebc，bec三种，选B

解析：1，2错误，3正确，选C，都是基本概念

解析：邻接表的BFS，显然时间复杂度为C

解析：主对角线以下元素为0，说明是有向无环图，但是拓扑排序不能确定，所以选C

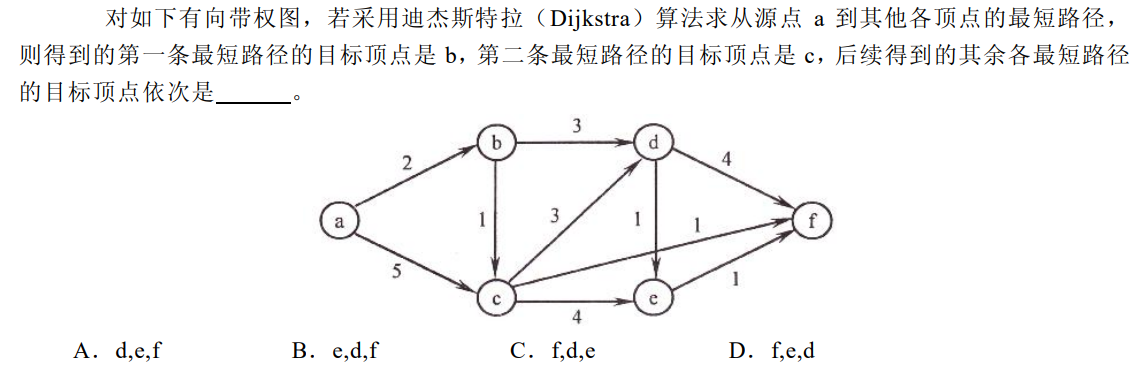
解析：将abc视作一个整体，则下一条权值最短路径是c-f，之后是c-d，最后是d-e，选C

解析：对于1，代价为最小是唯一的，正确，对于2，不一定会完全出现，对于3，错误，对于4，错误，所以选A

解析：度为列和行的非0元素个数，所以选C

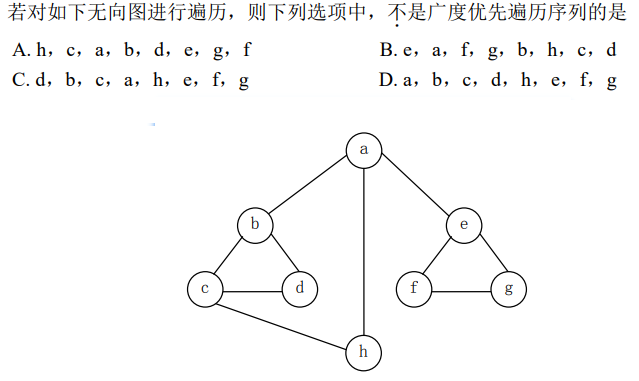
解析：D错误，a之后应该是bhe三个节点

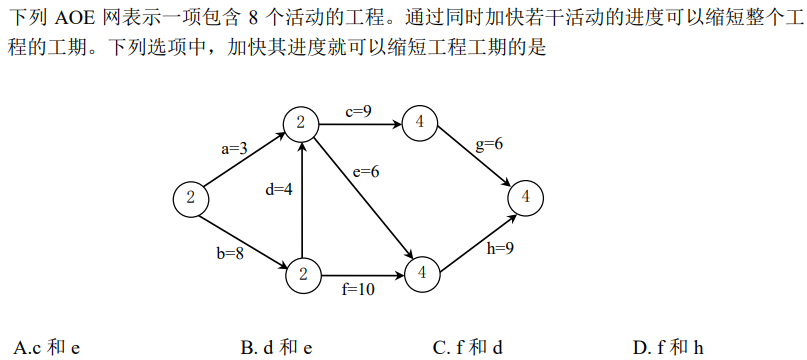
解析：最短路径为bdeh，bfh，bdcg，只有同时减少f和d，可以减少3条关键路径上的关键活动，所以选C

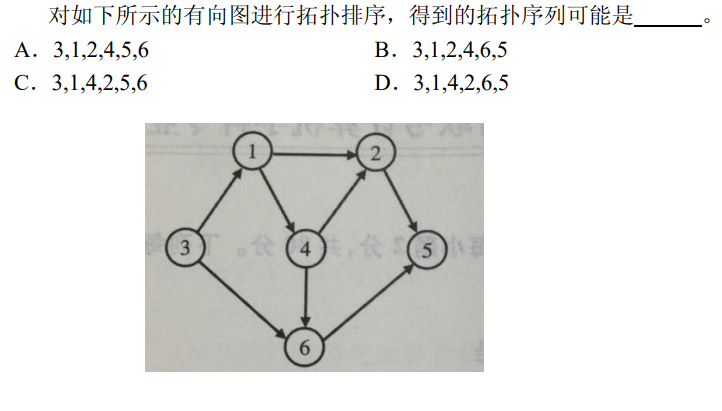
解析：D符合条件

解析：从0开始 有 0132 0213 0231 0312 0321 5种序列

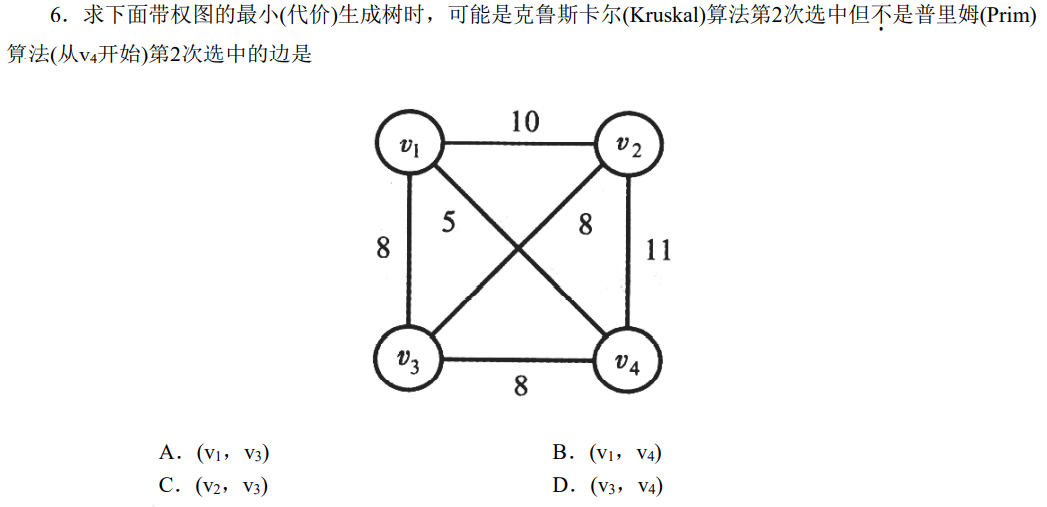
解析：克鲁斯卡尔可以直接选权最小的边，而普利姆算法则会选能连通的边，在第二次选择中，图中3条权值为8的边，克鲁斯卡尔算法均能选择，而普利姆算法不选选择$v_3,v_2$的边，所以选C

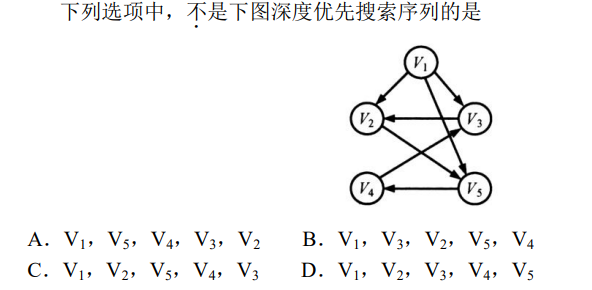
解析：D有明显问题，2之后应该是$V_5$，而非$V_3$

解析：概念问题，B

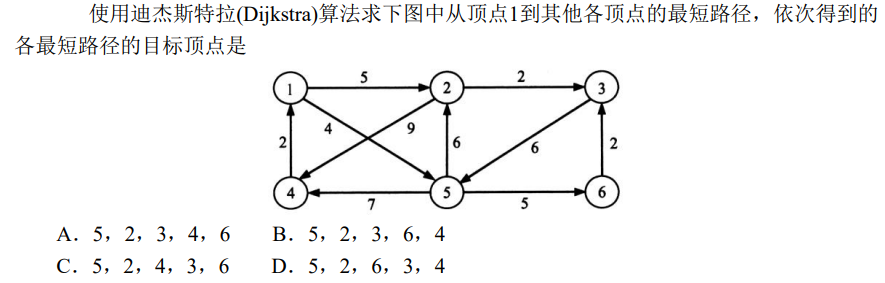
解析：依次是：5,2,3,6,4 选B

解析：在无向图中，度数=边数×2 所以图G的总度数为32，而已知的度数有12+12=24 最少还需要(32-24)/2=4个度为2的点，顶点总数最少是3+4+4=11个，选B

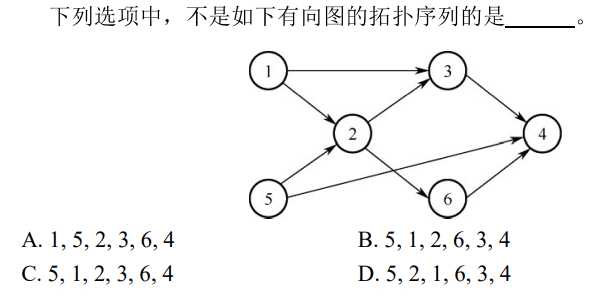
解析：概念问题，选D

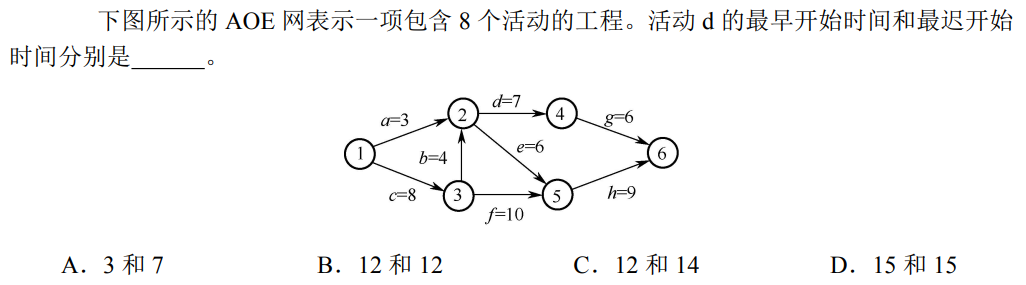
解析：显然活动d并不在关键路径上，最早开始时间是：4+8=12，最晚开始时间是将d变为关键路径，即从6开始，9+10=6+7+4+x，x=2，最多延迟2，故为12+2=14，选C

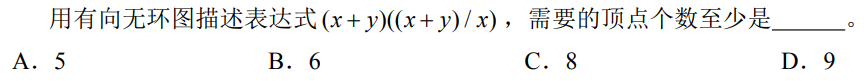
解析： 先确定xy会占2个顶点，然后标记运算顺序，后一个+号先生效，第一个+号和/号同时生效，最后中间的×号生效，化为有向无环图，选A

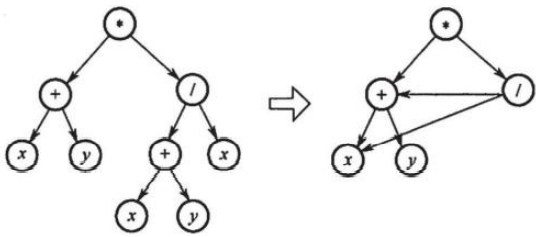
解析：退出递归前输出，那么会首先输出最末尾的结点，即是逆拓扑有序序列，选B

解析：克鲁斯卡尔算法会选取最小的边加入到集合中，所以按最小边选就是了，选A

解析：概念问题，选B

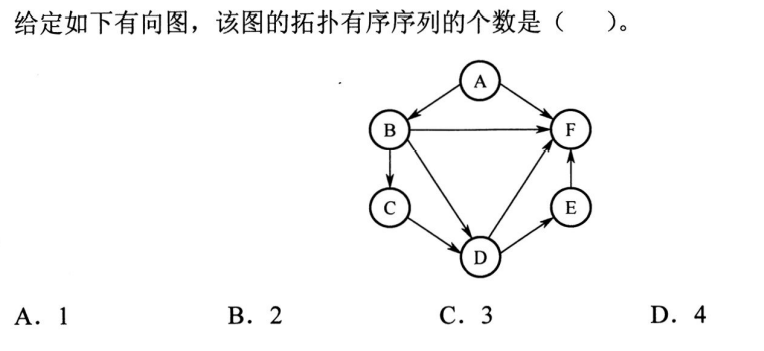
解析：显然只有一个顺序，即ABCDEF，选A

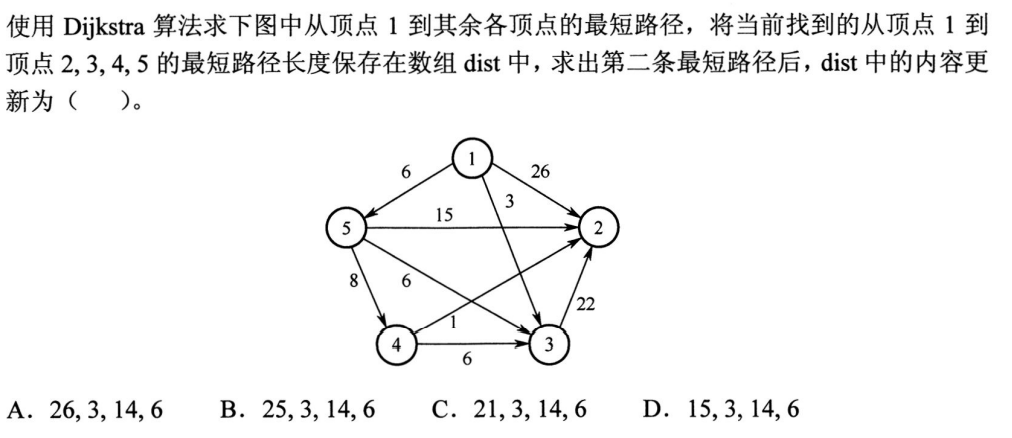
解析：注意要做路径的累加，毕竟是算到顶点1的最短路径，所以是C

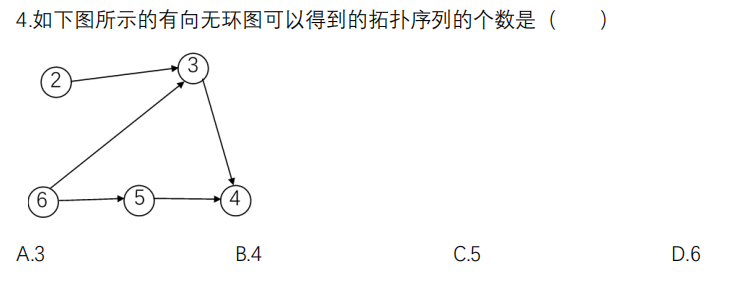
解析：有26354 26534 62354 62534 65234 共5种，所以选C

解析：AB显然有错，对于D来说，非强连通图并不一定会出现“孤岛”，A到B有单向路径也是非强连通图，所以选C

解析：当权值一致的时候，最短路径问题简化为BFS问题，所以选A

解析：叶节点之间通过指针链接是B+树的特点，还支持顺序存储，所以选D

解析：16个元素构筑的完全二叉树最多有5层，所以比较次数最多为5，选B

解析：A，94大于91，不符合规律

解析：装填因子就是表中记录数/表的长度，增大并不能提高效率，2，3可以直接提高效率选D

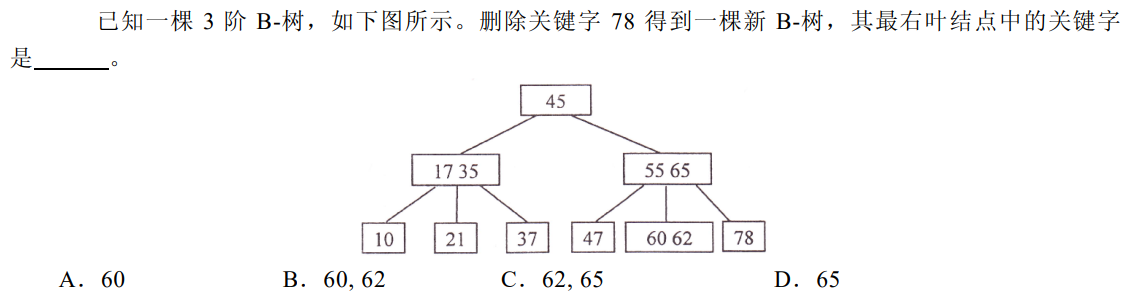
解析：删除了78，则65顶替，选D

解析：最多有5个元素，导致根节点分裂，成为高度为2的B树，选A

解析：散列函数并不会受碰撞影响，装填因子就是表中记录数/表的长度，不会受影响，而ASL一定会受到影响，选D

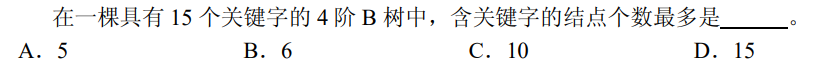
解析：每个结点最少要含1个关键字，所以最多为15个

解析：明显是A，180<200

解析：只要写出模式串t的next数组就行咯，abaabc的length数组为 0 0 1 1 2 0，next数组为-1 0 0 1 1 2，KMP算法中i的并不会回溯，依然是5,j回溯，回溯到2，所以选C

解析：概念问题，A

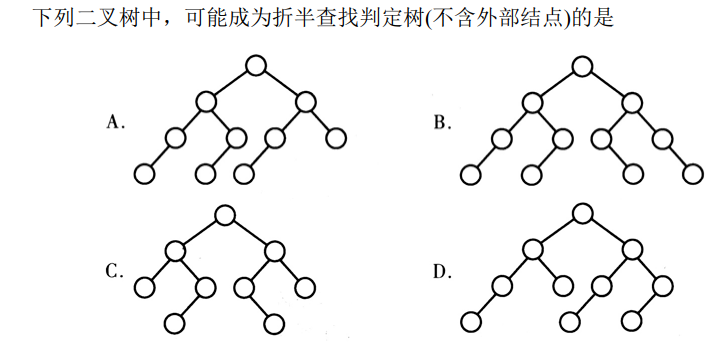
解析：只需要判定折半查找判定树的结构是否符合规律就行了，A符合左子树结点数大于等于右子树结点数的规律，所以选A

解析：B+树就是为了磁盘中数据搜索和数据库而生的，所以选B

解析：3阶B树，每个结点最多含2个关键字，最少含1个关键字，所以近似看做完全二叉树，结果是B

解析：3个关键字的余数相同，所以ASL=(1+2+3)/3=2，选C

解析：注意到只需要比较0~6之间的关键字，其次要注意到和空数据的比较也算一次查找

ASL=（9+8+7+6+5+4+3）/7=6，选C

解析：首先得出模式串的next数组：

第一趟会比较6次，然后回到2的位置再比较4次，所以是10次，选B

解析：根据B树插入的性质，结点满后再插入，从[m/2]处（向上取整）分裂，其中间的[m/2]会并入到父节点，选B

解析：最多情况如下：

所以选A

解析：伪随机再散列法的作用是，当发生冲突时，让关键字加上伪随机序列，然后再进行散列，70%13=5，和18冲突，加上5后，75%13=10，和75冲突，加上8后，78%17=0，与39冲突，加上3后，73%13=8，无冲突，故放入位置是8，选B

解析：先按照完全二叉树的性质建立堆，然后将3插入，进行换位，得到答案A

解析：如果是冒泡排序，则最小(大)值应该在末尾，如果是选择排序，则最小(大)值应该在开始,如果是二路归并，那么序列应该被分成2个有序部分，所以选B

解析：首先对快排来说，递归次数和初始排列肯定是有关的，但是与划分的分区处理无关，所以选D

解析：很明显的冒泡排序痕迹，选A

解析：快排的话，要不断的进行交换，所以顺序存储最好，选A

解析：先建立大根堆，在堆底部，一路交换上去，可以比较次数为2次，选B

解析：选择排序和堆排序都可以一趟可以选出最大(小)值，而快速排序一趟可以确定枢轴的最终位置，所以选A

解析：插入排序的总趟数是固定的，移动次数也不会改变，选D

解析：第一趟的结果是 110 120 911 122 114 007 119，第二趟结果是 007 110 911 114 119 120 122 ，选C

解析：观察序列，发现以9,13,20 |1,7 23| 4,8 15保持递增，所以间隔为3

解析：快速排序每一趟确定枢轴的位置，C不符合要求

解析：冒泡排序和快速排序都是交换排序，首先排除，而直接插入排序也与初始排序相关，所以选C

解析：先建立小根堆，删除8之后，用表尾元素12代替，然后让12下坠，过程中12和15比较一次，12和10比较一次，12和16比较一次，共3次，选C

解析：希尔排序就是插入排序的升级版，而且不适合用折半插入，所以选A

解析：从数组开头以每组3个来查找，所以在开头处更好，选B

解析：10TB属于外部排序，外部排序本质上使用归并排序，选D

解析：归并排序使用的空间和代码都比插入排序多，但是时间复杂度比插入排序好很多，所以选B

解析：如果数据要采用随机查找的方式找到指定元素，那么链表的效率很低，比如堆排序和希尔排序，所以选D

解析：1在第1位，然后第一轮的间隔是5，第二轮6到了第3位，显然第二轮间隔是3，选D

解析：根据建堆过程，从表尾元素开始，先是5和4,7比较，交换5和7的位置，然后是1和9,8比较，交换1和9的位置，所以选A

解析：显然都要考虑到，选D

解析：A：72,28符合枢轴，B：72,2符合，C：2,28,32都符合，D仅32符合，不可能是第二趟结果，所以选D

解析：根据公式：即$n_k=\frac{(n_v+n_s-1)}{k-1}$

为了让$n_k$为正整数，需要补充的虚段就是满足这一条件的最小正整数，所以选B

解析：显然1.2是对的，大根堆堆顶元素最大，次大肯定在根的下一层，4也正确，所以选C

解析：直接插入每趟会比较有序序列的后一个，将其插入到前面的有序序列中去，而简单选择每趟会选择一个最小(大)的数插入到前面去，所以有序序列的比较而言，肯定是直接插入排序少，选A

解析：分配，收集后，372被夹在了301和892中间，所以选C

解析：要求依次建立大根堆，所以每插入一个数字就调整依次，最终结果为B

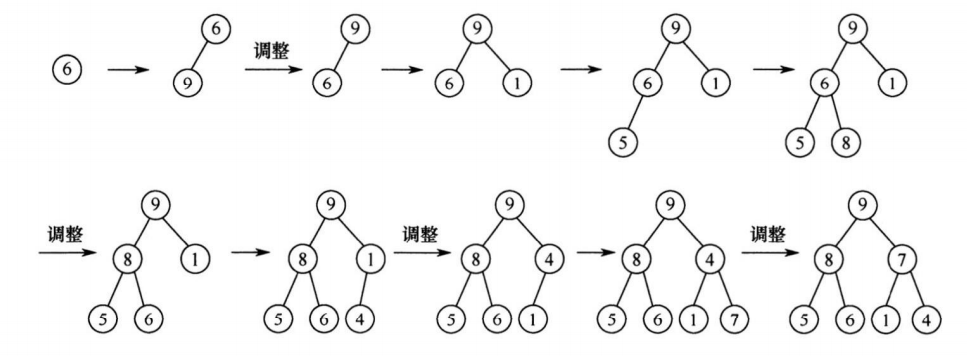
解析：直接插入排序的每一趟只用比一次即可，所以选B