198.打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

1
2
3
4
输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

1
2
3
4
输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

Solution

此题为dp的例题，将会完整分析

  • 回溯的选择视角

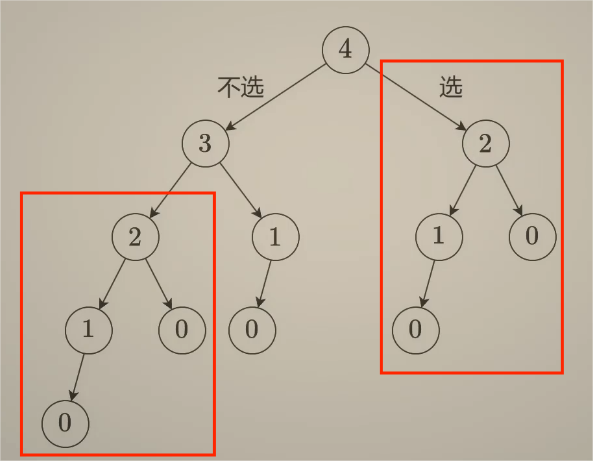
首先将其视作回溯问题，而非dp问题，那么思维导图如下：

image-20240515203458056

可以根据选择视角来写出代码：

选：从前i-2个房子中得到的最大金额和

不选：从前i-1个房子中得到的最大金额和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
   private int [] nums;
   private int ans;
   public int rob(int[] nums) {
         this.nums=nums;
         return dfs(nums.length-1);
    }
    public int dfs(int i){
        if(i<0){
            return 0;
        }
        ans=Math.max((dfs(i-2)+nums[i]),dfs(i-1));
        return ans;
    }
}

然而代码会超时，因为时间复杂度太高了

  • 记忆化搜索

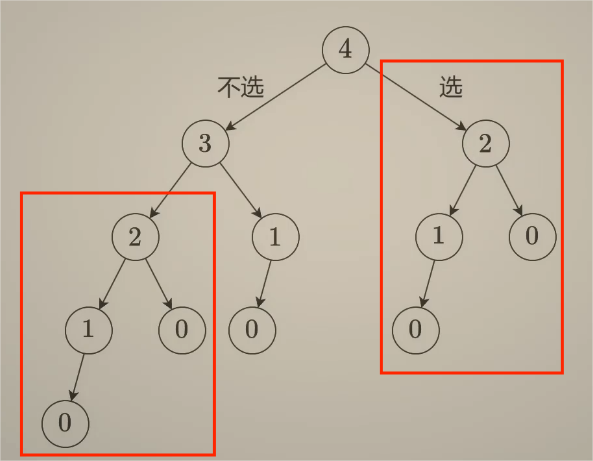
我们需要用一个手段来降低时间复杂度，注意到：

dpdpdp

实际上是重合的，我们可以简化这个搜索树，前提是使用一个数组来记录dfs的结果，称之为记忆化搜索

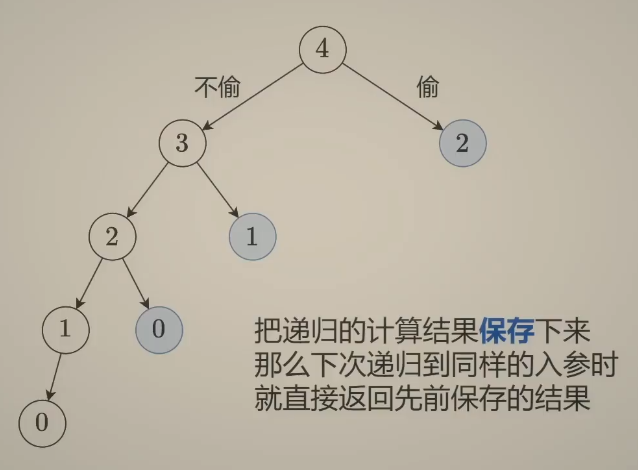
简化后的搜索树如图：

image-20240515205059816

代码如下：

增加了cache的数组，并初始化为-1，大小和nums一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
   private int [] nums;
   private int ans;
   private int [] cache;
   public int rob(int[] nums) {
         this.nums=nums;
         cache=new int [nums.length];
         Arrays.fill(cache, -1);
         return dfs(nums.length-1);
    }
    public int dfs(int i){
        if(i<0){
            return 0;
        }
        if (cache[i]!=-1){
            return cache[i];
        }
        ans=Math.max((dfs(i-2)+nums[i]),dfs(i-1));
        cache[i]=ans;
        return ans;
    }
}
  • 递推公式

记忆化搜索是从最后开始，往前一步步推理的，也就是说自顶向下

如果从起始位置算，往上推理，就叫做递归，也就是自底向上

已知回溯的写法如下：

用$f(i)$形式改写：

这样的话，首先是不必进行递归了，可以直接从f[i+2]开始，使用一个for循环就可以完成整个过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {

   public int rob(int[] nums) {
         int [] f=new int [nums.length+2];
         for (int i = 0; i < nums.length; i++) {
            f[i+2]=Math.max(f[i+1],f[i]+nums[i]);
        }
         return f[nums.length+1];
    }
    /*
    public int dfs(int i){
        if(i<0){
            return 0;
        }
        if (cache[i]!=0){
            return cache[i];
        }
        ans=Math.max((dfs(i-2)+nums[i]),dfs(i-1));
        cache[i]=ans;
        return ans;
    }
    */
}
  • 动态规划(dp)

仔细观察公式：

实际上，我们算当前状态，只需要知道前两个状态就行了，也就是说，可以直接使用临时变量来记录前两个状态，记忆数组是可以被舍弃的！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {

   public int rob(int[] nums) {
        
        int f0,f1;
        f0=f1=0;
         for (int i = 0; i < nums.length; i++) {
            int new_f=Math.max(f1,f0+nums[i]);
            f0=f1;
            f1=new_f;
        }
         return f1;
    }
}