188.买卖股票的最佳时机4

给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1：

1
2
3
输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2：

1
2
3
4
输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
     随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

Solution

这里多一个限制条件k，要求最多在k次内完成交易

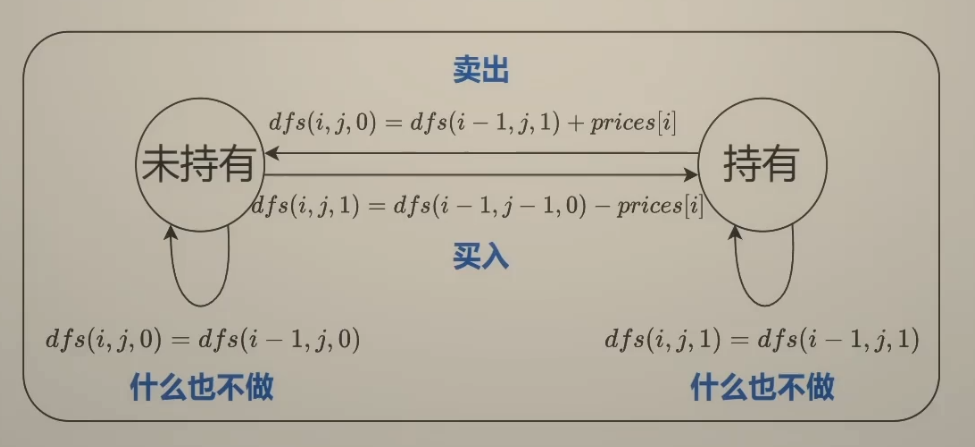
image-20240521161024680

边界条件：

$dfs(·,-1,·)=-\infty$ 任何情况下，j都不能为负

$dfs(-1,j,0)=0$ 第0天开始未持有股票，利润为0

$dfs(-1,j,1)=-\infty$ 第0天开始不可能持有股票

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    // 主方法，计算在最多进行 k 次交易情况下的最大利润
    public int maxProfit(int k, int[] prices) {
        int n = prices.length; // 获取数组的长度
        int[][][] dp = new int[n + 1][k + 2][2]; // 初始化三维数组 dp，大小为 (n+1) x (k+2) x 2

        // 初始化 dp 数组，防止溢出
        for (int i = 0; i < n; i++) {
            for (int j = 0; j <= k + 1; j++) {
                Arrays.fill(dp[i][j], Integer.MIN_VALUE / 2); // 将 dp[i][j] 的值设为极小值
            }
        }

        // 初始化第一天的状态，不持有股票的利润为 0
        for (int j = 1; j <= k + 1; j++) {
            dp[0][j][0] = 0;
        }

        // 遍历每一天
        for (int i = 0; i < n; i++) {
            // 遍历每一次交易
            for (int j = 1; j < k + 2; j++) {
                // 更新第 i+1 天不持有股票的利润
                dp[i + 1][j][0] = Math.max(dp[i][j][0], dp[i][j - 1][1] + prices[i]);
                // 更新第 i+1 天持有股票的利润
                dp[i + 1][j][1] = Math.max(dp[i][j][1], dp[i][j][0] - prices[i]);
            }
        }

        // 返回第 n 天进行最多 k 次交易且不持有股票的最大利润
        return dp[n][k + 1][0];
    }
}

恰好：$f[0][1][0]=0$，其余$=-\infty$

至少：$f[0][0][0]=0$，其余$=-\infty$