Pytorch入门

Numpy2Pytorch

数组对象tensor

首先，我们介绍n维数组，也称为张量（tensor）。无论使用哪个深度学习框架，它的张量类（在MXNet中为ndarray，在PyTorch和TensorFlow中为Tensor）都与Numpy的ndarray类似。

但深度学习框架又比Numpy的ndarray多一些重要功能：首先，GPU很好地支持加速计算，而NumPy仅支持CPU计算；其次，张量类支持自动微分。这些功能使得张量类更适合深度学习

以下是ndarray和tensor之间的对比，方便快速入手tensor

属性

当涉及到比较 PyTorch 的 Tensor 和 NumPy 的 ndarray 的属性时，它们之间有很多相似之处。下面是一些主要属性的对比：

属性	NumPy 的 `ndarray`	PyTorch 的 `Tensor`
数据类型	`ndarray.dtype`	`tensor.dtype`
形状	`ndarray.shape`	`tensor.shape`
维度	`ndarray.ndim`	`tensor.dim()`
元素个数	`ndarray.size`	`tensor.numel()`
设备（CPU/GPU）	-	`tensor.device`
改变形状	`ndarray.reshape(new_shape)`	`tensor.view(new_shape)`
展开	`ndarray.flattern`	`tensor.view(-1)`
转置	`ndarray.T`	`tensor.T`
张量类型	-	`torch.FloatTensor`, `torch.IntTensor`, 等

需要注意的是，虽然有很多相似之处，但也有一些语法和方法上的区别。例如，PyTorch 使用 .view() 来改变形状，而 NumPy 使用 .reshape()

创建数组

操作	NumPy	PyTorch
创建零数组	`np.zeros(shape)`	`torch.zeros(shape)`
创建单位矩阵	`np.eye(n)`	`torch.eye(n)`
创建全一数组	`np.ones(shape)`	`torch.ones(shape)`
从现有数据创建数组	`np.array([1, 2, 3])`	`torch.tensor([1, 2, 3])`
创建等间隔的数组	`np.arange(start, stop, step)`	`torch.arange(start, end, step)`
创建指定范围的数组	`np.linspace(start, stop, num)`	`torch.linspace(start, end, steps=num)`
随机数数组	`np.random.rand(shape)`	`torch.rand(shape)`
随机整数数组	`np.random.randint(low, high, size)`	`torch.randint(low, high, size)`

大多类似，PyTorch可以直接使用rand类创建随机数，而Numpy要借助random类

运算

当涉及到比较 PyTorch 的 Tensor 和 NumPy 的 ndarray 的运算时，它们之间有很多相似之处。下面是一些主要运算的对比：

运算	NumPy 的 `ndarray`	PyTorch 的 `Tensor`
元素级加法	`a + b`	`a + b`
元素级乘法	`a * b`	`a * b`
元素级除法	`a / b`	`a / b`
元素级取余	`a % b`	`torch.remainder(a, b)`
矩阵乘法	`np.dot(matrix_a, matrix_b)`	`torch.mm(matrix_a, matrix_b)`
转置	`ndarray.T`	`tensor.t()`
归约操作（求和）	`np.sum(array)`	`tensor.sum()`
归约操作（平均值）	`np.mean(array)`	`tensor.mean()`
最大值	`np.max(array)`	`tensor.max()`
最小值	`np.min(array)`	`tensor.min()`
按维度归约操作	`np.sum(array, axis=0)`	`tensor.sum(dim=0)`
元素级比较	`a > b`, `a == b`, etc.	`torch.gt(a, b)`, `torch.eq(a, b)`, etc.
索引和切片	`ndarray[1:3]`	`tensor[1:3]`
L2 范数	`np.linalg.norm(a, ord=2)`	`torch.norm(a, p=2)`
广播	可以通过 NumPy 自动广播进行运算	广播是默认行为，无需额外操作

需要注意的是，虽然许多运算在语法上非常相似，但有些函数名称和方法可能会有所不同。此外，PyTorch 的 Tensor 具有自动微分功能，这是深度学习中反向传播的基础，而 NumPy 不具备这个功能。

连接与删除

操作	NumPy 的 `ndarray`	PyTorch 的 `Tensor`
连接数组	`np.concatenate([a, b])`	`torch.cat([a, b], dim=0)`
沿轴连接数组	`np.stack([a, b], axis=0)`	`torch.stack([a, b], dim=0)`
删除元素	`np.delete(ndarray, indices, axis)`	`tensor.index_select(dim, indices)`
插入元素	`np.insert(ndarray, index, values, axis)`	不直接支持
去重	`np.unique(ndarray)`	`torch.unique(tensor)`
翻转数组	`np.flip(ndarray, axis)`	`torch.flip(tensor, dims)`

转换

使用torch.tensor(x)可以轻松把numpy转换为tensor类型

使用x=torch_tensor.numpy()可以把tensor换算为numpy类型

自动微分

链式法则

$\frac{\partial y}{\partial x_i} = \frac{\partial y}{\partial u_1} \frac{\partial u_1}{\partial x_i} + \frac{\partial y}{\partial u_2} \frac{\partial u_2}{\partial x_i} + \cdots + \frac{\partial y}{\partial u_m} \frac{\partial u_m}{\partial x_i}$

假设$x,w$是一个$n$维的向量， $z=(<x,w>-y)^2$ ，求解$\frac{\partial z}{\partial w}$

我们首先对式子进行分解：假设 $a=<x,w>,b=a-y,z=b^2$ ，那么

$\begin{align*} \frac{\partial z}{\partial w}&=\frac{\partial z}{\partial b}\frac{\partial b}{\partial a}\frac{\partial a}{\partial w}\\ &=\frac{\partial b^2}{\partial b}\frac{\partial a-y}{\partial a}\frac{\partial<x,w>}{\partial w}\\ &= 2b\cdot1\cdot x^T\\ &=2(<x,w>-y)x^T \end{align*}$

用计算图的形式表示

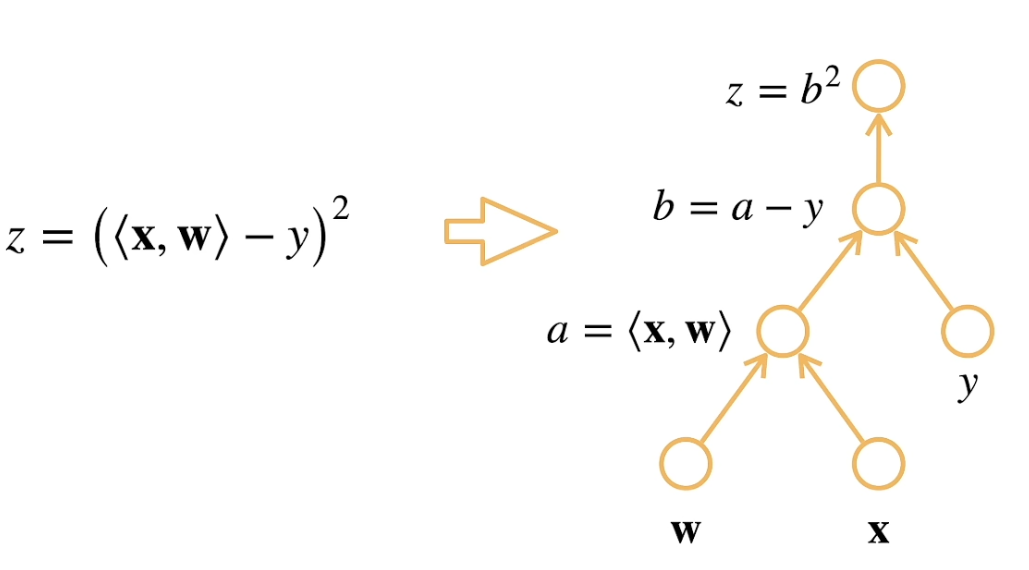
通过前向传播，计算每一层的输出，并存储中间变量的梯度

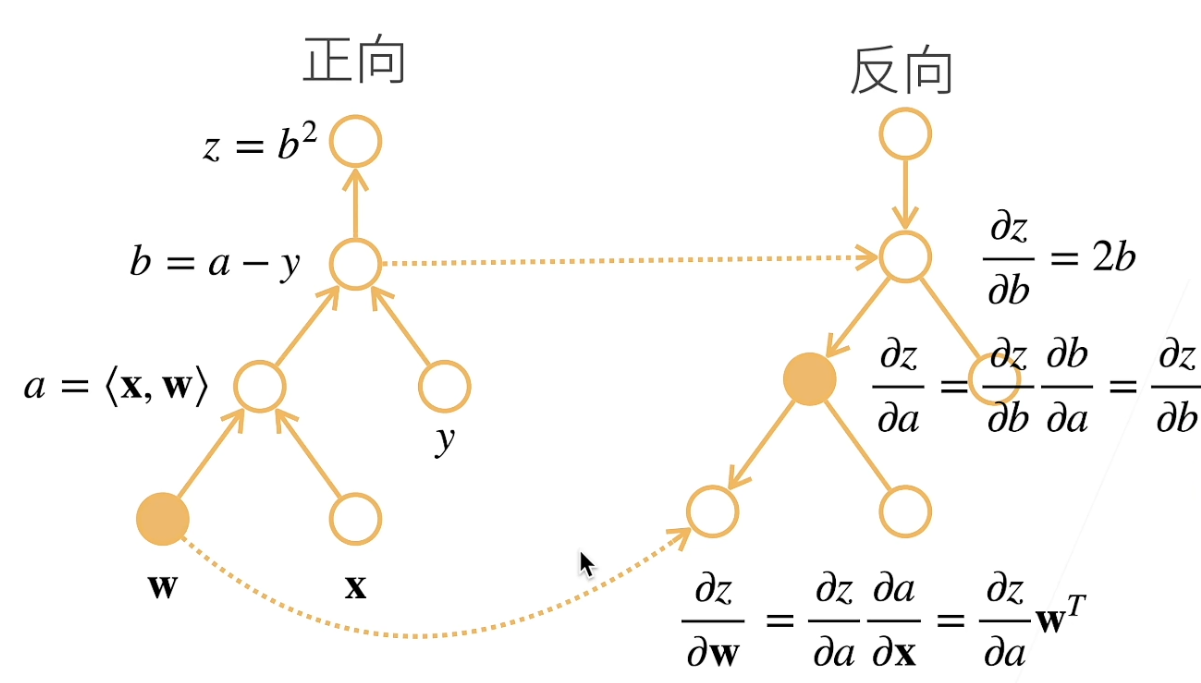
然后根据前向传播存储计算得到的梯度的值，可以反过来求导，这叫反向传播

$\frac{\partial y}{\partial x}=(((\frac{\partial y}{\partial u_n}(\frac{\partial u_n}{\partial u_{n-1}})\cdots )\frac{\partial u_2}{\partial u_1})\frac{\partial u_1}{\partial x}$

代码实现

tensor除了包含了很多与numpy相同功能的函数外，其独特的点在于，内置很多深度学习相关的属性和函数

梯度追踪属性：

requires_grad： 一个布尔值，指定是否对该张量进行梯度追踪。默认情况下，创建张量时 requires_grad 是 False，但可以通过设置为 True 来启用梯度追踪。例如：torch.tensor([1.0], requires_grad=True)。
grad： 用于存储计算得到的梯度。在执行反向传播后，该属性将包含相对于某个标量的梯度值。例如，在计算了某个标量损失相对于张量 x 的梯度后，可以通过 x.grad 获取梯度。

自动微分属性：

grad_fn： 一个指向创建该张量的函数的引用。该属性是一个 torch.autograd.Function 对象，用于构建计算图。在进行反向传播时，这个计算图用于计算梯度。例如，如果张量是通过加法操作创建的，grad_fn 将是一个指向加法函数的引用。

反向传播：

tensor.backward()函数：tensor.backward() 会计算损失相对于创建 y 的计算图中所有叶子节点（通常是模型参数）的梯度。在反向传播期间，PyTorch 会根据链式法则（链式求导）计算梯度，并将这些梯度存储在相应的张量的 grad 属性中。

例：对$y=2xx^T$，对关于列向量$x$求导

在计算y关于x的梯度之前，需要将requires_grad设置为True，之后可以用x的grad属性来存储梯度

import torch

# 创建一个张量并启用梯度追踪
x = torch.arange(4.0, requires_grad=True)

# 打印初始梯度（在进行任何计算之前，梯度为None）
print("初始梯度:", x.grad)  # 输出 None

# 执行一个计算，y = 2 * x·x （点积）
y = 2 * torch.dot(x, x)

# 进行反向传播以计算梯度
y.backward()

# 打印计算得到的梯度
print("计算后的梯度:", x.grad)

结果是：

1 2	初始梯度: None 计算后的梯度: tensor([ 0., 4., 8., 12.])

如果最终的y不是一个标量，而是一个向量，那么我们一般会用sum函数对y求和，使其变为一个标量运算

import torch
x = torch.arange(4.0, requires_grad=True)
y=x*x
y.sum().backward()
print(x.grad)

#结果是：tensor([0., 2., 4., 6.])

有时，我们希望将某些计算移动到记录的计算图之外。例如，假设y是作为x的函数计算的，而z则是作为y和x的函数计算的。想象一下，我们想计算z关于x的梯度，但由于某种原因，希望将y视为一个常数，并且只考虑到x在y被计算后发挥的作用。

这里可以分离y来返回一个新变量u，该变量与y具有相同的值，但丢弃计算图中如何计算y的任何信息。换句话说，梯度不会向后流经u到x。因此，下面的反向传播函数计算z=u*x关于x的偏导数，同时将u作为常数处理，而不是z=x*x*x关于x的偏导数。

import torch

# 定义变量 x，并启用梯度追踪
x = torch.tensor([2.0], requires_grad=True)

# 计算 y = x^2
y = x*x

# 分离 y，并得到一个新的变量 u
u = y.detach()

# 计算 z = u * x
z = u * x

# 执行反向传播，计算 z 关于 x 的梯度
z.backward()

# 打印 x 的梯度
print("梯度值:", x.grad)
#结果不是8，而是4

y.detach() 将 y 分离，得到一个新的变量 u。然后，z = u * x 中的 u 被视为常数，不再与计算图有关。因此，z.backward() 只计算了 z 关于 x 的梯度，而不计算 u 关于 x 的梯度。最终，打印出了 x 的梯度。

当希望冻结某些层或变量，不让其参与梯度更新时有用

总结一下，计算的步骤为：

定义模型： 创建模型并设置参数的 requires_grad 以启用梯度追踪。
前向传播： 使用模型进行前向传播，计算输出。
计算损失： 定义损失函数，计算模型输出与真实标签之间的损失。
反向传播： 调用 backward() 方法，PyTorch 会根据计算图自动计算梯度。
参数更新： 根据梯度和优化算法更新模型参数。