线性回归

线性回归的概念以及普通的numpy实现已经在机器学习的多变量线性回归的章节中实现过了，所以这节侧重于写一下在Pytorch框架下，实现线性回归

传统方法

导入

1
2
3
4
%matplotlib inline
import random
import torch
from d2l import torch as d2l

%matplotlib inline是Jupyter笔记本中的特殊命令，它允许Matplotlib生成的图形直接在笔记本中显示，而不是在单独的窗口中显示。这通常用于数据科学和机器学习环境，以便方便地可视化数据和结果。

生成数据集

为了简单起见，我们将根据带有噪声的线性模型构造一个人造数据集。 我们的任务是使用这个有限样本的数据集来恢复这个模型的参数。 我们将使用低维数据，这样可以很容易地将其可视化。 在下面的代码中，我们生成一个包含1000个样本的数据集， 每个样本包含从标准正态分布中采样的2个特征。 我们的合成数据集是一个矩阵$X$

我们使用线性模型参数$\theta=[2,-3.4]^T,b=4.2$和噪声$\epsilon$生成数据集和标签

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def synthetic_data(theta, b, num_examples):
    """生成y=Xw+b+噪声"""
    # 生成服从正态分布的随机数据矩阵X，形状为(num_examples, len(w))
    X = torch.normal(0, 1, (num_examples, len(w)))
    
    # 计算标签y，其中y = X\theta + b
    y = X@theta + b
    
    # 添加均值为0、标准差为0.01的噪声，模拟真实数据中的随机性
    y += torch.normal(0, 0.01, y.shape)
    
    # 返回生成的数据矩阵X和相应的标签y，标签y的形状为列向量
    return X, y.reshape((-1, 1))

# 定义真实的权重和偏置,即Theta参数
true_t = torch.tensor([2, -3.4])
true_b = 4.2

# 调用synthetic_data函数生成包含1000个样本的合成数据集
features, labels = synthetic_data(true_t, true_b, 1000)

torch.normal是PyTorch中用于生成服从正态分布（高斯分布）的随机数的函数。其基本语法如下：

torch.normal(mean, std, size, out=None)

  • mean: 正态分布的均值。
  • std: 正态分布的标准差。
  • size: 指定生成随机数张量的形状。
  • out（可选）: 输出张量，用于存储结果。

均值决定正态分布的峰值的横坐标，而标准差决定了正态分布图像的宽度

注意，features中的每一行都包含一个二维数据样本， labels中的每一行都包含一维标签值（一个标量）。

绘图

1
2
3
4
5
6
7
8
d2l.set_figsize()

# 提取第二列的特征和标签，并将其转换为 NumPy 数组
x = features[:, 1].detach().numpy()
y = labels.detach().numpy()

# 绘制散点图
d2l.plt.scatter(x,y,1)

通过生成第二个特征features[:, 1]和labels的散点图， 可以直观观察到两者之间的线性关系。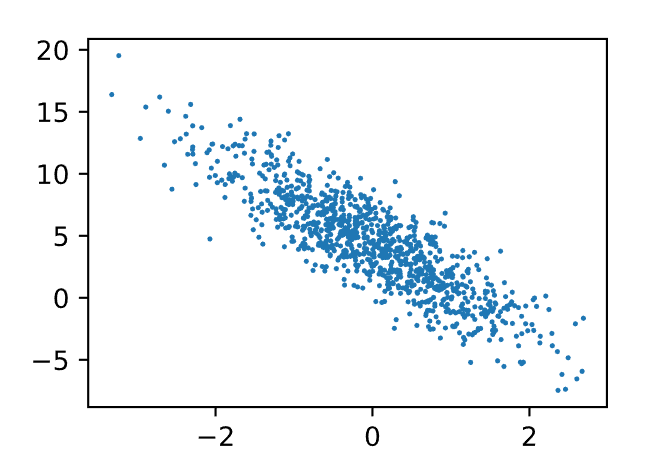image-20231211133001618

在绘制图形时，Matplotlib函数通常期望接收NumPy数组而不是PyTorch张量。因此，使用.detach().numpy()的组合可以将PyTorch张量转换为NumPy数组。这样，我们可以在Matplotlib中轻松地使用这些数组，而不必担心梯度计算。也就是说detach函数删除了tensor中的grad属性

读取数据集

通常，我们利用GPU并行运算的优势，处理合理大小的“小批量”。 每个样本都可以并行地进行模型计算，且每个样本损失函数的梯度也可以被并行计算。 GPU可以在处理几百个样本时，所花费的时间不比处理一个样本时多太多。

同时我们也会采取 小批量梯度下降法来进行最优化，关于小批量梯度下降，在机器学习中已经有过介绍了，参见大规模机器学习

在下面的代码中，我们定义一个data_iter函数， 该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量。 每个小批量包含一组特征和标签。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def data_iter(batch_size, features, labels):
    # 获取数据集中样本的总数
    num_examples = len(features)
    # 创建一个包含样本索引的列表，用于后续的随机打乱
    indices = list(range(num_examples))
    # 将样本索引随机打乱，以进行随机批次训练
    random.shuffle(indices)
    
    # 从 0 开始，每次迭代按批次大小移动，以获取每个批次的起始索引
    for i in range(0, num_examples, batch_size):
        # 选择当前批次的样本索引，并将其转换为 PyTorch 张量
        batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])
        # 使用 yield 返回当前批次的特征和标签，以迭代器的方式逐批获取数据
        yield features[batch_indices], labels[batch_indices]

yield 是一个用于定义生成器函数的关键字，用于生成迭代器。生成器函数是一种特殊的函数，它可以通过 yield 语句生成一个值，并在下一次调用时从上次离开的地方继续执行。

yield features[batch_indices], labels[batch_indices] 的作用是将当前批次的特征和标签返回给调用者，然后暂停函数的执行。下次迭代时，函数会从上次离开的地方继续执行，而不是从头开始。这种方式使得生成器函数可以有效地处理大量数据，因为它不需要一次性加载所有数据到内存中。

然后输出

1
2
3
4
5
batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

初始化模型参数

在我们开始用小批量随机梯度下降优化我们的模型参数之前， 我们需要先有一些参数。 在下面的代码中，我们通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重， 并将偏置初始化为0

1
2
theta = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

在初始化参数之后，我们的任务是更新这些参数，直到这些参数足够拟合我们的数据。 每次更新都需要计算损失函数关于模型参数的梯度。 有了这个梯度，我们就可以向减小损失的方向更新每个参数。

因为手动计算梯度很枯燥而且容易出错，所以没有人会手动计算梯度。 我们使用上一章中引入的自动微分来计算梯度。

定义模型

接下来，我们必须定义模型，将模型的输入和参数同模型的输出关联起来。 回想一下，要计算线性模型的输出， 我们只需计算输入特征$X$和模型权重$\theta$的矩阵-向量乘法后加上偏置$b$。 注意，上面的$X\theta$是一个向量，而$b$是一个标量

根据广播机制： 当我们用一个向量加一个标量时，标量会被加到向量的每个分量上。

1
2
3
def linreg(X, theta, b):  #@save
    """线性回归模型"""
    return X@theta + b

定义损失函数

因为需要计算损失函数的梯度，所以我们应该先定义损失函数。

在实现中，我们需要将真实值y的形状转换为和预测值y_hat的形状相同。

1
2
3
def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

定义优化算法

在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度。 接下来，朝着减少损失的方向更新我们的参数。 下面的函数实现小批量随机梯度下降更新。 该函数接受模型参数集合、学习速率和批量大小作为输入。每 一步更新的大小由学习速率lr决定。 因为我们计算的损失是一个批量样本的总和，所以我们用批量大小（batch_size） 来规范化步长，这样步长大小就不会取决于我们对批量大小的选择。

1
2
3
4
5
6
7
8
9
10
def sgd(params, lr, batch_size):
    """小批量随机梯度下降"""
    with torch.no_grad():
        # 遍历所有模型参数
        for param in params:
            # 更新参数：param = param - learning_rate * param.grad / batch_size
            param -= lr * param.grad / batch_size
            # 梯度清零，为下一轮梯度计算做准备
            param.grad.zero_()

在 PyTorch 中，torch.no_grad() 是一个上下文管理器，用于指定在其范围内的代码块中不需要计算梯度。这在一些情况下是有用的，例如在参数更新时，我们不希望计算梯度，只想执行更新操作。

通过使用 torch.no_grad()，我们可以显式地告诉 PyTorch 在这个上下文中不追踪梯度，从而提高效率和减少计算开销。

在深度学习中，params 通常是指模型的参数集合。模型的参数是那些需要在训练过程中进行更新的可学习的权重和偏置等。并不需要事先定义param，param在每次迭代中自动取得params列表中的当前元素，使得你可以对它进行操作，比如更新模型参数的值或清零梯度等。

在 PyTorch 中，模型的参数通常通过 nn.Module 类的 parameters() 方法来获取。

训练

现在我们已经准备好了模型训练所有需要的要素，可以实现主要的训练过程部分了。 理解这段代码至关重要，因为从事深度学习后， 相同的训练过程几乎一遍又一遍地出现。 在每次迭代中，我们读取一小批量训练样本，并通过我们的模型来获得一组预测。 计算完损失后，我们开始反向传播，存储每个参数的梯度。 最后，我们调用优化算法sgd来更新模型参数。

​ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
lr = 0.03  # 学习率，控制参数更新的步长
num_epochs = 3  # 训练循环的迭代次数
net = linreg  # 模型，这里使用线性回归模型
loss = squared_loss  # 损失函数，这里使用平方损失函数

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        # 计算小批量数据的损失，X为特征，y为标签
        l = loss(net(X, theta, b), y)  
        # 因为l形状是(batch_size,1)，而不是一个标量。
        # l中的所有元素被加到一起，并以此计算关于[theta,b]的梯度
        l.sum().backward()
        # 使用参数的梯度更新参数，实现小批量随机梯度下降
        sgd([theta, b], lr, batch_size)  
    with torch.no_grad():
        # 在整个训练集上计算整体损失，用于观察训练进展
        train_l = loss(net(features, theta, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

更新参数这一步骤，本来是要写成如下形式：

1
参数 -= (学习率/一批的数量) * 偏导数(形式是 误差*X矩阵)

注意这两步：

  • l.sum().backward()的作用是，更新theta和b的梯度属性grad，即更新了偏导数

  • sgd([theta, b], lr, batch_size) 函数实现了theta的下降，函数内部直接使用了更新后的偏导数

简洁实现

生成数据集

1
2
3
4
5
6
7
8
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

直接使用传统方法生成了

读取数据集

我们可以调用框架中现有的API来读取数据。 我们将features和labels作为API的参数传递，并通过数据迭代器指定batch_size。 此外，布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def load_array(data_arrays, batch_size, is_train=True):
    """
    构造一个PyTorch数据迭代器

    Parameters:
        - data_arrays: 包含特征和标签的数据元组
        - batch_size: 每个小批量的样本数
        - is_train: 一个布尔值，指示是否是训练数据，默认为 True

    Returns:
        - data_iter: PyTorch 数据迭代器
    """
    # 创建 TensorDataset 对象，将特征和标签组合成一个数据集
    dataset = data.TensorDataset(*data_arrays)
    # 使用 DataLoader 构造数据迭代器，按批次加载数据
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

# 示例用法
batch_size = 10
# 创建一个 PyTorch 数据迭代器，用于按批次加载特征和标签数据
data_iter = load_array((features, labels), batch_size)

使用data.TensorDataset将数据打包，使用data.DataLoader按batch_size解包，并且shuffle=True,打乱输出

代码里面：is_train是一个布尔值（True或False），通常作为一个参数传递给函数或方法，用以指示当前数据加载器是否用于训练数据。当is_train为True时，表示数据加载器被用于训练集，此时shuffle应该设置为True以打乱数据。当is_train为False时，意味着数据加载器用于测试集或验证集，此时shuffle通常设置为False，以保持数据顺序不变。

data 是一个模块或库的名称，它包含 TensorDataset 和 DataLoader 等用于处理数据的类

  • torch.utils.data.TensorDataset 主要用于包装多个张量（特征和标签）作为一个数据集。这个类的主要优势在于它可以方便地将多个张量按相同的索引进行配对，形成一个样本。在训练过程中，我们通常有特征和对应的标签，TensorDataset 可以将它们组合成一个数据集，以便使用 PyTorch 中的 DataLoader 来按批次加载数据。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    import torch
    from torch.utils.data import TensorDataset

    # 假设有特征张量 features 和标签张量 labels
    features = torch.tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]])
    labels = torch.tensor([0, 1, 1])

    # 使用 TensorDataset 将特征和标签组合成数据集
    dataset = TensorDataset(features, labels)

  • torch.utils.data.DataLoader 是 PyTorch 中用于创建数据迭代器的类，主要用于按批次加载数据。它提供了多线程数据加载、数据打乱以及按照指定批次大小生成数据的功能。在深度学习中，通常使用 DataLoader 将数据集划分为小批量，以便输入到模型中进行训练或评估。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    from torch.utils.data import DataLoader
                  
    # 使用 DataLoader 按批次加载数据
    batch_size = 2
    data_loader = DataLoader(dataset, batch_size, shuffle=True)
                  
    # 在训练循环中按批次迭代
    for batch_features, batch_labels in data_loader:
        # 进行模型训练或其他操作
        print("Batch Features:", batch_features)
        print("Batch Labels:", batch_labels)

这里我们使用iter构造Python迭代器，并使用next从迭代器中获取第一项。

1
next(iter(data_iter))
  • data_iter 是一个 PyTorch 数据迭代器，你可以使用 iter(data_iter) 将其转换为一个迭代器对象。
  • next(...) 函数用于获取迭代器的下一个元素。

定义模型

观察线性回归的神经网络图：

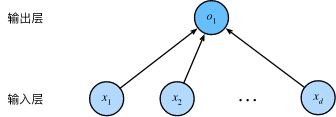
image-20231212094027669

这是一个单层神经网络，每个输入都与每个输出（在本例中只有一个输出）相连，将这种变换 称为全连接层或称为 稠密层

对于标准深度学习模型，我们可以使用框架的预定义好的层。这使我们只需关注使用哪些层来构造模型，而不必关注层的实现细节。 我们首先定义一个模型变量net，它是一个Sequential类的实例。

Sequential类将多个层串联在一起。 当给定输入数据时，Sequential实例将数据传入到第一层， 然后将第一层的输出作为第二层的输入，以此类推。 在下面的例子中，我们的模型只包含一个层，因此实际上不需要Sequential。

接下来，我们会使用Pytorch中的Sequential类定义全连接层

1
2
3
4
# nn是神经网络的缩写
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))
  • nn.Linear(2, 1)：这是一个线性层，它将输入的特征维度从 2 降到 1。第一个参数是输入特征的数量，即输入的维度为 2；第二个参数是输出特征的数量，即输出的维度为 1。这个线性层执行的操作类似于一个简单的线性变换，其中包含权重和偏置。
  • nn.Sequential(...)：这是一个 Sequential 容器，它按照顺序包含了一个或多个神经网络层。在这里，它只包含了一个线性层。
  • 返回一个 PyTorch 的神经网络模型，具体而言是 nn.Sequential 类的一个实例

初始化模型参数

在使用net之前，我们需要初始化模型参数。 如在线性回归模型中的权重和偏置。 深度学习框架通常有预定义的方法来初始化参数。 在这里，我们指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样， 偏置参数将初始化为零。

1
2
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

这里的net[0]指的就是线性层Linear(2,1)，默认属性有weight和bias等，通过net[0].weight.data来设置线性层权重的数据

考虑一个简单的线性层的计算，以一个神经元为例：

其中：

  • weight 是权重参数，表示输入的权重；
  • input 是输入特征；
  • bias 是偏置参数，是一个常数项；
  • activation 是激活函数，将加权和加上偏置的结果进行非线性映射。

定义损失函数

1
loss = nn.MSELoss()

在 PyTorch 中，nn.MSELoss() 是均方误差损失（Mean Squared Error Loss）的实现。均方误差是回归问题中常用的损失函数，用于衡量模型预测值与真实值之间的平方差。

定义优化算法

小批量随机梯度下降算法是一种优化神经网络的标准工具， PyTorch在optim模块中实现了该算法的许多变种。 当我们实例化一个SGD实例时，我们要指定优化的参数 （可通过net.parameters()从我们的模型中获得）以及优化算法所需的超参数字典。 小批量随机梯度下降只需要设置lr值，这里设置为0.03。

1
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
  • torch.optim 是 PyTorch 中包含各种优化算法的模块。
  • SGD 表示随机梯度下降优化算法，是深度学习中最基本和常用的优化算法之一。
  • net.parameters() 返回神经网络模型中所有可学习参数（权重和偏置）的迭代器。
  • lr=0.03 是学习率，用于控制参数更新的步幅。学习率是一个超参数，需要根据具体问题进行调整。
  • 返回一个 PyTorch 的 SGD（随机梯度下降）优化器对象trainer。这个优化器对象被用于更新神经网络模型中所有可学习参数的数值，以最小化定义的损失函数。

训练

在每个迭代周期里，我们将完整遍历一次数据集（train_data）， 不停地从中获取一个小批量的输入和相应的标签。 对于每一个小批量，我们会进行以下步骤:

  • 通过调用net(X)生成预测并计算损失l（前向传播）。
  • 通过进行反向传播来计算梯度。
  • 通过调用优化器来更新模型参数。

为了更好的衡量训练效果，我们计算每个迭代周期后的损失，并打印它来监控训练过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 设置训练的总轮数
num_epochs = 3

# 遍历每一轮训练
for epoch in range(num_epochs):
    # 遍历数据迭代器，获取每个小批量的特征 X 和标签 y
    for X, y in data_iter:
        # 计算当前小批量的损失
        l = loss(net(X), y)
        
        # 梯度清零，防止梯度累积
        trainer.zero_grad()
        
        # 反向传播，计算梯度，已经在loss里面进行了累加，所以没用sum
        l.backward()    
        
        # 使用优化器更新模型参数
        trainer.step()
    
    # 计算整个训练集上的损失
    l = loss(net(features), labels)
    
    # 输出当前轮次的训练损失
    print(f'epoch {epoch + 1}, loss {l:f}')

下面我们比较生成数据集的真实参数和通过有限数据训练获得的模型参数。 要访问参数，我们首先从net访问所需的层，然后读取该层的权重和偏置。 正如在从零开始实现中一样，我们估计得到的参数与生成数据的真实参数非常接近。

1
2
3
4
w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)