ex7：k-means and PCA

前半

概述

在这个练习中，你将实现K均值算法并将其用于图像压缩。首先，你将在一个2D示例数据集上开始，这将帮助你直观地了解K均值算法的工作原理。之后，你将使用K均值算法进行图像压缩，通过将图像中出现的颜色数量减少到仅包含那些在该图像中最常见的颜色。在这一部分的练习中，你将使用ex7.m。

必要的文件如下：

  • ex7.py - 用于K均值算法第一练习的Python脚本
  • ex7data2.mat - K均值算法的示例数据集
  • bird_small.png- 示例图像
  • displayData.py - 显示存储在矩阵中的2D数据的函数
  • plotDataPoints.py- K均值聚类中质心的初始化函数
  • plotProgresskMeans.py- 绘制K均值每一步的函数
  • runkMeans.py - 运行K均值算法

需要完成的文件：

  • findClosestCentroids.py- 寻找最接近的质心（在K均值中使用）
  • computeCentroids.py- 计算质心均值（在K均值中使用）
  • kMeansInitCentroids.py - K均值聚类的质心初始化

导入

1
2
3
4
5
6
7
8
9
10
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as scio
from skimage import io
from skimage.util import img_as_float

import runkMeans as km
import findClosestCentroids as fc
import computeCentroids as cc
import kMeansInitCentroids as kmic

Scikit-image（skimage）是一个基于SciPy库的图像处理库，提供了一系列用于图像处理的工具和算法。它包含了许多常用的图像处理任务的实现，如图像过滤、边缘检测、形态学操作、图像变换等。

寻找质心

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# ===================== 第1部分: 寻找最近的质心 =====================
# 为了帮助实现K均值算法，我们将学习算法分为两个函数 -- find_closest_centroids 和 compute_centroids。
# 在这一部分，你应该完成 findClosestCentroids.py 中的代码。

print('寻找最近的质心。')

# 载入将要使用的示例数据集
data = scio.loadmat('ex7data2.mat')
X = data['X']

# 选择一组初始质心
k = 3  # 三个质心
initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])

# 使用初始质心找到示例的最近质心
idx = fc.find_closest_centroids(X, initial_centroids)

print('前3个示例的最近质心：')
print('{}'.format(idx[0:3]))
print('(应分别为0, 2, 1的最近质心)')

input('程序暂停。按回车键继续')

这里需要完成findClosestCentroids.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np


def find_closest_centroids(X, centroids):
    K = centroids.shape[0]
    m = X.shape[0]
    idx = np.zeros(m)

    for i in range(m):
        # 计算欧几里得距离的平方，避免使用平方根以提高效率
        distances_squared = np.sum((X[i] - centroids) ** 2, axis=1)
        # 找到最近的质心的索引
        closest_centroid_index = np.argmin(distances_squared)

        # 将索引存储在idx中
        idx[i] = closest_centroid_index

    return idx

虽然centroids是一个$(3 \times 2)$的数组，而X[i]是一个一维的数组，但是两者之间依然可以加减，X[i]会复制成3列，然后减去centroids，这是numpy的特性：广播运算

指定axis=1，在numpy，是指定行的运算，结果即是数据点到质心之间距离的平方，distances_squared是一个一维数组

最后使用 np.argmin函数，找出数组中最小值的索引，放入到idx中

移动质心

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# ===================== 第2部分: 计算均值 =====================
# 在实现最近质心函数后，你现在应该完成 compute_centroids 函数。

print('计算质心均值。')

# 根据上一部分找到的最近质心计算均值。
centroids = cc.compute_centroids(X, idx, k)

print('在找到最近质心后计算的质心： \n{}'.format(centroids))
print('应为')
print('[[ 2.428301 3.157924 ]')
print(' [ 5.813503 2.633656 ]')
print(' [ 7.119387 3.616684 ]]')

input('程序暂停。按回车键继续')

完成compute_centroids 函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import numpy as np

def compute_centroids(X, idx, K):
    # 有用的值
    (m, n) = X.shape

    # 你需要正确返回以下变量。
    centroids = np.zeros((K, n))

    # ===================== 你的代码在这里 =====================
    # 遍历每个质心，计算属于它的所有点的平均值。
    # 具体而言，行向量 centroids[i] 应包含分配给质心 i 的数据点的平均值。

    for i in range(K):
        # 找到属于质心 i 的所有数据点的索引
        points_in_cluster = (idx == i)

        if np.any(points_in_cluster):  # 检查簇是否非空
            # 计算这些数据点的平均值，并将结果存储在 centroids[i] 中
            centroids[i] = np.mean(X[points_in_cluster], axis=0)

    # ==========================================================
    return centroids

这里需要遍历每个质心，计算属于它的所有点的平均值。

在for循环中，points_in_cluster = (idx == i)会得到一个大小和idx一样的布尔数组

centroids[i] = np.mean(X[points_in_cluster], axis=0)，则将布尔数组作为索引，成功地找到了每个质心对应的数据点，而将其他的数据点置为0，这一个方法在逻辑回归和SVM中已经用过多次

最后指定axis=0，即指定按列运算，算出x,y坐标的均值，得到质心移动的位置

K均值聚类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# ===================== 第3部分: K均值聚类 =====================
# 在完成 compute_centroids 和 find_closest_centroids 两个函数后，你将拥有运行
# K均值算法所需的所有部分。在这一部分，你将在我们提供的示例数据集上运行K均值算法。

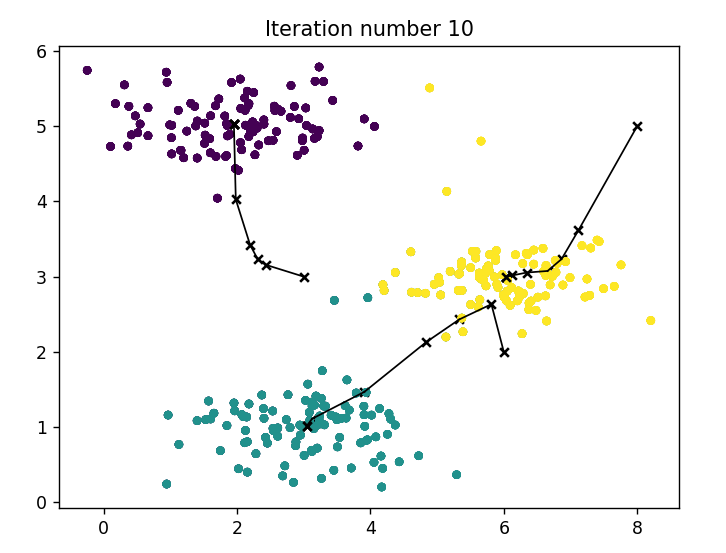
print('在示例数据集上运行K均值聚类。')

# 载入示例数据集
data = scio.loadmat('ex7data2.mat')
X = data['X']

# 运行K均值算法的设置
K = 3
max_iters = 10

# 为了一致性，这里我们设置质心为特定的值
# 但在实际中，你可能想要自动生成它们，例如通过
# 将它们设置为随机示例（如在 kMeansInitCentroids 中所示）。
initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])
# 运行K均值算法。结尾的 'True' 告诉我们的函数绘制
# K均值算法的进展
centroids, idx = km.run_kmeans(X, initial_centroids, max_iters, True)
plt.show()
print('K均值完成。')

input('程序暂停。按回车键继续')

使用K均值聚类，画出质心移动的图像

image-20231128061033509

图像的聚类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# ===================== 第4部分: 对像素进行K均值聚类 =====================
# 在这个练习中，你将使用K均值对图像进行压缩。为此，
# 你将首先对图像中像素的颜色运行K均值，然后将每个像素映射到
# 最近的质心。

print('在图像的像素上运行K均值聚类。')

# 载入一张鸟的图像
image = io.imread('bird_small.png')
image = img_as_float(image)

# 图像的尺寸
img_shape = image.shape

# 将图像重塑为Nx3矩阵，其中N = 像素的数量。
# 每行将包含红、绿和蓝像素值
# 这给我们提供了我们将在K均值上使用的数据集矩阵X。

X = image.reshape(img_shape[0] * img_shape[1], 3)

# 在这个数据上运行你的K均值算法
# 你应该在这里尝试不同的K值和max_iters值
K = 16
max_iters = 10

# 在使用K均值时，随机初始化质心是很重要的。
# 你应该在继续之前完成 kMeansInitCentroids.py 中的代码
initial_centroids = kmic.kmeans_init_centroids(X, K)

# 运行K均值
centroids, idx = km.run_kmeans(X, initial_centroids, max_iters, False)

print('K均值完成。')

input('程序暂停。按回车键继续')

这里需要完成kMeansInitCentroids.py随机初始化质心的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np


def kmeans_init_centroids(X, K):
    # 你需要正确返回这个值
    centroids = np.zeros((K, X.shape[1]))

    # ===================== 你的代码在这里 =====================
    # 将 centroids 设置为从数据集 X 中随机选择的示例
    # 你可以使用 np.random.choice 函数来实现

    # 从数据集中随机选择 K 个索引
    random_indices = np.random.choice(X.shape[0], K, replace=False)

    # 使用选定的索引获取相应的示例并将其赋值给 centroids
    centroids = X[random_indices]

    # ==========================================================

    return centroids

random_indices = np.random.choice(X.shape[0], K, replace=False)的意思是：从 0 到 X.shape[0] - 1 的范围中，随机选择 K 个不重复的整数，用于初始化 K-Means 算法的质心。这样确保了初始化的质心是不同的样本点。

压缩图像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# ===================== 第 5 部分: 图像压缩 =====================
# 在这个练习的这一部分，你将使用 K-Means 的聚类结果来压缩一张图像。
# 为了实现这一目标，我们首先找到每个示例所属的最近簇。

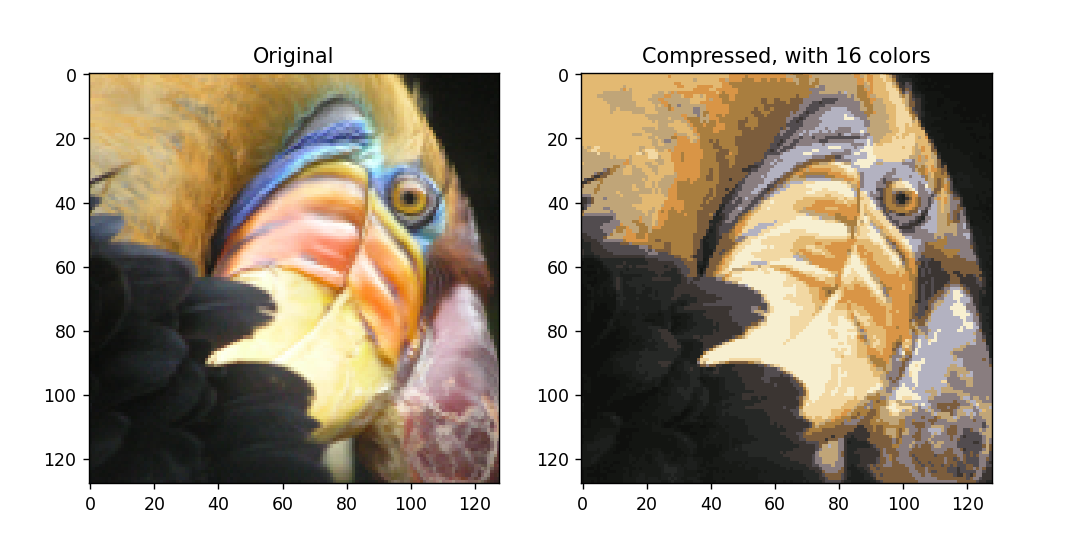
print('将 K-Means 应用于图像压缩。')

# 找到最近的簇成员
idx = fc.find_closest_centroids(X, centroids)
print(idx)
idx = np.array(idx, dtype=int)
print(idx)
# 本质上，我们现在已经用 idx 表示了图像 X，
# 接下来，我们可以通过将每个像素（由其在 idx 中的索引指定）映射到质心值来恢复图像
X_recovered = centroids[idx]

# 将恢复的图像重塑为正确的尺寸
X_recovered = np.reshape(X_recovered, (img_shape[0], img_shape[1], 3))

plt.subplot(2, 1, 1)
plt.imshow(image)
plt.title('Original')

plt.subplot(2, 1, 2)
plt.imshow(X_recovered)
plt.title('Compressed, with {} colors'.format(K))
plt.show()
input('练习 7 完成。按 ENTER 键退出')

输出图像

image-20231128062534585

后半

概述

在这个练习中，你将使用主成分分析（PCA）进行降维操作。你将首先尝试使用一个2D示例数据集，以便直观地理解PCA的工作原理，然后将其应用于一个包含5000张人脸图像的较大数据集。

必要的文件：

ex7_pca.m - 用于主成分分析（PCA）第二练习的Python脚本

ex7data1.mat - PCA的示例数据集

ex7faces.mat - 人脸数据集

feature_normalize.py-特征归一化

需要补充的文件

pca.py - 执行主成分分析

projectData.py- 将数据集投影到较低维度的空间

recoverData.py - 从投影中恢复原始数据

导入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 导入需要的库
import matplotlib.pyplot as plt  # 用于绘图
import numpy as np  # 用于数学运算
import scipy.io as scio  # 用于读取MATLAB文件
from mpl_toolkits.mplot3d import Axes3D  # 用于3D绘图
from skimage import io  # 用于图像处理
from skimage.util import img_as_float  # 用于图像处理

import featureNormalize as fn  # 导入特征归一化模块
import pca as pca  # 导入主成分分析模块
import runkMeans as rk  # 导入K均值聚类模块
import projectData as pd  # 导入数据投影模块
import recoverData as rd  # 导入数据恢复模块
import displayData as disp  # 导入数据可视化模块
import kMeansInitCentroids as kmic  # 导入K均值聚类初始化质心模块
import runkMeans as km  # 导入K均值聚类模块

载入并绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# ===================== 第1部分: 载入示例数据集 =====================
# 通过使用一个小型数据集进行练习，该数据集易于可视化
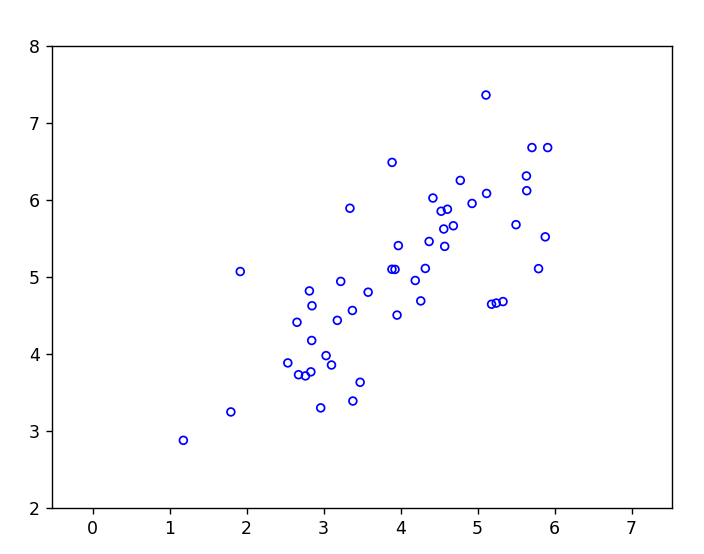
print('可视化主成分分析示例数据集.')

# 下面的命令加载数据集
data = scio.loadmat('ex7data1.mat')
X = data['X']

# 可视化示例数据集
plt.figure()
plt.scatter(X[:, 0], X[:, 1], facecolors='none', edgecolors='b', s=20)
plt.axis('equal')
plt.axis([0.5, 6.5, 2, 8])

input('程序暂停。按回车键继续')

image-20231128083330996

主成分分析

编写PCA的函数，根据PCA的公式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
import scipy

def pca(X):
    # 有用的值
    (m, n) = X.shape

    # 你需要正确返回以下变量。
    U = np.zeros(n)
    S = np.zeros(n)


    Sigma = (1 / m) * X.T @ X
    # 使用SVD计算特征向量和特征值
    U, S, _ = scipy.linalg.svd(Sigma)

    return U, S

回到ex7_pca.py文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# ===================== 第2部分: 主成分分析 =====================
# 实现主成分分析（PCA）降维技术。首先需要对X进行归一化,你应该完成pca.py
X_norm, mu, sigma = fn.feature_normalize(X)

# 运行PCA
U, S = pca.pca(X_norm)

rk.draw_line(mu, mu + 1.5 * S[0] * U[:, 0])
rk.draw_line(mu, mu + 1.5 * S[1] * U[:, 1])
plt.show()
print('最大特征向量: \nU[:, 0] = {}'.format(U[:, 0]))
print('预期结果应为 [-0.707107 -0.707107]')

input('程序暂停。按回车键继续')

输出图片：

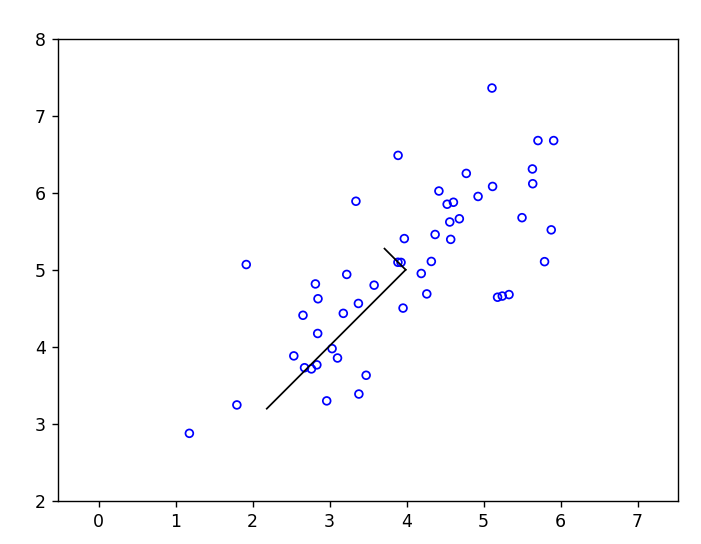
image-20231128085737767

数据降维

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# ===================== 第3部分: 数据降维 =====================
# 实现投影步骤，将数据映射到前k个特征向量
print('在示例数据集上进行降维.')

# 绘制归一化后的数据集（从PCA返回）
plt.figure()
plt.scatter(X_norm[:, 0], X_norm[:, 1], facecolors='none', edgecolors='b', s=20)
plt.axis('equal')
plt.axis([-4, 3, -4, 3])

# 将数据投影到K=1维
K = 1
Z = pd.project_data(X_norm, U, K)
print('第一个示例的投影: {}'.format(Z[0]))
print('(此值应约为1.481274)')

先归一化，然后编写project_data函数，对数据进行降维

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np

def project_data(X, U, K):
    # 你需要正确返回以下变量。
    Z = np.zeros((X.shape[0], K))

    # ===================== 你的代码在这里 =====================
    # 说明: 使用U中的前K个特征向量（前K列）计算数据的投影。
    #       对于第i个示例 X[i]，对第k个特征向量的投影如下：
    #           x = X[i, :].T
    #           projection_k = x.T @ U[:, k]

    for i in range(X.shape[0]):
        x = X[i, :].reshape(X.shape[1], 1)
        Z[i, :] = (U[:, :K].T@x).flatten()

    # ==========================================================

    return Z

x = X[i, :].reshape(X.shape[1], 1)：这行代码将数据矩阵 X 中的第 i 行提取出来，并将其转换为列向量

Z[i, :] = (x.T @ U[:, :K]).flatten()：这行代码执行以下操作：

  • (U[:, :K].T@x)：将 x 与前 K 个主成分进行内积运算，得到投影后的列向量。这个操作实际上就是将数据投影到前 K 个主成分上。
  • .flatten()：将投影后的列向量展平成一维数组。
  • Z[i, :] = ...：将得到的一维数组存储在矩阵 Z 的第 i 行中，表示第 i 个样本在前 K 个主成分上的投影。

数据复原

编写recover_data.py，将降维后的数据还原

$z=U^{T}_{reduce}x$，相反的方程为：$x_{appox}=U_{reduce}\cdot z$,$x_{appox}\approx x$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np


def recover_data(Z, U, K):
    # 初始化一个全零矩阵用于存储恢复后的数据
    X_rec = np.zeros((Z.shape[0], U.shape[0]))

    # ===================== 你的代码在这里 =====================
    # 说明: 使用U中的前K个特征向量（前K列）在原始空间中计算数据的近似。
    #       对于第i个示例 Z[i]，对于维度j的近似恢复数据如下：
    #           v = Z[i, :].T
    #           recovered_j = v.T @ U[j, :K].T

    # 遍历每个样本
    for i in range(Z.shape[0]):
        # 获取第i个样本在主成分空间上的投影向量
        v = Z[i, :].reshape(Z.shape[1], 1)
        
        # 遍历每个维度，进行近似恢复
        for j in range(U.shape[0]):
            # 计算第i个样本在维度j上的近似恢复数据
            X_rec[i, j] = (v.T @ U[j, :K].T).flatten()

    # ==========================================================

    return X_rec

回到ex7_pca.py文件

1
2
3
4
5
6
7
8
9
10
11
er_data(Z, U, K)

print('第一个示例的近似值: {}'.format(X_rec[0]))
print('(此值应约为 [-1.047419 -1.047419])')

# 绘制连接投影点与原始点的线条
plt.scatter(X_rec[:, 0], X_rec[:, 1], facecolors='none', edgecolors='r', s=20)
for i in range(X_norm.shape[0]):
    rk.draw_line(X_norm[i], X_rec[i])
plt.figure()
plt.show()

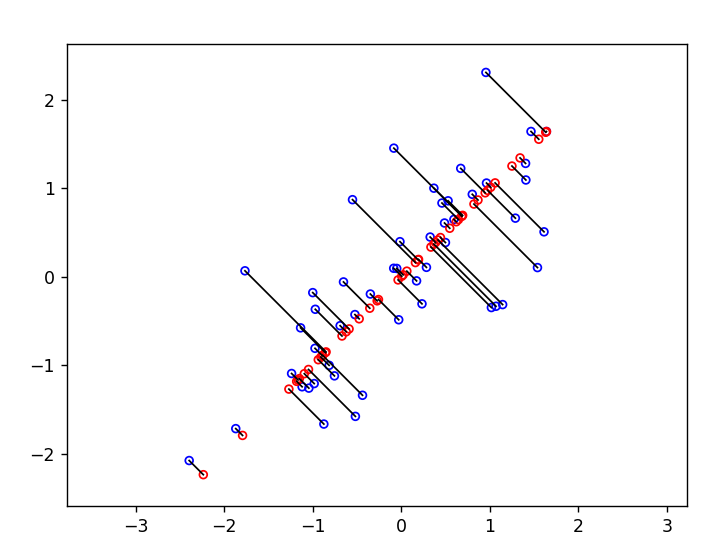
image-20231128091415842

导入面部数据

1
2
3
4
5
6
7
8
9
10
11
12
13
# ===================== 第4部分: 载入和可视化面部数据 =====================
# 首先加载和可视化数据集
print('加载面部数据集.')

# 加载面部数据集
data = scio.loadmat('ex7faces.mat')
X = data['X']

disp.display_data(X[0:100])

input('程序暂停。按回车键继续')


image-20231128091642007

面部数据PCA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# ===================== 第5部分: 在面部数据上运行PCA =====================
# 运行PCA并可视化结果，这里是特征脸
print('在面部数据集上运行PCA。\n(可能需要一两分钟...)')

# 在运行PCA之前，首先通过减去每个特征的均值来归一化X
X_norm, mu, sigma = fn.feature_normalize(X)

# 运行PCA
U, S = pca.pca(X_norm)

# 可视化前36个特征向量
disp.display_data(U[:, 0:36].T)

input('程序暂停。按回车键继续')

image-20231128091752689

面部数据降维

1
2
3
4
5
6
7
8
9
10
11
# ===================== 第6部分: 面部数据的降维 =====================
# 使用前k个特征向量将图像投影到特征空间
print('对面部数据进行降维.')

K = 100
Z = pd.project_data(X_norm, U, K)

print('投影数据Z的形状为: {}'.format(Z.shape))

input('程序暂停。按回车键继续')

可视化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# ===================== 第7部分: PCA降维后的面部可视化 =====================
# 将图像投影到特征空间的前K个特征向量，并仅使用这些K个维度进行可视化
print('可视化投影后（降维后）的面部图像.')

K = 100
X_rec = rd.recover_data(Z, U, K)

# 显示归一化数据
disp.display_data(X_norm[0:100])
plt.title('原始面部图像',fontproperties='SimHei')
plt.axis('equal')

# 显示仅使用k个特征向量重建的数据
disp.display_data(X_rec[0:100])
plt.title('恢复后的面部图像',fontproperties='SimHei')
plt.axis('equal')
plt.show()
input('程序暂停。按回车键继续')

image-20231128092247941

PCA可视化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# ===================== 第8(a)部分: 使用PCA进行可视化 =====================
# PCA的一个有用应用是用它来可视化高维数据。在上一个K-Means练习中，
# 在图像的3D像素颜色上运行K-Means。首先在3D中可视化这个输出，
# 然后应用PCA获得2D的可视化。

# 重新加载上一个练习中的图像并在其上运行K-Means
# 为了使其正常工作，您需要首先完成K-Means作业
image = io.imread('bird_small.png')
image = img_as_float(image)

img_shape = image.shape

X = image.reshape((img_shape[0] * img_shape[1], 3))
K = 16
max_iters = 10
initial_centroids = kmic.kmeans_init_centroids(X, K)
centroids, idx = km.run_kmeans(X, initial_centroids, max_iters, False)

# 随机选择1000个索引进行可视化
selected = np.random.randint(X.shape[0], size=1000)

# 在3D中可视化数据和质心成员关系
cm = plt.cm.get_cmap('RdYlBu')
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[selected, 0], X[selected, 1], X[selected, 2], c=idx[selected].astype(np.float64), s=15, cmap=cm, vmin=0, vmax=K)
plt.title('3D中绘制的像素数据集。颜色表示质心成员关系',fontproperties='SimHei')
plt.figure()
plt.show()
input('程序暂停。按回车键继续')

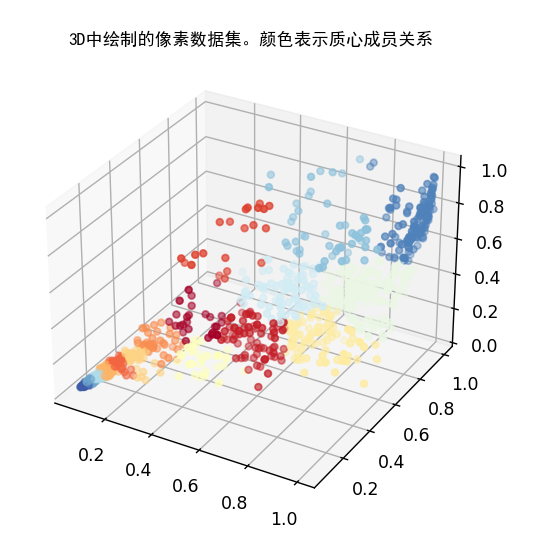
image-20231128092510688

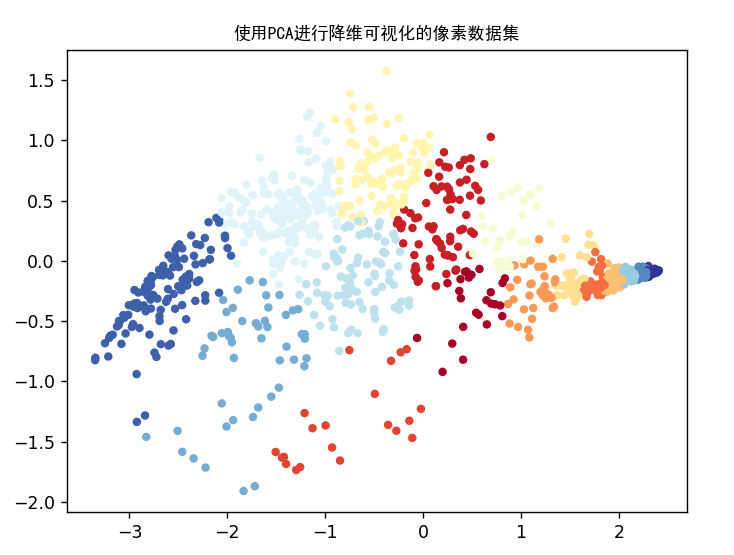
转为2D

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# ===================== 第8(b)部分: 使用PCA进行可视化 =====================
# 使用PCA将此点云投影到2D进行可视化

X_norm, mu, sigma = fn.feature_normalize(X)

# 运行PCA并将数据投影到2D
U, S = pca.pca(X_norm)
Z = pd.project_data(X_norm, U, 2)

# 在2D中绘制
plt.figure()
plt.scatter(Z[selected, 0], Z[selected, 1], c=idx[selected].astype(np.float64), s=15, cmap=cm)
plt.title('使用PCA进行降维可视化的像素数据集',fontproperties='SimHei')
plt.figure()
plt.show()
input('ex7_pca 完成。按回车键退出')

image-20231128092559613