无监督学习

简介

无监督学习是一种机器学习方法，其目标是从数据中发现模式、结构或关系，而不需要预先标记的目标变量。与监督学习不同，无监督学习不依赖于已知输出的训练数据。在无监督学习中，算法尝试从输入数据中提取信息，探索数据的内在结构，或者执行某种形式的聚类、降维、关联规则挖掘等任务。

聚类(Clustering): 将数据分成不同的组，使得同一组内的数据相似度较高，而不同组之间的相似度较低。
降维(Dimensionality Reduction): 减少数据的维度，保留最重要的特征，以便更好地理解数据或加速后续的学习算法。
异常检测(Anomaly Detection): 发现与大多数数据不同的异常数据点。
关联规则挖掘(Association Rule Mining): 寻找数据集中项目之间的关联关系，例如购物篮分析
生成模型(Generative Models): 学习数据的概率分布，以生成新的与训练数据相似的样本

聚类

定义

在一个典型的监督学习中，我们有一个有标签的训练集，我们的目标是找到能够区分正样本和负样本的决策边界，在这里的监督学习中，我们有一系列标签，我们需要据此拟合一个假设函数。与此不同的是，在非监督学习中，我们的数据没有附带任何标签，我们拿到的数据就是这样的：

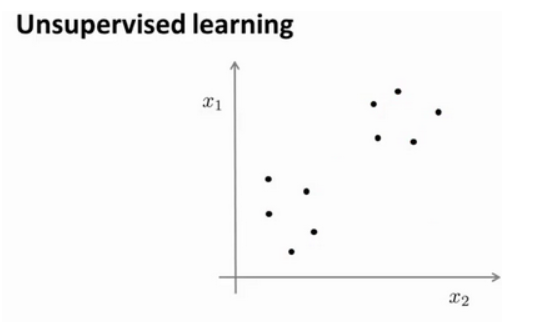
在这里有一系列点，却没有标签。因此，我们的训练集可以写成只有$x^{(1)}$,$x^{(2)}$…..一直到$x^{(m)}$。我们没有任何标签$y$。

我们可能需要某种算法帮助我们寻找一种结构。图上的数据看起来可以分成两个分开的点集（称为簇），一个能够找到我圈出的这些点集的算法，就被称为聚类算法。

聚类算法是一类无监督学习算法，其主要目标是将数据集中的样本分成不同的组，每个组内的样本相似度较高，而不同组之间的相似度较低。这样的分组通常称为簇（Cluster）。聚类算法旨在发现数据中的内在结构，帮助我们理解数据并进行有效的数据分析。

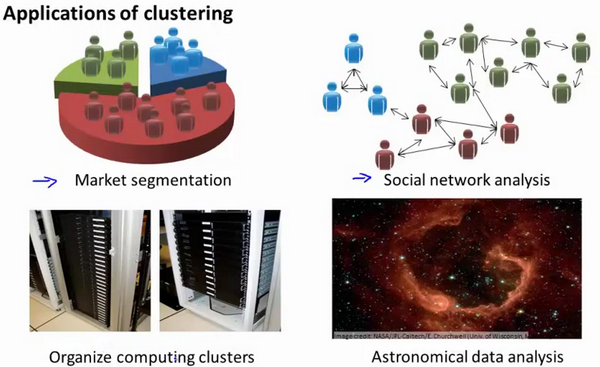
聚类算法可以应用到：市场分割，社交网络，计算机集群，天文数据分析等领域

K-均值算法

K均值聚类（K-Means Clustering）是一种常用的聚类算法，属于无监督学习的范畴。该算法的目标是将数据集划分成K个不同的簇，每个簇内的样本点与簇中心（cluster center）的距离最小。簇中心是簇内所有样本点的平均值

K-均值算法的步骤为：

选择簇的数量K： 首先，需要指定要形成的簇的数量$K$。
初始化簇中心： 随机选择$K$个样本作为初始簇中心，或者通过其他方法初始化。
分配样本到簇： 对每个样本，计算其与各个簇中心的距离，将样本分配给距离最近的簇。
更新簇中心： 对每个簇，计算簇内所有样本的平均值，将该平均值作为新的簇中心。
重复步骤3和步骤4： 重复执行分配样本到簇和更新簇中心的步骤，直到满足停止条件，例如簇中心不再发生显著变化或达到最大迭代次数。

下面是一个聚类示例：

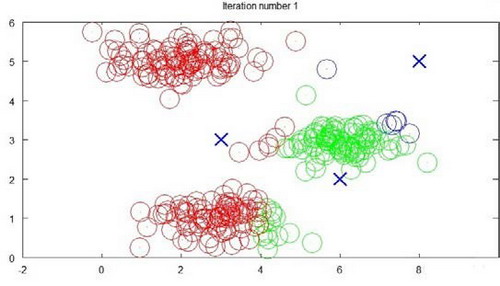
迭代 1 次

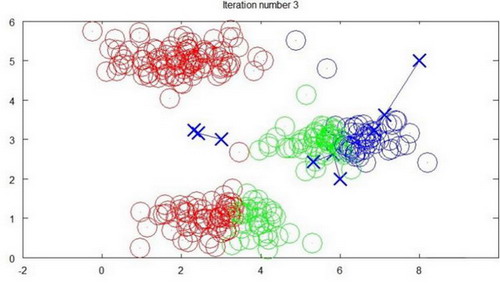
迭代 3 次

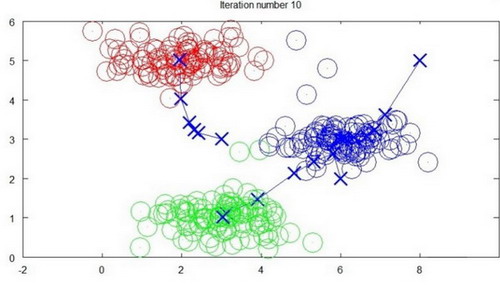
迭代 10 次

用$μ^1$,$μ^2$,…,$μ^k$ 来表示聚类中心，用$c^{(1)}$,$c^{(2)}$,…,$c^{(m)}$来存储与第$i$个实例数据最近的聚类中心的索引，K-均值算法的伪代码如下：

Repeat {

for i = 1 to m

c(i) := index (form 1 to K) of cluster centroid closest to x(i)

for k = 1 to K

μk := average (mean) of points assigned to cluster k

}

算法分为两个步骤，第一个for循环是赋值步骤，即：对于每一个样例$i$，计算其应该属于的类。第二个for循环是聚类中心的移动，即：对于每一个类$K$，重新计算该类的质心。

优化

K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此
K-均值的代价函数（又称畸变函数 Distortion function）为：

$J(c^{(1)}, \ldots, c^{(m)}, \mu_1, \ldots, \mu_K) = \frac{1}{m} \sum_{i=1}^{m} \|X^{(i)} - \mu_{c^{(i)}}\|^2$

其中$\mu_{c^{(i)}}$代表与$x^{(i)}$最近的聚类中心点。

我们的的优化目标便是找出使得代价函数最小的 $c^{(1)}$,$c^{(2)}$,…,$c^{(m)}$和$μ^1$,$μ^2$,…,$μ^k$，目标函数 ( $J$ ) 的含义是所有簇内样本点到其簇中心的距离平方和的总和。K均值聚类的优化目标就是找到一组簇中心，使得这个目标函数最小化。

K均值算法通过迭代执行两个步骤来优化这个目标：

簇分配步骤（Assign Step）： 将每个样本点分配给距离最近的簇中心。
簇更新步骤（Update Step）： 更新每个簇的中心，计算簇内所有样本的平均值。

这两个步骤交替进行，直到簇中心不再发生显著变化或达到最大迭代次数。在每次迭代后，目标函数 ( $J$ ) 都应该减小，这表示簇内样本点与簇中心之间的平方距离和在减小，从而更好地达到了聚类的效果。

随机初始化

运行K-均值算法的之前，我们首先要随机初始化所有的聚类中心点，下面介绍怎样做：

我们应该选择$K<m$，即聚类中心点的个数要小于所有训练集实例的数量
随机选择$K$个训练实例，然后令$K$个聚类中心分别与这$K$个训练实例相等

K-均值的一个问题在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情况。

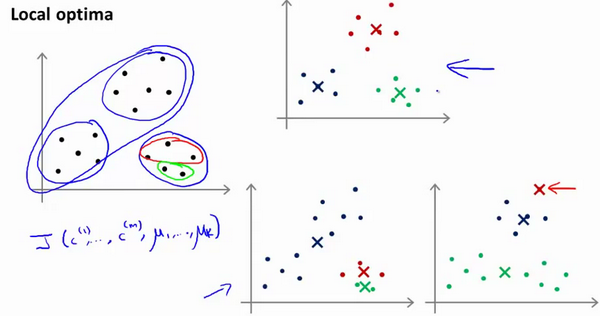
为了解决这个问题，我们通常需要多次运行**K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行K-均值**的结果，选择代价函数最小的结果。这种方法在$K$较小的时候（2—10）还是可行的，但是如果$K$较大，这么做也可能不会有明显地改善。

降维

数据压缩

降维：指通过减少数据的特征维度，从而保留数据关键信息的过程。在实际应用中，数据集往往包含大量的特征，而其中一些特征可能是冗余的、噪音的，或者不太重要的。通过降维，我们可以剔除这些不必要的信息，从而达到简化数据、提高模型性能的目的。

将数据从二维降至一维：

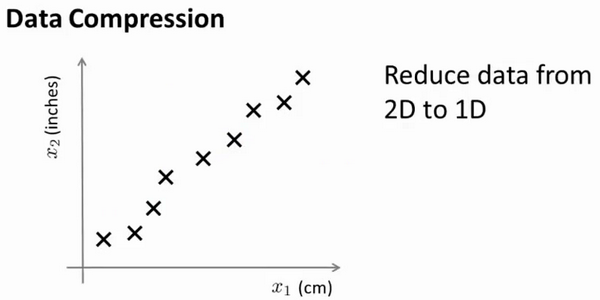
假设我们未知两个的特征：$x_1$:长度：用厘米表示；$x_2$：是用英寸表示同一物体的长度。

现在的问题的是，两种仪器对同一个东西测量的结果不完全相等（由于误差、精度等），而将两者都作为特征有些重复，因而，我们希望将这个二维的数据降至一维。

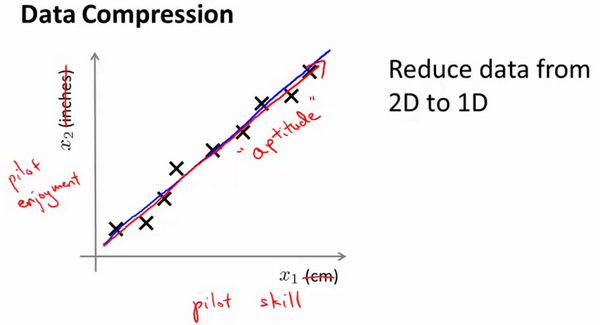
我们画出一条直线，降每个点都投影到直线上，观察投影点在直线上的位置，就将数据从二维降到了一维：

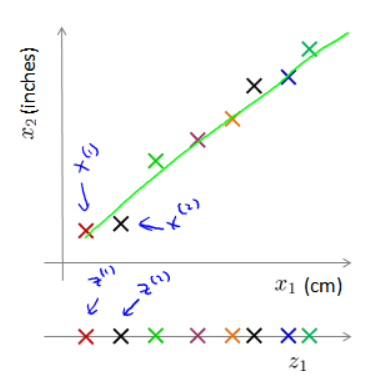
将数据从三维降至二维：

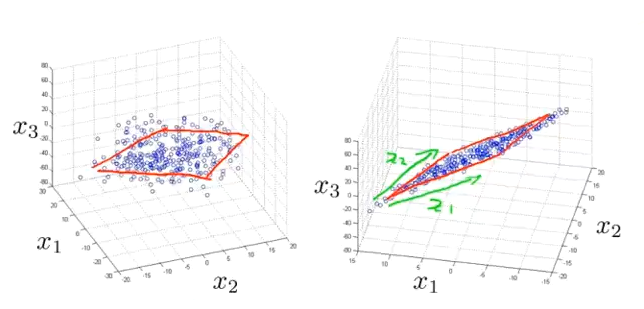
过程是与上面类似的，我们将三维向量投射到一个二维的平面上，强迫使得所有的数据都在同一个平面上，降至二维的特征向量。

这样的处理过程可以被用于把任何维度的数据降到任何想要的维度，例如将1000维的特征降至100维。

主成分分析(PCA)

主成分分析（Principal Component Analysis，PCA）是一种常用的降维技术，通过线性变换将原始数据映射到一个新的坐标系中，使得在新坐标系中数据的方差分布被最大化。这样，通过保留最重要的特征，PCA可以实现数据的降维。

在PCA中，我们要做的是找到一个方向向量（Vector direction），当我们把所有的数据都投射到该向量上时，我们希望投射平均均方误差能尽可能地小。方向向量是一个经过原点的向量，而投射误差是从特征向量向该方向向量作垂线的长度。

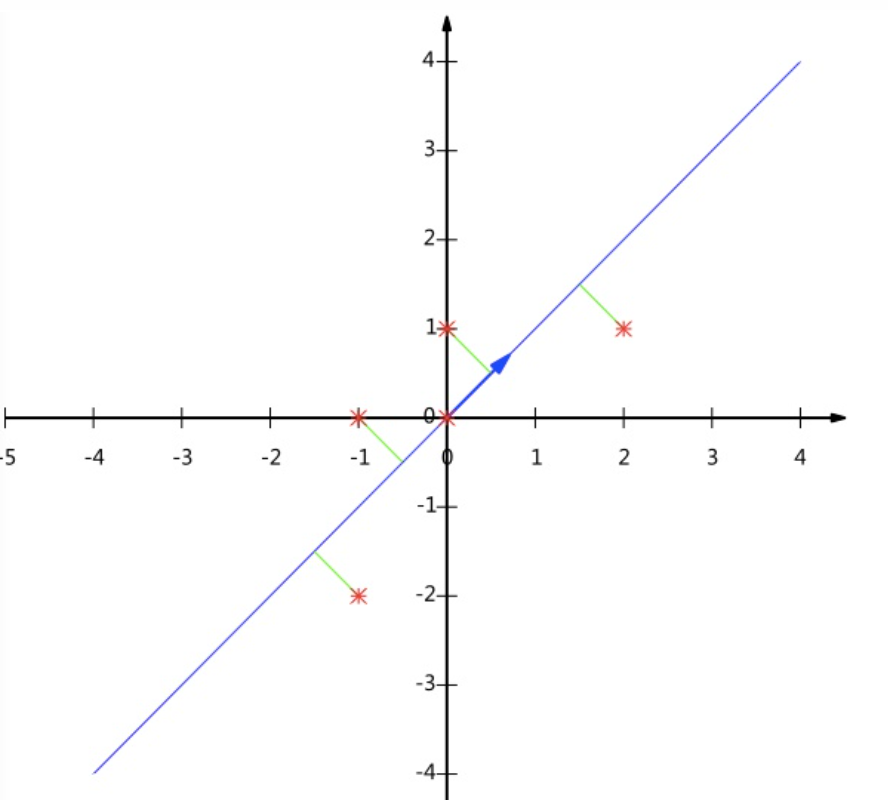
目标是找到向量$u^{(1)}$,$u^{(2)}$,…,$u^{(k)}$使得总的投射误差最小

主成分分析与线性回归是两种不同的算法。主成分分析最小化的是投射误差，而线性回归尝试的是最小化预测误差。线性回归的目的是预测结果，而主成分分析不作任何预测

算法

假设要利用PCA将数据从$n$维降低到$k$维

当执行主成分分析（PCA）时，具体的步骤可以如下：

均值归一化：
- 对每个特征减去该特征的均值，使得每个特征的均值为零。
其中，$(X)$ 是原始数据矩阵，$(\bar{X})$ 是每个特征的均值向量，。如果特征是在不同的数量级上，我们还需要将其除以标准差 $σ^2$
计算协方差矩阵：
- 计算中心化后的数据的协方差矩阵。
其中，($m$) 是样本数。
计算特征值和特征向量：
- 对协方差矩阵进行特征值分解。
其中，($\lambda$) 是特征值组成的对角矩阵，($V$) 是特征向量组成的矩阵。
选择主成分：
- 特征值表示数据在特征向量方向上的方差，选择特征值较大的前 ($k$) 个特征向量作为主成分。

构建投影矩阵：
- 将选择的主成分组成一个投影矩阵。
其中，$u^{(1)}$、$u^{(2)}$ 等是选择的主成分。对于一个 $n×n$维度的矩阵，上式中的$U$是一个具有与数据之间最小投射误差的方向向量构成的矩阵。如果我们希望将数据从$n$维降至$k$维，我们只需要从$U$中选取前$k$个向量，获得一个$n×k$维度的矩阵，我们用$U_{reduce}$表示
降维：
- 将原始数据乘以投影矩阵，将数据映射到新的低维空间。
其中$x$是$n×1$维的，因此结果为$k×1$维度。

这样，通过选择最重要的主成分，PCA实现了在保留尽可能多的信息的同时降低数据的维度。这对于减少特征的冗余性和去除噪声，以及在某些情况下提高模型性能都是有益的。

在Python中，使用U, S, V = scipy.linalg.svd(sigma)，sigma就是协方差矩阵Cov

$U$的列是$AA^T$的特征向量，称为左奇异向量。$S$是奇异值组成特征向量，$V$是右奇异向量矩阵$A^TA$的转置。你可以根据需要选择保留多少个主成分，例如，只取前$k$个奇异值对应的左右奇异向量，以实现降维。

选择主成分的数量

主要成分分析(PCA)的优化目标是减少投射的平均均方误差：

$\dfrac {1}{m}\sum^{m}_{i=1}\left\| x^{\left( i\right) }\right\| ^{2}$

我们希望在平均均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的$k$值。

如果我们希望这个比例小于1%，就意味着原本数据的偏差有99%都保留下来了，如果我们选择保留95%的偏差，便能非常显著地降低模型中特征的维度了。

可以通过特征矩阵来选择K，在python调用U, S, V = np.linalg.svd(sigma)中得到了S这个特征值数组，我们可以使用这个数组来计算平均均方误差与训练集方差的比例：

$\dfrac {\dfrac {1}{m}\sum^{m}_{i=1}\left\| x^{\left( i\right) }-x^{\left( i\right) }_{approx}\right\| ^{2}}{\dfrac {1}{m}\sum^{m}_{i=1}\left\| x^{(i)}\right\| ^{2}}=1-\dfrac {\Sigma^{k}_{i=1}S_{i}}{\Sigma^{m}_{i=1}S_{i}}\leq 1\%$

$i$慢慢减小，刚好满足条件的$i$，就是选择的$k$值

应用建议

一个常见错误使用主要成分分析的情况是，将其用于减少过拟合（减少了特征的数量）。这样做非常不好，不如尝试正则化处理。原因在于主要成分分析只是近似地丢弃掉一些特征，它并不考虑任何与结果变量有关的信息，因此可能会丢失非常重要的特征。然而当我们进行正则化处理时，会考虑到结果变量，不会丢掉重要的数据。

另一个常见的错误是，默认地将主要成分分析作为学习过程中的一部分，这虽然很多时候有效果，最好还是从所有原始特征开始，只在有必要的时候（算法运行太慢或者占用太多内存）才考虑采用主要成分分析。