推荐系统

简介

机器学习中的推荐系统是一种利用算法和模型来预测用户对特定项目的兴趣程度，并向用户推荐可能感兴趣的项目的系统。推荐系统在许多在线平台上都得到了广泛应用，例如电子商务网站、社交媒体平台、音乐和视频流媒体服务等。

推荐系统的主要目标是提供个性化的推荐，以提高用户体验，增加用户对平台的参与度，并帮助用户发现新的有趣内容。有两种主要类型的推荐系统：协同过滤和内容过滤。

从一个例子开始定义推荐系统的问题。

假使我们是一个电影供应商，我们有 5 部电影和 4 个用户，我们要求用户为电影打分。

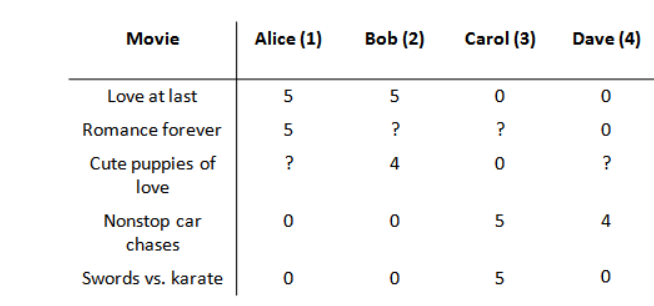
前三部电影是爱情片，后两部则是动作片，我们可以看出Alice和Bob似乎更倾向与爱情片，而 Carol 和 Dave 似乎更倾向与动作片。并且没有一个用户给所有的电影都打过分。我们希望构建一个算法来预测他们每个人可能会给他们没看过的电影打多少分，并以此作为推荐的依据。

下面引入一些标记：

$n_u$ 代表用户的数量
$n_m$ 代表电影的数量
$r(i, j)$ 如果用户j给电影 $i$ 评过分则 $r(i,j)=1$
$y^{(i, j)}$ 代表用户 $j$ 给电影$i$的评分
$m_j$代表用户 $j$ 评过分的电影的总数

内容过滤

这种方法利用项目的特征和用户的偏好之间的匹配来进行推荐。内容过滤系统会考虑项目的属性，例如关键词、主题或其他描述性特征，然后将这些特征与用户过去的行为或偏好进行匹配。

在一个基于内容的推荐系统算法中，我们假设对于我们希望推荐的东西有一些数据，这些数据是有关这些东西的特征。

在我们的例子中，我们可以假设每部电影都有两个特征，如$x_1$代表电影的浪漫程度，$x_2$ 代表电影的动作程度。

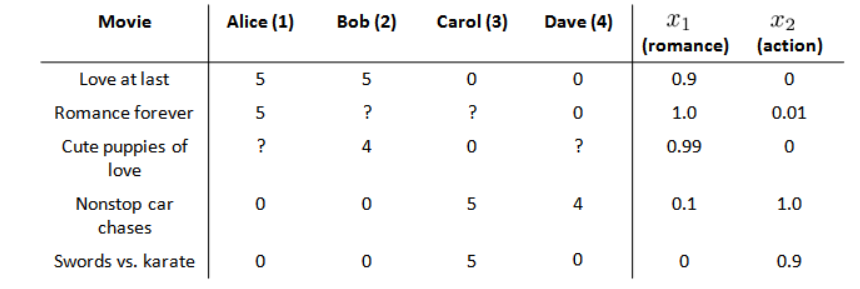
则每部电影都有一个特征向量，如$x^{(1)}$是第一部电影的特征向量为$[0.9,0]$

下面我们要基于这些特征来构建一个推荐系统算法。假设我们采用线性回归模型，我们可以针对每一个用户都训练一个线性回归模型，如$\theta ^{(1)}$是第一个用户的模型的参数。

于是，我们有：

$\theta^{(j)}$用户 $j$ 的参数向量
$x^{(i)}$电影 $i$ 的特征向量
对于用户 $j$ 和电影 $i$，我们预测评分为：$(\theta^{(j)})^T x^{(i)}$

比如alice是用户1，假设其$\theta^{(1)}=[0,5,0]$，而$x^{(3)}=[1,0.99,0]$，用$(\theta^{(1)})^T x^{(3)}=4.95$，所以预测其对第三部电影评分为4.95分

代价函数：针对用户 $j$，该线性回归模型的代价为预测误差的平方和，加上正则化项：

$\min_{\theta (j)}\frac{1}{2}\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2+\frac{\lambda}{2}\left(\theta_{k}^{(j)}\right)^2$

其中 $i:r(i,j)$表示我们只计算那些用户 $j$ 评过分的电影。在一般的线性回归模型中，误差项和正则项应该都是乘以$1/2m$，在这里我们将$m$去掉。并且我们不对方差项$\theta_0$进行正则化处理。

上面的代价函数只是针对一个用户的，为了学习所有用户，我们将所有用户的代价函数求和：

$\min_{\theta^{(1)},...,\theta^{(n_u)}} \frac{1}{2}\sum_{j=1}^{n_u}\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2$

用梯度下降法求最优解：

$\theta_k^{(j)}:=\theta_k^{(j)}-\alpha\left(\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x_{k}^{(i)}+\lambda\theta_k^{(j)}\right) \quad (\text{for} \, k\neq 0)$

协同过滤

定义：协同过滤是推荐系统中一种常见的技术，它基于用户之间的相似性或项目之间的相似性来进行推荐。这种方法利用用户和项目的历史行为或偏好信息，通过比较用户或项目之间的相似性，预测用户可能感兴趣的项目或向用户推荐可能喜欢的其他用户。

在之前的基于内容的推荐系统中，对于每一部电影，我们都掌握了可用的特征，使用这些特征训练出了每一个用户的参数。相反地，如果我们拥有用户的参数，我们可以学习得出电影的特征

$\mathop{min}\limits_{x^{(1)},...,x^{(n_m)}}\frac{1}{2}\sum_{i=1}^{n_m}\sum_{j{r(i,j)=1}}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_k^{(i)})^2$

但是如果我们既没有用户的参数，也没有电影的特征，这两种方法都不可行了，而协同过滤算法可以同时学习这两者。

我们的优化目标便改为同时针对$x$和$\theta$进行。

$J(x^{(1)},...x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)})=\frac{1}{2}\sum_{(i:j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_k^{(j)})^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2$

对代价函数求偏导数的结果如下：

$x_k^{(i)}:=x_k^{(i)}-\alpha\left(\sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\theta_k^{j}+\lambda x_k^{(i)}\right)$ $\theta_k^{(i)}:=\theta_k^{(i)}-\alpha\left(\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}x_k^{(i)}+\lambda \theta_k^{(j)}\right)$

注：在协同过滤从算法中，我们通常不使用$x_0=1$的截距项，如果需要的话，算法会自动学得。

协同过滤算法使用步骤如下：

初始 $x^{(1)},x^{(1)},…x^{(nm)},\ \theta^{(1)},\theta^{(2)},…,\theta^{(n_u)}$为一些随机小值
使用梯度下降算法最小化代价函数
在训练完算法后，我们预测$(\theta^{(j)})^Tx^{(i)}$为用户 $j$ 给电影 $i$ 的评分

通过这个学习过程获得的特征矩阵包含了有关电影的重要数据，这些数据不总是人能读懂的，但是我们可以用这些数据作为给用户推荐电影的依据。

例如，如果一位用户正在观看电影 $x^{(i)}$，我们可以寻找另一部电影$x^{(j)}$，依据两部电影的特征向量之间的距离$\left| {x}^{(i)}-{x}^{(j)} \right|$的大小。

低秩矩阵分解

低秩矩阵分解（Low Rank Matrix Factorization）是一种矩阵分解技术，常被应用于推荐系统和数据降维等领域。其核心思想是将一个大矩阵表示为两个或多个较小维度的矩阵的乘积，这些小矩阵通常被称为因子矩阵。低秩表示意味着这些因子矩阵的秩（rank）相对较小。

在推荐系统中，低秩矩阵分解主要用于学习用户和物品之间的潜在关系。通过将用户-物品评分矩阵分解为用户因子矩阵和物品因子矩阵，可以学习到用户和物品的隐藏特征，从而进行个性化的推荐。

举例说明：

我们有关于五部电影的数据集，我将要做的是，将这些用户的电影评分，进行分组并存到一个矩阵中。

我们有五部电影，以及四位用户，那么这个矩阵 $Y$ 就是一个5行4列的矩阵，它将这些电影的用户评分数据都存在矩阵里：

Movie	Alice (1)	Bob (2)	Carol (3)	Dave (4)
Love at last	5	5	0	0
Romance forever	5	?	?	0
Cute puppies of love	?	4	0	?
Nonstop car chases	0	0	5	4
Swords vs. karate	0	0	5	?

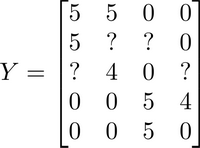
那么用户-物品评分矩阵可以表示为：

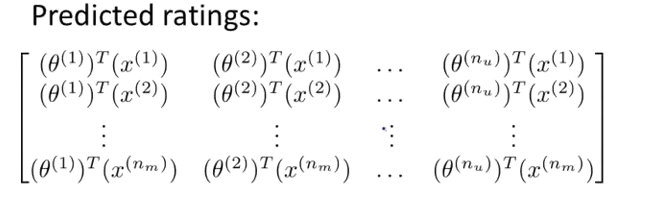
这矩阵可以被分解为物品因子矩阵和用户因子矩阵，分别是：$X=\left [ \begin{matrix}
x^{(1)} \\
x^{(2)}\\
\cdot\cdot\cdot\\
x^{(n)}\\
\end{matrix} \right ]$以及$\Theta=\left [ \begin{matrix}
\theta^{(1)^T} \\
\theta^{(2)^T}\\
\cdot\cdot\cdot\\
\theta^{(n)^T}\\
\end{matrix} \right ]$

其中，$X$的每一行表示一个物品的潜在特征，$\Theta$的每一行表示一个用户的潜在特征。矩阵$\Theta^T X$的乘积近似等于原始评分矩阵

低秩矩阵分解的优点之一是它能够处理数据的稀疏性，即使用户只对很少的物品进行了评分，也能够进行有效的推荐。此外，低秩矩阵分解还可以通过学习潜在特征来发现用户和物品之间的关系，从而提高推荐的准确性。

均值归一化

让我们来看下面的用户评分数据：

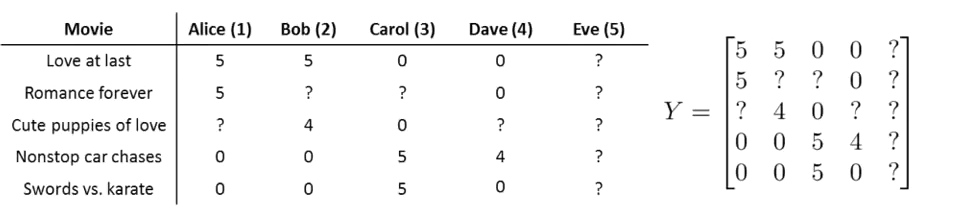
如果我们新增一个用户 Eve，并且 Eve 没有为任何电影评分，那么我们以什么为依据为Eve推荐电影呢？

直接用协同过滤计算，结果会是Eve对电影的评分都为0，这样无法给eve推荐

我们首先需要对结果 $Y $矩阵进行均值归一化处理，将每一个用户对某一部电影的评分减去所有用户对该电影评分的平均值：

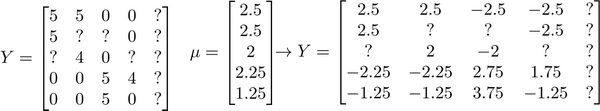
然后我们利用这个新的 $Y$ 矩阵来训练算法。
如果我们要用新训练出的算法来预测评分，则需要将平均值重新加回去，预测$(\theta^{(j)})^T x^{(i)}+\mu_i$，对于Eve，我们的新模型会认为她给每部电影的评分都是该电影的平均分。