ex8:anomaly detection and recommendation

异常检测

概述

在这个练习中，您将实现异常检测算法并将其应用于检测网络上的故障服务器

必要的文件：

  • ex8.py - 用于练习第一部分的Python脚本
  • ex8data1.mat - 用于异常检测的第一个示例数据集
  • ex8data2.mat - 用于异常检测的第二个示例数据集
  • multivariateGaussian.py - 计算高斯分布的概率密度函数
  • visualizeFit.py - 高斯分布和数据集的二维图

需要补充的文件：

  • estimateGaussian.py - 估算带有对角协方差矩阵的高斯分布的参数
  • selectThreshold.py - 为异常检测找到阈值

导入

1
2
3
4
5
6
7
8
9
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as scio

# 导入自定义模块
import estimateGaussian as eg
import multivariateGaussian as mvg
import visualizeFit as vf
import selectThreshold as st

载入并绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# ===================== 第 1 部分：加载示例数据集 =====================
# 通过使用一个小型易于可视化的数据集开始本练习。
#
# 我们的示例案例包括多台机器上两个网络服务器统计信息：
# 每台机器的延迟和吞吐量。这个练习将帮助我们找到可能存在故障（或非常快速）的机器

print('正在可视化用于异常检测的示例数据集.')

# 以下命令加载数据集。现在，您的环境中应该有变量X、Xval、yval。
data = scio.loadmat('ex8data1.mat')
X = data['X']
Xval = data['Xval']
yval = data['yval'].flatten()

# 可视化示例数据集
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c='b', marker='x', s=15, linewidth=1)
plt.axis([0, 30, 0, 30])
plt.xlabel('延迟（ms）',fontproperties='SimHei')
plt.ylabel('吞吐量（mb/s）',fontproperties='SimHei')
plt.show()
input('程序暂停。按回车键继续')

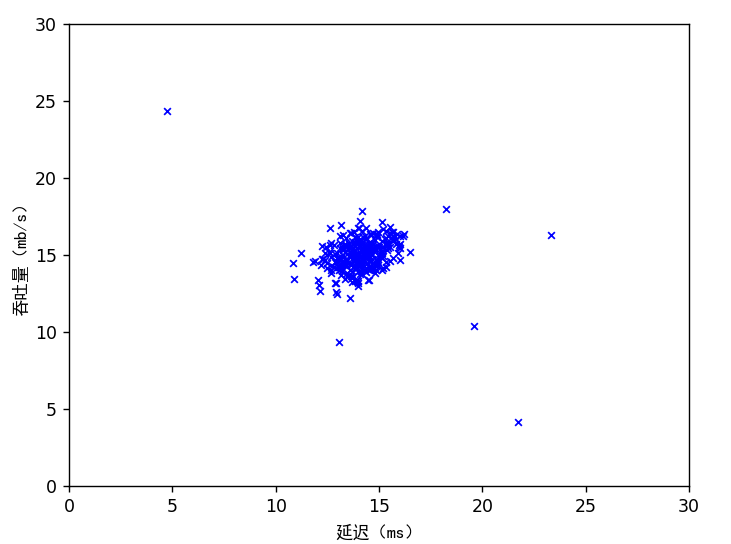
image-20231201014157144

高斯拟合

首先编写高斯拟合的python文件：estimateGaussian.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np

def estimate_gaussian(X):
    # 有用的变量
    m, n = X.shape

    # 你应该正确返回这些值
    mu = np.zeros(n)
    sigma2 = np.zeros(n)

    # ===================== 你的代码在这里 =====================
    # 说明: 计算数据的均值和方差
    #      具体来说，mu[i] 应该包含第 i 个特征的均值，
    #      sigma2[i] 应该包含第 i 个特征的方差
    #
    for i in range(n):
        mu[i]=np.sum(X[:,i])/m
        sigma2[i]=np.sum((X[:,i]-mu[i])**2)/m

    # ==========================================================

    return mu, sigma2

找到$\sigma$和$\mu^2$，然后代入已经写好的multivariate_gaussian函数中，直接算出概率p

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# ===================== 第 2 部分：估算数据集统计信息 =====================
# 对于本练习，我们假设数据集服从高斯分布。
#
# 首先估算我们假设的高斯分布的参数，
# 然后计算每个点的概率，然后可视化
# 整体分布以及每个点在该分布中的位置

print('正在可视化高斯拟合.')

# 估算 mu 和 sigma2
mu, sigma2 = eg.estimate_gaussian(X)

# 返回X中每个数据点（行）的多元正态分布密度
p = mvg.multivariate_gaussian(X, mu, sigma2)

# 可视化拟合
vf.visualize_fit(X, mu, sigma2)
plt.xlabel('延迟（ms）',fontproperties='SimHei')
plt.ylabel('吞吐量（mb/s）',fontproperties='SimHei')

input('程序暂停。按回车键继续')

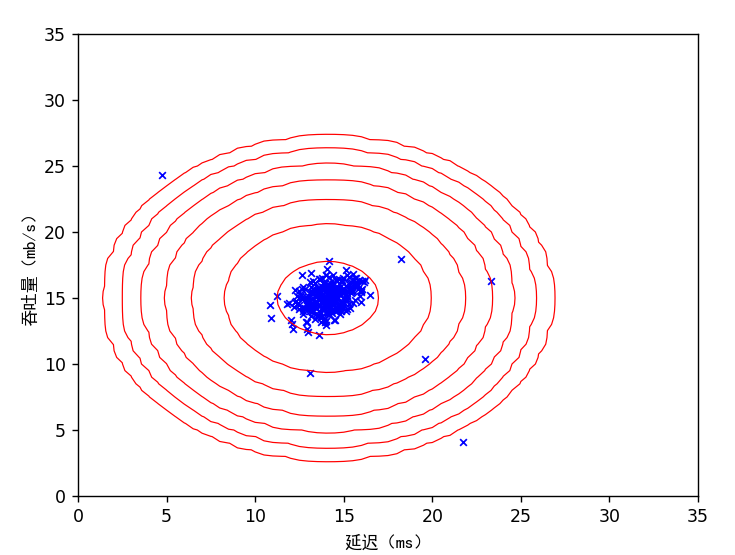
image-20231201014619751

查找异常值

完成selectThreshold.py函数，根据概率pval和真实值yval，找出最佳的$\epsilon$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import numpy as np

def select_threshold(yval, pval):
    f1 = 0

    # 你必须正确返回这些值
    best_eps = 0
    best_f1 = 0

    for epsilon in np.linspace(np.min(pval), np.max(pval), num=1001):
        # ===================== 你的代码在这里 =====================
        # 说明: 计算选择 epsilon 作为阈值的 F1 分数，并将值放入 F1。
        #       循环结束时，代码将比较此 epsilon 选择的 F1 分数，
        #       如果它优于当前选择的 epsilon，则将其设置为最佳 epsilon。
        #
        # 注意: 您可以使用 predictions = pval < epsilon 来获取二进制向量，
        #       其中 False(0) 表示非异常值，True(1) 表示异常值
        #
        # 计算真正例（True Positives）
        tp = np.sum((yval == 1) & (pval < epsilon))

        # 计算假正例（False Positives）
        fp = np.sum((yval == 0) & (pval < epsilon))

        # 计算假负例（False Negatives）
        fn = np.sum((yval == 1) & (pval >= epsilon))

        # 计算精确度（Precision）和召回率（Recall）
        precision = tp / (tp + fp) if (tp + fp) > 0 else 0
        recall = tp / (tp + fn) if (tp + fn) > 0 else 0

        # 计算 F1 分数
        f1 = 2 * precision * recall / (precision + recall) if (precision + recall) > 0 else 0

        # ==========================================================

        if f1 > best_f1:
            best_f1 = f1
            best_eps = epsilon

    return best_eps, best_f1

直接用np.sum((yval == 1) & (pval < epsilon))的语法，让两个布尔数组进行与操作，然后相加，就可以得到真正例tp，非常精妙

回到ex8.py中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# ===================== 第 3 部分：查找异常值 =====================
# 现在，您将使用交叉验证集找到一个合适的 epsilon 阈值，
# 给定估算的高斯分布的概率

pval = mvg.multivariate_gaussian(Xval, mu, sigma2)

epsilon, f1 = st.select_threshold(yval, pval)
print('使用交叉验证找到的最佳 epsilon 值：{:0.4e}'.format(epsilon))
print('交叉验证集上的最佳 F1 值：{:0.6f}'.format(f1))
print('(您应该看到 epsilon 约为 8.99e-05，F1 约为 0.875)')

# 在训练集中找到并绘制异常值
outliers = np.where(p < epsilon)
plt.scatter(X[outliers, 0], X[outliers, 1], marker='o', facecolors='none', edgecolors='r')
plt.show()
input('程序暂停。按回车键继续')

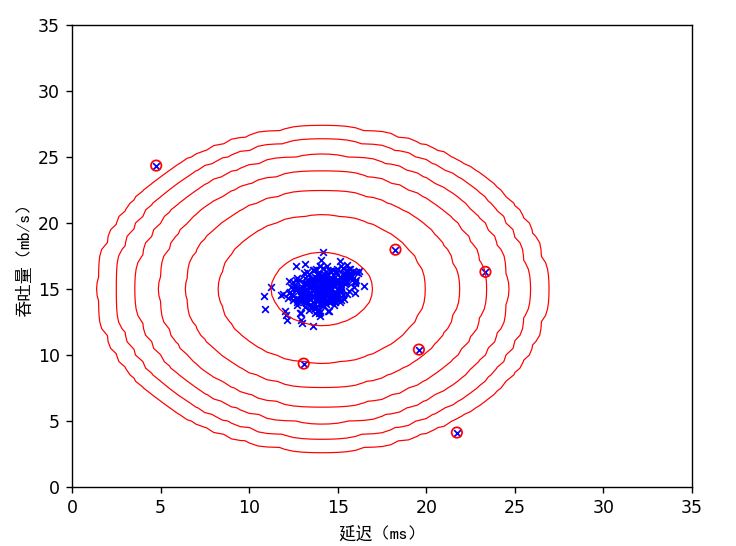
image-20231201015032314

测试

最后使用之前写的代码，代入数据集2中进行测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# ===================== 第 4 部分：多维异常值 =====================
# 现在，我们将使用前一部分的代码并将其应用于一个更难的问题，
# 其中更多的特征描述每个数据点，只有一些特征指示一个点是否是异常值。

# 加载第二个数据集。
data = scio.loadmat('ex8data2.mat')
X = data['X']
Xval = data['Xval']
yval = data['yval'].flatten()

# 对较大的数据集应用相同的步骤
mu, sigma2 = eg.estimate_gaussian(X)

# 训练集
p = mvg.multivariate_gaussian(X, mu, sigma2)

# 交叉验证集
pval = mvg.multivariate_gaussian(Xval, mu, sigma2)

# 找到最佳阈值
epsilon, f1 = st.select_threshold(yval, pval)

print('使用交叉验证找到的最佳 epsilon 值：{:0.4e}'.format(epsilon))
print('交叉验证集上的最佳 F1 值：{:0.6f}'.format(f1))
print('发现的异常值数量：{}'.format(np.sum(np.less(p, epsilon))))
print('(您应该看到 epsilon 约为 1.38e-18，F1 约为 0.615，以及 117 个异常值)')

input('ex8 完成。按回车键退出')

np.less(p, epsilon): 这部分代码使用NumPy库中的np.less()函数，它会逐元素比较数组p中的每个元素是否小于epsilon。这将生成一个布尔值的数组，其中True表示对应位置的元素小于epsilon，False表示大于或等于epsilon。

推荐系统

概述

在第二部分中，您将使用协同过滤构建电影推荐系统

必要的文件：

  • ex8_cofi.py - 用于练习第二部分的Python脚本
  • ex8 movies.mat - 电影评论数据集
  • ex8 movieParams.mat - 用于调试的参数
  • checkCostFunction.py - 协同过滤的梯度
  • loadMovieList.py - 将电影列表加载到单元数组中
  • movie_ids.txt - 电影列表
  • normalizeRatings.py - 协同过滤的均值归一化
  • computeNumericalGradient.py - 数值计算梯度

需要补充的文件：

  • cofiCostFunc.py - 实现协同过滤的成本函数

导入

1
2
3
4
5
6
7
8
9
10
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as scio
import scipy.optimize as opt

# 导入自定义模块
import cofiCostFunction as ccf
import checkCostFunction as cf
import loadMovieList as lm
import normalizeRatings as nr

载入并绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# ===================== 第 1 部分：加载电影评分数据集 =====================
# 我们将首先加载电影评分数据集，以了解数据的结构
print('加载电影评分数据集.')

# 加载数据
data = scio.loadmat('ex8_movies.mat')
Y = data['Y']
R = data['R']

# Y 是一个 1682 x 943 的 2 维 ndarray，包含 1682 部电影在 943 个用户上的评分（1-5）
#
# R 是一个 1682 x 943 的 2 维 ndarray，其中 R[i, j] = 1 当且仅当用户 j 给电影 i 打了分
#

# 从矩阵中，我们可以计算出诸如平均评分之类的统计信息。
print('电影 0（Toy Story）的平均评分: {:0.6f}/5'.format(np.mean(Y[0, np.where(R[0] == 1)])))

# 我们可以通过使用 plt.imshow 来可视化评分矩阵
plt.figure()
plt.imshow(Y)
plt.colorbar()
plt.xlabel('用户',fontproperties='SimHei')
plt.ylabel('电影',fontproperties='SimHei')
plt.show()
input('程序暂停。按回车键继续')

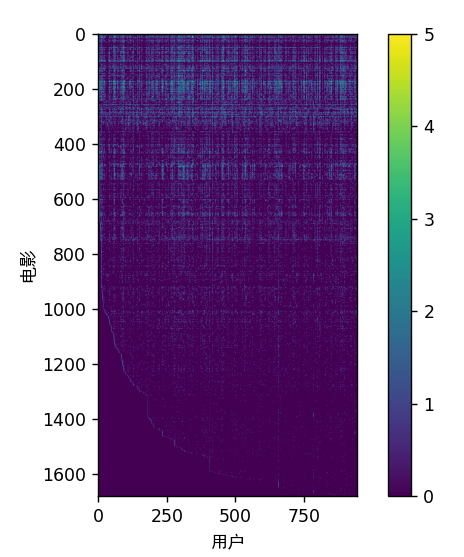
image-20231201030452789

成本函数

需要完成成本函数cofiCostFunc.py文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import numpy as np

def cofi_cost_function(params, Y, R, num_users, num_movies, num_features, lmd):
    X = params[0:num_movies * num_features].reshape((num_movies, num_features))
    theta = params[num_movies * num_features:].reshape((num_users, num_features))

    # 你需要正确设置以下值。
    cost = 0
    X_grad = np.zeros(X.shape)
    theta_grad = np.zeros(theta.shape)

    # ===================== 你的代码在这里 =====================
    # 说明: 计算协同过滤的成本函数和梯度。
    # 具体来说，你应该首先实现成本函数（不带正则化），并确保它匹配我们的成本。
    # 之后，你应该实现梯度并使用 checkCostFunction 例程来检查梯度是否正确。
    # 最后，你应该实现正则化。
    #
    # 注意:   X - num_movies x num_features 的电影特征矩阵
    #        theta - num_users x num_features 的用户特征矩阵
    #        Y - num_movies x num_users 的用户对电影的评分矩阵
    #        R - num_movies x num_users 矩阵，其中 R[i, j] = 1 表示第 i 部电影被第 j 个用户评分
    #
    # 你应该正确设置以下变量
    #
    #        X_grad - num_movies x num_features 的矩阵，包含对 X 的每个元素的偏导数
    #        theta_grad - num_users x num_features 的矩阵，包含对 theta 的每个元素的偏导数
    error = (X @ theta.T - Y) * R
    cost = 0.5 * np.sum(error ** 2) + 0.5 * lmd * (np.sum(theta ** 2) + np.sum(X ** 2))

    # 计算 X_grad 和 theta_grad
    X_grad = error @ theta + lmd * X
    theta_grad = error.T @ X + lmd * theta


    # ==========================================================

    grad = np.concatenate((X_grad.flatten(), theta_grad.flatten()))

    return cost, grad

回到ex8_cofi.py文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# ===================== 第 2 部分：协同过滤成本函数 =====================
# 现在，你将实现协同过滤的成本函数。
# 为了帮助你调试成本函数，我们已经提供了我们在其上训练的一组权重。
# 具体来说，你应该在 cofiCostFunc.py 中完成代码以返回成本。
#

# 加载预先训练的权重（X、theta、num_users、num_movies、num_features）
data = scio.loadmat('ex8_movieParams.mat')
X = data['X']
theta = data['Theta']
num_users = data['num_users']
num_movies = data['num_movies']
num_features = data['num_features']

# 减小数据集的大小以加快运行速度
num_users = 4
num_movies = 5
num_features = 3
X = X[0:num_movies, 0:num_features]
theta = theta[0:num_users, 0:num_features]
Y = Y[0:num_movies, 0:num_users]
R = R[0:num_movies, 0:num_users]

# 计算成本函数
cost, grad = ccf.cofi_cost_function(np.concatenate((X.flatten(), theta.flatten())), Y, R, num_users, num_movies, num_features, 0)

print('加载参数的成本: {:0.2f}\n(这个值应该约为 22.22)'.format(cost))

input('程序暂停。按回车键继续')

正则化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# ===================== 第 4 部分：协同过滤成本正则化 =====================
# 现在，你应该为协同过滤的成本函数实现正则化。
# 你可以通过将正则化的成本添加到原始成本计算中来实现它。
#

# 计算成本函数
cost, _ = ccf.cofi_cost_function(np.concatenate((X.flatten(), theta.flatten())), Y, R, num_users, num_movies, num_features, 1.5)

print('加载参数的成本（lambda = 1.5）: {:0.2f}\n'
      '(这个值应该约为 31.34)'.format(cost))

input('程序暂停。按回车键继续')

# ===================== 第 5 部分：协同过滤梯度正则化 =====================
# 一旦你的成本与我们的匹配，你应该继续实现梯度的正则化。
#

print('检查梯度（带正则化）...')

# 通过运行 check_cost_function 来检查梯度
cf.check_cost_function(1.5)

input('程序暂停。按回车键继续')

新用户打分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# ===================== 第 6 部分：为新用户输入评分 =====================
# 在训练协同过滤模型之前，我们将首先添加与我们刚观察到的新用户相对应的评分。
# 代码的这一部分还将允许你为数据集中的电影输入你自己的评分！
#
movie_list = lm.load_movie_list()

# 初始化我的评分
my_ratings = np.zeros(len(movie_list))

# 检查文件 movie_ids.txt 获取我们数据集中每部电影的 id
# 例如，Toy Story (1995) 的 ID 为 0，所以要给它评分 "4"，你可以设置
my_ratings[0] = 4

# 或者假设不喜欢 Silence of the Lambs (1991)，你可以设置
my_ratings[97] = 2

# 我们已经选择了一些我们喜欢/不喜欢的电影，我们给出的评分如下：
my_ratings[6] = 3
my_ratings[11] = 5
my_ratings[53] = 4
my_ratings[63] = 5
my_ratings[65] = 3
my_ratings[68] = 5
my_ratings[182] = 4
my_ratings[225] = 5
my_ratings[354] = 5

print('新用户的评分:\n')
for i in range(my_ratings.size):
    if my_ratings[i] > 0:
        print('对 {} 评分为 {}'.format(movie_list[i], my_ratings[i]))

input('程序暂停。按回车键继续')

学习评分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
# ===================== 第 7 部分：学习电影评分 =====================
# 现在，你将在包含 1682 部电影和 943 个用户的电影评分数据集上训练协同过滤模型
#
print('训练协同过滤...\n'
      '(这可能需要 1 ~ 2 分钟)')


# 加载数据
data = scio.loadmat('ex8_movies.mat')
Y = data['Y']
R = data['R']

# Y 是一个 1682x943 的矩阵，包含 943 个用户对 1682 部电影的评分（1-5）
#
# R 是一个 1682x943 的矩阵，其中 R[i,j] = 1 当且仅当用户 j 给电影 i 打了分

# 将我们自己的评分添加到数据矩阵中
Y = np.c_[my_ratings, Y]
R = np.c_[(my_ratings != 0), R]

# 规范化评分
Ynorm, Ymean = nr.normalize_ratings(Y, R)

# 有用的值
num_users = Y.shape[1]
num_movies = Y.shape[0]
num_features = 10

# 设置初始参数（theta、X）
X = np.random.randn(num_movies, num_features)
theta = np.random.randn(num_users, num_features)

initial_params = np.concatenate([X.flatten(), theta.flatten()])

lmd = 10


def cost_func(p):
    return ccf.cofi_cost_function(p, Ynorm, R, num_users, num_movies, num_features, lmd)[0]


def grad_func(p):
    return ccf.cofi_cost_function(p, Ynorm, R, num_users, num_movies, num_features, lmd)[1]

theta, *unused = opt.fmin_cg(cost_func, fprime=grad_func, x0=initial_params, maxiter=100, disp=False, full_output=True)

# 将返回的 theta 展开回 U 和 W
X = theta[0:num_movies * num_features].reshape((num_movies, num_features))
theta = theta[num_movies * num_features:].reshape((num_users, num_features))

print('推荐系统学习完成')
print(theta)

input('程序暂停。按回车键继续')

推荐电影

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# ===================== 第 8 部分：为你推荐 =====================
# 在训练模型之后，你现在可以通过计算预测矩阵来进行推荐。
#
p = np.dot(X, theta.T)
my_predictions = p[:, 0] + Ymean

indices = np.argsort(my_predictions)[::-1]
print('\n为你推荐的前 10 部电影:')
for i in range(10):
    j = indices[i]
    print('预测评分 {:0.1f} 给电影 {}'.format(my_predictions[j], movie_list[j]))

print('\n原始评分:')
for i in range(my_ratings.size):
    if my_ratings[i] > 0:
        print('对 {} 评分为 {}'.format(movie_list[i], my_ratings[i]))

input('ex8_cofi 完成。按回车键退出')