大规模机器学习

概念

大规模的机器学习（Large-Scale Machine Learning）指的是在处理庞大规模数据集或在复杂模型中应用机器学习算法的领域。这涉及到处理大量的样本、特征和/或模型参数，通常需要高度并行化、分布式计算和优化算法以应对计算和存储的挑战。

如果我们有一个低方差的模型，增加数据集的规模可以帮助你获得更好的结果。我们应该怎样应对一个有1000万条记录的训练集？

以线性回归模型为例，每一次梯度下降迭代，我们都需要计算训练集的误差的平方和，如果我们的学习算法需要有20次迭代，这便已经是非常大的计算代价。

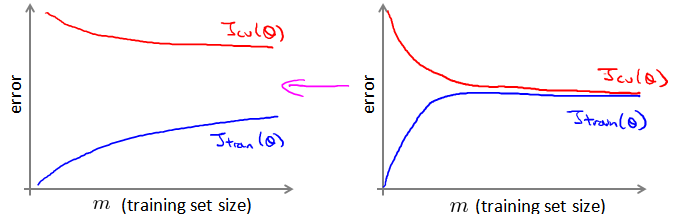
首先应该做的事是去检查一个这么大规模的训练集是否真的必要，也许我们只用1000个训练集也能获得较好的效果，我们可以绘制学习曲线来帮助判断。

随机梯度下降

如果我们一定需要一个大规模的训练集，我们可以尝试使用随机梯度下降法来代替批量梯度下降法。

随机梯度下降是一种优化算法，用于训练机器学习模型，特别是在大规模数据集上。与批量梯度下降（Batch Gradient Descent）一次性使用整个训练集的所有样本相比，SGD每次迭代只使用一个随机选择的样本来计算梯度和更新模型参数

SGD的主要思想是通过随机选择一个样本来估计整个训练数据的梯度，然后利用该梯度来更新模型参数。这样的更新是基于单个样本的，因此计算速度相对较快。然而，由于每次迭代的梯度估计都是基于单个样本的，导致参数的更新比较嘈杂，使得收敛路径较为不规律。

在随机梯度下降法中，我们定义代价函数为一个单一训练实例的代价：

$cost( \theta, ( {x}^{(i)} , {y}^{(i)} ) ) = \frac{1}{2}\left( {h}_{\theta}({x}^{(i)}\right)-{y}^ )^{2}$

随机梯度下降算法为：首先对训练集随机“洗牌”，然后：

$\theta_{i+1} = \theta_i - \alpha \left(h_{\theta}\left(x^{(i)}\right)-{y}^{(i)} \right){x_j}^{(i)}$

其中：

($\theta_i$) 是第 ($i$) 次迭代后的模型参数。
($\alpha$) 是学习率，控制每次迭代中参数更新的步长。
($J(\theta_i; x^{(i)}, y^{(i)})$) 是损失函数，表示模型在样本 ($x^{(i)}$) 上的损失。

SGD的主要优势在于它能够处理大规模数据集，因为每次迭代只需要处理一个样本。此外，SGD的更新过程对于在线学习是很有用的，模型可以逐步地适应新的数据。

然而，由于更新的不规律性，SGD可能会在接近最优解时震荡，甚至可能略过最优解。为了解决这个问题，通常会采用一些变种，如小批量梯度下降，它每次迭代使用一个小的样本集合来估计梯度，从而在计算效率和更新稳定性之间取得一种平衡。

小批量梯度下降

小批量梯度下降（Mini-Batch Gradient Descent）是梯度下降算法的一种变种，它介于随机梯度下降（SGD）和批量梯度下降（Batch GD）之间。在小批量梯度下降中，每次迭代不再使用整个训练数据集，而是随机选择一个小的样本集合（称为”小批量”或”mini-batch”），然后使用这个小批量来计算梯度和更新模型参数

每计算常数$b$次训练实例，便更新一次参数 $$ 。

Repeat {

for $i = 1:m${

$\theta:={\theta}_j-\alpha\frac{1}{b}\sum_\limits{k=i}^{i+b-1}\left( h_{\theta}\left(x^{(k)}\right)-{y}^{(k)} \right){x_j}^{(k)}$

(for $j=0:n$)

$ i +=10 $

}
}

通常我们会令 $b$ 在 2-100 之间。这样做的好处在于，我们可以用向量化的方式来循环 $b$个训练实例，如果我们用的线性代数函数库比较好，能够支持平行处理，那么算法的总体表现将不受影响（与随机梯度下降相同）。

小批量梯度下降的主要优势在于它综合了随机梯度下降和批量梯度下降的优点。与随机梯度下降相比，小批量梯度下降的梯度估计更为稳定，因为它考虑了小批量内的多个样本；与批量梯度下降相比，小批量梯度下降具有更高的计算效率，因为它不需要处理整个数据集。

随机梯度下降收敛

在批量梯度下降中，我们可以令代价函数$J$为迭代次数的函数，绘制图表，根据图表来判断梯度下降是否收敛。但是，在大规模的训练集的情况下，这是不现实的，因为计算代价太大了。

在随机梯度下降中，我们在每一次更新 $$ 之前都计算一次代价，然后每$x$次迭代后，求出这$x$次对训练实例计算代价的平均值，然后绘制这些平均值与$x$次迭代的次数之间的函数图表。

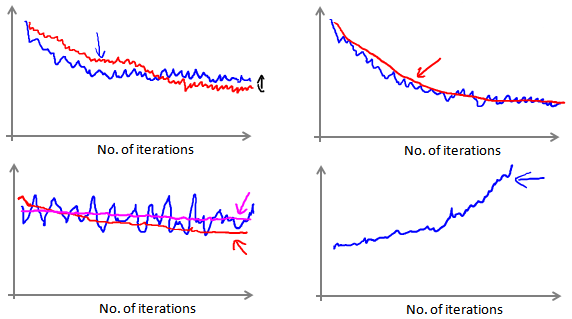
当我们绘制这样的图表时，可能会得到一个颠簸不平但是不会明显减少的函数图像（如上面左下图中蓝线所示）。我们可以增加$α$来使得函数更加平缓，也许便能看出下降的趋势了（如上面左下图中红线所示）；或者可能函数图表仍然是颠簸不平且不下降的（如洋红色线所示），那么我们的模型本身可能存在一些错误。

如果我们得到的曲线如上面右下方所示，不断地上升，那么我们可能会需要选择一个较小的学习率$α$。

我们也可以令学习率随着迭代次数的增加而减小，例如令：

$\alpha = \frac{const1}{iterationNumber + const2}$

随着我们不断地靠近全局最小值，通过减小学习率，我们迫使算法收敛而非在最小值附近徘徊。但是通常我们不需要这样做便能有非常好的效果了，对$α$进行调整所耗费的计算通常不值得

在线学习

在线学习（Online Learning）是一种机器学习的范式，其中模型能够逐步地从新的数据样本中进行学习，而不需要事先将整个训练数据集加载到内存中。与传统的批量学习（Batch Learning）不同，其中模型在整个数据集上进行训练，在线学习的模型能够根据即时接收到的数据动态地更新自身。

假设我们正在构建一个在线推荐系统，这个系统需要根据用户的历史行为和实时反馈来不断调整推荐的商品。

传统批量学习的方法：

在传统的批量学习中，我们可能会定期（比如每天或每周）使用整个历史数据集进行模型训练，然后将训练好的模型应用到实时推荐中。

在线学习的方法：

在在线学习中，我们可以采用增量学习的方式，即模型从每个新的用户行为中学到一些东西，并即时地更新推荐模型。例如，用户在网站上浏览商品、点击链接、购买商品等行为都可以作为新的数据进入模型。

只要网站在运行过程中，就可以利用随机梯度下降法从用户的点击中获取 $\left(x,y\right)$ 作为数据来训练$\theta$

$\theta:={\theta}_j-\alpha\left( h_{\theta}\left(x\right)-y \right){x_j}$

一旦对一个数据的学习完成了，我们便可以丢弃该数据，不需要再存储它了。这种方式的好处在于，我们的算法可以很好的适应用户的倾向性，算法可以针对用户的当前行为不断地更新模型以适应该用户

这样，推荐系统能够随着用户行为的变化动态地调整自己，而不必等到整个数据集重新训练。这种实时性和个性化是在线学习的优势之一，特别适用于需要快速适应变化和提供个性化服务的场景。

映射化简和数据并行

映射化简和数据并行对于大规模机器学习问题而言是非常重要的概念。之前提到，如果我们用批量梯度下降算法来求解大规模数据集的最优解，我们需要对整个训练集进行循环，计算偏导数和代价，再求和，计算代价非常大。如果我们能够将我们的数据集分配给不多台计算机，让每一台计算机处理数据集的一个子集，然后我们将计所的结果汇总在求和。这样的方法叫做映射简化

具体而言，如果任何学习算法能够表达为，对训练集的函数的求和，那么便能将这个任务分配给多台计算机（或者同一台计算机的不同CPU 核心），以达到加速处理的目的。

例如，我们有400个训练实例，我们可以将批量梯度下降的求和任务分配给4台计算机进行处理：

很多高级的线性代数函数库已经能够利用多核CPU的多个核心来并行地处理矩阵运算，这也是算法的向量化实现如此重要的缘故（比调用循环快）。