多元函数微积分学

多元函数

基本概念

定义

假设$D$是二维向量$(x,y)$的集合，$D$上的$\color{Salmon}{二元函数}$$\ f$是一个映射法则，它对$D$内的每一个有序对$(x,y)$指定唯一的一个实数：

$z=f(x,y),\quad (x,y)\in D$

如果用$P$来代替$(x,y)$的话，也可以写作：

$z=f(P),\quad P\in D$

$D$称为$f$的$\color{Salmon}{定义域}$，$x、y$（或$(x,y)$，或$P$）称为$f$的$\color{Salmon}{自变量}$，$z$称为$f$的$\color{Salmon}{因变量}$

定义域

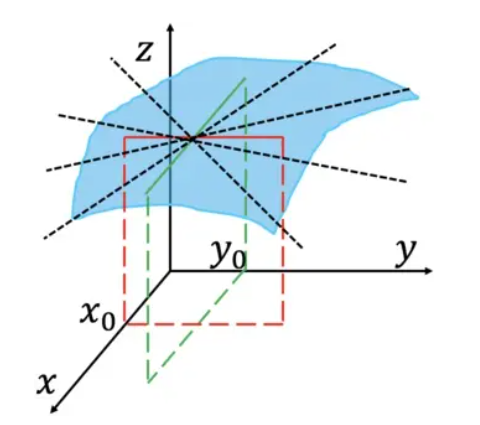
二元函数的定义域$D$是二维向量$(x,y)$的集合。因为二维向量$(x,y)$又代表了二维平面上的点，所以这样的集合也称为$\color{Salmon}{平面点集}$

邻域

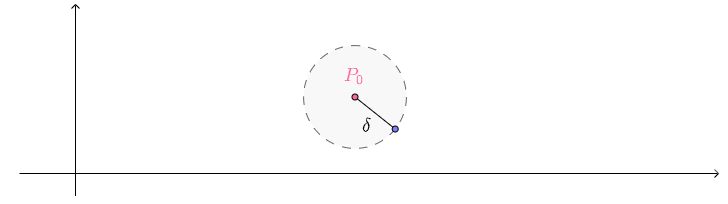
二维向量的邻域要比一维向量的复杂。对于二维向量$P_0(x_0,y_0)$而言，半径为$\delta\ \color{Salmon}{邻域}$可以表示为平面点集：

$U(P_0,\delta)=\{(x,y)\ |\ (x-x_0)^2 + (y-y_0)^2 < \delta^2\}$

该$\delta$邻域代表的是，以$P_0(x_0,y_0)$为圆心，半径为$\delta$的圆内的点（注意不包含的圆的边界）：

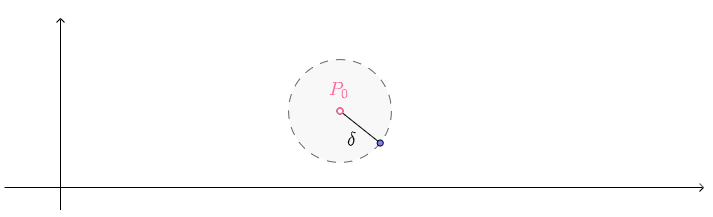
从$U(P_0,\delta)$中去掉中心$P_0(x_0,y_0)$，称为点$P_0(x_0,y_0)$的$\delta\ \color{Salmon}{去心邻域}$，记作：$\mathring{U}(P_0,\delta)$，可以图示为：

极限

聚点

如果对于任意给定的$\delta > 0$，点P的去心邻域$\mathring{U}(P,\delta)$内总有平面点集E中的点，那么称点$P$为$E$的$\color{Salmon}{聚点}$。

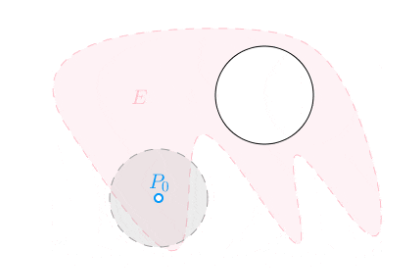
定义聚点是为了保证，从$P_0(x_0,y_0)$的某去心邻域内的某一点$P(x,y)$出发，至少能找到一串完全在$E$中的点来靠近$P_0$

极限定义：

设二元函数$f(x,y)$的定义域为$D，P_0(x_0,y_0)$是$D$的聚点。如果存在常数$L$，对于任意给定的正数$\epsilon$，总存在正数$\delta$，使得当点P(x,y)满足下列条件时：

$(x,y)\in D\cap \mathring{U}(P_0,\delta)$

都有：

$|f(x,y)-L| < \epsilon$

成立，那么就称常数$L$为函数$f(x,y)$当$(x,y)\to(x_0,y_0)$时的极限，记作：

$\lim_{(x,y)\to(x_0,y_0)}f(x,y)=L\quad 或\quad f(x,y)\to L\ \big(\ (x,y)\to(x_0,y_0)\ \big)$

因为这是二元函数的极限，所以也称作$\color{Salmon}{二重极限}$。

$\begin{array}{c|c} \hline \quad 一元函数的极限 \quad&\quad 二元函数的极限\quad\\ \hline \\ \quad 函数f(x)在\mathring{U}(x_0)上有定义\quad&\quad 二元函数f(x,y)的定义域为D \quad \\ \quad 0 < |x - x_0| < \delta \quad&\quad (x,y)\in D\cap \mathring{U}(P_0,\delta) \quad\\ \\ \hline \end{array}$

同一元函数的极限相同，随着$\epsilon$的缩小，始终能够找到合适的$\delta$，使得对应的函数值都在$\epsilon$规定的区间内

求重极限的方法：

利用极限性质(四则运算法则，夹逼原理)
消去分母中极限为0的因子
利用无穷小量与有界变量之积为无穷小量

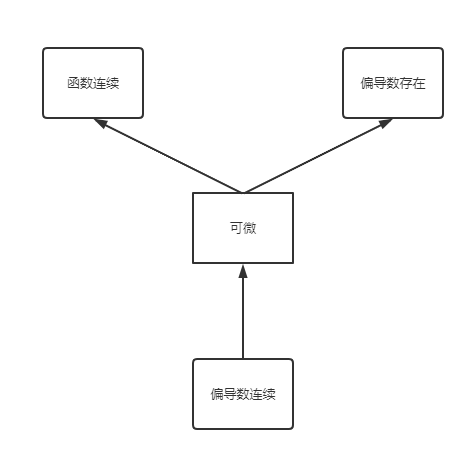
连续

二元函数$f(x,y)$的定义域为$D，P_0(x_0,y_0)$是$D$的聚点，且$P_0\in D$，如果：

$\lim_{(x,y)\to(x_0,y_0)}f(x,y)=f(x_0,y_0)$

那么称函数$f(x,y)$在点$P_0(x_0,y_0)\ \color{Salmon}{连续}$。

性质：

多元连续函数的和，差，积，商仍为连续函数
多元连续函数的复合函数也是连续函数
多元初等函数在其定义区域内连续
(最大值定理)：有界闭区间$D$上的连续函数在区域$D$上必能取得最大值和最小值
(介值定理)：有界闭区间$D$上的连续函数在区域$D$上必能取得介于最大值与最小值之间的任何值

全微分

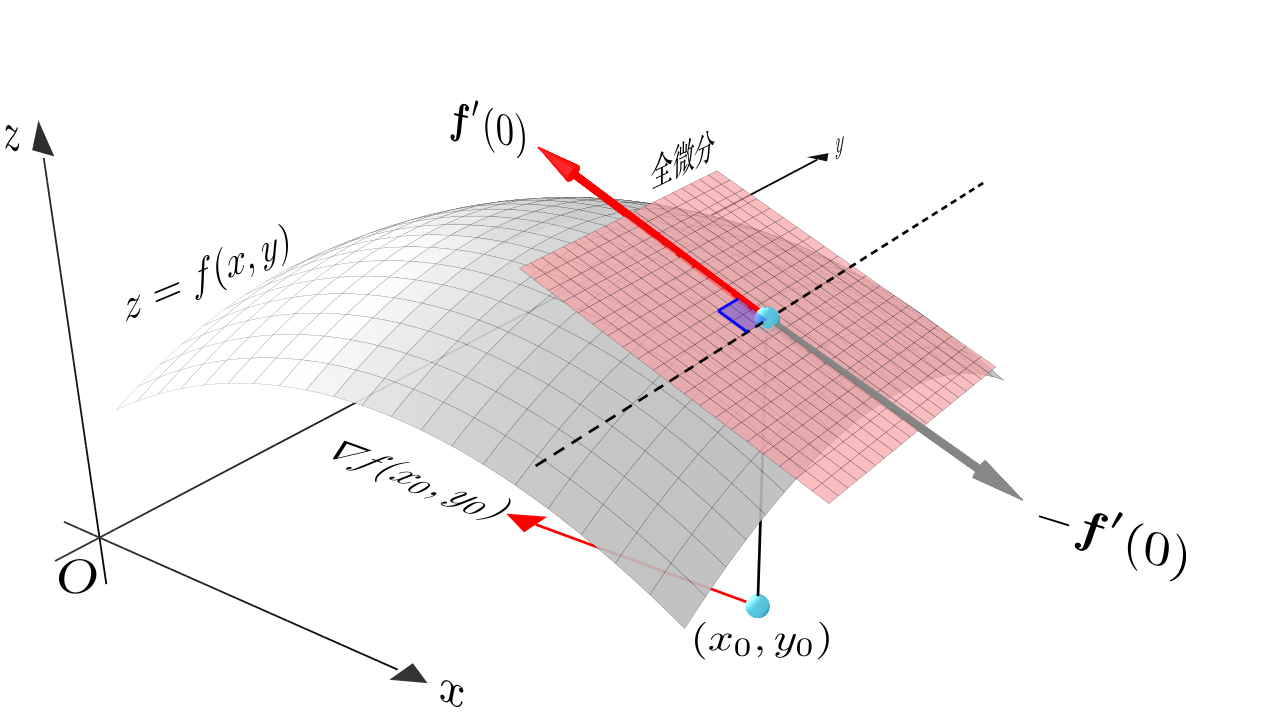
单变量微积分中，可以用$\color{Salmon}{切线}$来近似（“代替”）$x_0$点附近的曲线，在多变量函数中，需要找到一个平面来近似$(x_0,y_0)$附近的曲面

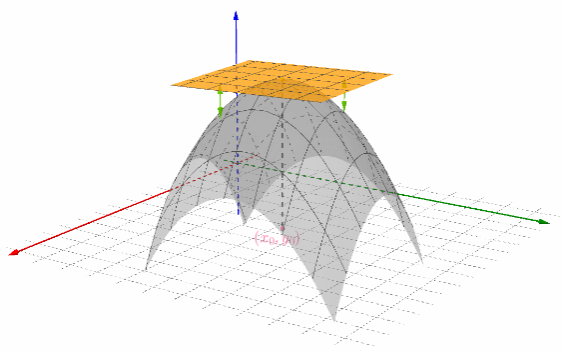
设函数$z=f(x,y)$在点$(x_0,y_0)$的某邻域内有定义，假设：

$\Delta x=x-x_0,\quad \Delta y=y-y_0$

如果函数$z=f(x,y)$在点$(x_0,y_0)$的$\color{Salmon}{全增量}$：

$\Delta z=f(x_0+\Delta x, y_0+\Delta y)-f(x_0, y_0)$

可以表示为：

$\Delta z=A\Delta x+B\Delta y+o(\rho)=A\Delta x+B\Delta y+\epsilon_1\Delta x+\epsilon_2\Delta y$

其中$A、B$不依赖于$\Delta x、\Delta y$，且：

$\rho=\sqrt{(\Delta x)^2+(\Delta y)^2},\quad \lim_{\Delta x\to 0}\epsilon_1=0,\quad \lim_{\Delta y\to 0}\epsilon_2=0$

那么称$z=f(x,y)$在点$(x_0,y_0)$处$\color{Salmon}{可微分}$，而$A\Delta x+B\Delta y$称为$z=f(x,y)$在点$(x_0,y_0)$处的$\color{Salmon}{全微分}$（或称为$\color{Salmon}{切平面}$），记作$\mathrm{d}z$，即：

$\mathrm{d}z=A\mathrm{d}x+B\mathrm{d}y$

核心是如下几点：

平面方程为（也就是所谓的全微分）：

$\mathrm{d}z=A\mathrm{d}x+B\mathrm{d}y$

曲面方程为（也就是所谓的全增量）：

$\Delta z=f(x_0+\Delta x, y_0+\Delta y)-f(x_0, y_0)$

曲面方程和平面方程的关系如下，可见两者相差了一个高阶无穷小，并且越接近$(x_0,y_0)$，两者越近似：

$\underbrace{\Delta z}_{\large 曲面方程}=\underbrace{A\Delta x+B\Delta y}_{\large 平面方程}+o(\rho)=A\Delta x+B\Delta y+\epsilon_1\Delta x+\epsilon_2\Delta y$ $o(\rho)=o(\sqrt{(\Delta x)^2+(\Delta y)^2})$

其中$\sqrt{(\Delta x)^2+(\Delta y)^2}$就是邻域内的点与$(x_0,y_0)$的距离。所以这个形式说明了，无论以什么方式靠近$(x_0,y_0)$，曲面和平面都会越来越接近（其差值趋于0）。

由于是平面，且是高阶无穷小，所以是$\color{Salmon}{最佳线性近似}$

偏导数

切平面

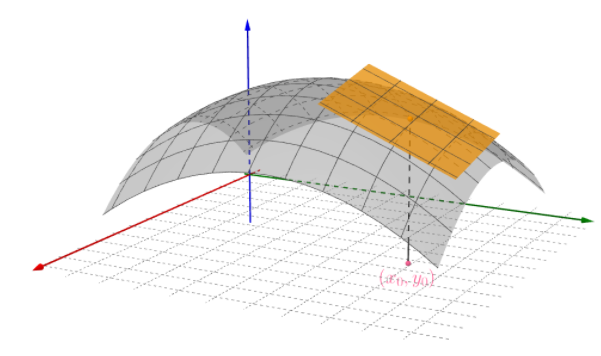
已知曲面在$(x_0,y_0)$点的切平面存在的前提，需要得到该切平面的方程

求解方法就是：需要知道其中两条不重合切线的方程就可以求出平面的方程。

$y=y_0$的交线

寻找最容易计算的两条切线。比如平面$y=y_0$和曲面$f(x,y)$相交的曲线如下：

这个曲线的方程为：

$\begin{cases} f(x,y)\\ y=y_0 \end{cases}$

也就说是，这个曲线的$y$自变量是固定的，是常数，因此曲线方程实际上相当于一元函数：

$\left. \begin{aligned} f(x,y)\\ y=y_0 \end{aligned} \right\} \implies f(x,y_0)$

该一元函数在$x=x_0$点（相当于二元函数在(x_0,y_0)点）的导数可以如下计算，知道该导数后就可以计算该曲线的切线了（这里暂时不计算切线，后面再来讨论）：

$f_x(x_0,y_0)=\left.\frac{\mathrm{d}}{\mathrm{d}x}f(x,y_0)\right|_{x=x_0}$

$x=x_0$的交线

同样的还有平面$x=x_0$和曲面$f(x,y)$相交的曲线如下：

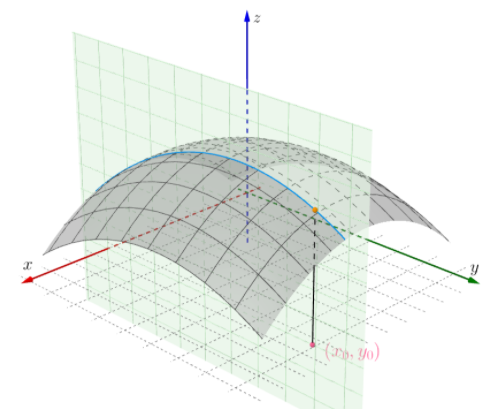
这条曲线的x自变量是固定的，是常数，因此曲线方程也是一元函数：

$\left. \begin{aligned} f(x,y)\\ x=x_0 \end{aligned} \right\} \implies f(x_0,y)$

该一元函数在$y=y_0$点（相当于二元函数在($x_0,y_0$)点）的导数可以如下计算，知道该导数也可以计算该曲线的切线了：

$f_y(x_0,y_0)=\left.\frac{\mathrm{d}}{\mathrm{d}y}f(x_0,y)\right|_{y=y_0}$

$x=x_0$与$y=y_0$是两个正交的平面：

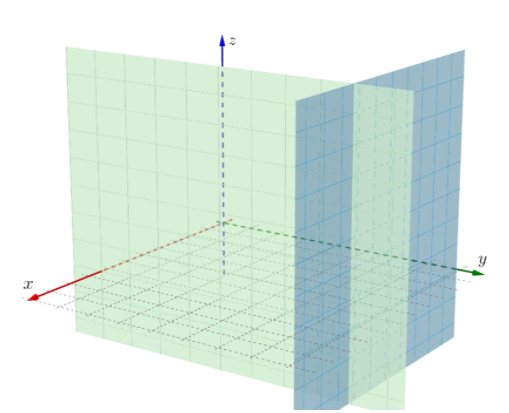
因此两条切线必然不重合，所以根据其两条交线求出其切平面

定义

在点$(x_0,y_0)，f(x,y)\ \color{Salmon}{关于x的偏导数}$是：

$\left.\frac{\partial f}{\partial x}\right|_{(x_0,y_0)}=\left.\frac{\mathrm{d}}{\mathrm{d}x}f(x,y_0)\right|_{x=x_0}=\lim_{h\to 0}\frac{f(x_0+h,y_0)-f(x_0,y_0)}{h}$

在点$(x_0,y_0)，f(x,y)\ \color{Salmon}{关于y的偏导数}$是：

$\left.\frac{\partial f}{\partial y}\right|_{(x_0,y_0)}=\left.\frac{\mathrm{d}}{\mathrm{d}y}f(x_0,y)\right|_{y=y_0}=\lim_{h\to 0}\frac{f(x_0,y_0+h)-f(x_0,y_0)}{h}$

只要该极限存在。

这两个偏导数就是刚才找到的两根切线的导数，通过它们就可以得到这两根切线的方程，进而可以得到切平面的方程

$\mathrm{d}z=f_x(x_0,y_0)\mathrm{d}x+f_y(x_0,y_0)\mathrm{d}y$

高阶偏导数

偏导数也是函数，所以可以继续对它求偏导数，所得结果可以称为$\color{Salmon}{二阶偏导数}$，根据求导次序不同有下列四种二阶偏导数：

$\begin{array}{l}{\frac{\partial}{\partial x}\left(\frac{\partial z}{\partial x}\right)=\frac{\partial^{2} z}{\partial x^{2}}=f_{x x}(x, y), \quad \frac{\partial}{\partial y}\left(\frac{\partial z}{\partial x}\right)=\frac{\partial^{2} z}{\partial x \partial y}=f_{x y}(x, y)} \\ {\frac{\partial}{\partial x}\left(\frac{\partial z}{\partial y}\right)=\frac{\partial^{2} z}{\partial y \partial x}=f_{y x}(x, y), \quad \frac{\partial}{\partial y}\left(\frac{\partial z}{\partial y}\right)=\frac{\partial^{2} z}{\partial y^{2}}=f_{yy}(x, y)}\end{array}$

上面的第二、三个又称为$\color{Salmon}{混合偏导数}$，它们满足下列条件时相等：

如果函数$z=f(x,y)$的两个混合偏导数在区域$D$内连续，那么必有：

$f_{x y}(x, y)=f_{y x}(x, y),\quad (x,y)\in D$

全微分与偏导数

如果函数$z=f(x,y)$在点$(x_0,y_0)$可微分，那么该函数在点$(x_0,y_0)$的偏导数$f_x(x_0,y_0)$、$f_y(x_0,y_0)$必定存在，且$z=f(x,y)$在点$(x_0,y_0)$的全微分为：

$\mathrm{d}z=f_x(x_0,y_0)\mathrm{d}x+f_y(x_0,y_0)\mathrm{d}y$

证明过程

根据函数$z=f(x,y)$在点$P(x_0,y_0)$可微分，可以得到对于$P$点的某个邻域内任意一点$P’(x_0+\Delta x,y+\Delta y)$有：

$\Delta z=A\Delta x+B\Delta y+o(\sqrt{(\Delta x)^2+(\Delta y)^2})$

当$\Delta y=0$时，上式也成立，可以改写为：

$\Delta z=A\Delta x+o(|\Delta x|)$

两边同时除以$\Delta x$。再令$\Delta x\to 0$，可得：

$f_x(x_0,y_0)=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}=A$

即偏导数$f_x(x_0,y_0)$存在，同理可得：

$f_y(x_0,y_0)=\lim_{\Delta y\to 0}\frac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{\Delta y}=B$

所以两个偏导数都存在，且这两个偏导就是我们想要找到的$A$和$B$，即：

$\mathrm{d}z=f_x(x_0,y_0)\mathrm{d}x+f_y(x_0,y_0)\mathrm{d}y$

可微分的条件

充分条件：导函数连续

已知函数$z=f(x,y)$的偏导数为$\frac{\partial f}{\partial x}$、$\frac{\partial f}{\partial y}$，那么：

$\frac{\partial f}{\partial x}、\frac{\partial f}{\partial y}\ 在\ (x_0,y_0)\ 连续\implies f(x,y)\ 在\ (x_0,y_0)\ 点可微分$

偏导数连续是指：

$\lim_{x\to x_0,y\to y_0}f_x(x,y)=f_x(x_0,y_0)\\ \lim_{x\to x_0,y\to y_0}f_y(x,y)=f_y(x_0,y_0)$

但是反过来是不行的

$\frac{\partial f}{\partial x}、\frac{\partial f}{\partial y}\ 在\ (x_0,y_0)\ 连续\mathrel{\rlap{\hskip .5em/}}\Longleftarrow f(x,y)\ 在\ (x_0,y_0)\ 点可微分$

即导函数连续可以推出可微分

充要条件：

$\lim_{(\Delta x,\Delta y)\to(0,0)}\frac{\Delta z-[f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y]}{\sqrt{((\Delta x)^2)+(\Delta y)^2}}$

该极限为$0$

显然，该极限的分母是邻域内的点与$(x_0,y_0)$的距离，而分子是$o(\rho)$，如果分子是高阶无穷小，则可以证明其可微性

常用的有界性技巧：

$\frac{\Delta x}{\sqrt{((\Delta x)^2)+(\Delta y)^2}}≤1\qquad 有界$

根据此定义，如果

$\lim_{(\Delta x,\Delta y)\to(0,0)}\frac{f(x,y)-f(0,0)-[f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y]}{g(x)}=c$

如果$g(x)$是$\sqrt{((\Delta x)^2)+(\Delta y)^2}$的高阶无穷小，那么就是可微的

可微与连续

已知函数$z=f(x,y)$，那么：

$f(x,y)\ 在\ (x_0,y_0)\ 点可微分\implies f(x,y)\ 在\ (x_0,y_0)\ 点连续$

可以这么理解，全微分意味着切平面存在，切平面是对切点周围曲面的线性近似；切平面是连续的，所以被近似的曲面也是连续的。

全导数

若$z=f(x,y)$是可微分的，而$x$和$y$是$t$的可导函数，则$z$是$t$的可导函数，并且：

$\frac{\mathrm{d}z}{\mathrm{d}t}=\frac{\partial z}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}t}+\frac{\partial z}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}t}$

这个导数可以看作过切点的曲线的导数，所以又被称为$\color{Salmon}{全导数}$。

通过多元函数的链式法则进行计算

xcv

全微分形式不变性

设函数$z=f(x,y)$具有连续偏导数，则有全微分：

$\mathrm{d}z=\frac{\partial z}{\partial x}\mathrm{d}x+\frac{\partial z}{\partial y}\mathrm{d}y$

不论$x、y$是中间变量还是自变量，全微分都保持上述形式，这称为$\color{Salmon}{全微分形式不变性}$

若$P(x,y)$和$Q(x,y)$有一阶连续偏导数，且$P(x,y)dx+Q(x,y)dy$是某一函数的全微分，则

$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$

因为$P(x,y)$本来就是对$x$求导的偏导数了，而$Q(x,y)$也本来就是对$y$求导的偏导数了

如果知道一个函数的全微分形式：$\mathrm{d}z=\frac{\partial z}{\partial x}\mathrm{d}x+\frac{\partial z}{\partial y}\mathrm{d}y$，根据此形式求其原函数一般有两种方法：

利用偏积分：$\frac{\partial z}{\partial x}\mathrm{d}x$的积分推出$z=f(x)+\phi(y)$的形式，$z_y=\frac{\partial z}{\partial y}$，求出$\phi’(y)$，然后积分，求出$\phi(y)$，最后就可以得到$z$的形式
直接凑微分

隐函数

假设$z=f(x,y)$在点$P_0(x_0,y_0)$的某一邻域内具有连续偏导数，且：

$f(x_0,y_0)=0,\quad f_y(x_0,y_0)\ne 0$

则方程$f(x,y)=0$在点$(x_0,y_0)$的某一邻域内恒能唯一确定一个连续且具有连续导数的函数$y=g(x)$，它满足条件$y_0=g(x_0)$，并有：

$\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{f_x}{f_y}$

该定理称为$\color{Salmon}{隐函数存在定理}$

证明过程也很简单：对方程$F(x,y)=0$求$x$的偏导数

$f_x’+f_y’·y'=0\implies y'=-\frac{f_x}{f_y}$

如果是由$f(x,y,z)=0$确定的隐函数$z=z(x,y)$，满足$f(x_0,y_0,z_0)=0$，$f_z’(x_0,y_0,z_0)≠0$,则有：

$\frac{\partial z}{\partial x}=-\frac{f_x}{f_z}\qquad\frac{\partial z}{\partial y}=-\frac{f_y}{f_z}$

求全微分的方法一般有3种

在$f(x,y,z)=0$的方程两端直接微分，然后代入具体的值
由隐函数求导公式直接求出$x$和$y$的偏导数
先将$x$单独代入到方程中，求$y$的偏导数，再反过来，最后得出全微分

证明$f(x,y)$可以表示为$g(ax+by)$，也就是证明$z=f(u,v)$这个多元函数与$v$无关

将$u=ax+by,v=y$，把$x$用$u$的方式带入进$f(u,v)$
证明$f_v=0$即可

梯度

一元函数的梯度

在解释梯度下降法之前，我们需要先从导数开始谈起

仅拥有一个自变量的函数称为一元函数，简记为 $y=f(x)$，我们一般通过导数的定义，求解$y$在$x_0$点处的变化率

定义如下：设函数$y=f(x)$在点$x_0$的某个邻域内有定义，当自变量$x$在$x_0$处取得增量$\Delta x$（点$x_0+\Delta x$仍在该邻域内）时，相应的，因变量取得增量$\Delta y=f(x_0+\Delta x)-f(x_0)$。如果$\Delta y$与$\Delta x$之比在$\Delta x\to 0$时的极限存在，那么称函数$y=f(x)$在点$x_0$处可导，并称这个极限为函数$y=f(x)$在点$x_0$处的导数，记为$f’(x_0)$，即：

$f'(x_0)=\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

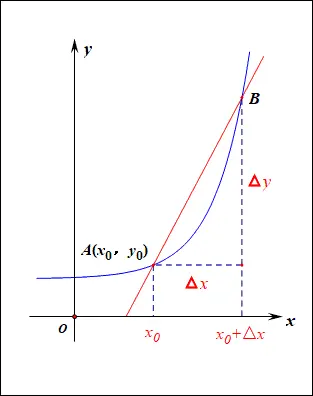
由于一元函数仅仅具有一个自变量 $x$ ，因此这类函数仅且只能反应函数沿 $x$ 轴方向的变化率

梯度是一个数学概念，是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大。

在一元函数中，函数的方向只有一维，把$f’(x_0)$称为函数在$x_0$点处的变化率，即是该点的梯度

多元函数的梯度

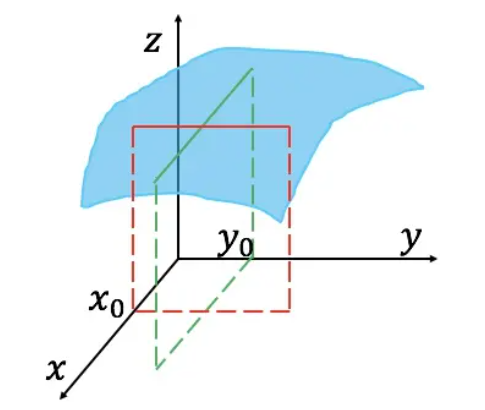
拥有多个自变量（≥2 ）的函数称为多元函数，以二元函数 $z=f(x,y)$ 为例讲解偏导数

由于二元函数具有两个自变量 $x,y$ ，因此函数图像为一个曲面。与一元函数类似，如何计算二元函数对曲面上一点 $(x_0,y_0)$ 的变化率呢？此处需要注意的是，因为过曲面上一点可以作出无数条切线，因此函数在该点也具有无数个变化率。为了简单起见，可以先考虑函数沿着两个坐标轴（ $x$ 轴， $y$ 轴）方向的变化率。

当自变量$y$固定在$y_0$，函数在点$x_0$处的变化率称为函数在点$(x_0,y_0)$处对$x$的偏导数，记作$f_x(x_0,y_0)$。
当自变量 $x$ 固定在 $x_0$ ，函数在点 $y_0$ 处的变化率称为函数在点 $(x_0,y_0)$ 处对 $y$ 的偏导数，记作 $f_y(x_0,y_0)$ 。

那么，知道了偏导数的基本概念，之后所要考虑的就是，求出函数在点 $(x_0,y_0)$ 处沿某一方向的变化率

假设某一方向的单位向量为 $e_l=(cos⁡α,sin⁡α)$ ， $α$ 为此向量与$x$轴正向夹角，显然根据 $α$ 的不同，此向量可以表示任意方向的单位向量。当点 $(x_0,y_0)$ 沿着该方向产生一个增量 $t$ 到达点 $(x_0+tcos⁡α,y_0+tsin⁡α)$ 时，函数 $z$ 也会产生一个增量 $Δz=f(x_0+tcos⁡α,y_0+tsin⁡α)−f(x_0,y_0)$ 。此时函数沿此方向的变化率为：

$\lim_{t \rightarrow 0^{+}} \frac{f(x_0+t \cos \alpha, y_0+t \sin \alpha)-f(x_0,y_0)}{t} \ = f_x(x_0,y_0) \cos \alpha + f_y(x_0,y_0) \sin \alpha$

（此处证明略过）

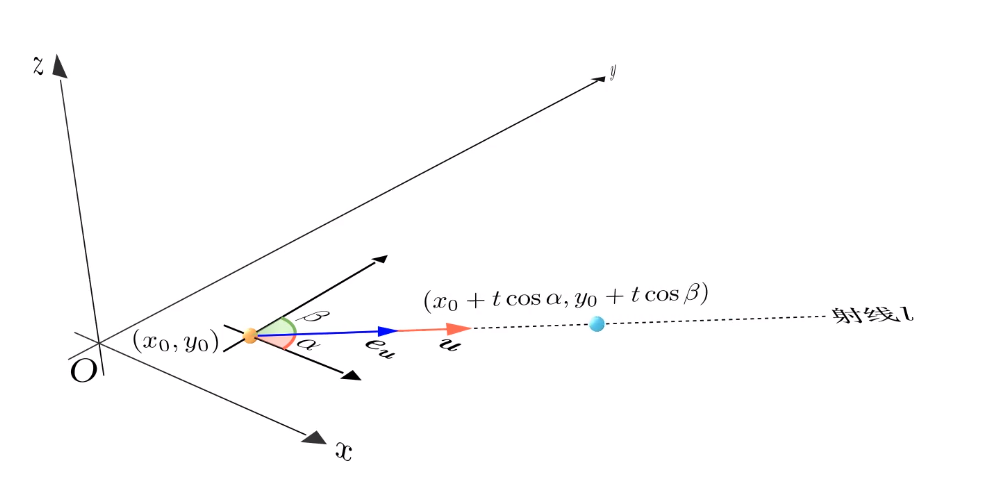
在了解了多元函数的方向导数之后，一个很自然的问题是：既然函数在点 $(x_0,y_0)$ 处沿着任意的方向都有一个变化率，那么沿着哪个方向（ α=? ）函数的变化率最大呢？

根据之前的介绍，函数 $z=f(x,y)$ 沿着任意方向（ α 取任意值）的变化率为： $f_x(x_0,y_0)cos⁡α+f_y(x_0,y_0)sin⁡α$ ，因此接下来只需求得使其达到最大值时的 α 便可解决上述问题

由于上式可以看成两个向量的内积(点积)

令：$\mathbf{g}=(f_x(x_0,y_0), f_y(x_0,y_0) ), \mathbf{e}_l=(\cos \alpha, \sin \alpha)$

则：$f_x(x_0,y_0) \cos \alpha + f_y(x_0,y_0) \sin \alpha = \mathbf{g} \cdot \mathbf{e}_l = |\mathbf{g}| |\mathbf{e}_l| \cos \theta = |\mathbf{g}| \cos \theta$

其中， $θ$ 为 $g$ 和 $e_l$ 的夹角。根据上式，可得出如下结论：

当 $θ=0$ 时，即 $e_l$ 和 $g$ 方向相同时，函数变化率最大，且在点 $(x_0,y_0)$ 处呈上升趋势；

最后，当点$(x_0,y_0)$确定后，向量$\mathbf{g}=(f_x(x_0,y_0), f_y(x_0,y_0) )$ 也随即确定,由于向量 $g$ 的方向为函数值增加最快的方向，而此方向经常被用于实际生活中，因此为便于表述，人们为其取了一个名字—梯度$\nabla f$

换而言之，多元函数在某一点的梯度是一个非常特殊的向量，其由多元函数对每个变量的偏导数组成（这即是为什么求梯度的时候需要对各个变量求偏导的原因），其方向为函数在该点增加最快的方向，大小为函数在该点的最大变化率。

极值

定理

设函数$z=f(x,y)$的定义域为$D，P_0(x_0,y_0)$是$D$的内点，则：
$f(x_0,y_0)$是$\color{Salmon}{极大值}$，当且仅当存在某个邻域$U(P_0)\subset D$，使得该邻域内所有异于$P_0$的点$(x,y)$，都有：

$f(x,y) < f(x_0,y_0)$

$f(x_0,y_0)$是$\color{Salmon}{极小值}$，当且仅当存在某个邻域$U(P_0)\subset D$，使得该邻域内所有异于$P_0$的点$(x,y)$，都有：

$f(x,y) > f(x_0,y_0)$

极大值和极小值都统称为$\color{Salmon}{极值}$，使得函数取得极值的点称为$\color{Salmon}{极值点}$。

条件

极值的必要条件：

设函数$z=f(x,y)$在点$(x_0,y_0)$处具有偏导数，且该点为极值点，则有：

$f_x(x_0,y_0)=f_y(x_0,y_0)=0$

极值的充分条件：

设函数$z=f(x,y)$在点$(x_0,y_0)$的某邻域内连续且有一阶及二阶连续偏导数，则其二阶导数，即海森矩阵为：

$H=\frac{\partial^2 z}{\partial(x,y)^2}=\begin{pmatrix}f_{xx}&f_{xy}\\f_{yx}&f_{yy}\end{pmatrix}$

如果又有：

$f_x(x_0,y_0)=f_y(x_0,y_0)=0$

那么：

$f(x_0,y_0)$为极大值，当$f_{xx} < 0$且$|H| > 0$；
$f(x_0,y_0)$为极小值，当$f_{xx} > 0$且$|H| > 0$；
$f(x_0,y_0)$非极值点，当$|H| < 0$；
$f(x_0,y_0)$无法判断是否为极值点，当$|H| = 0$。

拉格朗日乘数法

拉格朗日乘数法用于求解在约束条件下的极值

要求约束下的最值问题：

$\begin{gather} \min\max\ z=f(x,y)\\ s.t.\ g(x,y)=0 \end{gather}$

在极值点可以列出如下方程组：

$\begin{cases} \nabla f=\lambda\nabla g\\ \\ g(x,y)=0 \end{cases}$

其中$\nabla f$是函数的梯度

$\nabla f=\begin{pmatrix}f_x\\f_y\end{pmatrix}$

$\nabla g$是约束条件的梯度向量

$\nabla g=\begin{pmatrix}g_x\\g_y\end{pmatrix}$

$\nabla f=\lambda\nabla g$成立说明梯度向量平行

解该方程组可以求出极值点，这就是$\color{Salmon}{拉格朗日乘数法}$。

下面是三元函数，在两个约束下的最值问题：

$\begin{aligned} \min\max\ w=f(x,y,z)\\ s.t.\ \begin{cases} g_1(x,y,z)=0\\ g_2(x,y,z)=0 \end{cases} \end{aligned}$

解法是：

$\begin{cases} \nabla f=\lambda\nabla g_1+\mu\nabla g_2\\ \\ g_1(x,y,z)=0\\ \\ g_2(x,y,z)=0\\ \end{cases}$

拉格朗日乘数法可以用行列式来简化运算，方程有非零解的前提是行列式的值等于0

求连续函数$f(x,y)$在有界闭区域$D$上的最大最小值

求$f(x,y)$在$D$内部可能的极值点(导数=0的点)
求$f(x,y)$在$D$的边界上的最大最小值(拉格朗日乘数法找符合条件的点)
比较

二重积分

概念

设$f(x,y)$是有界闭区域$D$上的有界函数，将闭区域$D$任意分成$n$个小闭区域：

$\Delta A_1,\Delta A_2,\cdots,\Delta A_i,\cdots,\Delta A_n$

其中$\Delta A_i$表示第$i$个小闭区域，也表示它的面积，规定$\Delta A_i$中最长的直径（一个闭区域的直径是指区域上任意两点间距离的最大者）为$\lambda$，在每个$\Delta A_i$内任取一点$(x_i,y_i)$，可以得到级数：

$\sum_{i=0}^{n}f(x_i,y_i)\Delta A_i$

如果当$\lambda\to 0$时，无论如何划分闭区域$D$，无论怎样选取$(x_i,y_i)$，该级数的极限总是存在，那么称此极限为函数$f(x,y)$在闭区域$D$上的$\color{Salmon}{二重积分}$，记作：

$\iint_\limits{D}f(x,y)\mathrm{d}A=\lim_{\lambda\to 0}\sum_{i=0}^{n}f(x_i,y_i)\Delta A_i$

其中$f(x,y)$称为$\color{Salmon}{被积函数}$，$\mathrm{d}A$称为$\color{Salmon}{面积微分}$，$x$与$y$称为$\color{Salmon}{积分变量}$，$D$称为$\color{Salmon}{积分区域}$。

实际上就是说区域$D$上的函数$z=f(x,y)$：

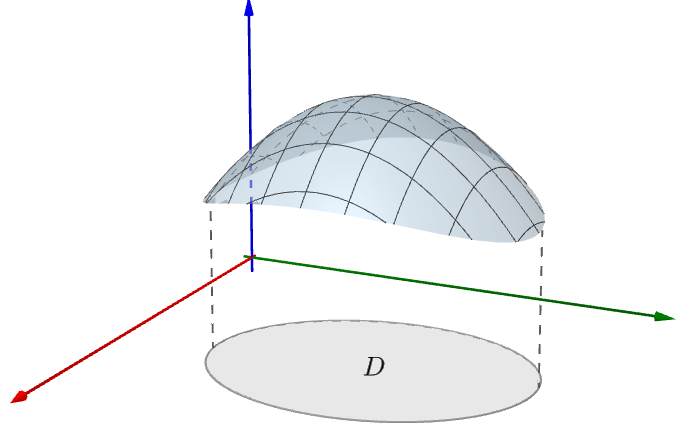
该曲面下的体积，可以通过任意的，无穷划分D后得到的柱体来计算

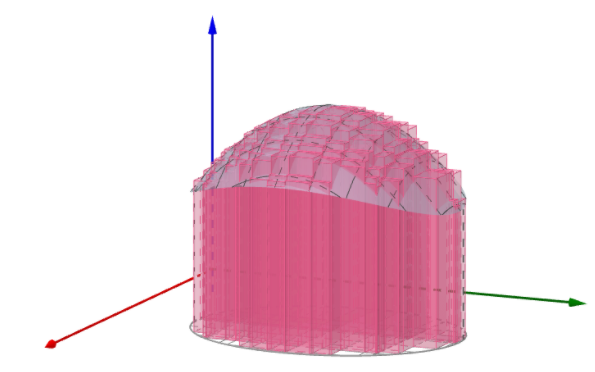
对区域$D$进行矩形划分时，边长可记作$\Delta x_i、\Delta y_i$

也就是说有：

$\Delta A_i=\Delta x_i\Delta y_i$

所以$D$区域上的曲面$z=f(x,y)$下的体积可以表示为：

$\iint_\limits{D}f(x,y)\mathrm{d}A=\lim_{\lambda\to 0}\sum_{i=0}^{n}f(x_i,y_i)\Delta x_i\Delta y_i$

因此二重积分有另外一种等价的表示形式：

$\iint_\limits{D}f(x,y)\mathrm{d}A=\iint_\limits{D}f(x,y)\mathrm{d}x\mathrm{d}y$

因为在直角坐标系中，才进行矩形划分，所以$\mathrm{d}x\mathrm{d}y$也被称为$\color{Salmon}{直角坐标系中的面积微分}$

性质

设$f(x,y)$，$g(x,y)$都是有界闭区域D上的有界函数，$\alpha、\beta$为常数，则：

齐次性：

$\iint_\limits{D}\alpha f(x,y)\mathrm{d}A=\alpha\iint_\limits{D}f(x,y)\mathrm{d}A$

可加性：

$\iint_\limits{D}\Big(f(x,y)+g(x,y)\Big)\mathrm{d}A=\iint_\limits{D}f(x,y)\mathrm{d}A+\iint_\limits{D}g(x,y)\mathrm{d}A$

区域可加性：

$\iint_\limits{D}f(x,y)\mathrm{d}A=\iint_\limits{D_1}f(x,y)\mathrm{d}A+\iint_\limits{D_2}f(x,y)\mathrm{d}A$

不等式：
$f(x,y) \le g(x,y)\implies\iint_\limits{D}f(x,y)\mathrm{d}A \le \iint_\limits{D}g(x,y)\mathrm{d}A$
假设$f(x,y)$在区域$D$中，下界为$m$，上界为$M$，即：
$m\le f(x,y)\le M$
如果区域$D$的面积为$A$，那么根据上述定理可以得出：
$mA\le \iint_\limits{D}f(x,y)\mathrm{d}A \le MA$
中值定理

设函数$f(x,y)$在闭区域$D$上连续，$A$是区域$D$的面积，则在$D$上至少存在一点$(\xi,\mu)$，使得：
$\iint_\limits{D}f(x,y)\mathrm{d}A=f(\xi,\mu)A$
中值定理本质是：定义在区域$D$上的函数$z=f(x,y)$，必然可以找到某点$(\xi,\mu)$，以该点的函数$f(\xi,\mu)$做一个平面，使得曲面下的体积和平面下的体积相等：

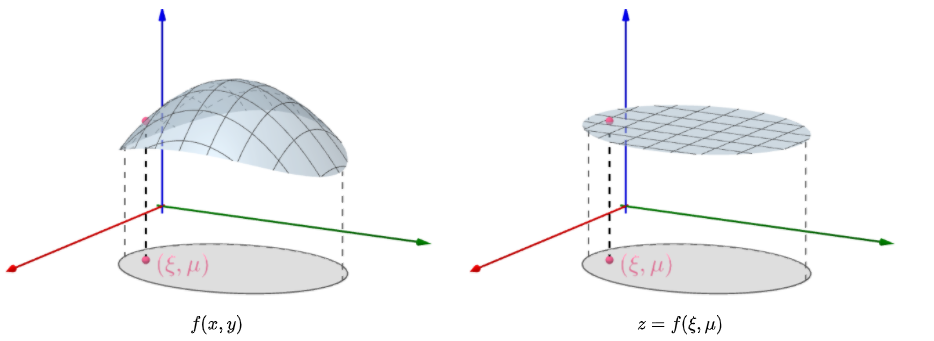
计算

常规坐标

$X$型区域：

比如区域$D$：

$D=\{(x,y)|a \le x \le b, g_1(x) \le y \le g_2(x)\}$

区域$D$的特征是$x$在区间$[a,b]$上变化，而$y$的范围依赖于$x$的函数，这样的区域称为$\color{Salmon}{X型区域}$）。下面就是三种$X$型区域：

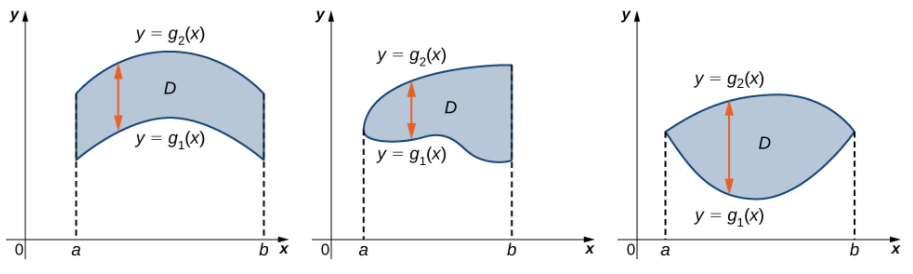
截面面积为

$A(x_0)=\int_{g_1(x_0)}^{g_2(x_0)}f(x_0, y)\mathrm{d}y$

体积为：

$V=\int_{a}^{b}A(x)\mathrm{d}x$

二重积分为：

$V=\iint_\limits{D}f(x,y)\mathrm{d}A=\int_{a}^{b}\int_{g_1(x)}^{g_2(x)}f(x, y)\mathrm{d}y\mathrm{d}x$

$Y$型区域

比如区域$D$：

$D=\{(x,y)|c \le y \le d, h_1(y) \le x \le h_2(y)\}$

区域$D$的特征是$y$在区间$[c,d]$上变化，而$x$的范围依赖于$y$的函数，这样的区域称为$\color{Salmon}{Y型区域}$。比如下面就是两种$Y$型区域：

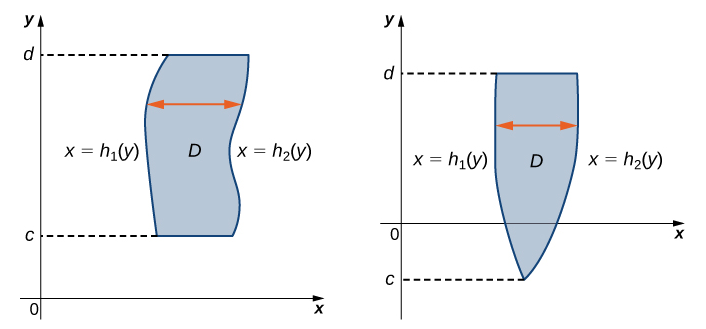
$Y$型区域上的体积为：

$V=\iint_\limits{D}f(x,y)\mathrm{d}A=\int_{c}^{d}\int_{h_1(y)}^{h_2(y)}f(x, y)\mathrm{d}x\mathrm{d}y$

总结：

若$f(x,y)$在区域$D$上连续：

若区域$D$为$a \le x \le b, g_1(x) \le y \le g_2(x)$，其中$g_1、g_2$在$[a,b]$上连续，则：
$\iint_\limits{D}f(x,y)\mathrm{d}A=\int_{a}^{b}\Big[\int_{g_1(x)}^{g_2(x)}f(x, y)\mathrm{d}y\Big]\mathrm{d}x$
若区域$D$为$c \le y \le d, h_1(y) \le x \le h_2(y)$，其中$h_1、h_2$在$[c,d]$上连续，则：
$\iint_\limits{D}f(x,y)\mathrm{d}A=\int_{c}^{d}\Big[\int_{h_1(y)}^{h_2(y)}f(x, y)\mathrm{d}x\Big]\mathrm{d}y$

当遇到不好积分的区域时，可以先画出积分区域，然后交换积分的次序，从而达到简化积分的效果

极坐标

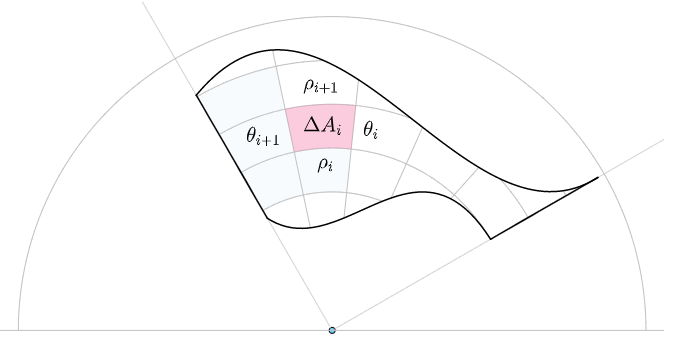
$\Delta A_i$在极坐标系下可以表示为：

$\Delta A_i=\{(\rho,\theta)|\rho_i\le\rho\le\rho_{i+1},\theta_i\le\theta\le\theta_{i+1}\}$

可见该区域的$\rho、\theta$都在两个常数之间，所以称为$\color{Salmon}{极坐标矩形}$

$\Delta A_i$的面积可以看作两个大小扇形的面积差，其中$\Delta \theta_i=\theta_{i+1}-\theta_{i}$：

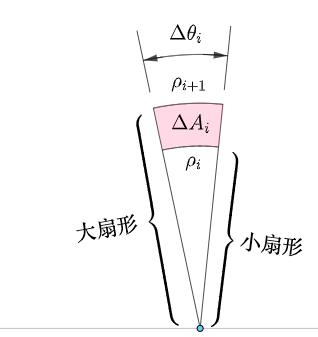
两个扇形的面积分别为：

$大扇形=\frac{1}{2}\rho_{i+1}^2\Delta \theta_i,\quad 小扇形=\frac{1}{2}\rho_{i}^2\Delta \theta_i$

所以：

$\begin{aligned} \Delta A_i &=大扇形-小扇形\\ \\ &=\frac{1}{2}\rho_{i+1}^2\Delta \theta_i-\frac{1}{2}\rho_{i}^2\Delta \theta_i\\ \\ &=\frac{\rho_{i+1}+\rho_{i}}{2}\cdot(\rho_{i+1}-\rho_{i})\cdot(\theta_{i+1}-\theta_{i})\\ \\ &=\overline{\rho_i}\cdot\Delta \rho_i\cdot\Delta\theta_i \end{aligned}$

而在极坐标下的二重积分可以这样表示：

该曲面下的体积可以用这些柱体的和来逼近：

$V\approx \sum_{i=1}^{n}f(\rho_i,\theta_i)\Delta A_i=\sum_{i=1}^{n}f(\rho_i,\theta_i)\overline{\rho_i}\cdot\Delta \rho_i\cdot\Delta\theta_i$

假设$\lambda=\max(\Delta A_i)$，当$\lambda\to 0$时，就可以得到曲面下的体积：

$V=\lim_{\lambda\to 0}\sum_{i=1}^{n}f(\rho_i,\theta_i)\Delta A_i=\lim_{\lambda\to 0}\sum_{i=1}^{n}f(\rho_i,\theta_i)\overline{\rho_i}\cdot\Delta \rho_i\cdot\Delta\theta_i$

写作二重积分的形式就是：

$V=\iint_\limits{D}f(\rho,\theta)\mathrm{d}A=\iint_\limits{D}f(\rho,\theta)\rho\mathrm{d}\rho\mathrm{d}\theta$

其中，$\rho\mathrm{d}\rho\mathrm{d}\theta$称为$\color{Salmon}{极坐标系下的面积微分}$

计算：

若区域$D$为$\alpha \le \theta \le \beta, h_1(\theta) \le \rho \le h_2(\theta)$，其中$h_1、h_2$在$[\alpha,\beta]$上连续，则：

$\iint_\limits{D}f(x,y)\mathrm{d}A=\int_{\alpha}^{\beta}\Big[\int_{h_1(\theta)}^{h_2(\theta)}f(\rho, \theta)\rho\mathrm{d}\rho\Big]\mathrm{d}\theta$

次序的先后取决于从零点引射线，先经过的曲线在前，后经过的在后

常规坐标与极坐标

$\iint_\limits{D}f(x,y)\ \color{OrangeRed}{\mathrm{d}x\mathrm{d}y}\ =\iint_\limits{D}f(\rho,\theta)\ \color{ForestGreen}{\rho\mathrm{d}\rho\mathrm{d}\theta}$ $x\implies \rho cos\theta\qquad y\implies\rho sin\theta\qquad dxdy=\rho\mathrm{d}\rho\mathrm{d}\theta$

可以利用极坐标来解某些周期性积分

比如

$\iint_\limits{D}|ax+by|dxdy\qquad (D(x,y)|x^2+y^2≤1)$

可以化为如下形式：

$\int^{2\pi}_0d\theta \int^1_0|3rcos\theta+4rsin\theta|rdr$

先把$r$算出来，然后利用辅助角公式变为如下形式：

$\frac{1}{3}×5×\int^{2\pi}_0|\frac{3}{5}cos\theta+\frac{4}{5}sin\theta|d\theta=\frac{5}{3}\int^{2\pi}_{0}|sin(\theta+\theta_0)|d\theta$

将$\theta+\theta_0=t$带入，变为：

$\frac{5}{3}\int^{\theta_0+2\pi}_{\theta_0}|sint|dt=\frac{20}{3}$

面对极坐标方程时，还原成常规坐标方程时：

比如$r=1-cos\theta$

$\begin{align} x=rcos\theta\\ y=rsin\theta\\ \frac{dy}{dx}=\frac{dy}{d\theta}·\frac{d\theta}{dx} \end{align}$

对称性

积分域$D$关于$y$轴对称，如果$f(x,y)$是$x$的偶函数： $\iint_\limits{D}f(x,y)dA=2\iint_\limits{D_{x>0}}f(x,y)dA$ 如果$f(x,y)$是$x$的奇函数，那么积分值为$0$

积分域$D$关于$x$轴对称，如果$f(x,y)$是$y$的偶函数： $\iint_\limits{D}f(x,y)dA=2\iint_\limits{D_{y>0}}f(x,y)dA$ 如果$f(x,y)$是$y$的奇函数，那么积分值为$0$

积分域$D$关于$y=x$轴对称，则： $\iint_\limits{D}f(x,y)dA=\iint_\limits{D}f(y,x)dA$ 此条性质常被用于如下变化： $\iint_\limits{D}x^2dA=\frac{1}{2}\iint_\limits{D}x^2+y^2dA$

在利用区域对称性解题时，注意添加曲线让区域保持对称

形心

$x_0=\frac{\int_a^b xf(x)dx}{\int_a^b f(x)dx}\qquad y_0=\frac{\frac{1}{2}\int_a^b f(x)^2dx}{\int_a^b f(x)dx}$

推导过程

$x_0=\frac{\iint_D xdxdy}{\iint_D dxdy}=\frac{\int_a^bxdx\int_0^{f(x)}dy}{\int_a^bdx\int^{f(x)}_0dy}=\frac{\int_a^b xf(x)dx}{\int_a^b f(x)dx}$ $y_0=\frac{\iint_D ydxdy}{\iint_D dxdy}=\frac{\int_a^bdx\int_0^{f(x)}ydy}{\int_a^bdx\int^{f(x)}_0dy}=\frac{\frac{1}{2}\int_a^b f(x)^2dx}{\int_a^b f(x)dx}$

常见图形

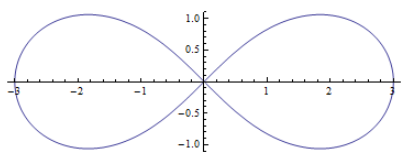
双纽线

$(x^2+y^2)^2=a^2(x^2-y^2)$

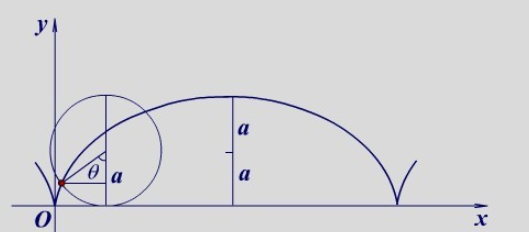
摆线

$x=a(t-sint)$

$y=a(1-cost)$

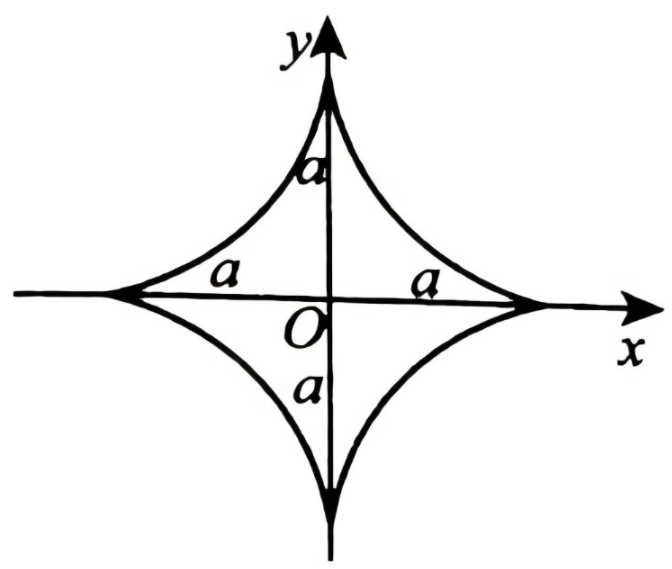
星形线

$x=acos^3t$

$y=asin^3t$

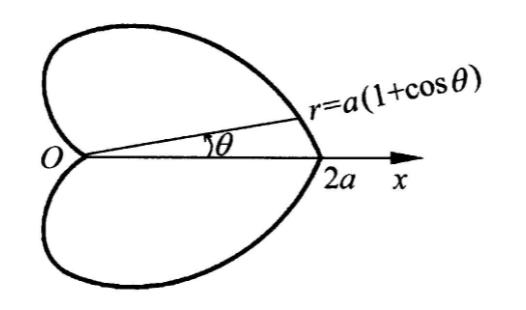
心形线

$\rho=a(1+cos\theta)$