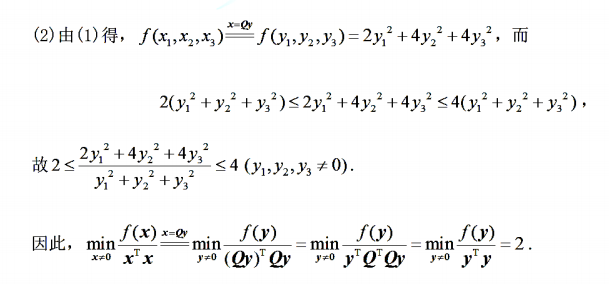数学真题
函数,极限,连续
选
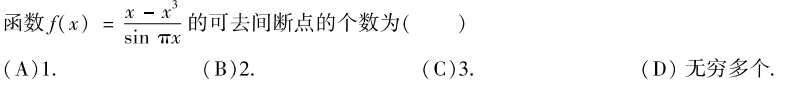
解析:
分母:$sin\pi x$在$x$为整数时$\to 0$,
分子在$x=0,x=1,x=-1$时也为0,
依次将0,-1,1代入求极限,可以得到,这三点都是可去间断点,所以选C
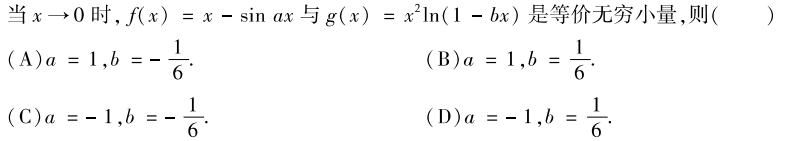
解析:
- 直接用$x-sinx \sim \frac{1}{6}x^3$这个结论
- 洛必达法则
所以选A

解析:可能点有三个:$1,-1,0,x=1$时,可以直接约去,$x=0$时,极限为1,故只有$x=-1$一个点,选B
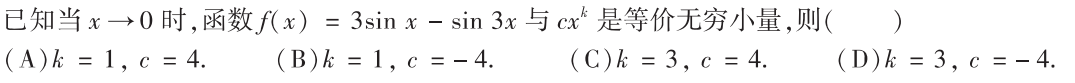
解析:用$x-sinx \sim \frac{1}{6}x^3$代换,选C
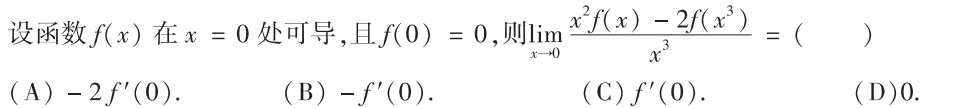
解析:将极限拆开,考察的是导数的定义,选B

解析:首先有水平渐近线,故无斜渐近线,还有1条垂直渐近线,故有2条
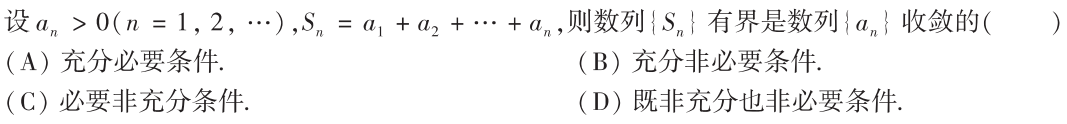
解析:$S_{n+1}-S_{n}=a_{n+1}$,所以如果$S_n$有界,那么$a_n$肯定会收敛到0,而$a_n$收敛,假设$a_n=\frac{1}{n}$,那么$S_n$不收敛,所以是充分非必要条件,选B
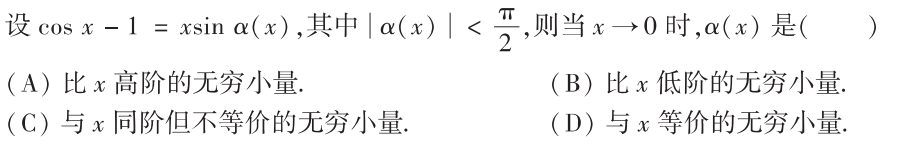
解析:等价代换之后,很明显选C

解析:等价代换后即可,B
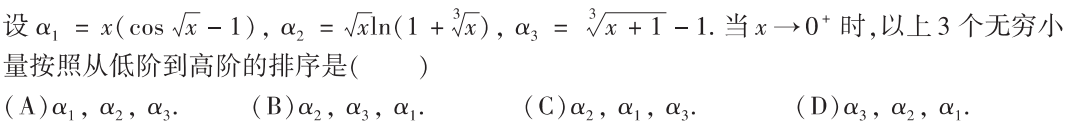
解析:简单代换后,分别是 $2 ,\frac{5}{6},1$,所以选B
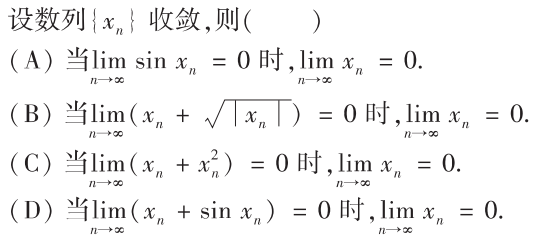
解析:只有D满足,不会有正负抵消的情况

解析:$e^{x}$泰勒展开即可


解析:显然是3,选C

解析:算出结果来,选D
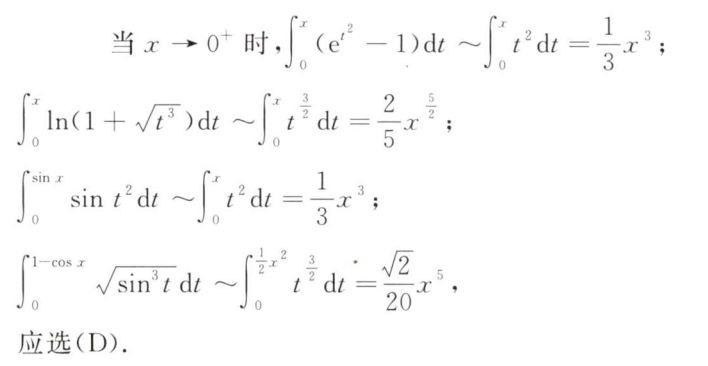

解析:2(3+1)=8,所以是高阶无穷小,选C

解析:$secx$是偶函数,所以$a=0$,而$secx$在零点附近是大于1的,所以$b>0$,选D

解析:首先1,4是对的,重点关注3,其中$o(a(x))$表示的是$a(x)$的高阶无穷小,当然成立,所以选C
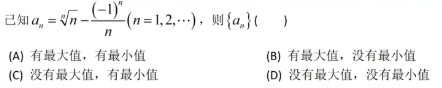
解析:本质上是看$a_n$的上限与下限,$a_1>1$而$a_2<1$,又$n\to \infty$ 时 $a_n=1$,所以$a_1>a_n>a_2$,有最大值,也有最小值

解析:AB都错,因为$cosx_n$是偶函数,C也错,$x_n$一定存在,D正确
填
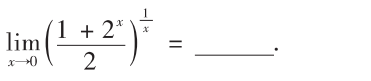
解析:用$1^{\infty}$的常见做法即可
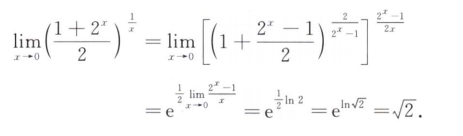
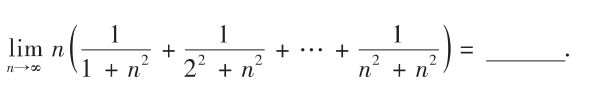
解析:用定积分定义: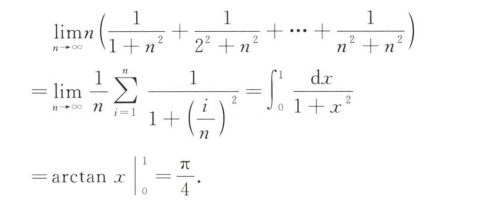
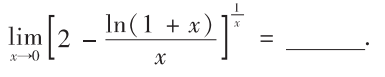
解析:用$1^{\infty}$的方法即可
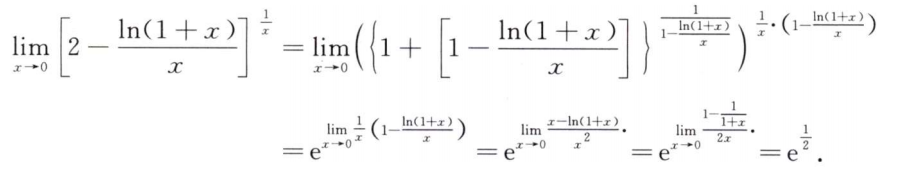
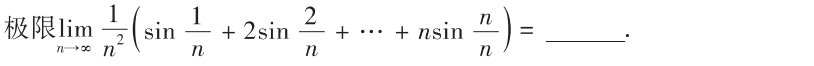
解析:定积分的定义
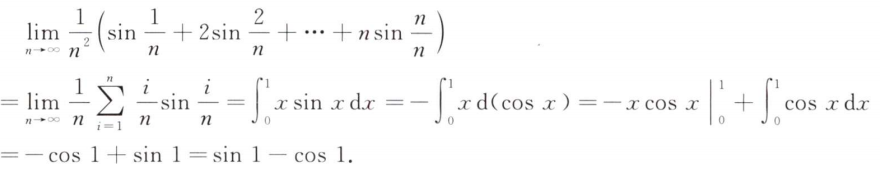
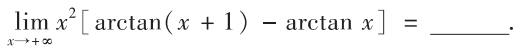
解析:直接用$arctanx$的运算公式简化运算,或者是拉格朗日定理

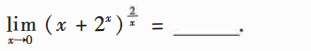
解析:用$1^{\infty}$的结论
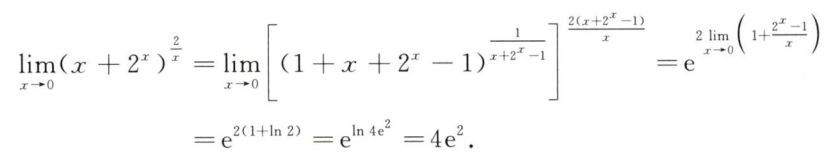
解析:把$x$次幂提出来更好算

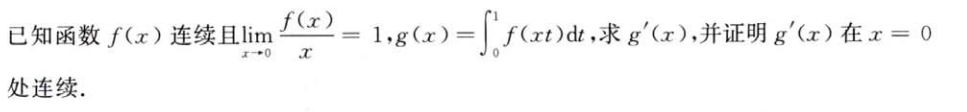
解析:证明$g’(x)$连续,那么要证明在不可导点的导数和常规的导数一致
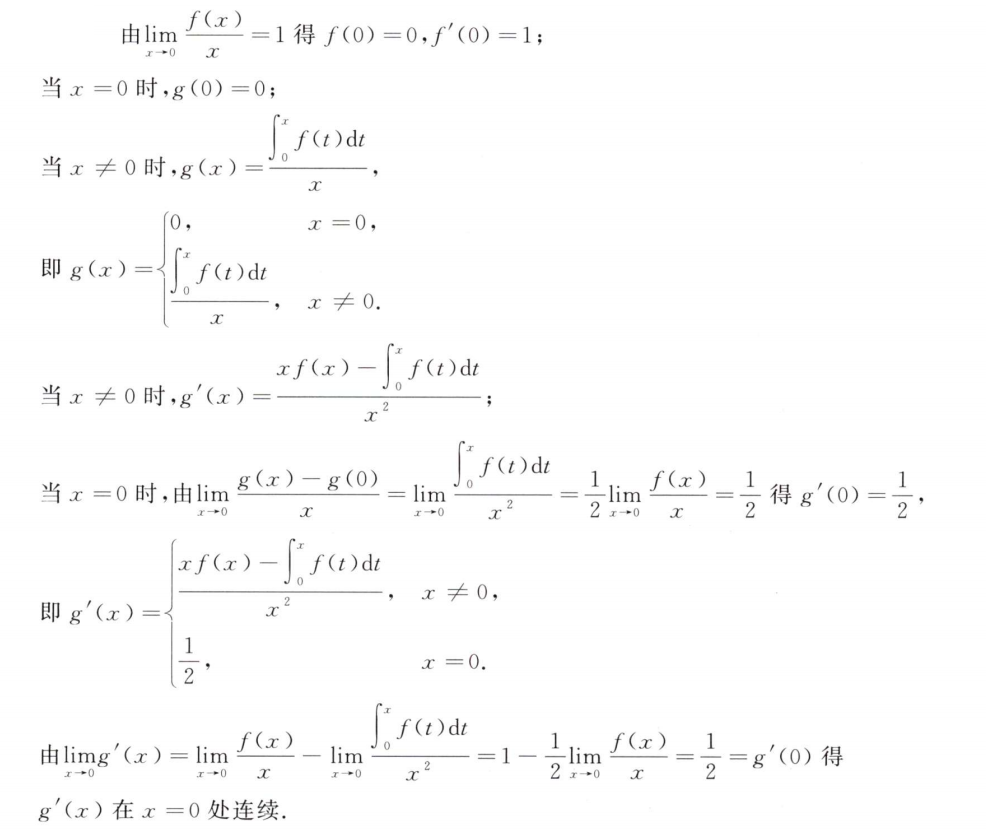

解析:$1^{\infty}$方法
综
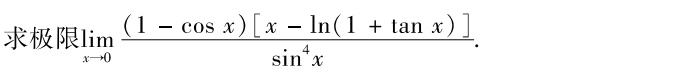
解析:本题难度较低,分母可以直接化成$x^4$,然后$1-cos\sim\frac{1}{2}x^2,x-ln(1+x)\sim\frac{1}{2}x^2$,可以很轻松的求出是$\frac{1}{4}$
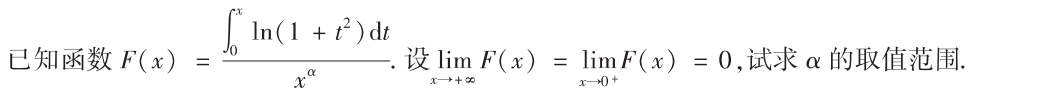
解析:分别求极限即可
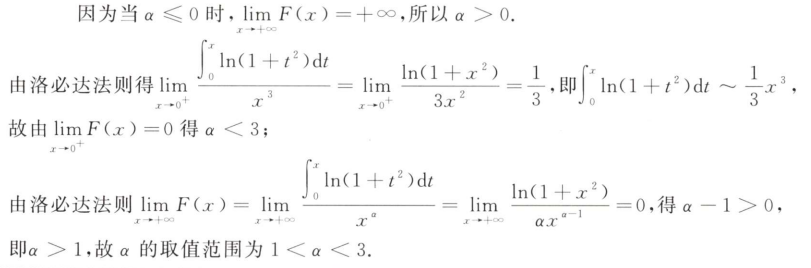
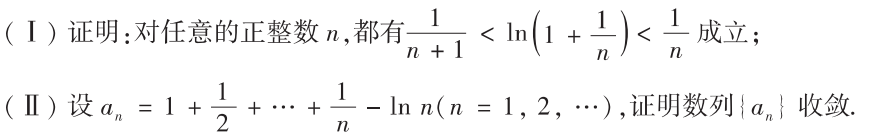
解析:第一问好证明,第二问需要观察到$x>ln(1+x)$,将所有$x$替换成$ln(1+x)$证明其有下界
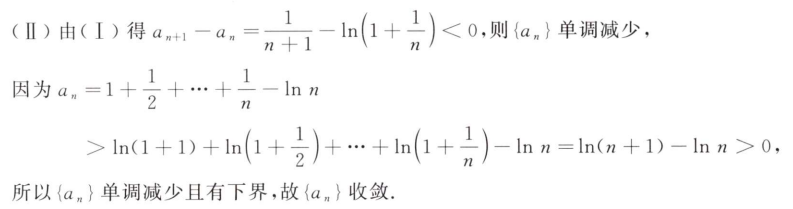

解析:重复用洛必达法则即可求解:
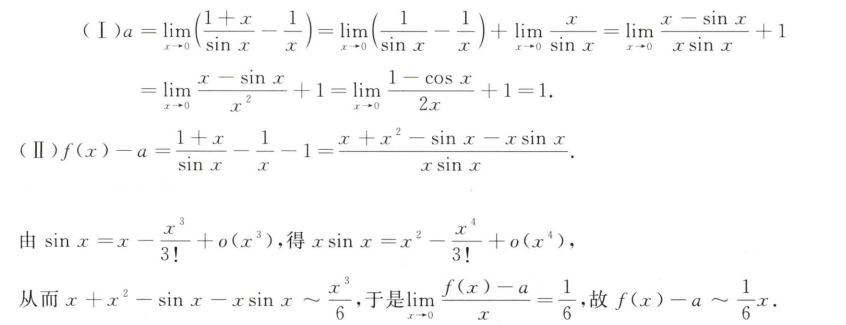

第一问可用求和公式+单调性解决,而第二问需要用到单调有界法则证明极限存在
第二问解法将$x_{n}$带入到了$f_NaN$的序列中去,从而判断出$x_n>x_{n+1}$


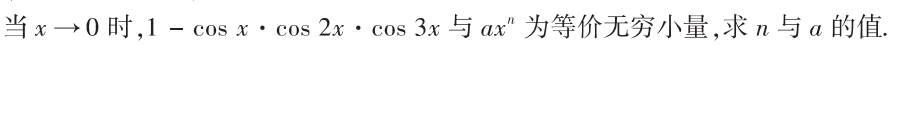
解析:这种题直接泰勒展开
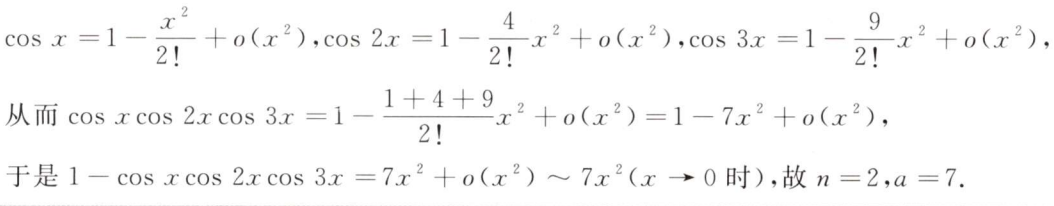
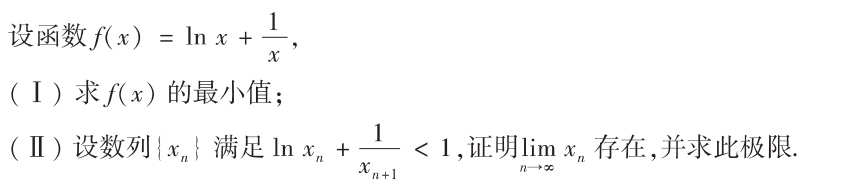
解析:第1问只要算导数即可,第2问最难的是找到$x_n$的上界

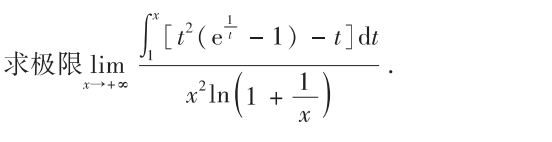
解析:到等价无穷小的代换以及洛必达法则
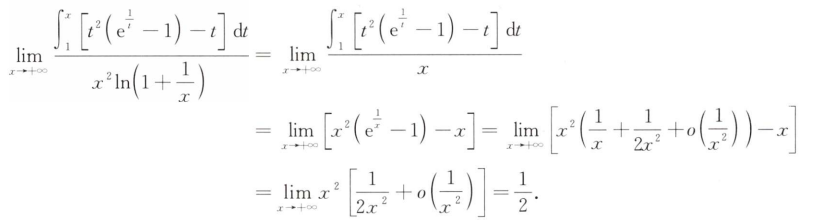

解析:先求出$f_{n}(x)$的表达式,然后算出$S_n$的表达式,然后求极限

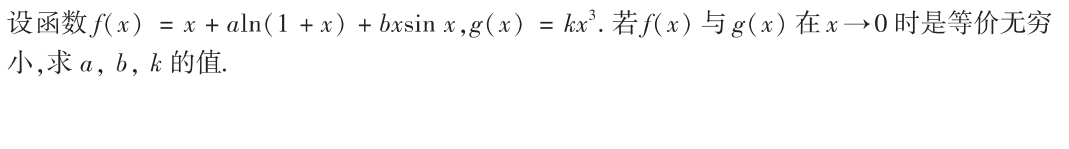
解析:泰勒展开到三阶即可
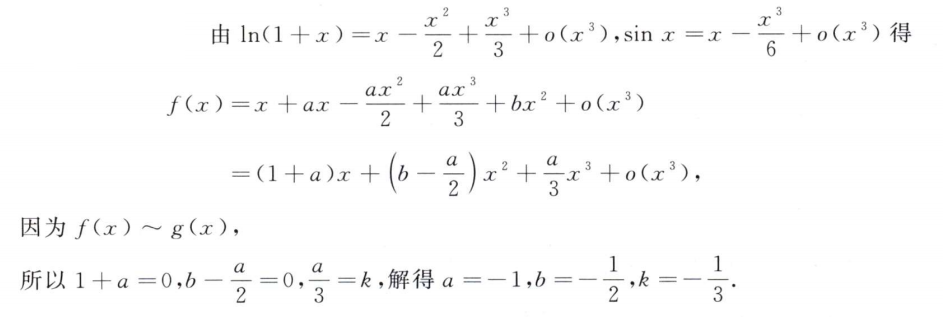
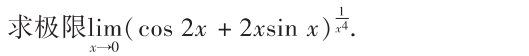
解析:泰勒展开即可
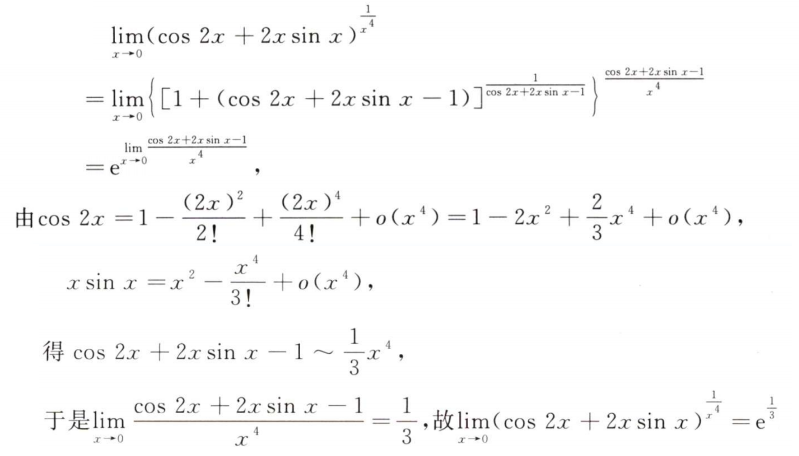

解析:先处理积分,再用洛必达法则
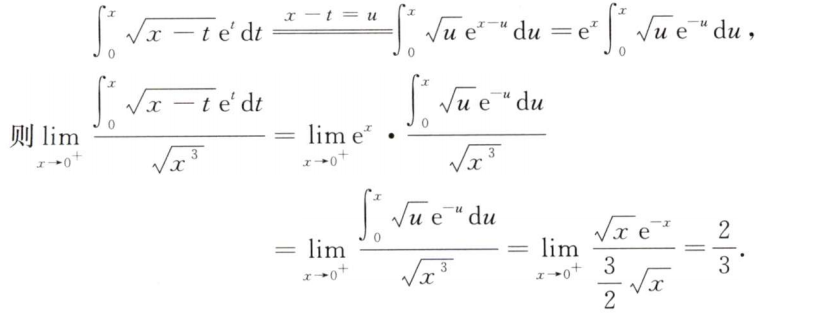
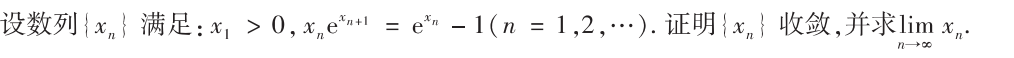
解析:这里用了一个非常很重要的方法,把1代换为$e^{0}$,这样就可以用中值定理,算出$e^{\xi}$,从而知道单调性。并且从0点开始,也暗示了下界

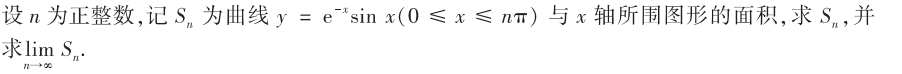
解析:这题非常难,因为$sinx$是周期性函数,所以需要将积分分周期表示出来,最后要根据等比数列求和公式计算出积分
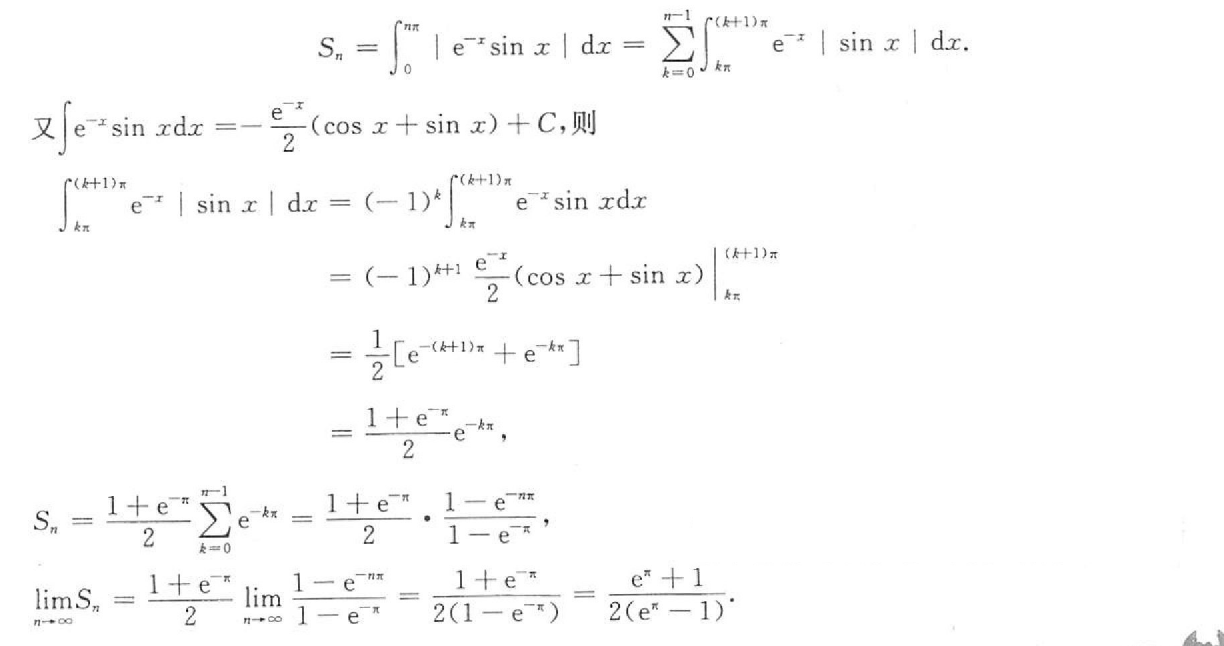
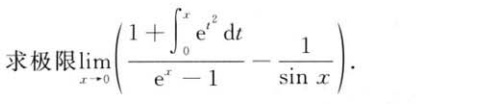
解析:各种方法都行
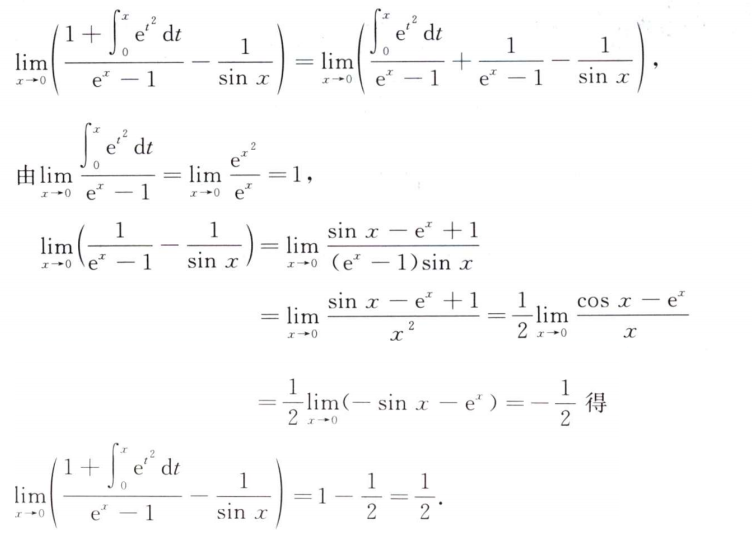
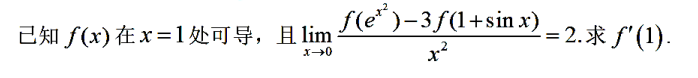
解析:先算出$f(0)=0$,之后用导数定义即可
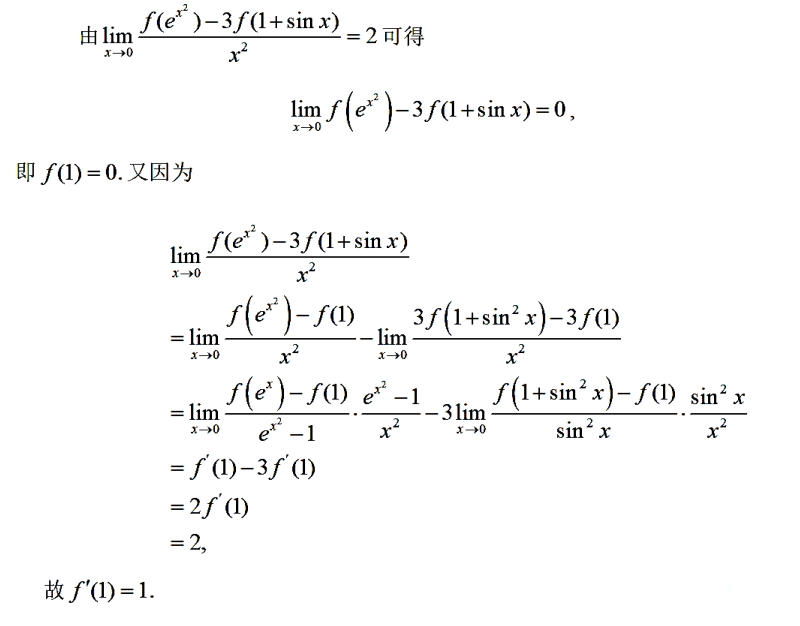
微分学
选

重点在于对曲率圆方程的处理
对方程$x^2+y^2=2$两端对$x$求导,得$2x+2yy’=0,y’(1)=-1$
再求导得$2+2(y’)^2+2yy’’=0,y’’(1)=-2$
所以$f’(1)<0,f’’(1)<0$,$f(x)$在(1,2)上单调减少,无极值
而$f(1)=1>0,f(2)=f’(\xi)+f(1)<f’(1)+1=0$
由零点定理得必有零点,故选B

很常规的一道题: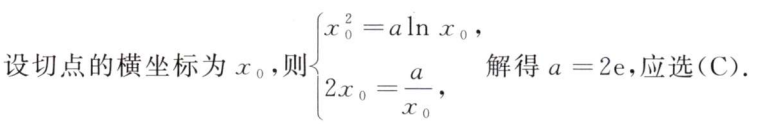

解析:先将$f(x)$拆开后,求导$f’(x)=0$即可得出结论


解析:对$z$求二阶导,要求其二阶导>0,显然选A
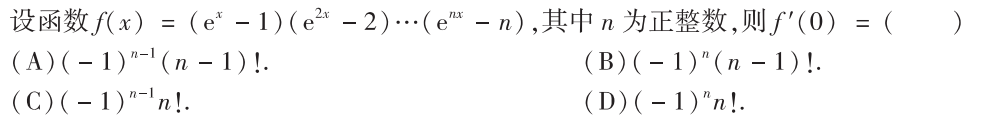
解析:把$f(x)$拆成$(e^x-1)g(x)$即可,选A
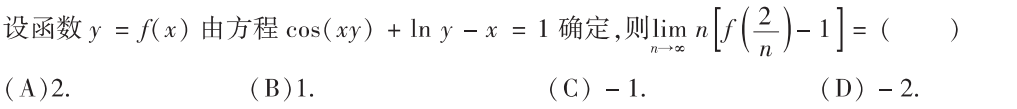
解析:先带入$x=0$算出$f’(0)$,然后用导数定义求解
解析:首先排除水平渐进线和垂直渐进线,逐个验证其斜渐近线,选C
解析:首先注意到$g(1)=f(1)$,$g(0)=f(0)$这个条件,再对两端求导,发现$g‘(x)$是一个常数,即$g(x)$是一条直线,则$f’’(x)>0$时,满足条件,选D

解析:注意是曲率半径$\frac{1}{r}$,而不是曲率
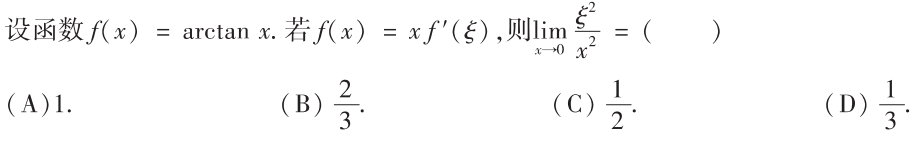
解析:本质上是将$\xi$用$x$表示之后,在等价代换即可


解析:极限为$e^t$,$x=0$时肯定有间断点,可去
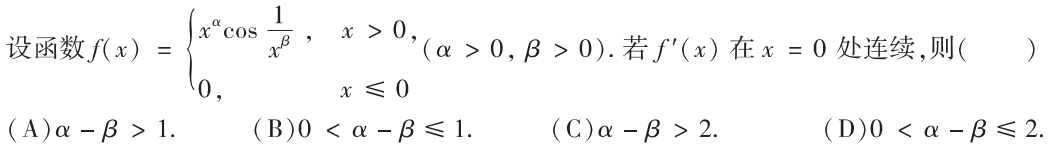
解析:首先是确保$x^a$的$a≥0$才连续,然后$f’(x)$在0点和0点周围要连续
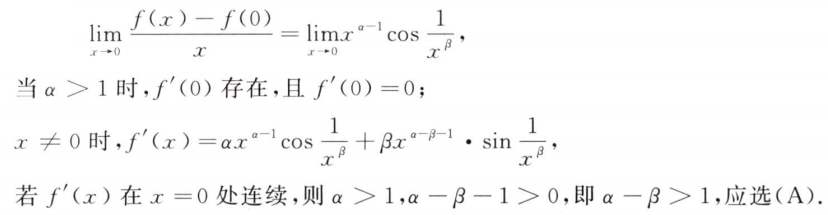

解析:图中正负发生改变的点,即是拐点,所以有2个,选C

解析:图中正负号发生变化的是极值点,零点是拐点,故选B

解析:画图有助于解决此类问题,比较二阶导即可

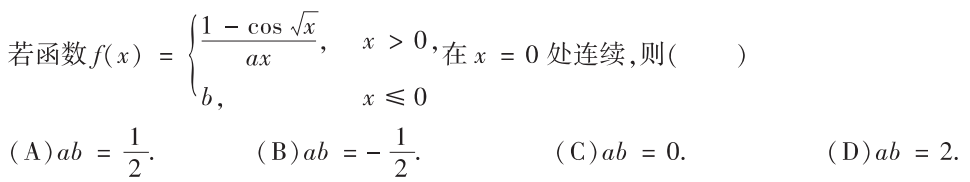
解析:在0点的极限相等

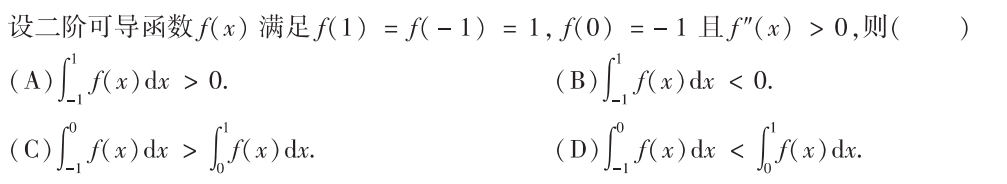
解析:画图可以清晰的看到,积分是小于0的,选B
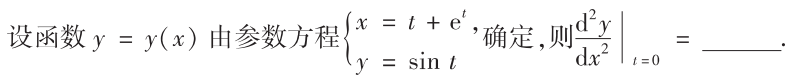
解析:常规题
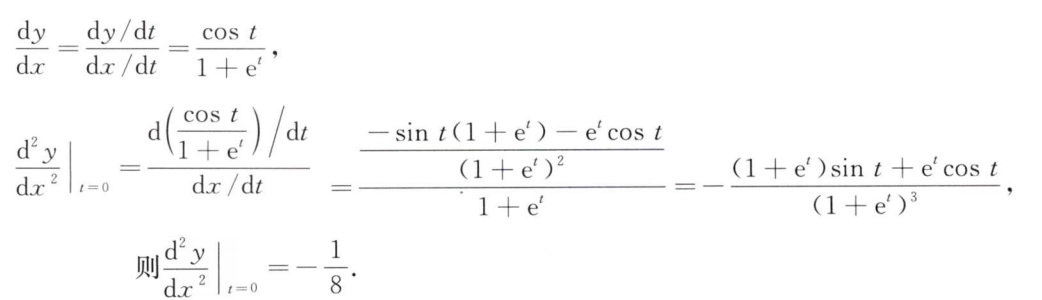

解析:就按定义计算导数

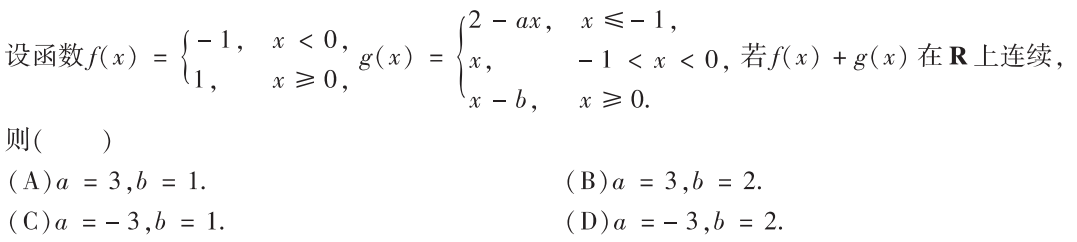
解析:处理好交界点的连续性即可


解析:需要观察,在$x=0$和$x=\pi$的时候都为0,所以需要验证
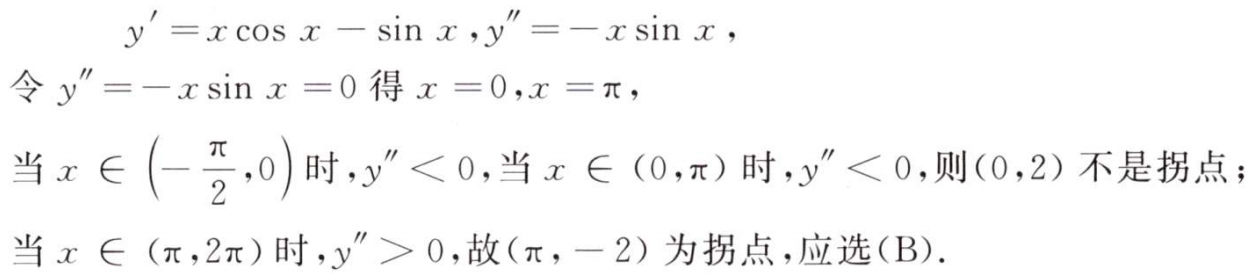

解析:相切且曲率相等的前提是$y’$相等,$|y’’|$也相等,条件可以推出$y’$和$y’’$相等,是充分条件,但是$|y’’|$相等推不出$y’’$相等,所以选A

解析:可能的点有1,2,-1,0四个点,带入计算

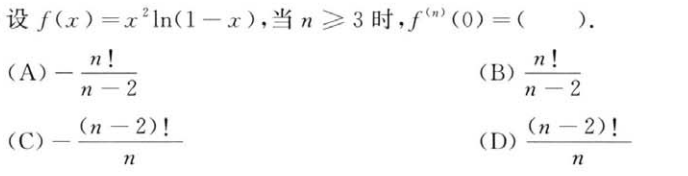
解析:展开$ln(1-x)$的泰勒公式最为简单,也可以求三阶导然后带入
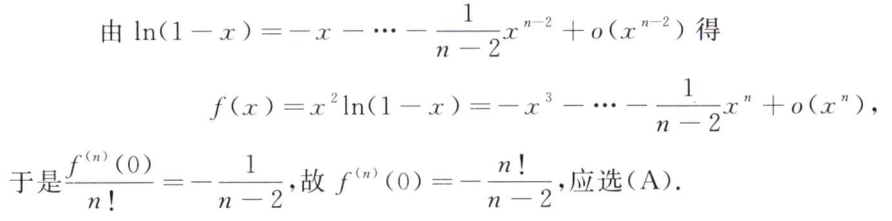

解析:可以假设$f(x)$是$e^{ax}(a>1)$类型的函数,所以只能证明$e^{a}>e$,所以选B

解析:肯定连续,可导要判别$f’(0)$
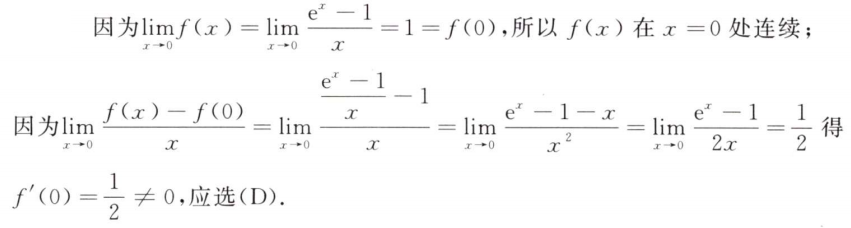

解析:写出体积和表面积的公式,再对半径和高求导,其实是多元函数


解析:将$\frac{b}{a}$设为一个变量,然后画出图形


解析:有二阶导数说明$f’(x)$是连续的,所以能说明在领域内单调增加,选B
填
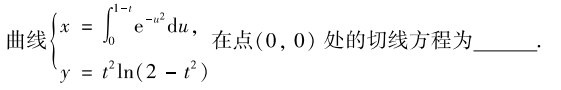
解析:首先要注意:$x=0,y=0$,那么$t=1$,然后分别求导,求出$y’$,最后写出方程

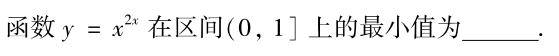
解析:利用对数求导法求出$y’$,然后根据$y’=0$,求出$x$的值,带入即最小值

解析:首先$x=0$,可以求出$y=0$,然后对方程两端求一次导,求出$y’$,然后再求一次导,带入$x,y,y’,$即可求出$y’’$


解析:首先排除水平渐进线和垂直渐近线,可以计算出a和b的值
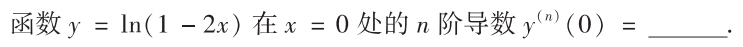
解析:对$ln(1-2x)$求导以归纳规律
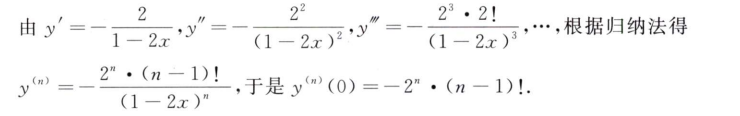
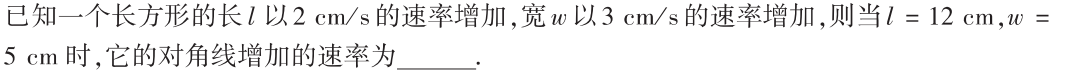
解析:首先写出对角线关于$l$和$w$的方程,然后再求导,即是对角线增加的速率
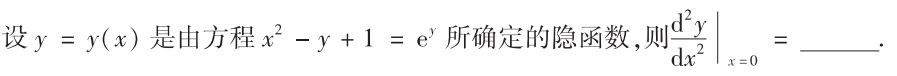
解析:对方程求二次导即可


解析:将x,y地位互换
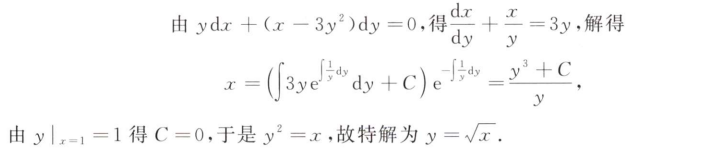

解析:带入公式可计算:


解析:由$y$的值推出$x$的值
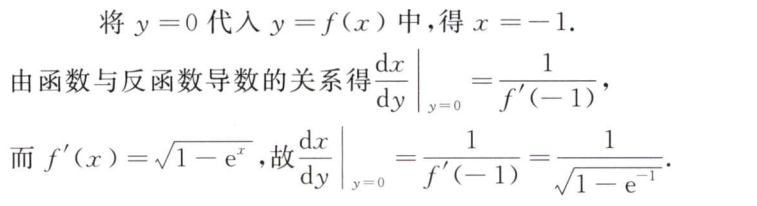
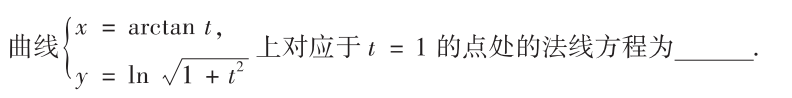
常规题

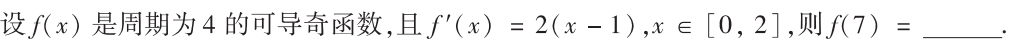
解析:常规题
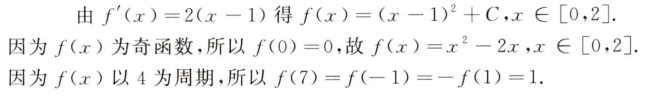
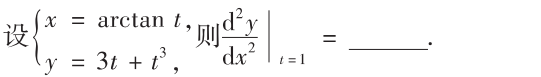
解析:常规题
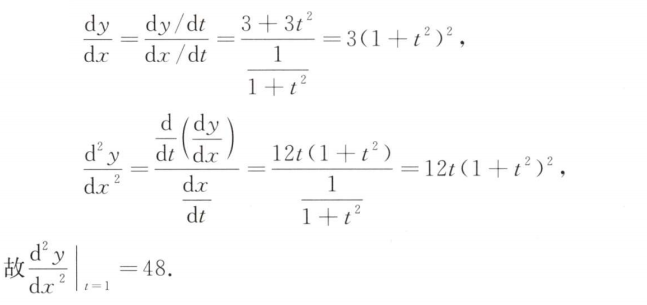
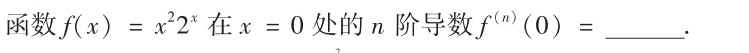
解析:多项式定理
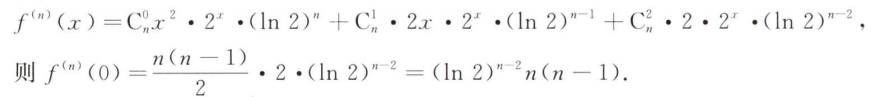

解析:常规题

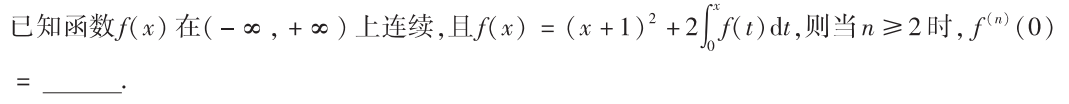
解析:归纳法


解析:先列出$v_0$和$l$的关系,在求导算出变化率
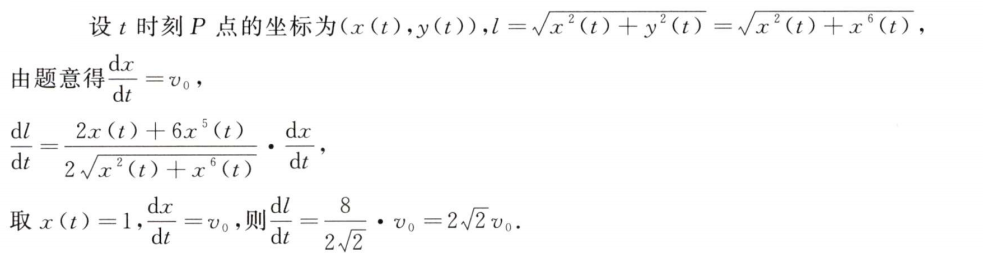

解析:常规题
解析:常规题
解析:求出$y’$和$y’’$即可
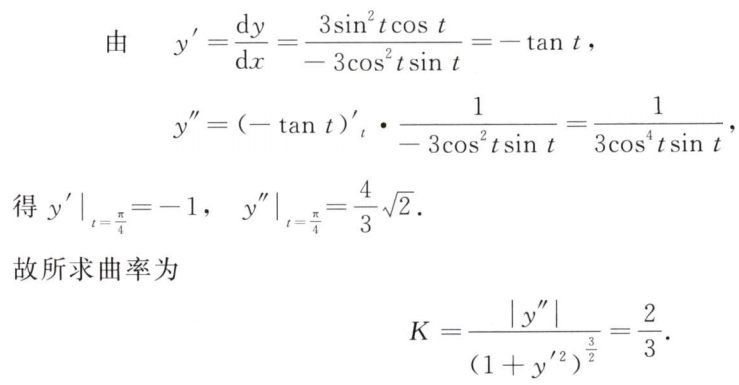

解析:求出斜率,找到点,列方程,求截距

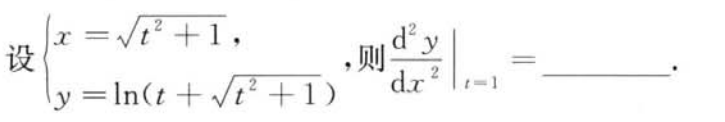
解析:常规题
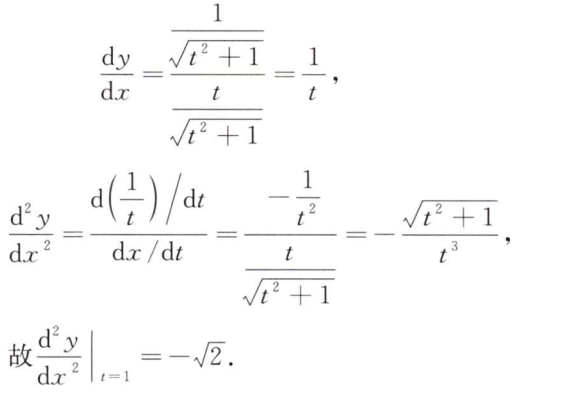
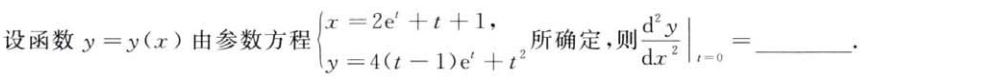
解析:
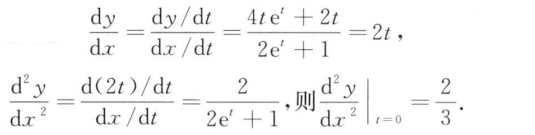
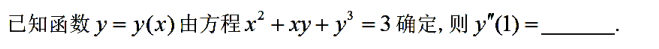
解析:
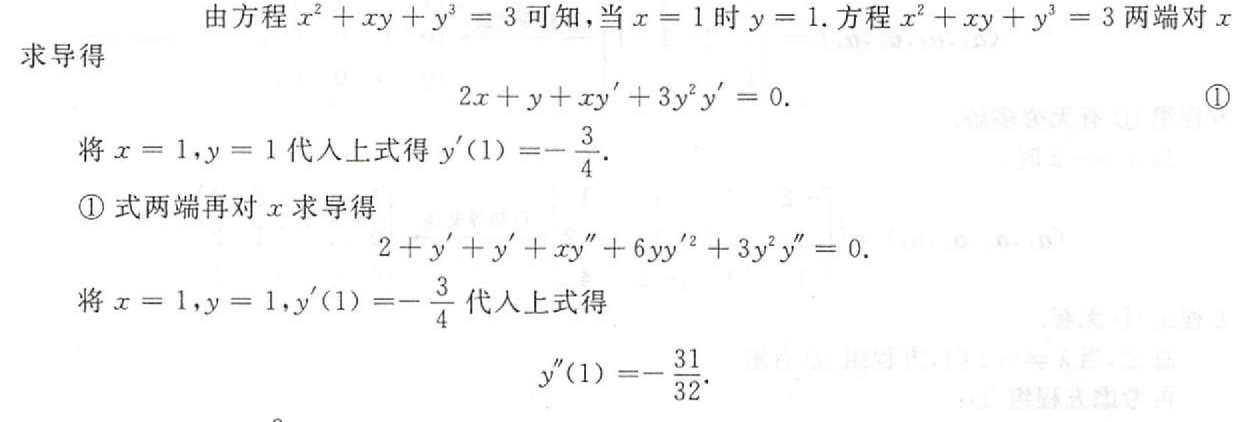
综
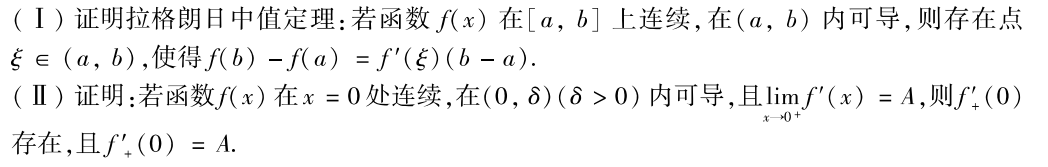
引进辅助函数即可证明:
因为$F(a)=F(b)$,由罗尔定理$F’(\xi)=0$,即可证明拉格朗日定理

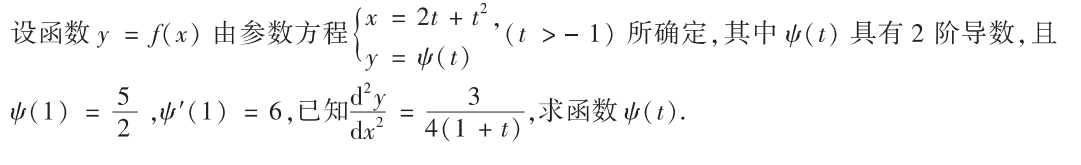
解析:本质是微分方程求解,$\psi(1)$和$\psi’(1)$都是条件

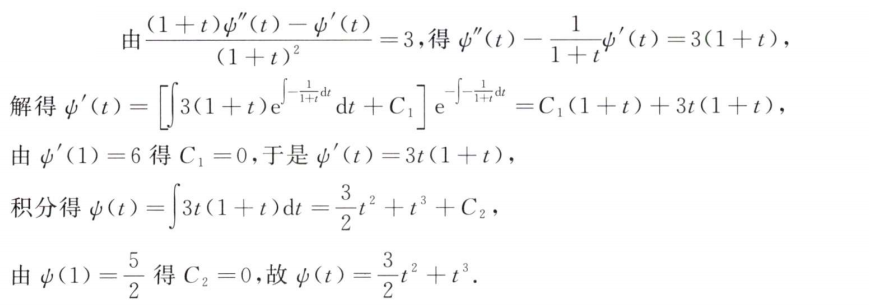

解析:设原函数$F(x)=f(x)-\frac{x^3}{3}$,用微分中值定理即可证明
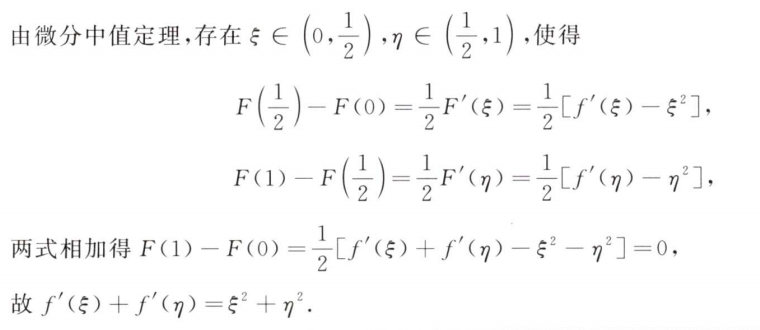
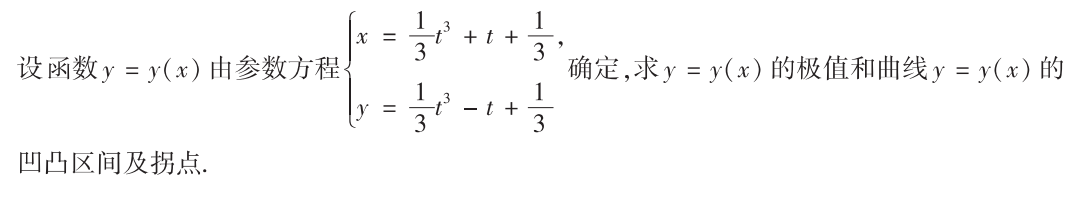
解析:常规题,特别要注意的是算出$t$的值后,要把$x,y$的值也带入算出来

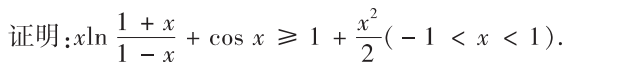
解析:组成一个新的函数,求其最小值大于等于0即可


解析:奇函数隐含$f(0)=0$,第1问用拉格朗日定理即可
第2问需要设置$F(x)$


解析:求出$x_0$后,用拉格朗日定理可以很好求解

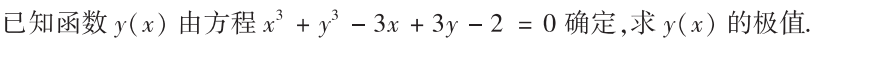
解析:$y’=0$求出可能的$x$的点,然后求出$y$的值,再求$y’’$的值来判断极大或极小


解析:问1可由保号性证明,而问2的关键在于判断出原函数后,证明3点同值即可


解析:利用条件列出微分方程,然后求解

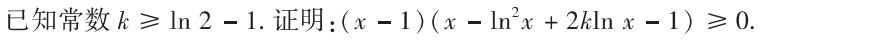
解析:$k$单独表示,然后求导


解析:先求解出用$P$点$x$表示$S$的面积,再对$x$求导,即是$S$的变化率

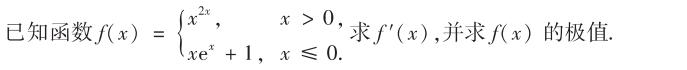
解析:尤其注意连接点的导数
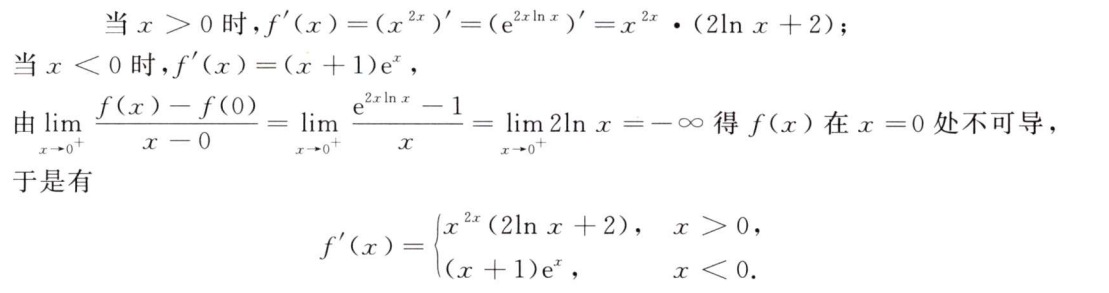

解析:用待定系数法做,注意$x^2+x+1$对应的系数我$Ax+B$

解析:第1问由积分中值定理+拉格朗日中值定理可证,第2问需要假设出原函数后,反复用中值定理
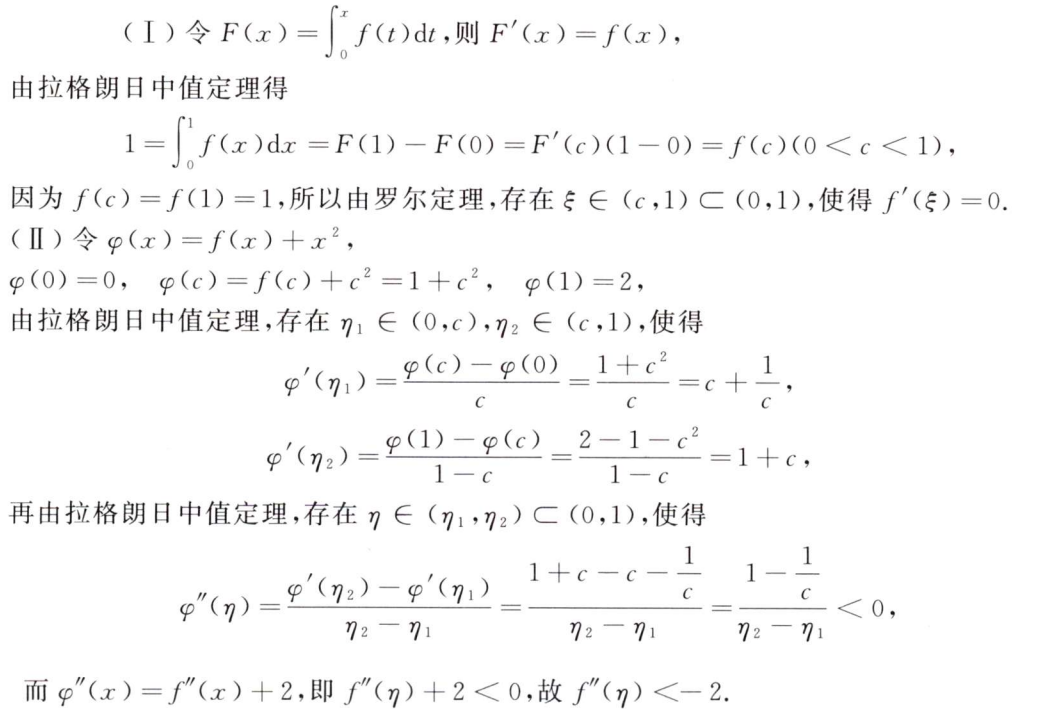

解析:第1问用零点定理好证明,第2问,需要看出$ln1$和$f(1)$都为0,所以是用柯西中值定理
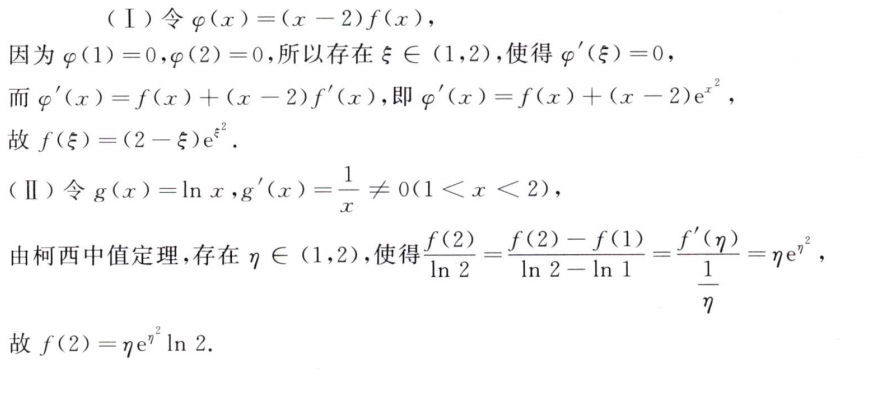

解析:


解析:必要性的证明方法在之前的选择题中有所体现
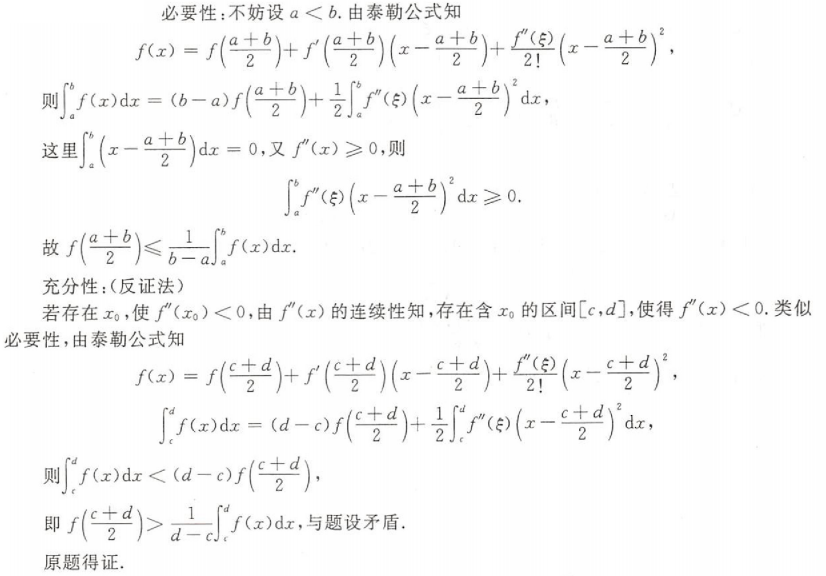
积分学
选
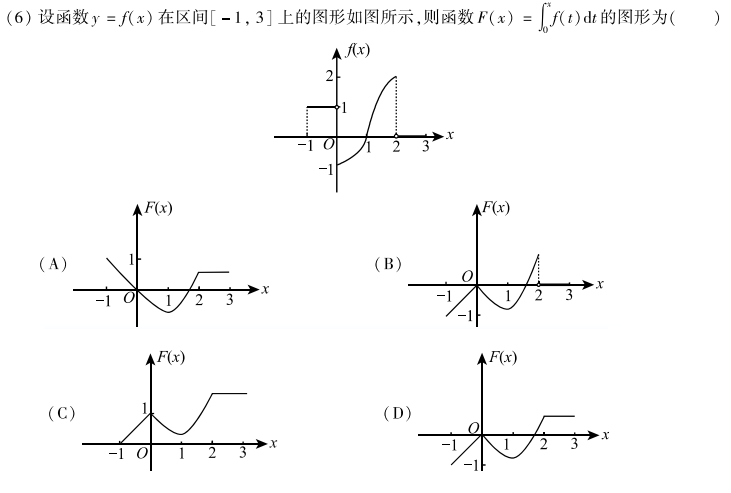
解析:在$[-1,0]$阶段,$f(x)=1$,显然是$y=x$曲线,所以排除AC
而在$[2,3]$时,$f(x)=0$,所以$F(x)$的值不会在$[2,3]$增长,选D
解析:有两个暇点需要讨论,在$x\to 0$时比较好计算,而在$x\to1$ 时需要用到比较审敛法

解析:在$[0,\frac{\pi}{4}]$区间,显然$sinx
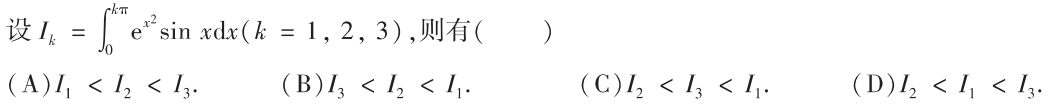
解析:该题的被积函数一样,积分区域不一样,所以用让积分相减比大小
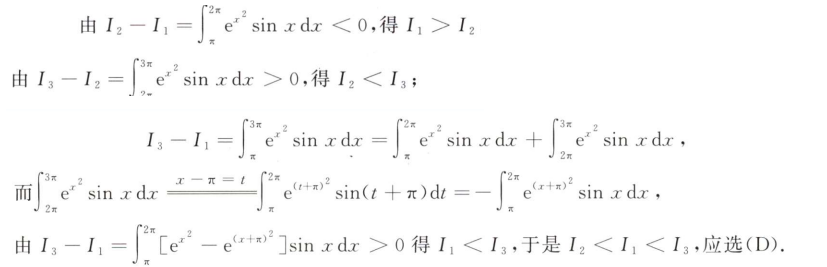
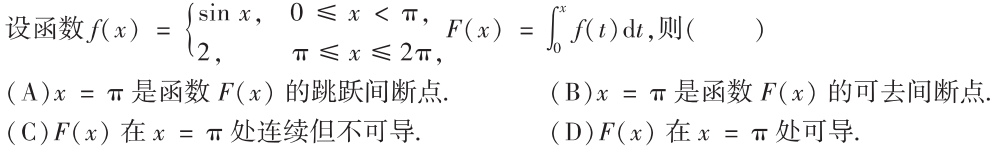
解析:根据总结的上限积分规律,$x=\pi$ 是$f(x)$的跳跃间断点,则$F(x)$连续但不可导,选C

解析:从两个方向考虑:

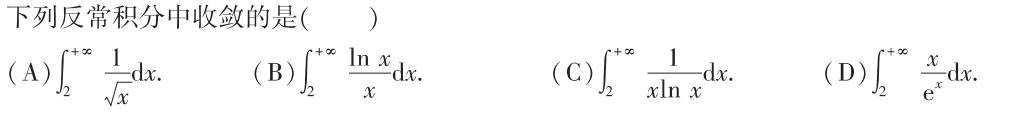
解系:可以逐个计算,结果选D

解析:首先原函数要连续,其次,导数为$lnx$,选D

解析:很明显会在$t=25$的时候追上
重点:对泰勒公式进行积分的思路令人眼前一亮
解析:

解析:找到了$M=\pi$的中间桥梁
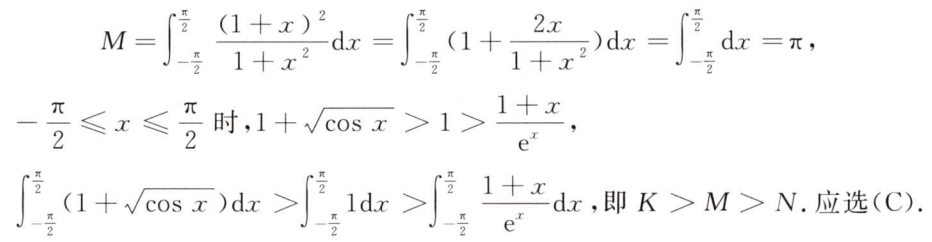
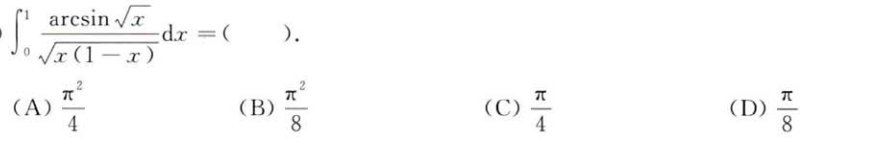
解析:熟悉$arcsinx$的导数即可
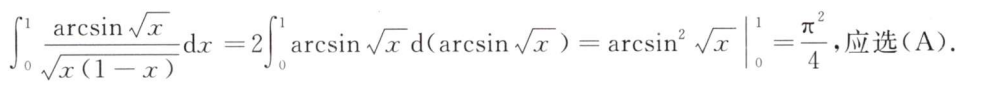

解析:如果是$\frac{1}{n}$,那么里面也要被分成$n$份,只有B符合条件
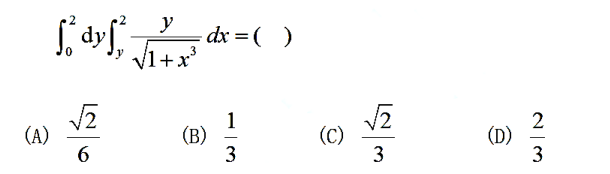
解析:更改次序后方便计算
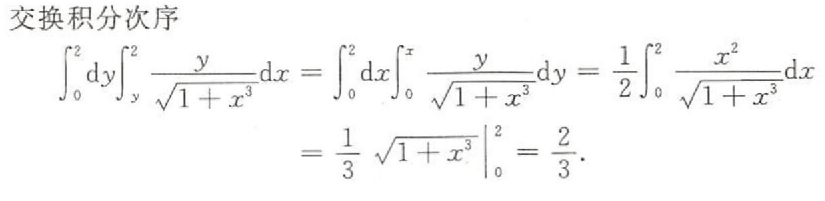
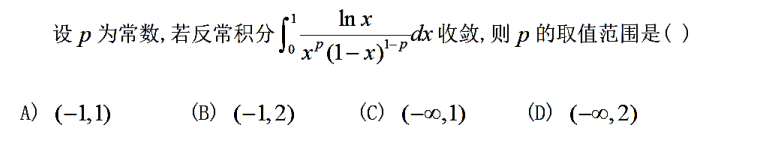
解析:直接带1进去,发现$p≠1$,排除B和D,在$x\to 1$的时候,$lnx\sim 1-x$,所以$-p<1,p>-1$选A
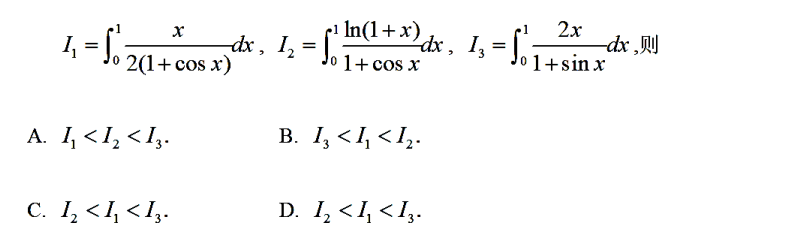
解析:$ln(1+x)>\frac{x}{2}$,$I_2>I_1$,而$1+sinx<1+cosx ,2x>ln(1+x)$,所以$I_3>I_2$,选A
填
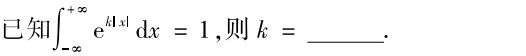
解析:积分函数是偶函数,同时积分区间关于原点对称,所以可以算$[0,+\infty]$积分即可
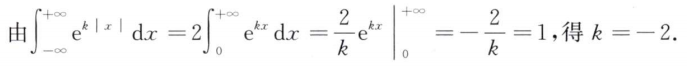
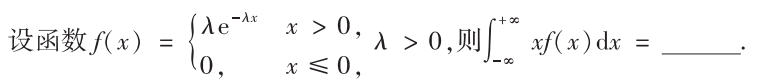
解析:拆成$[-\infty,0]$和$[0,+\infty]$两个区间,$x<0$时为0,$x>0$时,积分为$\frac{1}{\lambda}\int_0^{+\infty}te^{-t}dt=\frac{1}{\lambda}$,所以答案为$\frac{1}{\lambda}$
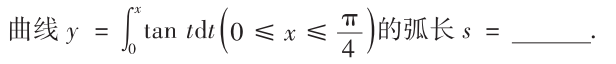
解析:先用弧长公式,再用积分公式可得结论
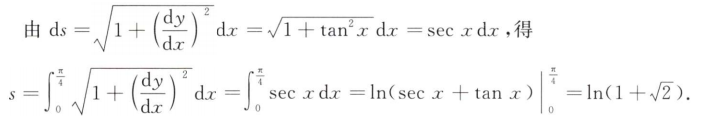
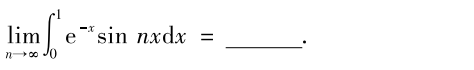
解析:主要就是考察分部积分法的计算,属于是纯计算问题,按优先级先将$sinnx$积进去
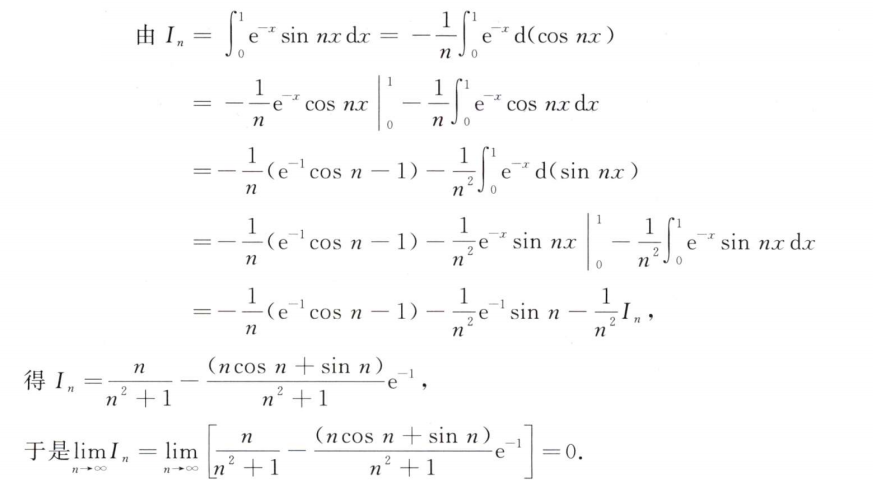
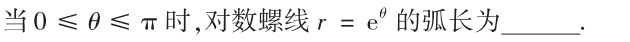
根据极坐标方程的弧长公式可轻松求解
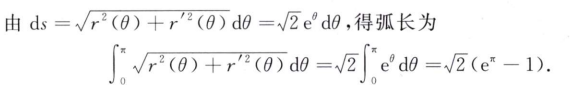
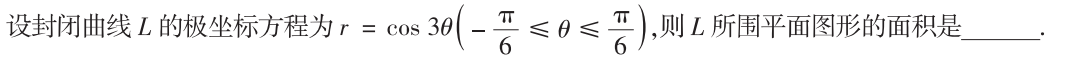
解析:和之前的$r=1+cos\theta$的题很相似,注意要乘上$r$

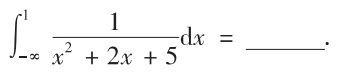
解析:
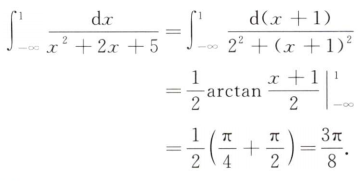
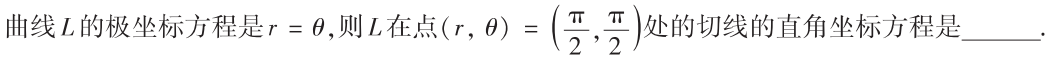
解析:转化为$x,y$,并根据参数方程的形式求出$y’$
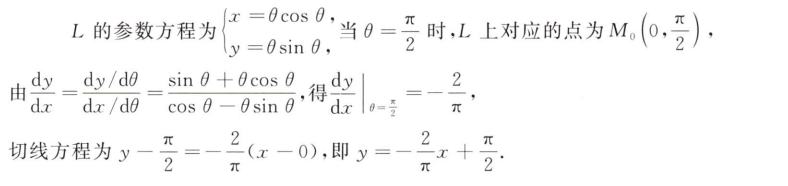
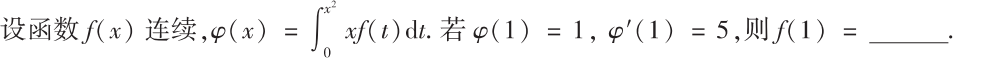
解析:常规题
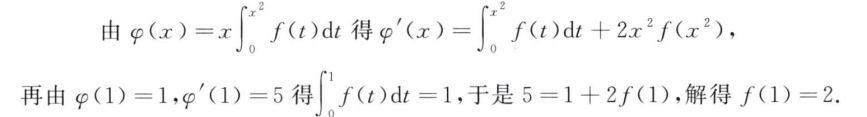
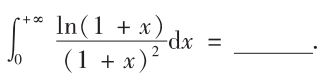
解析:分部积分法:
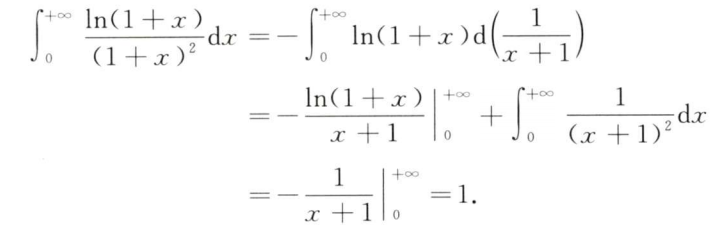
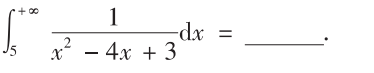
解析:直接拆开即可
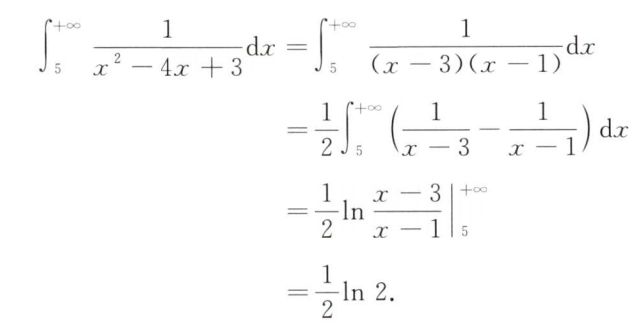
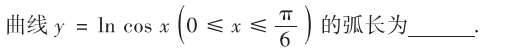
解析:
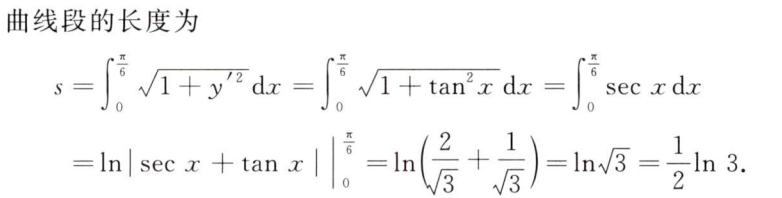
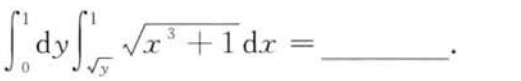
解析:交换积分次序
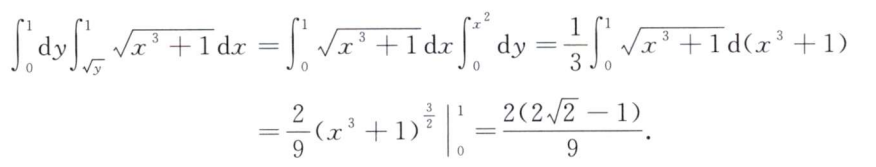

解析:画出图后,用微元法分析:
其中积分距离是$x$,而因为是等腰三角形,积分区域=$2(a-x)$

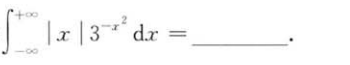
解析:
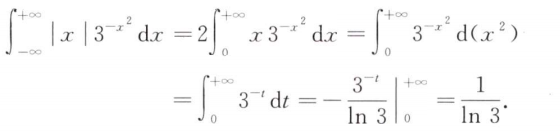
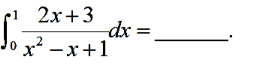
解析:
综
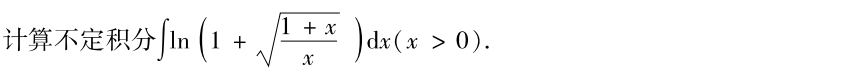
首先将根式化为$t$,然后正好用分部积分法,然后用待定系数法求解积分即可,最后结果记得$+C$
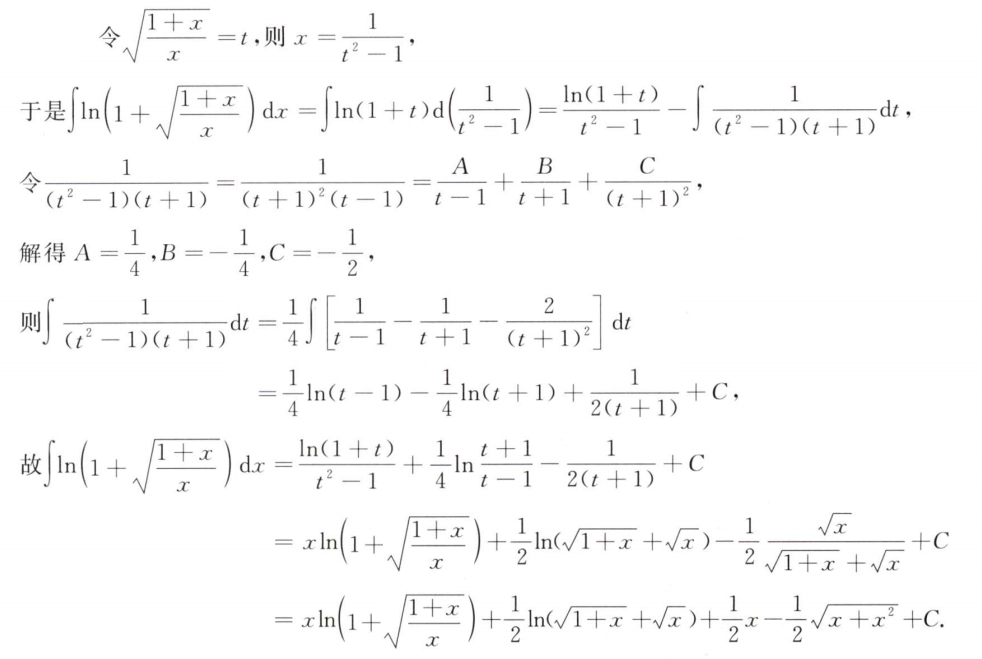
解析:先对函数$f(x)$求导,然后根据$f’(x)=0$的点判断单调区间与极值
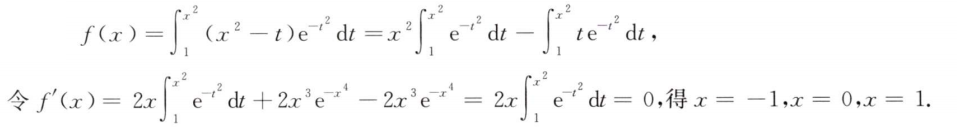

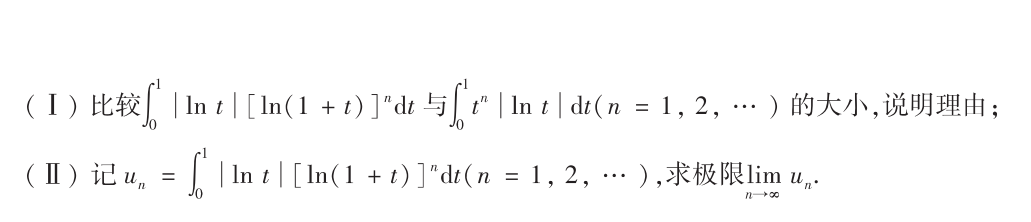
解析:显然$t>ln(1+t)$,所以第一问易证,证明出第一问的结论后,直接夹逼定理可得出极限

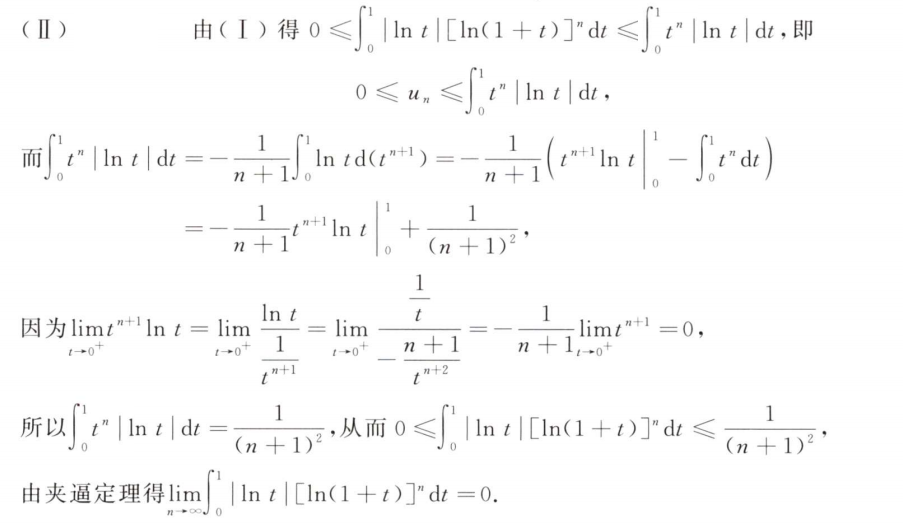

解析:此题实际上就是其阴影部分面积,下半部分椭圆面积为$\frac{1}{2}\pi ab$,而上半部分的面积需要用定积分计算
首先椭圆的公式为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,将$y$用$x$表示,最后将$y=bsinx$代换即可算出上半部分面积


解析:第1问用积分中值定理易证,第2问用单调性
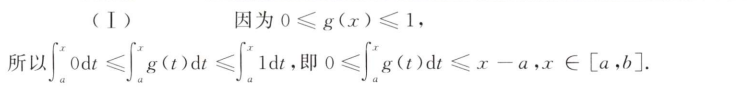
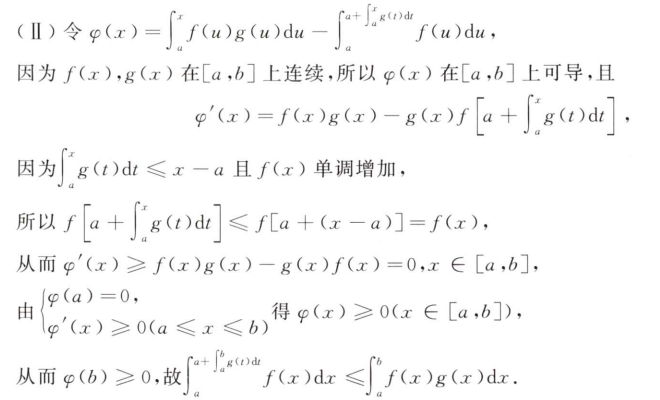
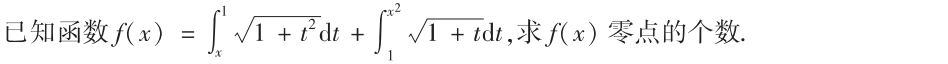
解析:不需要算出具体的值,只需要判断>0or<0即可
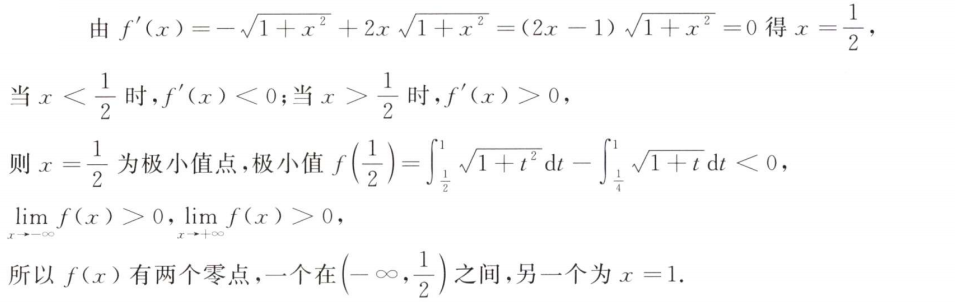
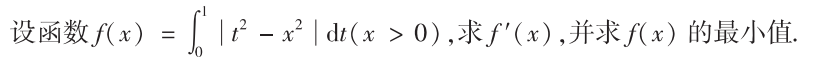
解析:对$x$的取值分类讨论
解析:根式设为$t$即可


解析:其实是一个微分方程


解析:计算量大

常微分
选

解析:分别将$\lambda y_1+\mu y_2$和$\lambda y_1-\mu y_2$带入方程,即可得到$\lambda+\mu=1,\lambda=\mu$的结论,故选A
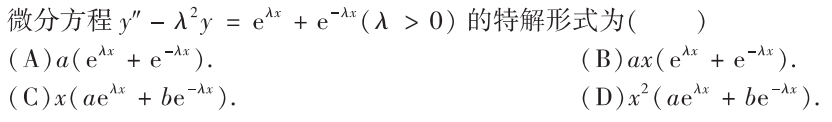
解析:$\lambda$ 和 $-\lambda$就是特征方程的两个解,根据叠加原理,答案为C

解析:算出$r$,然后设特解

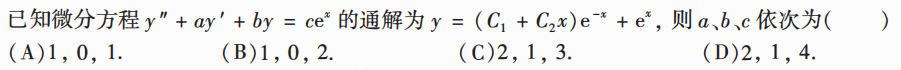
解析:说明有齐次方程是$r=-1$的重根,算出齐次方程后带入$e^x$解出c

解析:
填
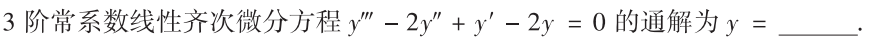
直接列特征方程然后拆项,$(r-2)(r^2+1)=0$,故可以写出通解$C_1e^{2x}+C_2sinx+C_3cosx$
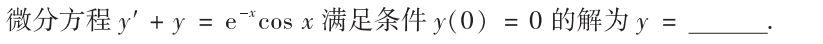
解析:直接带入公式即可得到,$y=e^{-x}sinx$

解析:可以看出$e^x$和$e^{3x}$是齐次解,而$-xe^{2x}$是特解,根据条件解出$C$即可
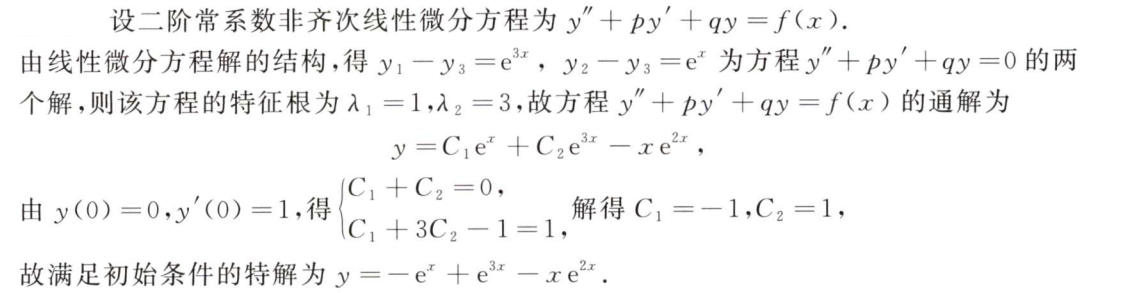

解析:先相减算出齐次方程的通解,求出齐次方程后,带入特解,求出其他项
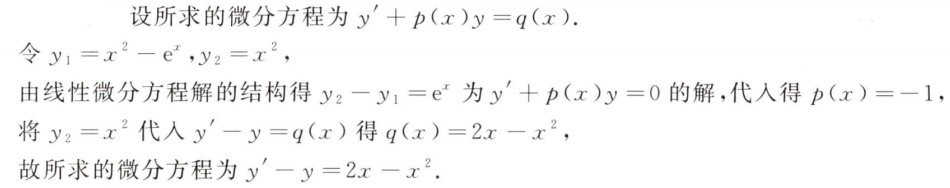
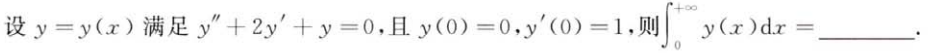
解析:算出$y$后,进行积分即可

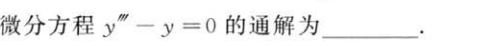
解析:写出微分方程,然后根据重根写出通解

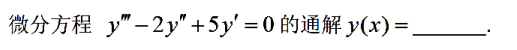
解析:
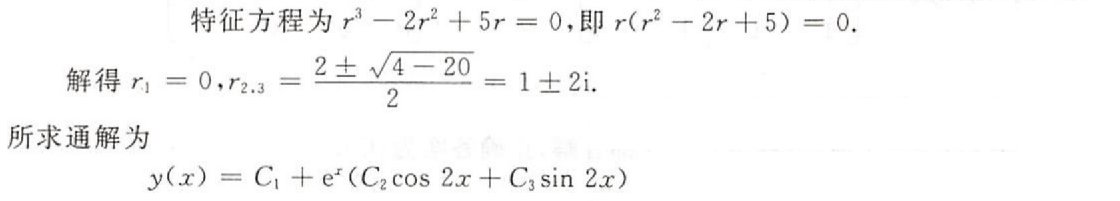
综

解析:本题隐含了很多条件:光滑曲线$\implies$ 曲线连续且在连接处导数连续
首先将曲线分成两段来算,在$[-\pi,0]$段,列出法线方程,就可以得到一个微分方程并解出
在$[0,\pi]$段,可以直接求解方程,加上光滑曲线这一隐含条件$y(0)$和$y’(0)$都要一致,求出完整方程

注意法线方程的写法,$YX$表示的是变量,而$yx$表示的是曲线上某个点

解析:$tana=\frac{dy}{dx}$,对该式两边求导得出微分方程

注意$\int cot dx=ln|sinx|+C$
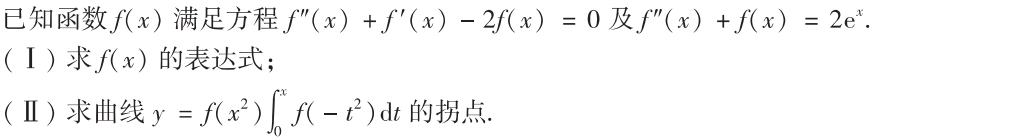
求出$f(x)$后带入求$y’’=0$,猜出点即可
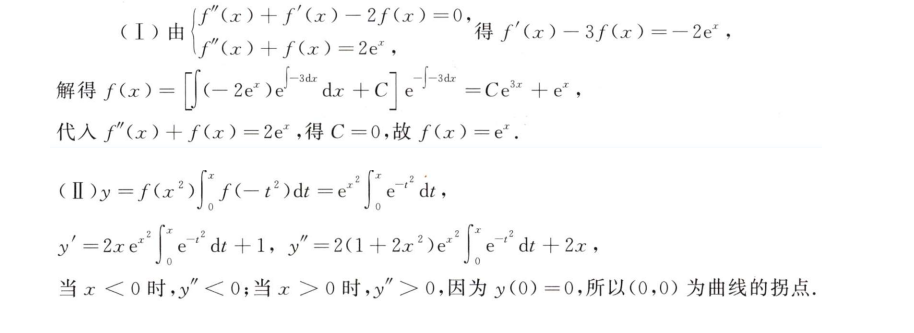
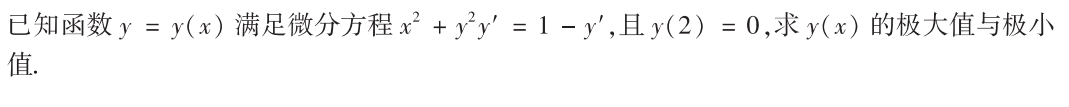
解析:


解析:很经典的题,主要是要将变化率设为$-k$,$y’=-k(y-20)$,虽然算式中没有$x$,但是最终的结果和微分方程一样,会有$x$


解析:计算量很大,将$u(x)e^x$带入方程中创造出另外一个微分方程


解析:解微分方程算出$y(x)$,之后轻松算出$V$
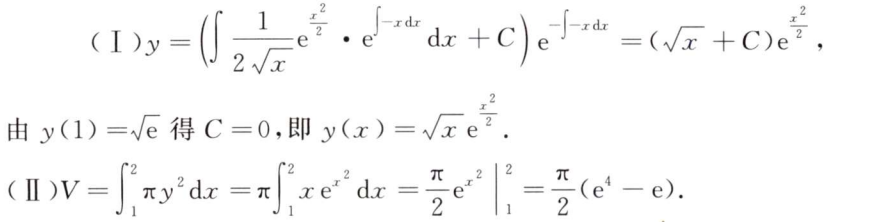

解析:把$\frac{1}{x}$和$x$互换写出微分方程,然后解微分方程
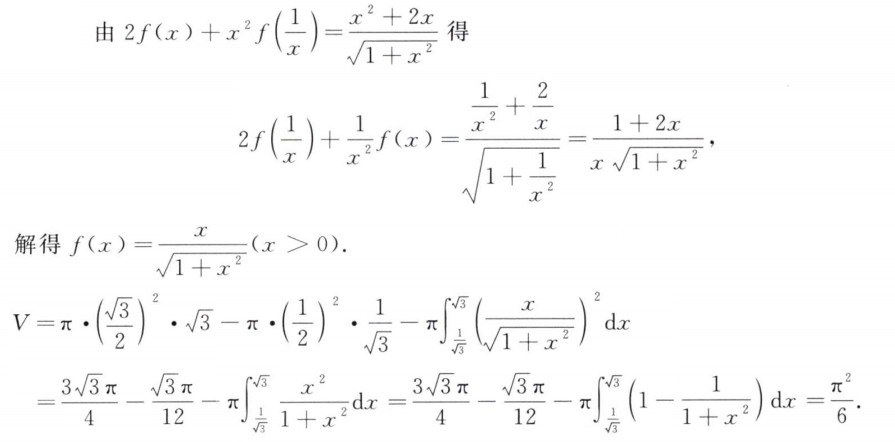

解析:

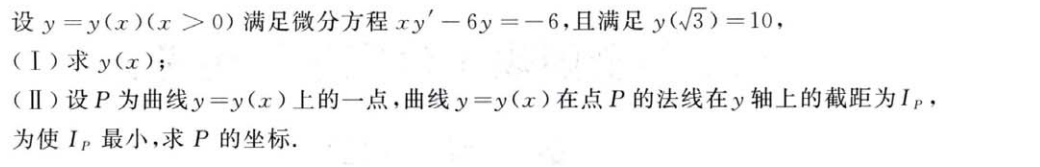
解析:单纯计算量大

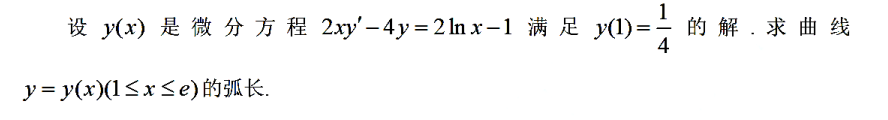
解析:常规题
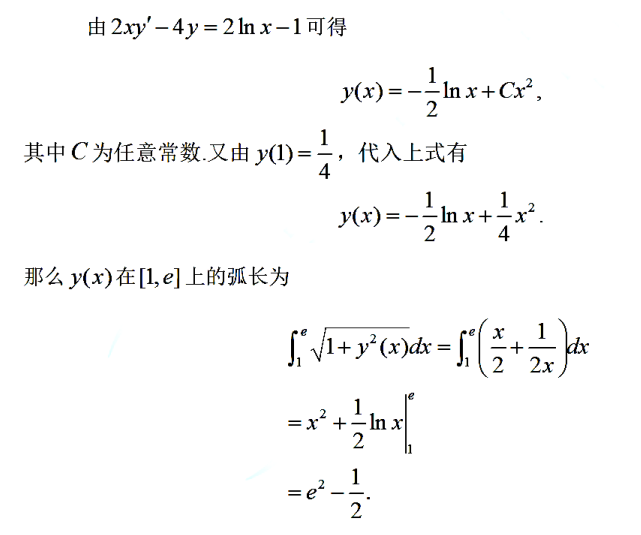
多元微分
选
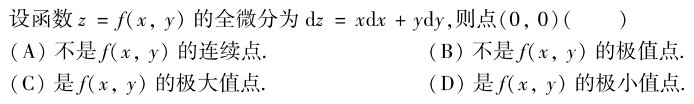
解析:$dx$前面就是$x$的偏微分,$dy$前面是$y$的偏微分,所以(0,0)这个点是极小值,选D

重点是求偏导
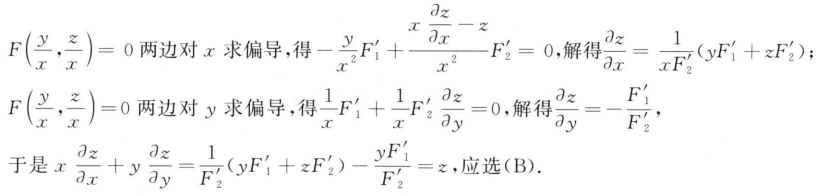
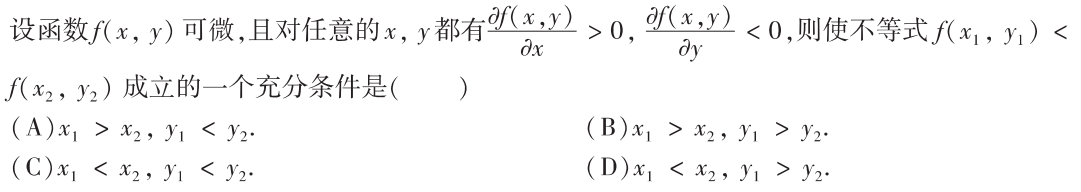
解析:当成两个一元函数即可,选D
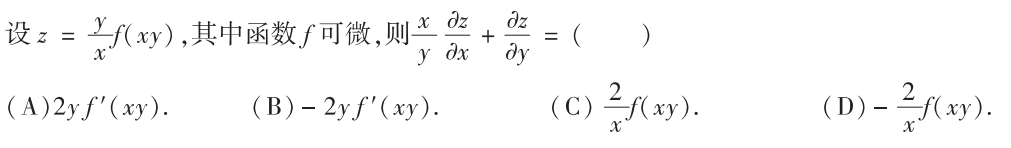
解析:常规计算
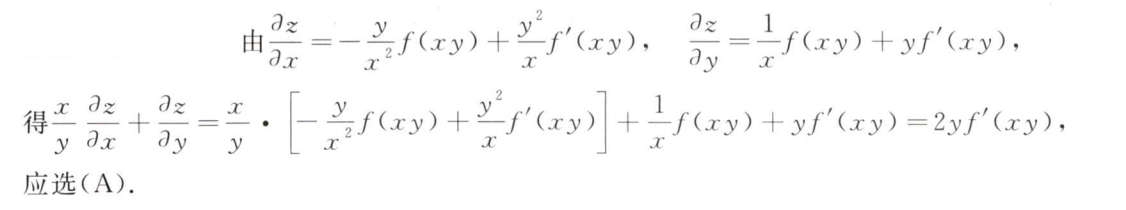

解析:$f_{xx}×f_{yy}$必<0,而$f_{xy}×f_{yx}$必>0,故内部无最大最小值,选A
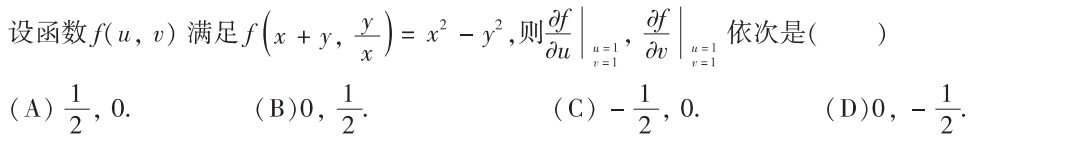
解析:将$x,y$用$u,v$表示

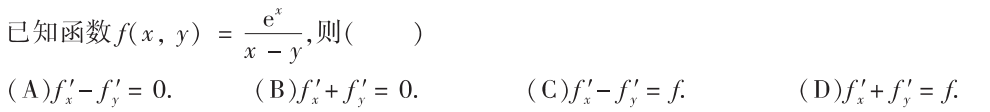
解析:基础题
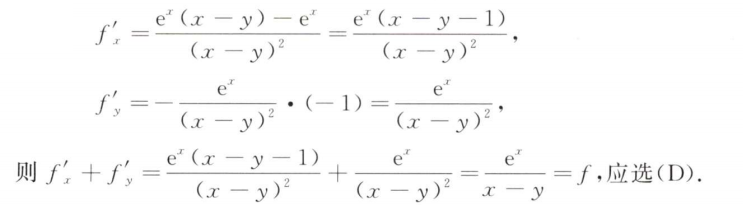

解析:显然$x$单增,$y$单减,所以选D

解析:除了2,其他都对

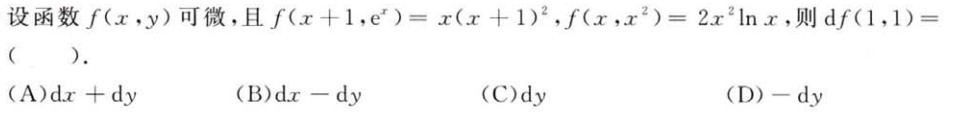
解析:写出$f(x,y)$的表达式即可

填

解析:方程两边求导即可:
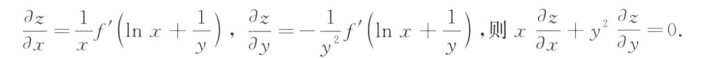
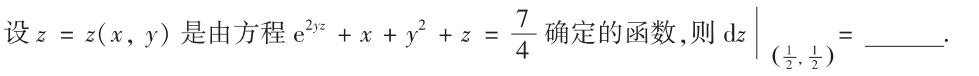
解析:先算出$z$,然后分别对$x$和$y$求偏导

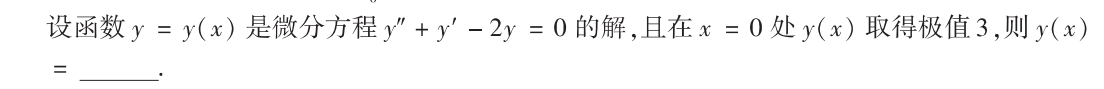
解析:常规题

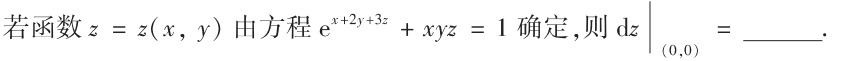
解析:分别求偏导即可

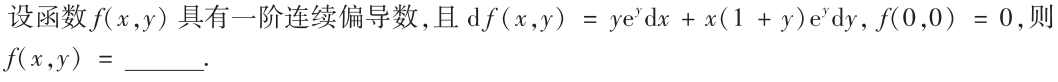
解析:根据$x,y$的偏导推出$f(x,y)$
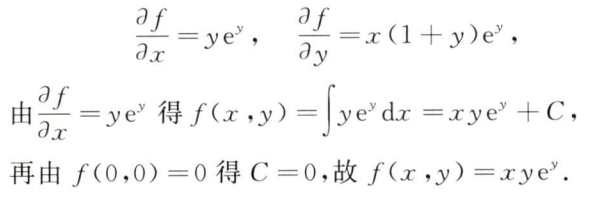
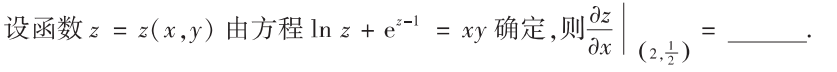
解析:对$x$求偏导数再代入即可

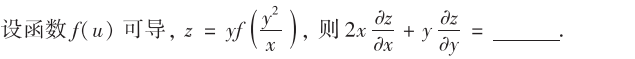
解析:常规题
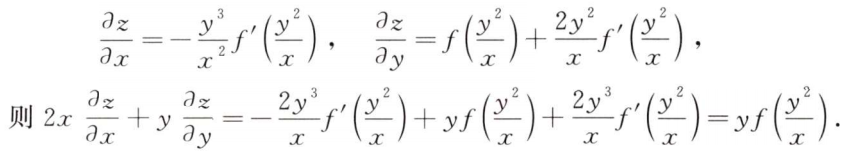
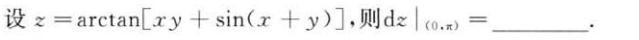
解析:先代后求,简化运算
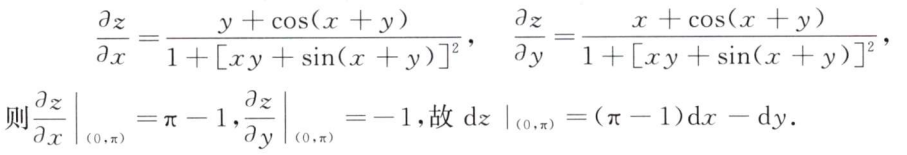

解析:常规题

综
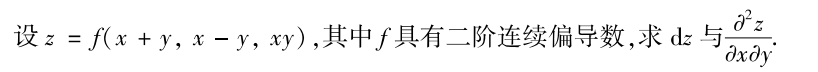
解析:分别求出$x$和$y$的偏微分即可求出$dz$,而对$x$的偏微分再对$y$求导即可得出答案
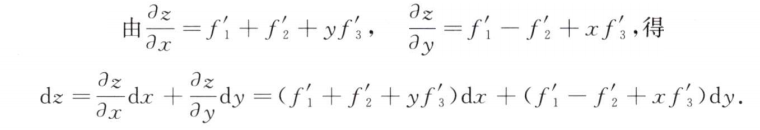
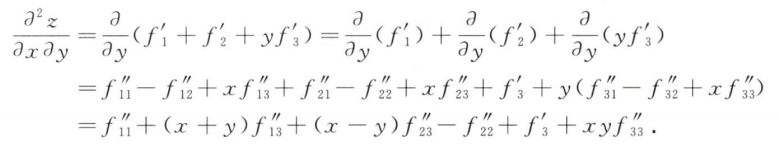

解析:将$x$和$y$分别用$\xi$和$\eta$表示,然后简化
结果过于复杂,莫名奇妙

解析:常规题
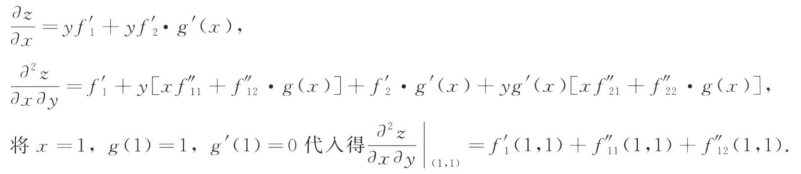
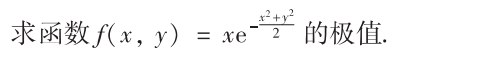
解析:先确定关于x和y的偏导数为0
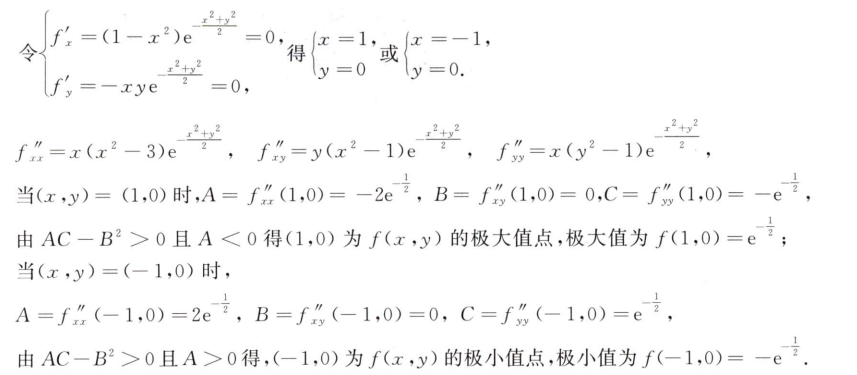
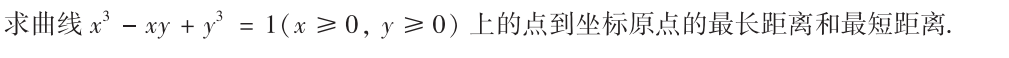
解析:可以设$z=x^2+y^2$,用拉格朗日乘数法来计算,同时注意曲线的端点


解析:
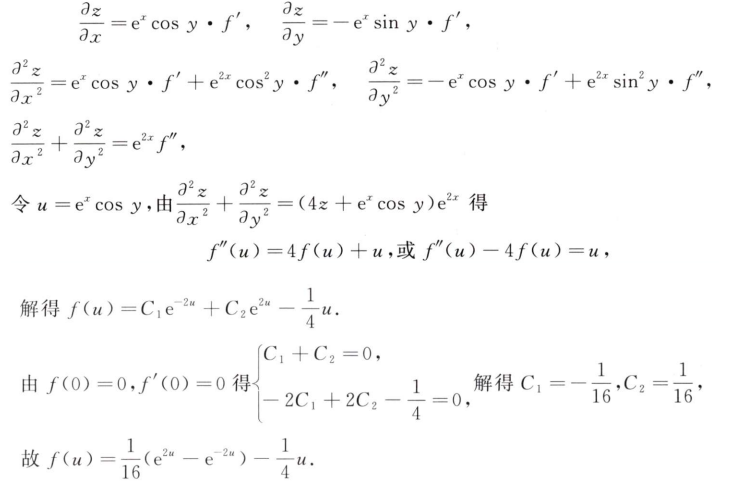
解析:根据条件求出$f(x,y)$,再求极值
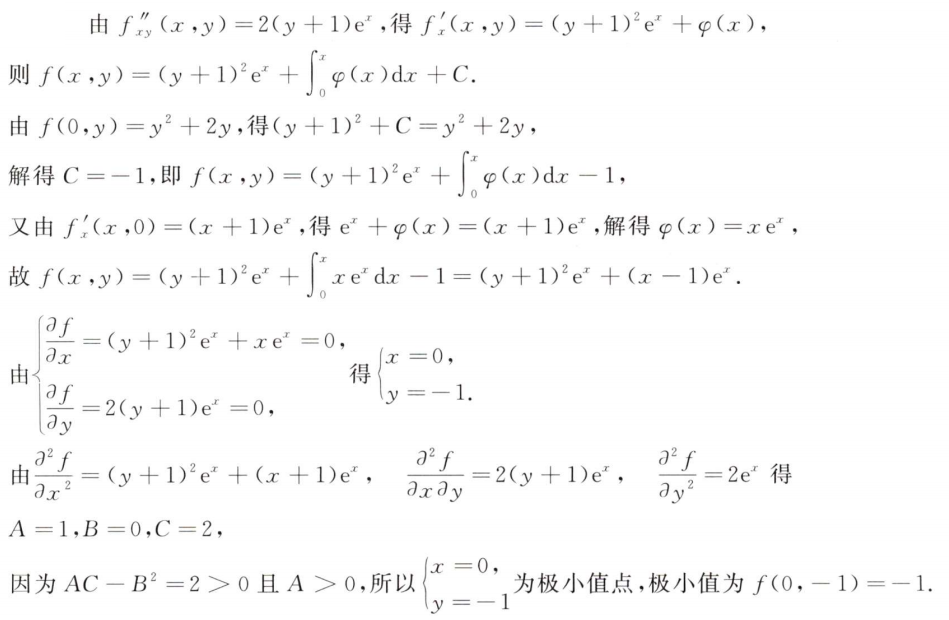
解析:算出$x,y,z$的关系,将其统一为一个一元方程,算出具体的点

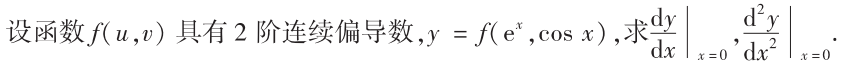
解析:常规题

解析:题目不难,计算量极大,分给圆的长度为$x$,给正方形$y$,给三角形$z$,$x+y=z=2$ 用拉格朗日乘数法求解



解析:题目不难,计算复杂
解析:常规题

解析:

多元积分
选
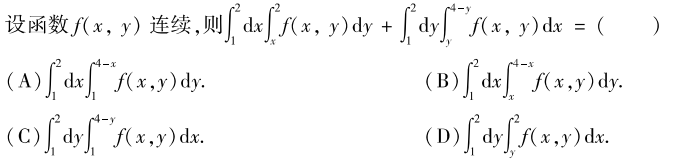
画出积分区域:
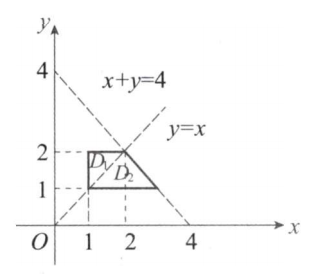
选C

解析:根据定积分的定义,选D
解析:根据对称性,实际上就是算图形的面积
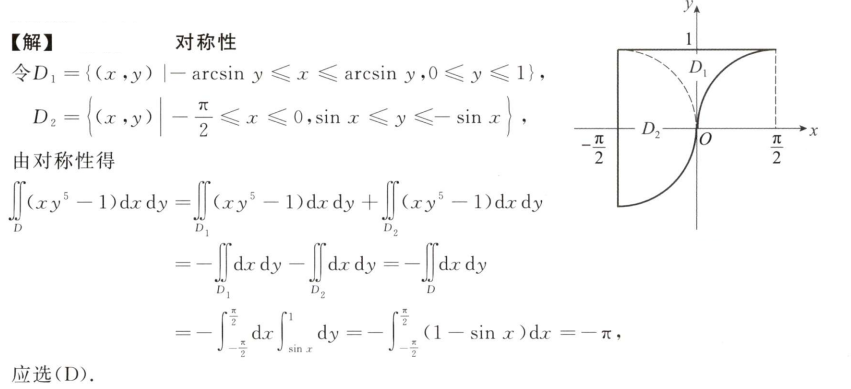

解析:画出积分区域,在$y>0,x<0$的情况下能保证最后的结果>0,选B

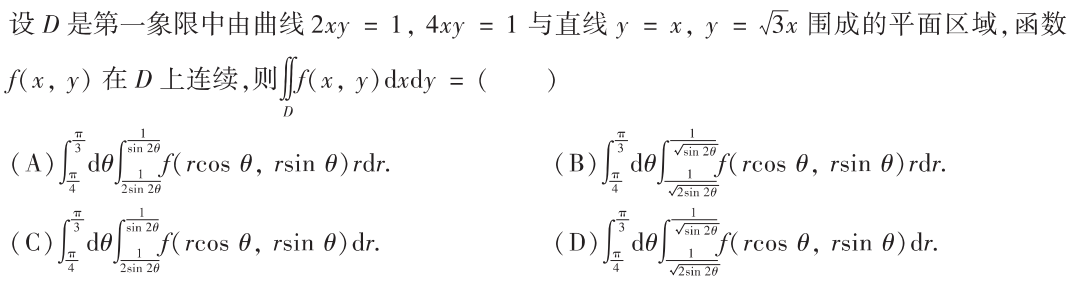
解析:甚至不需要画出积分区域即可做出来,选B
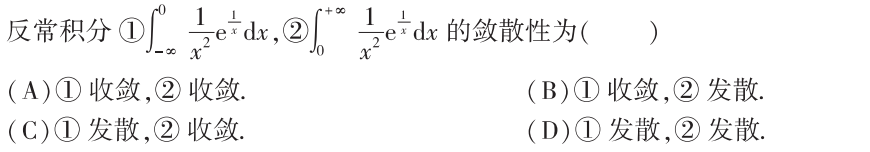
解析:从$0^{-}$逼近和从$0^{+}$逼近是不同的
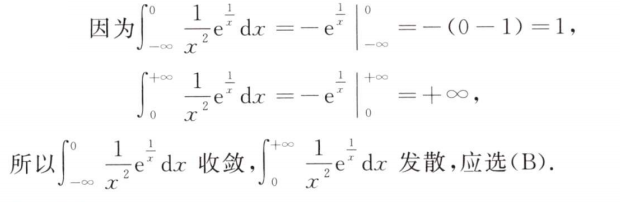
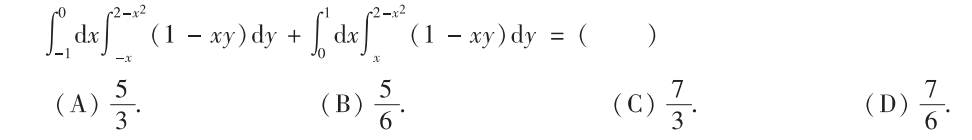
解析:画出积分区域后化简求值
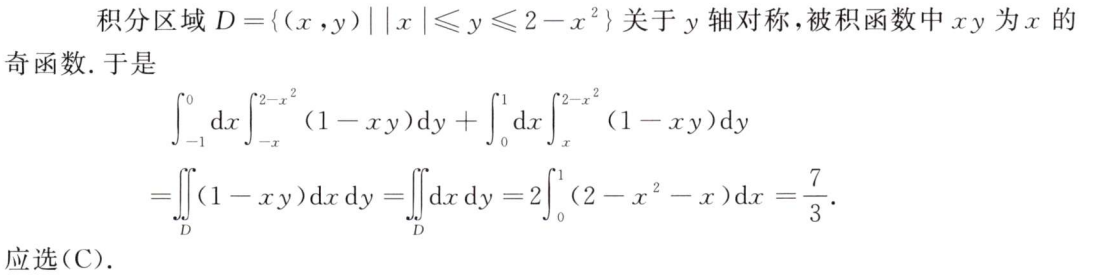
解析:可以用排除法,ABC都是对的,所以选D,也可以用比较法来判断
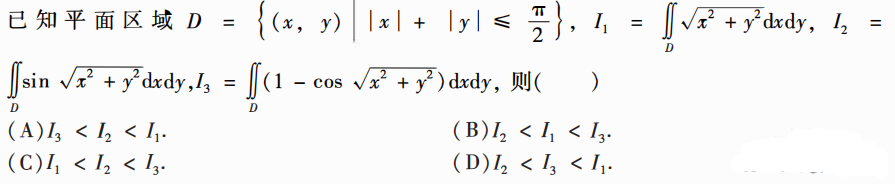
解析:积分区域一样,比较被积函数,都是偶函数,比较第一象限内函数即可,$x>sinx$,故1>2,而3可能为负数,所以1>2>3
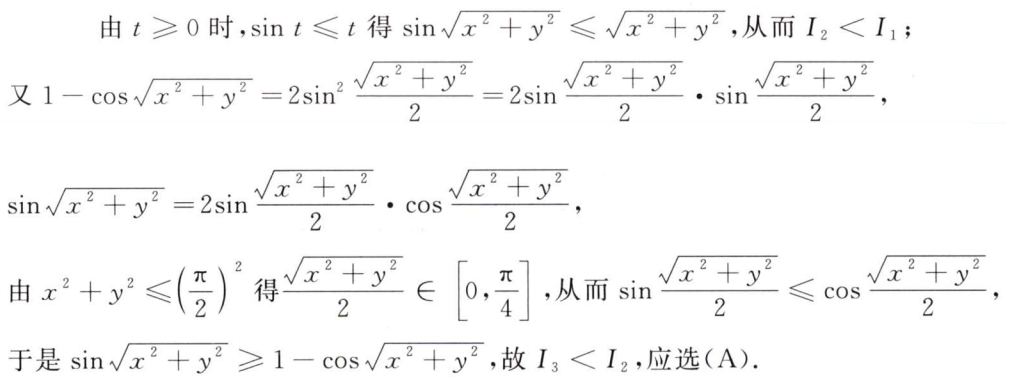
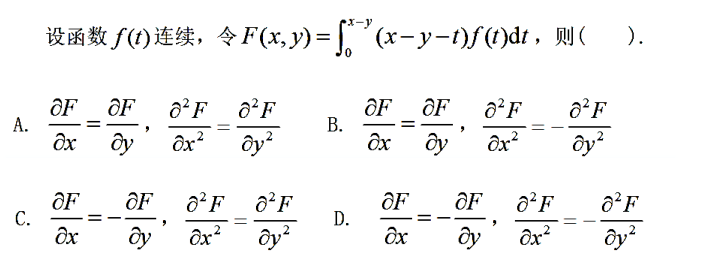
解析:拆分出来求导就是了
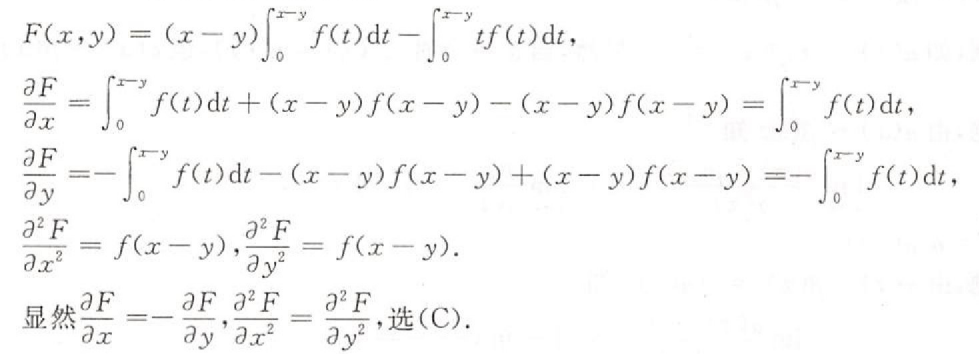
填
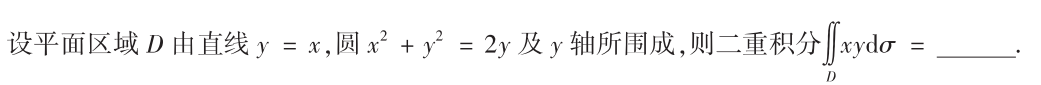
解析:画出积分区域后用极坐标代替运算:
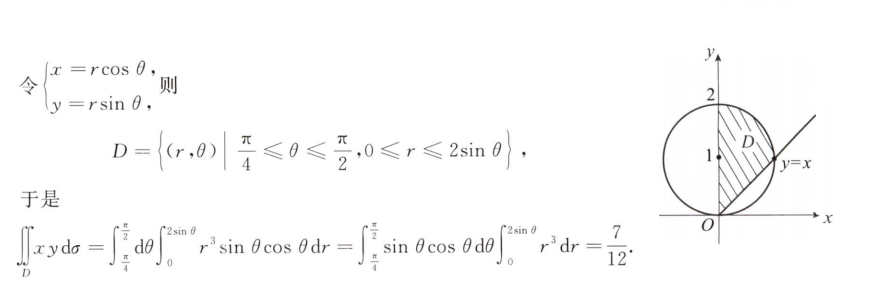
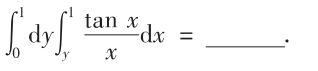
解析:交换积分顺序后求解
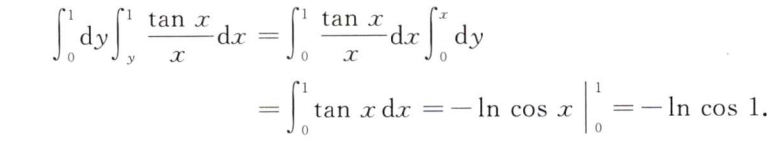
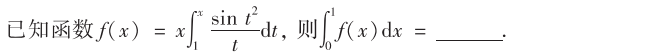
解析:经典的改变积分次序简化,但是要注意正负号!
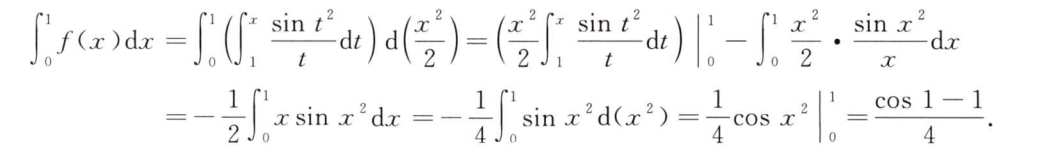
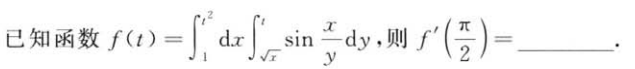
解析:改变次序后,再求导
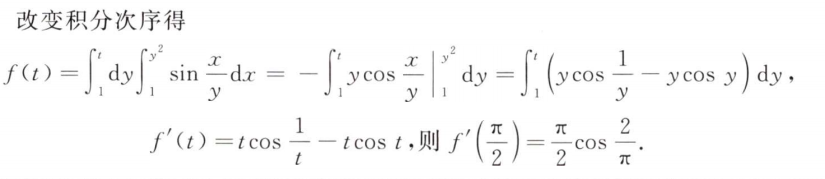
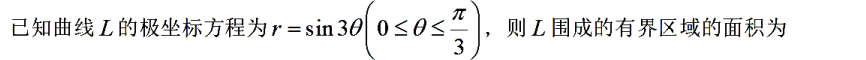
解析:
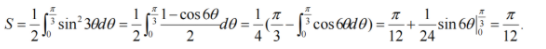
综

首先是需要解一个微分方程,其中题目暗含两个条件:$y(x)$过(0,0)和D的面积为2,可以完整的求出$y(x)$,然后按旋转体体积公式进行计算
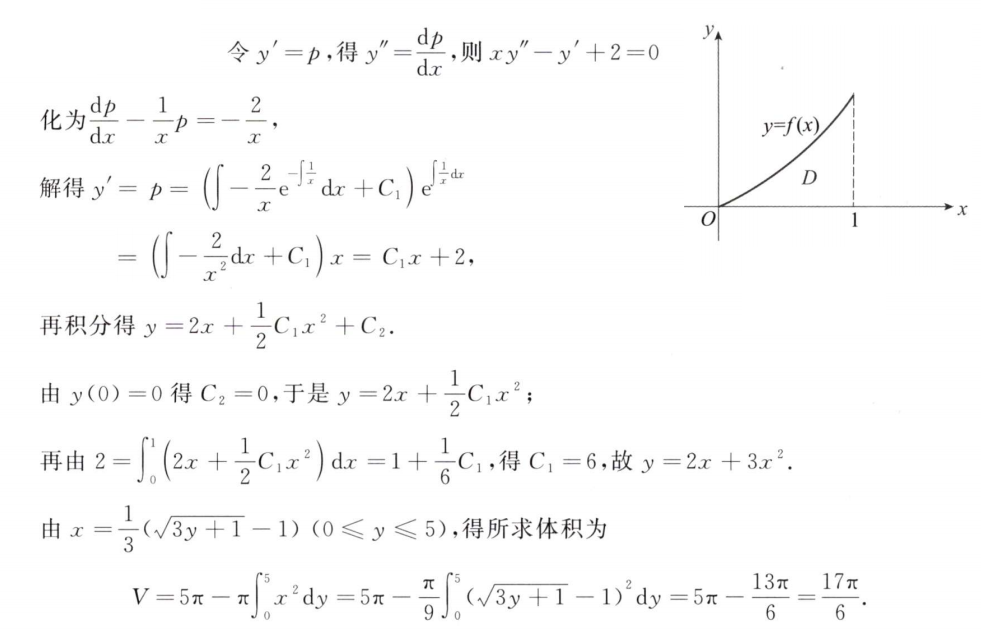
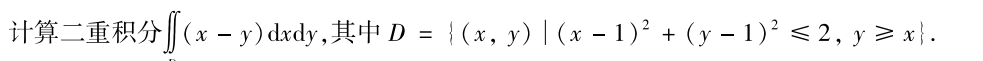
解析:此题是标准的平移题,只要将$x-1=u,y-1=v$,即可极大程度简化运算

解析:本题是考察极坐标转换为普通坐标,画出积分区域求解


解析:第一问就是求旋转体体积,按对称性计算较简单
第二问需要以截面为微元,即 $\pi x^2dy$,以$(2-y)$为距离进行积分
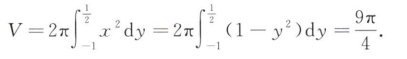
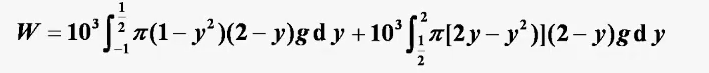
结果是$\frac{27}{8}\pi pg$

解析:多次应用换元法解出答案

解析:先求出切点,然后选面积和体积
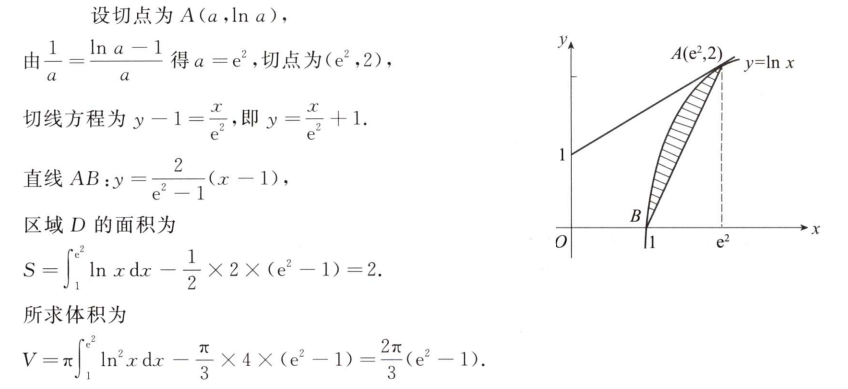
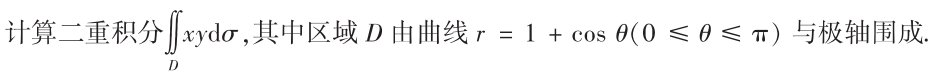
解析:主要是确定$r$和$\theta$的范围,以及$xy$与极坐标的转化
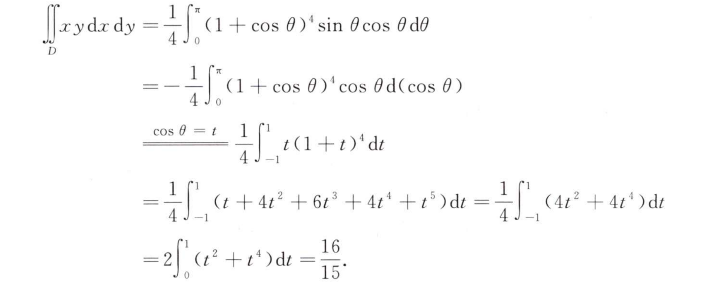
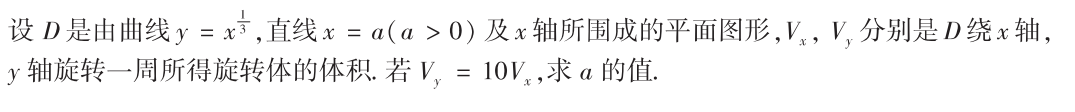
解析:常规计算题
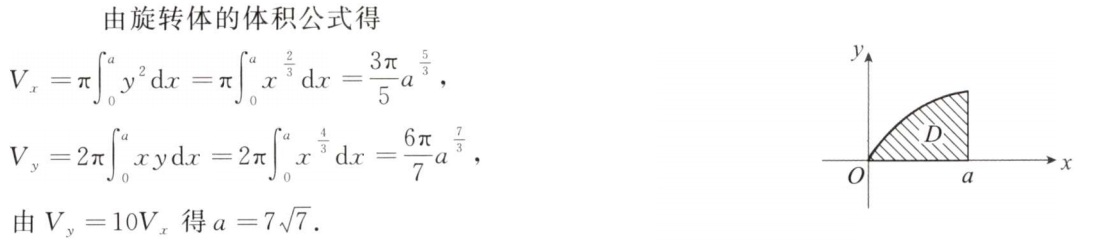
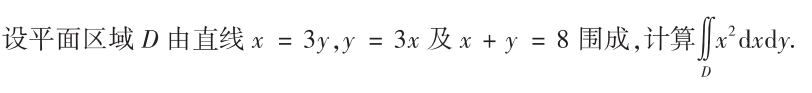
解析:画出积分区域,分成两块计算即可
解析:常规计算,注意形心公式

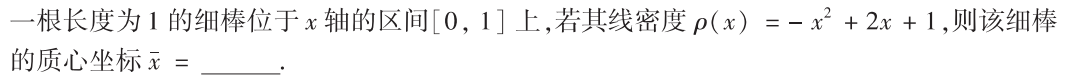
解析:算形心坐标:
解析:由对称性简化后求解

解析:主要是写出具体的公式,$2\pi\int_1^2dx\int_{-1}^{f(x)}(y+1)dy$

解析:常规题

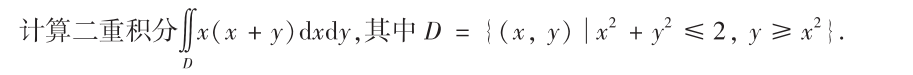
解析:首先对称性简化,然后用常规方法解题

解析:本题的特殊之处在于,用常规方程和极坐标方程都可以

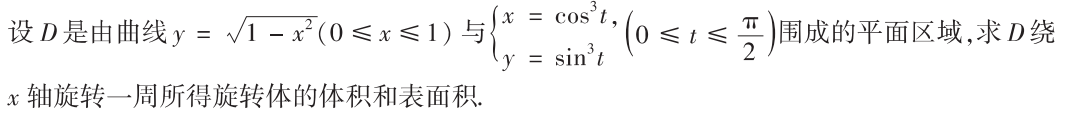
解析:要分别算出体积和表面积,体积是$V_1-V_2$,而表面积是$S_1+S_2$
对于参数方程来说,直接把公式中的$x,y$替换成参数计算即可


解析:第一问需要二重积分交换次序,第二问需要用单调性


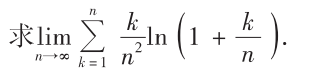
解析:利用定积分的定义化成定积分,再用分部积分法求解
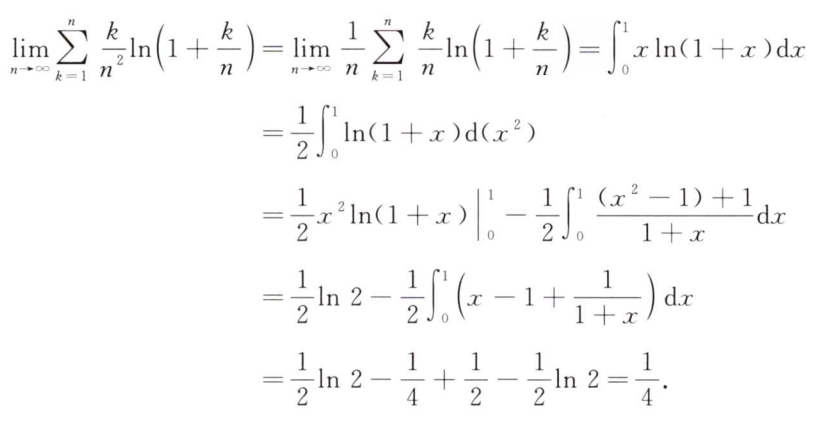
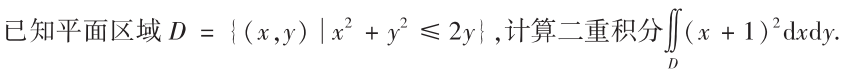
解析:常规题,注意点火公式的应用

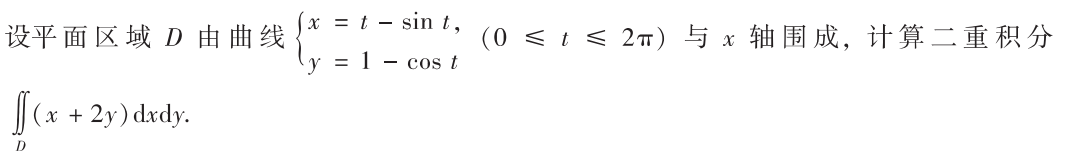
解析:和参数方程一样,根本不需要知道$g(x)$的具体表示,在$dx=x’dt$的时候,$g(x)$也换元成了$g(t)$
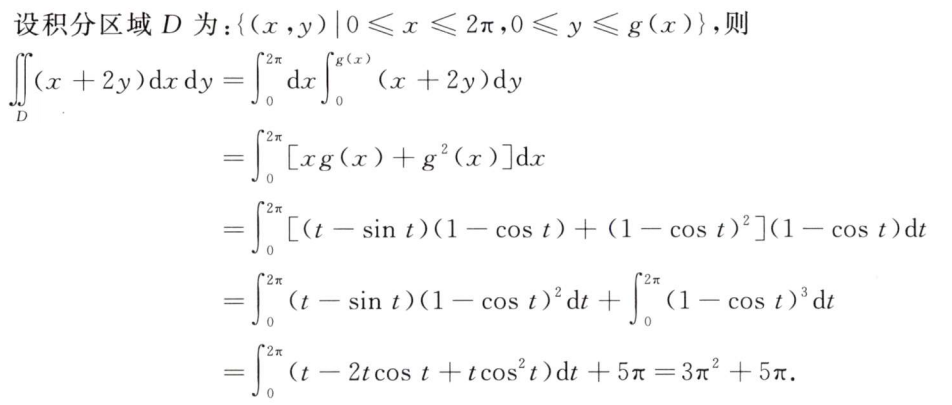
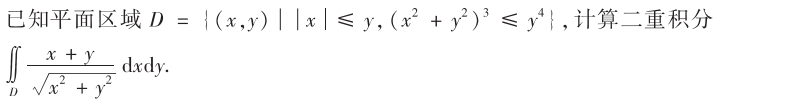
解析:本质上是算$sin\theta$的高次幂
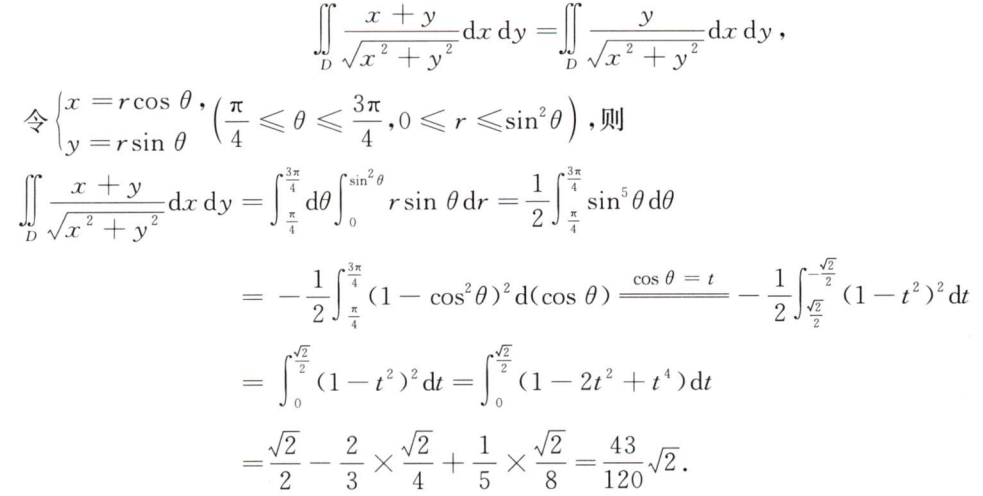
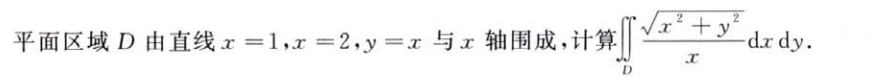
解析:前几年求$sin\theta$的高次幂,这次求$sec\theta$的高次幂了,实际上可以将$sec^3\theta dx$ 看做$secx dtan\theta$,即$\sqrt{1+tan^2x}dtanx$,$\int\sqrt{1+x^2}dx$可以由分部积分法计算出
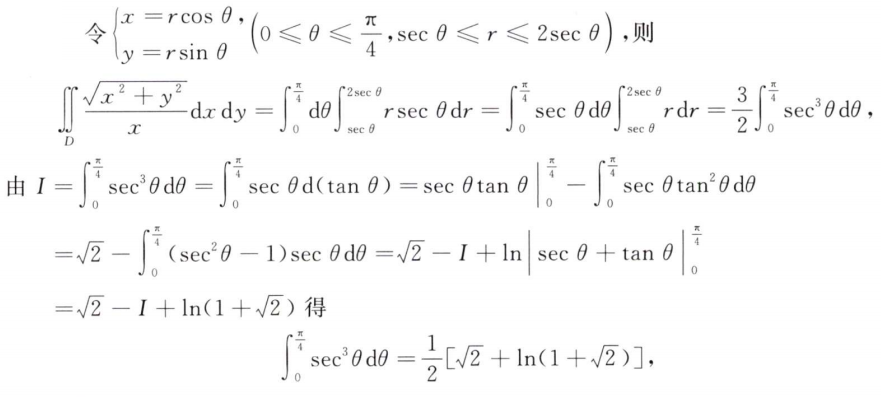
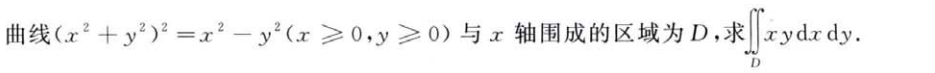
解析:注意$\theta$的变化范围要和$\rho$一致,所以并不是题目上的$0\sim\frac{\pi}{2}$,而是让$cos2\theta>0$,所以是$0\sim \frac{\pi}{4}$
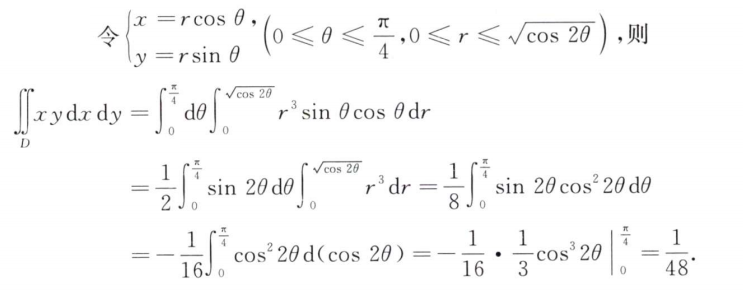
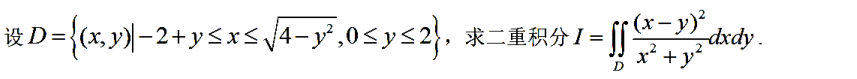

线性代数
选

解析:首先求出分块矩阵的行列式的值,然后根据$A^A=|A|E$,求出$A^$
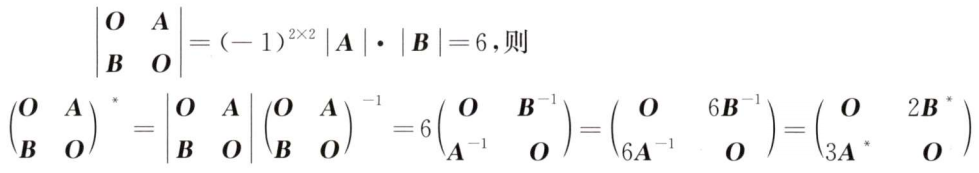
选B

解析:首先将$Q^T$和$Q$用$P^T$和$P$和另外一个初等矩阵之积表达出来,然后进行运算
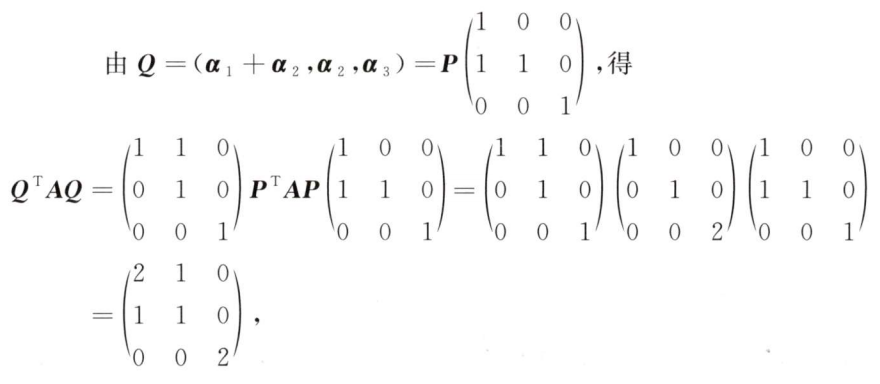
选A

解析:

解析:A的秩为3,那么必有一个特征值为0,然后要符合$\lambda^2+\lambda=O$,$\lambda=-1$符合这个条件,所以选D

解析:实际上是$P_2(AP_1)=E$,所以$A=P_2^{-1}P_1^{-1}$,而$P_2^{-1}=P_2$,所以选D

解析:首先判断出$r(A)=3$,则$r(A^)=1$,所以有三个基础解系,$AA^=O$,故$A$是一组解,而$A$中的$a_1$和$a_3$线性相关,故选D
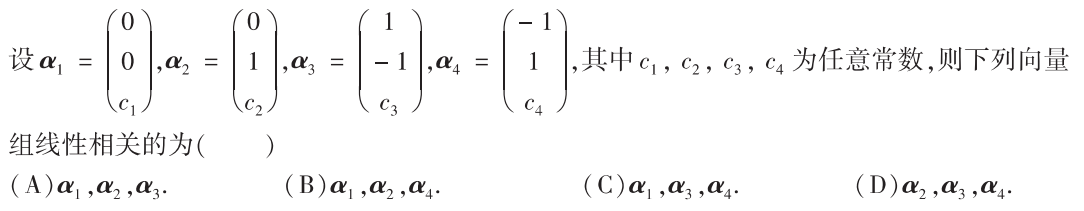
解析:$a_3+a_4$,可以直接得到$a_1$,所以选C

解析:先写出PQ关系,再带入换算,选B

解析:$B$可逆,相当于$A$经过初等列变化变为了$C$,所以选B

解析:
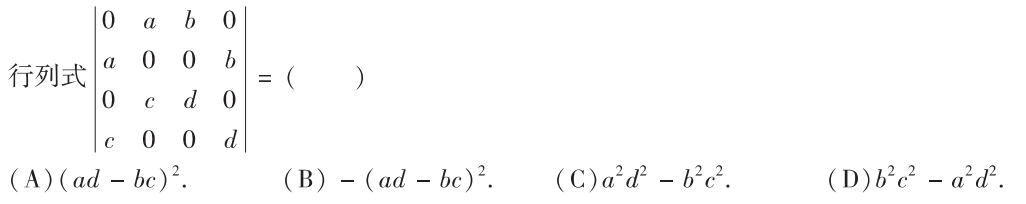
解析:选一行直接展开即可
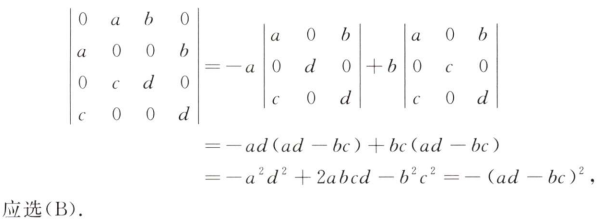

解析:直接代入特殊值,$k,l=0$时,可知是必要非充分条件,选A

解析:首先$|A|=0$,其次$r(A)=r(B)$


解析:和$P$对应即可,选A


解析:将选项带入$P^{-1}XP$中,C明显不符合

解析:可以直接算出特征值,也可以取$a=0$看是否符合条件,选C

解析:可以看出特征值就0,1,2,并且对应,所以选B
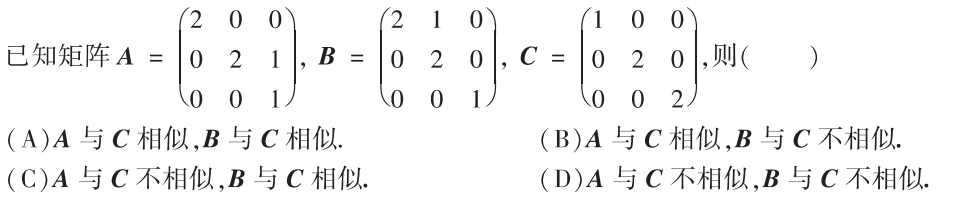
解析:特征值一样的情况下,看特征值对应的矩阵的秩,明显$AC$相似,和$B$不与$C$相似,选$B$

解析:首先可以看出特征值和行列式的值都一致,所以直接看特征值对应的矩阵的秩是否一致


解析:$(A,B)$的写法意思是:把$AB$矩阵拼在一起,所以对$A$进行初等列变化不会改变分块矩阵的秩,选A

解析:如果$A$的秩为2,那么$A^*$的秩为0

解析:根据方程算出两个特征值,根据行列式算出最后一个特征值,写出规范性
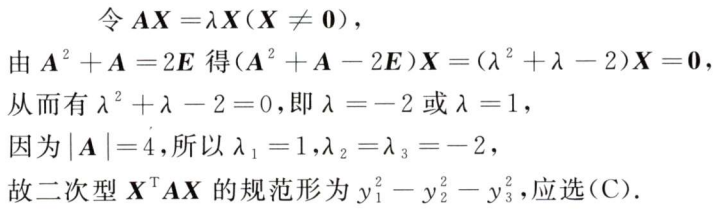

解析:$A_{12}≠0$,说明$A$的秩为3,$A^{*}$的秩为1,而且$A_{12}≠0$还表示第1,3,4列线性不相关,所以选C

解析:$AX=\lambda X$,所以选D
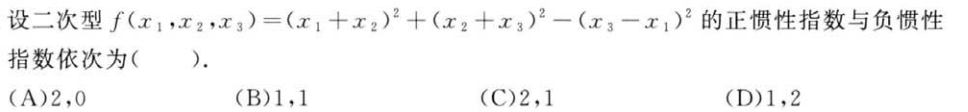
解析:全部算出来,然后看特征值
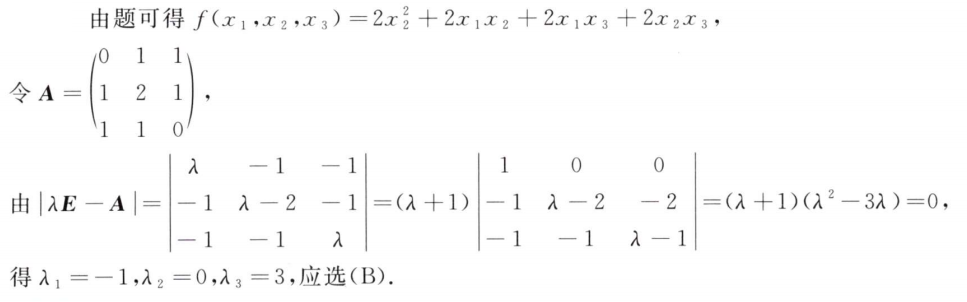

解析:$r(B)≥r(A)$


解析:全部带进去算
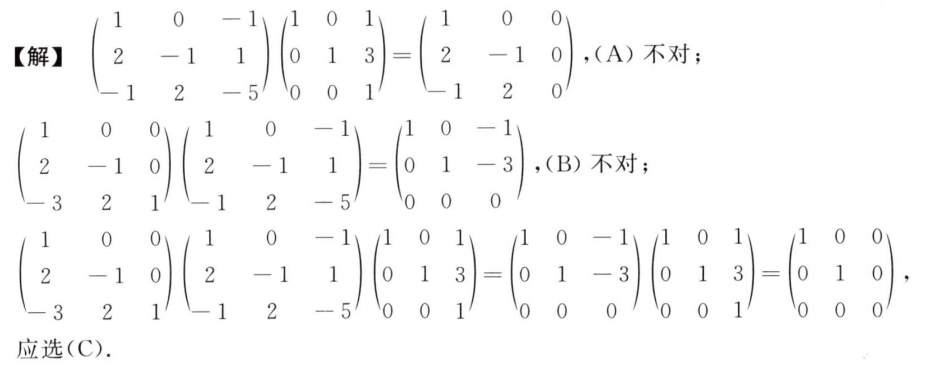

解析:按照可逆矩阵的定义,选B

解析:写出增广矩阵

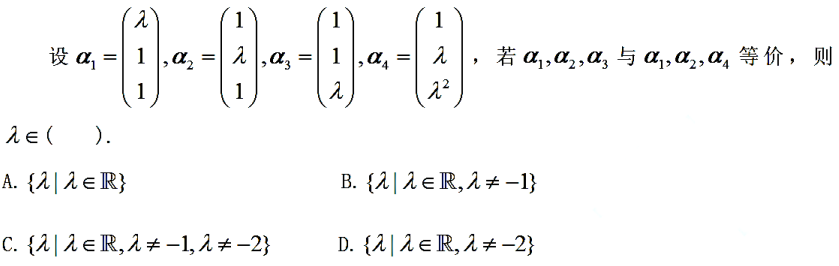
解析:写出这个两个矩阵,等价说明秩相同
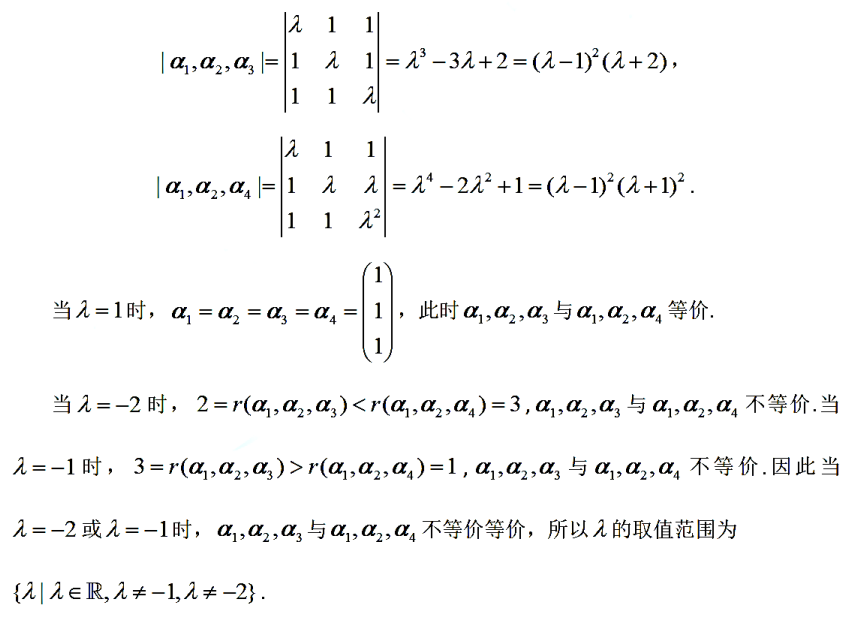
填

解析:根据秩为1的矩阵性质:
可以快速算出其值为2
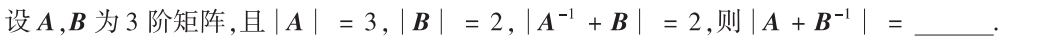
解析:原式拆成$|B^{-1}(A^{-1}+B)A|$,可以得到值为$\frac{1}{2}×2×3=3$
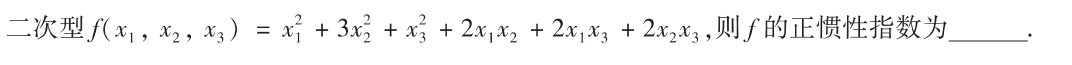
解析:求出特征值即可


解析:$|B|=-|A|$,而$|A^*|$的值也好求
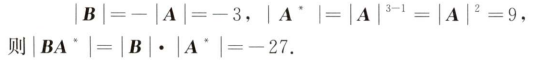

解析:最主要的是,$A^{T}=-A^{*}$

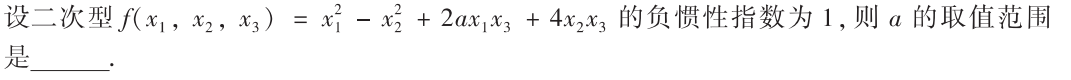
解析:负惯性系数为1$\implies$其行列式的值$≤0$

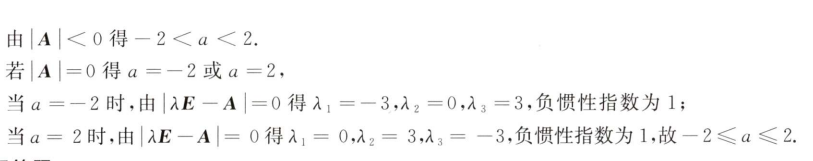
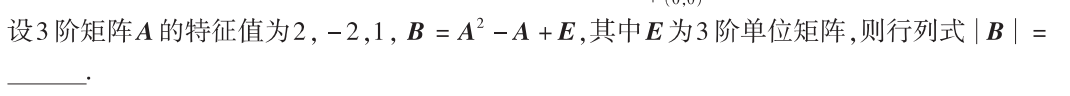
解析:把特征值带入方程即可
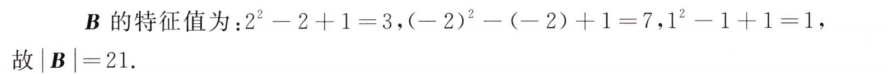
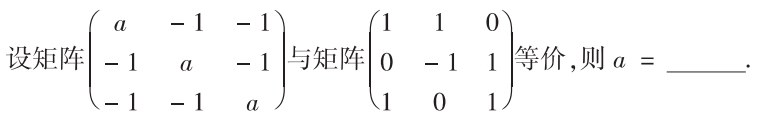
解析:秩要相同,算出a的可能取值,再排除一个
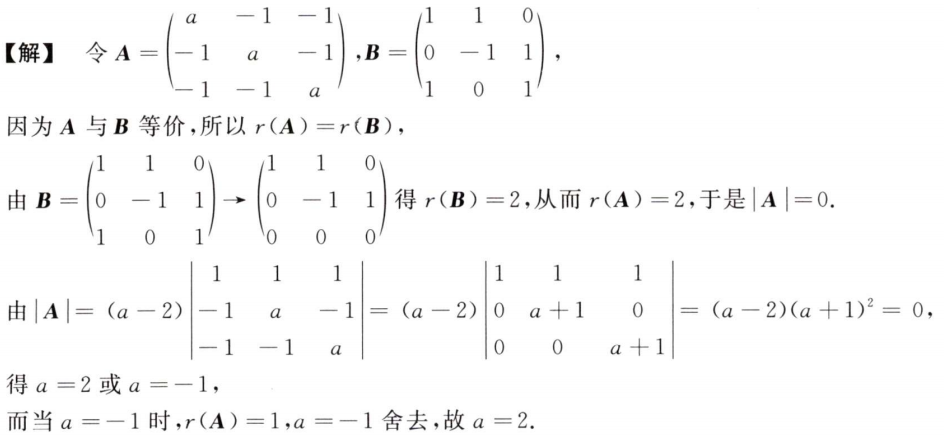

解析:$AX=\lambda X$,算出$a$的值


解析:写出矩阵,计算特征值即可


解析:单纯计算题
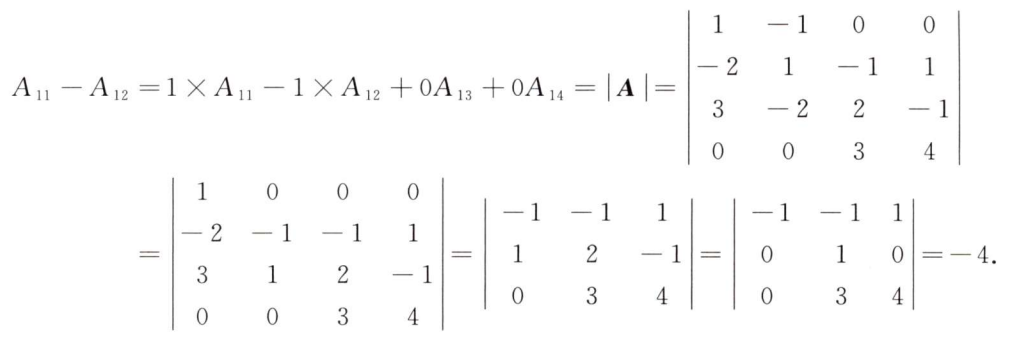
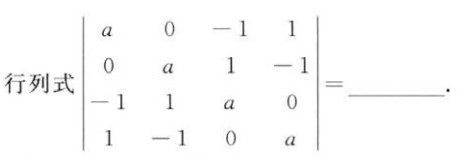
解析:化简之后计算即可

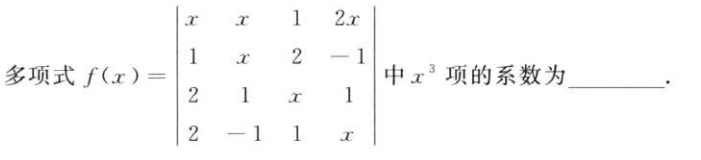
解析:利用逆序数解题
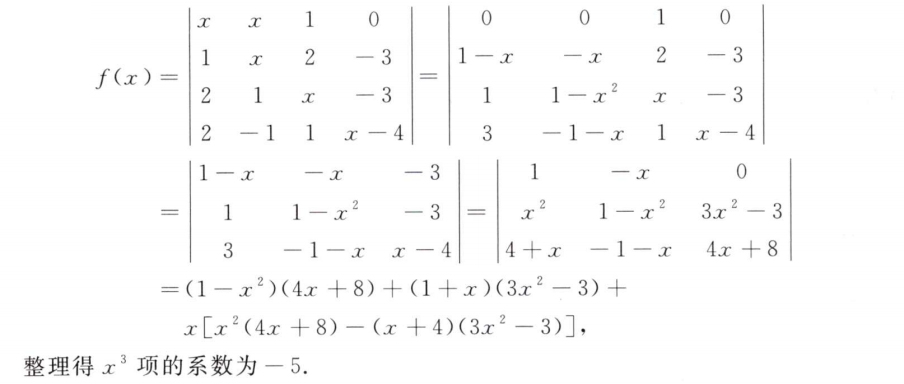

解析:只要算出$A$矩阵的迹,就可以知道$A^{-1}$的迹

综

解析:第1问是单纯的基础解系问题,至于第2问,需要列出通式,利用$A\xi_1=0$这个条件化简从而得出结论



只要求出了特征值以后,保证两个特征值>0,剩下一个特征值为0即可求出$a$的值
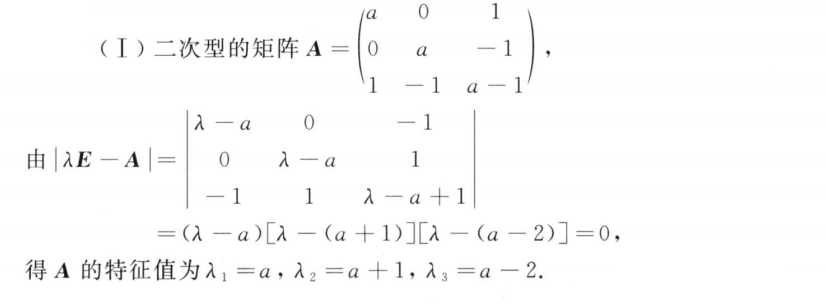


解析:存在多个解肯定不满秩,所以可以求出$\lambda$和$a$的值


解析:根据$AX=\lambda X$求解出$a$,然后算出其他特征值,求解出基础解系,正交化后写出$Q$



解析:$\beta_1,\beta_2,\beta_3$组成的矩阵的行列式的值肯定为0,可以直接算出$a$
然后按求解方程组的办法表示$\beta_1,\beta_2,\beta_3$,因为$a_1,a_2,a_3$是满秩矩阵,所以化简得到矩阵的列向量即是答案


解析:特征值很好求,特征向量可以根据正交矩阵的特质求出
重点是第二问,需要按相似矩阵的方式,$P^{-1}AP=\Lambda$,这样求出矩阵$A$


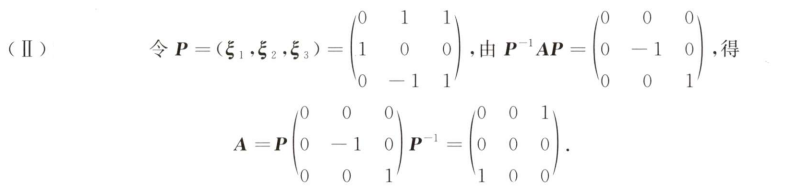

解析:有无穷多解的前提是行列式为0,根据$a$的值的可能性,化简矩阵,得到正确答案


解析:$A^T$和$A$的秩是一样的,所以可以求出$A$的值,然后对$AA^T$矩阵求特征值,正交化特征向量即可



解析:先把C矩阵假设出来,再带入列出方程,按照方程组有解的情况算出a,b,再解基础解系即可
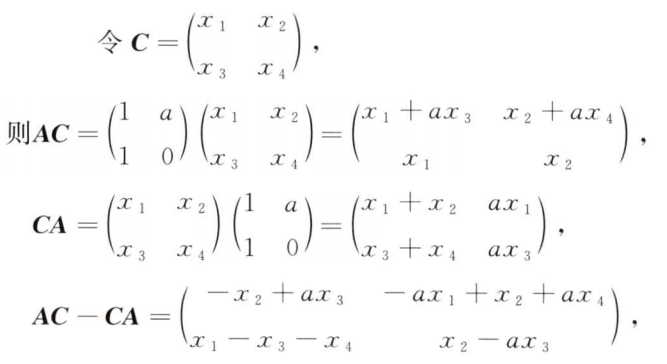


根据二次型的定义解决第1问,根据特征向量的定义解出第2问
解析:


解析:注意给最后一行添0后计算,针对第二个问,假设B为3个列向量,相当于解3个基础解系,可以一起算

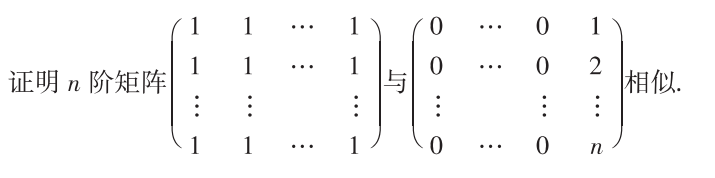
解析:求出第1个矩阵的特征值即可,要把每列的值加在第一列,提出来可化简,发现特征值和第2个矩阵一样
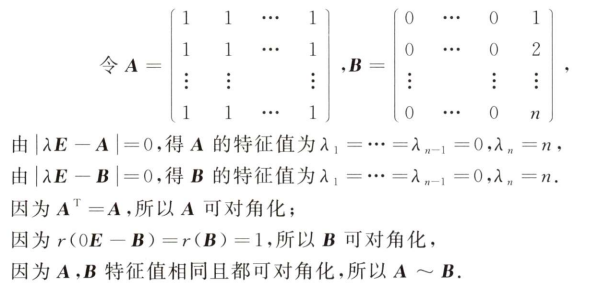
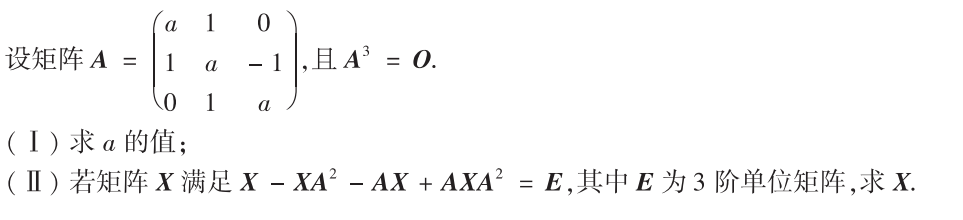
解析:$|A|=0$,算出a,然后化简方程就可以求出$X$

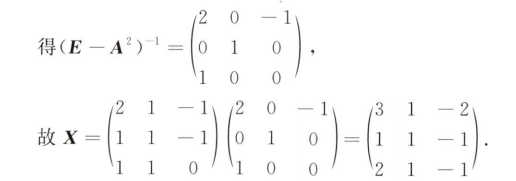

解析:根据迹相等和行列式值相等就可以算出来$a,b$的值了,之后算A的对角矩阵属于常规题


解析:无解说明$r(B)>r(A)$,算出A的值


解析:求A的高次幂,需要用相似矩阵求$P^{-1}A^{99}P=\Lambda^{99}$,所以求出$P$和$\Lambda$即可
$B^{100}=BA^{99}$



解析:因为$a_3$能被其他表示出来,所以$r<3$,因为3个不同的特征值,所以$r>1$,是2
第2问相当于在求基础解系,显然$(1,1,1)$是特解,找到通解即可

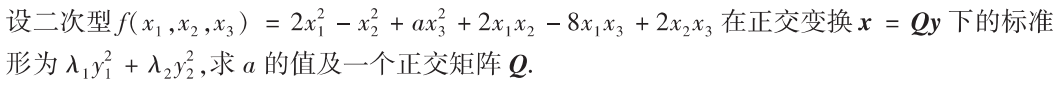
解析:标准形只有2个系数说明有一个特征值为0,所以矩阵的行列式为0求出$a$,然后就是常规方法求正交矩阵

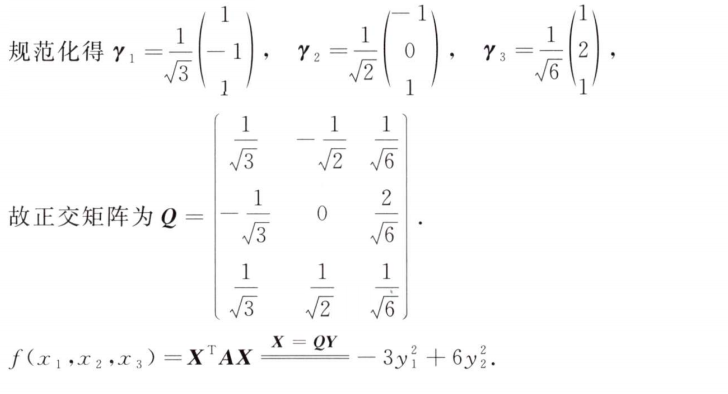
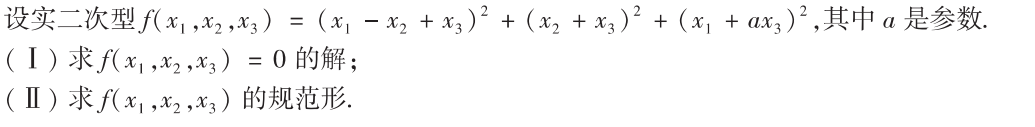
解析:得用配方法表示括号里面的数,构造一个矩阵,说明矩阵内行列式为0
而第2问是重点,因为拉格朗日配方法是只有用于可逆矩阵中,所以必须$a≠2$时才能用,其表示的规范形就如题所示,本质上就是做了坐标变化,而当$a=2$时就不能用配方法,而是求特征值的方式,来算特征值

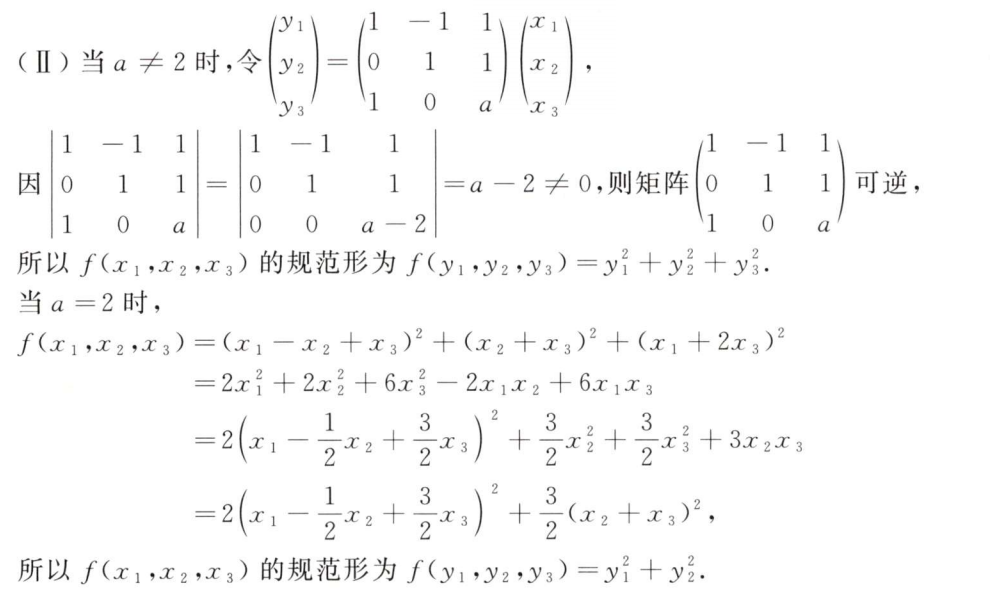

解析:$AB$的秩肯定是一样的,所以可算出$a$,然后根据基础解系的方法,$AX=B$,相当于算三个基础解系,组合成一个矩阵,即是$P$


解析:等价也就是秩相等,算出$a$的可能取值,再带入验证,之后就是常规的解基础解系
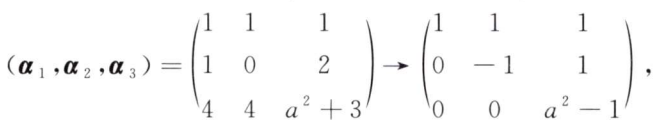


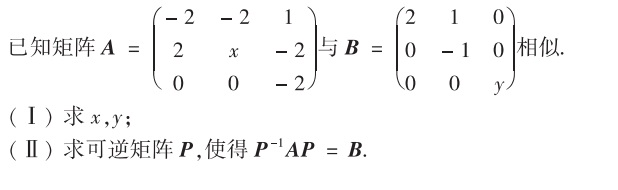
解析:第1问好求,而求解第2问,需要用等式$P^{-1}AP=Q^{-1}BQ$,则$(PQ^{-1})^{-1}A(PQ^{-1})=B$,最终但是$PQ^{-1}$



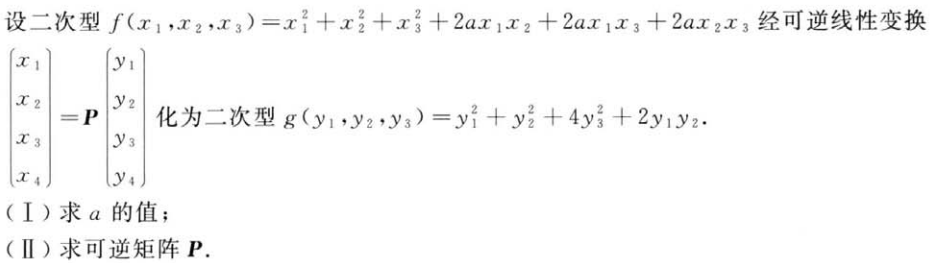
解析:$y$和$x$有相同的秩,可以求出$a$
根据$A^TXA=B^TYB$,$(AB^{-1})^{T}XAB^{-1}=Y$
但是因为两个矩阵的特征值不一样,只能用配方法求规范性

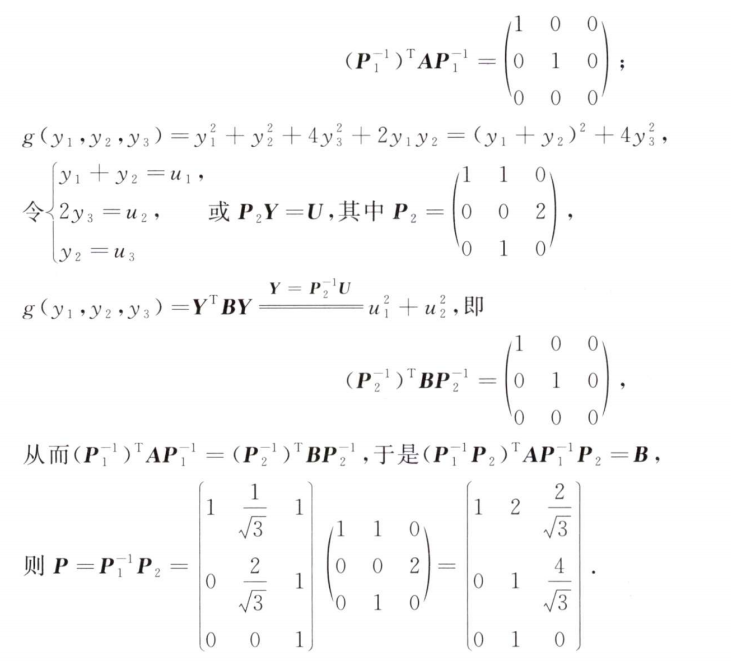

解析:第1问易证


解析:仅仅有2个不同的特征值,说明其特征值方程有重根,列出特征值方程,发现有2种情况,分类讨论即可


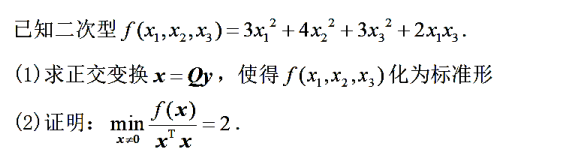
解析:常规解正交矩阵,而f(x)的最大值和最小值,取决于系数的最大最小值