一元函数微分学

导数与微分

概念

微分

定义

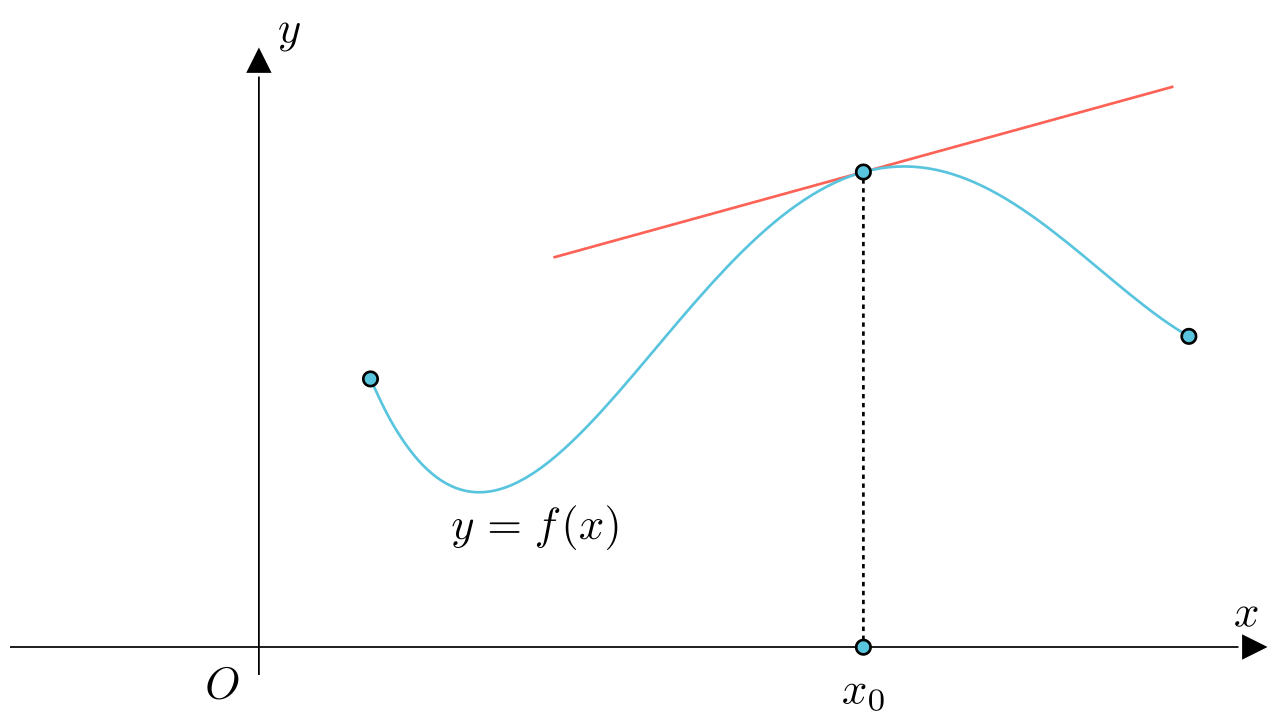
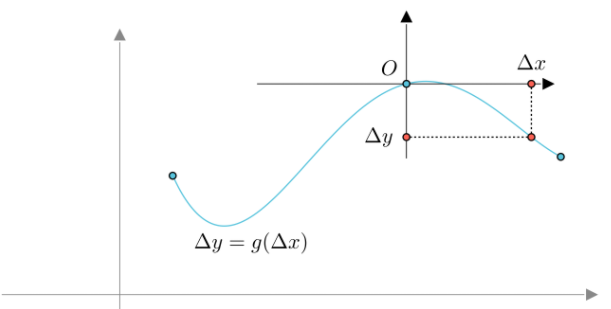
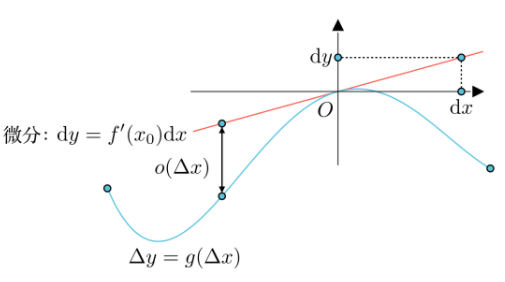
设函数$y=f(x$)在某区间内有定义，$x_0$及$x_0+\Delta x$在此区间内，如果函数增量：

$\Delta y=f(x_0+\Delta x)-f(x_0)$

可表示为：

$\Delta y=A\Delta x+o(\Delta x)$

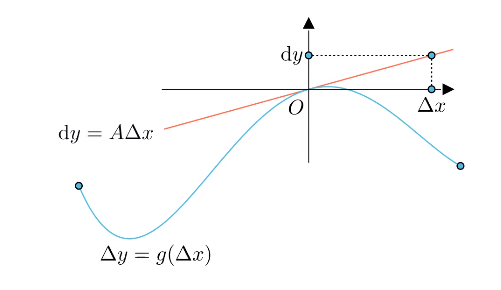
其中$A$是不依赖于$\Delta x$的常数，那么称函数$y=f(x)$在点$x_0$是可微的，而$A\Delta x$叫作函数$y=f(x)$在点$x_0$相应于自变量增量$\Delta x$的微分，记作$\textrm{d}y$，即：

$\textrm{d}y=A\Delta x$

通常令$\mathrm{d}x=\Delta x$，所以微分又可表示为$\textrm{d}y=A\mathrm{d}x$

微分就是对某段函数曲线的线性近似

推导过程

对于过$f(x_0)$点的某直线：

如果同样以曲线上的$f(x_0$)点为原点来建立新的坐标系，在该新坐标系中，上述直线的自变量为$\Delta x$，因变量让我们用$\mathrm{d}y$来表示：

因为在新坐标系中上述直线过原点，根据以前的高中知识，其函数可以写作$\mathrm{d}y=A\Delta x$，其中$A$为该直线的斜率：

微分定义中说如果有$\Delta y=A\Delta x+o(\Delta x)$，改写下就是如果有$\Delta y-A\Delta x=o(\Delta x)$，根据上面的分析，其实说的就是如果曲线和直线相差高阶无穷小$o(\Delta x)$：

那么该直线就是$f(x_0)$点及其附近曲线的“线性近似”，其函数$\mathrm{d}y=A\Delta x$就是函数$y=f(x)$在点$x_0$的微分。通常会令$\mathrm{d}x=\Delta x$，所以微分又可以表示为$\textrm{d}y=A\mathrm{d}x$：

这样就通过微分实现了函数的线性近似

导数

定义

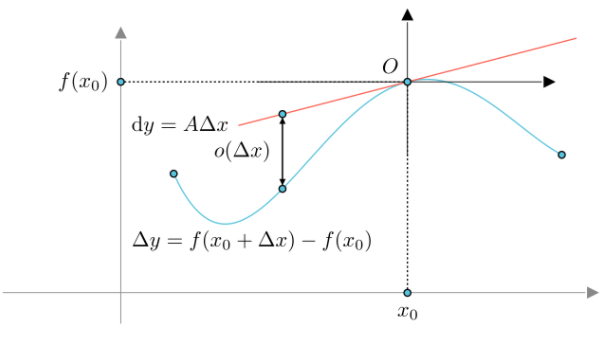
微分的表达式为$\textrm{d}y=A\mathrm{d}x$，那么$A$的具体计算过程如下：

根据微分的定义可知，有：

$\Delta y=A\Delta x+o(\Delta x)$

其中$o(\Delta x)$是$x\to x_0$时$\Delta x$的高阶无穷小，所以可推出：

$\begin{aligned} \Delta y=A\Delta x+o(\Delta x) &\implies \frac{\Delta y}{\Delta x}=A+\frac{o(\Delta x)}{\Delta x}\\ &\implies \lim_{x\to x_0}\frac{\Delta y}{\Delta x}=\lim_{x\to x_0}\left(A+\frac{o(\Delta x)}{\Delta x}\right)\\ &\implies \lim_{x\to x_0}\frac{\Delta y}{\Delta x}=\lim_{x\to x_0}A+\lim_{x\to x_0}\frac{o(\Delta x)}{\Delta x}=A\\ \end{aligned}$

因为$\Delta x=x-x_0$，所以$x\to x_0$就是$\Delta x\to 0$；又因为$\Delta y=f(x_0+\Delta x)-f(x_0)$，所以上式可改写如下，也就是推出了$A$的计算式：

$\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=A$

即为导数的定义式

严格定义：

设函数$y=f(x)$在点$x_0$的某个邻域内有定义，当自变量$x$在$x_0$处取得增量$\Delta x$（点$x_0+\Delta x$仍在该邻域内）时，相应的，因变量取得增量$\Delta y=f(x_0+\Delta x)-f(x_0)$。如果$\Delta y$与$\Delta x$之比在$\Delta x\to 0$时的极限存在，那么称函数$y=f(x)$在点$x_0$处可导，并称这个极限为函数$y=f(x)$在点$x_0$处的导数，记为$f’(x_0)$，即：

$f'(x_0)=\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

也可记作$y’|_{x=x_0}，\left.\frac{\mathrm{d}y}{\mathrm{d}x}\right|_{x=x_0}，\left.\frac{\mathrm{d}f(x)}{\mathrm{d}x}\right|_{x=x_0}$或$\left.\frac{\mathrm{d}}{\mathrm{d}x}f(x)\right|_{x=x_0}$

为了方便书写也常令$\Delta x=h$，将上述定义式改写为：

$f'(x_0)=\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}$

或者令$x=x_0+\Delta x$，相应的上述定义式改写为：

$f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}$

从上面的几何意义可知，导数其实就是微分的斜率，因此如果微分存在，那么必然导数存在，反之亦然。所以说，可微即可导，可导即可微。

切线方程：$y-f(x_0)=f’(x_0)(x-x_0)$

法线方程：$y-f(x_0)=-\frac{1}{f’(x_0)}(x-x_0)$

左导数与右导数

定义：

如下极限存在的话，则称之为函数$y=f(x)$在点$x_0$处的左导数，记作$f’_-(x_0)$：

$f'_-(x_0)=\lim_{\Delta x\to 0^-}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

或如下极限存在的话，则称之为函数$y=f(x)$在点$x_0$处的右导数，记作$f’_+(x_0)$：

$f'_+(x_0)=\lim_{\Delta x\to 0^+}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

如果函数在某点左导数和右导数存在，说明在左右两边都连续，则在该点连续

可导的充要条件：左、右导数存在且相等

所以$\Delta x$要能从左右两边都趋向于$0$，例如

$\lim_{h\to0}\frac{f(1-cosh)-f(0)}{1-cosh}$

这种形式就不能判定在$x=0$处可导，因为$cosh$在零点附近恒为正，所以$1-cosh≥0$，只能说明其右导数存在，不能说明左导数存在

同时$\Delta x≠0$

连续与可导

定理：如果函数$y=f(x)$在$x_0$点可导，则可推出该函数$y=f(x)$在$x_0$点连续

而连续$\nRightarrow$可导，因为即使在$x_0$处连续，其左右导数仍有可能不相等

连续且可导的函数，导函数一定是存在的，但导函数不一定连续，因为也可能含有振荡间断点

设$f(x)$在$x=a$可导，关于$|f(x)|$在$x=a$是否可导有以下结论：

若$f(a)≠0$，则$|f(x)|$在$x=a$可导

若$f(a)=0$，则需要判定其导数$f’(a)$，若$f’(a)=0$，则$|f(x)|$在$x=a$可导，若$f’(a)≠0$，则不可导

如果是$\phi(x)|f(x)|$的形式，如果$f’(a)≠0$，但$\phi(a)=0$，最终结果是$0$，则还是可导的

如果反过来说，已知$|f(x)|$在$a$点可导，同时$f(x)$在$a$点连续，那么可以推出，$f(x)$在$x_0$处可导

可导+可导=可导

可导+不可导=不可导

不可导+不可导=不确定

导函数

定义

若函数$y=f(x)$在开区间$I$内的每点处都可导，则称函数$y=f(x)$在开区间$I$内可导

此时对于任意$x\in I$，都对应着$f(x)$的一个确定的导数值，这就构成了新的函数，该函数叫作$y=f(x)$的导函数，记作$y’$、$f’(x)$、$\frac{\textrm{d}y}{\textrm{d}x}$或$\frac{\textrm{d}f(x)}{\textrm{d}x}$，定义式为：

$y'=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\quad\text{或}\quad f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

基本初等函数的求导公式

$\begin{array}{c|c|c} \hline \\ \quad常数函数\quad &\quad f(x)=C,C\in\mathbb{R} & f'(x)=0\\ \\ \hline \\ \quad幂函数\quad &\quad f(x)=x^\alpha,\alpha\in\mathbb{R} & f'(x)=\alpha x^{\alpha-1}\\ \\ \hline \\ \quad\quad &\quad f(x)=\sin x & f'(x)=\cos x\\ \quad三角函数\quad &\quad f(x)=\cos x & f'(x)=-\sin x\\ \quad\quad &\quad f(x)=\tan x & f'(x)=\sec^2 x\\ \quad\quad &\quad f(x)=\cot x & f'(x)=-\csc^2 x\\ \\ \hline \\ \quad\quad &\quad f(x)=\arcsin x & f'(x)=\frac{1}{\sqrt{1-x^2}}\\ \quad反三角函数\quad &\quad f(x)=\arccos x & f'(x)=-\frac{1}{\sqrt{1-x^2}}\\ \quad\quad &\quad f(x)=\arctan x & f'(x)=\frac{1}{1+x^2}\\ \quad\quad &\quad f(x)=\text{arccot} x & f'(x)=-\frac{1}{1+x^2}\\ \\ \hline \\ \quad\quad &\quad f(x)=a^x,a > 0, a\ne 1& f'(x)=a^x\ln a\\ \quad指数函数\quad &\quad f(x)=e^x & f'(x)=e^x\\ \\ \hline \\ \quad\quad &\quad f(x)=\log_a x,a > 0, a\ne 1& f'(x)=\frac{1}{x\ln a}\\ \quad对数函数\quad &\quad f(x)=\ln x & f'(x)=\frac{1}{x}\\ \\ \hline \end{array}$ $(\sec x)'=\sec x\tan x \qquad (\csc x)'=-\csc x\cot x \qquad (\cot x)'=-csc^2 x\qquad$

有理运算法则

$\begin{aligned} \left[u(x)\pm v(x)\right]'=u'(x)\pm v'(x)\\\\ \left[u(x)v(x)\right]'=u'(x)v(x)+u(x)v'(x)\\\\ \left[\frac{u(x)}{v(x)}\right]'=\frac{u'(x)v(x)-u(x)v'(x)}{v^2(x)} \end{aligned}$

复合函数求导

定理（链式法则）：如果$u=g(x)$在$x$点可导，而$y=f(u)$在$u=g(x)$点可导，那么复合函数$y=f[g(x)]$在$x$点可导，其导数为：

$\frac{\textrm{d}y}{\textrm{d}x}=f'(u)g'(x)\quad\text{或}\quad\frac{\textrm{d}y}{dx}=\frac{\textrm{d}y}{\textrm{d}u}\cdot\frac{\textrm{d}u}{\textrm{d}x}$

如果链式法则能用，即$f’(u)$和$g’(x)$都存在,那么这个方法最简单
如果某一个函数导数不存在，也不能说明整个函数的导数不存在，需要将$g(x)$带入到$f(x)$中，形成完整的函数再判断

隐函数求导法则

$F(x,y)=0\qquad\frac{dy}{dx}=-\frac{F_x}{F_y}$

求某点的隐函数时，先根据方程该该点的$y，x$都求出来在带进去，如果是二阶导，那把$y’(x_0)$也求出来

反函数求导

定理 .如果函数$x=f(y)$在区间$I_y$内严格单调、可导且$f’(y)\neq 0$，那么它的反函数$y=f^{-1}(x)$在区间$I_x=\{x|x=f(y), y\in I_y\}$内也可导。且：

$[f^{-1}(x)]'=\frac{1}{f'(y)}\quad\text{或}\quad\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{\frac{\mathrm{d}x}{\mathrm{d}y}}$

二阶导数有

$\frac{d}{dx}(\frac{dx}{dy})\frac{dx}{dy}=-\frac{f''(x)}{[f'(x)]^2}·\frac{1}{f'(x)}$

题目会给出$y$的值，需要先换算成$x$，在带入方程中

参数方程求导

对于参数方程$\begin{cases}x=\varphi(t)\\y=\psi(t)\end{cases}$，如果：

存在严格单调且连续的反函数$t=\varphi^{-1}(x)$
存在函数$y=\psi(t)=\psi(\varphi^{-1}(x))$ ，$x=\varphi(t)$以及$y=\psi(t)$可导，且$\varphi’(t)\ne 0$
则

$\frac{\textrm{d}y}{\textrm{d}x}=\frac{\psi'(t)}{\varphi'(t)}$

二阶导数：

$\frac{\textrm{d}y^2}{\textrm{d}x^2}=\frac{d}{dt}(\frac{\psi'(t)}{\varphi'(t)})·\frac{1}{\varphi'(t)}$

也就是

$\frac{y''(0)x'(0)-x''(0)y'(0)}{x'^3(0)}$

对数求导法

适用于幂指函数$y=x^x$，$y=x^{sinx}$，以及多因子乘幂函数$\sqrt{x^2·sinx·(1-x^2)}$

通过对等式两边取对数，然后再同时对$x$求导，计算关于$y’$的方程

高阶导数

常见的高阶导数：

$\begin{aligned} (\sin x)^{(n)}=\sin(x+n\cdot\frac{\pi}{2}) \\(\cos x)^{(n)}=\cos(x+n\cdot\frac{\pi}{2}) \\(uv)^{(n)}=\sum_{k=0}^n{n\choose k}u^{(n-k)}v^{(k)} \end{aligned}$

分段函数

求形如

$f(x)=\left\{ \begin{aligned} \quad g(x)&,x≠x_0\\A&,x=x_0 \end{aligned} \right.$

分段函数在分段点的导数一般要用定义来求，或函数在分段点连续的条件下求导数的极限，即用下面定理求分段函数在分段点的导数：

$f(x)$在$x_0$处连续
$f(x)$在$x_0$的某空心邻域内可导
$\lim_{x\to x_0}f’(x)$存在，则$f’(x)=lim_{x\to x_0}f’(x)$

在连续的情况下：$lim_{x \to x_0}f’(x)$才有意义

微分中值定理

费马引理

设函数$f(x)$在点$x_0$的某邻域$U(x_0)$内有定义，且在$x_0$点可导，如果对任意的$x\in U(x_0)$，有：

$f(x)\le f(x_0)\qquad（\text{或}\ f(x)\ge f(x_0）$

即在$x_0$处取得极值，那么$f’(x_0)=0$

实际上可以简化为：

$\left. \begin{aligned} f(x_0)\ 为极值点\\ x=x_0\ 点可导 \end{aligned} \right\} \implies f'(x_0)=0$

罗尔定理

如果函数$y=f(x)$满足：

在闭区间$[a,b]$上连续
在开区间$(a,b)$上可导
$f(a)=f(b)$

那么$\exists\xi\in(a,b)$，使得$f’(\xi)=0$

罗尔定理的推论：若在区间$I$上$f^{n}(x)≠0$，则方程$f(x)=0$在$I$上最多$n$个实根

求方程的根的个数时，最常用的方法就是

单调性
罗尔定理推论

罗尔定理的推论可以推出最多有多少个根，单调性可以判断至少有多少个根

在面对$x=kf(x)$类题目，求根的个数时，推荐将$k=\frac{x}{f(x)}$的形式，分离参数出来，根据分析$\frac{x}{f(x)}$的函数图像，可以通过k的取值来判断根的个数

注意题目中如果给出：$f’’(x)<0$或$>0$的情况，可以用泰勒公式：

$f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f^{(2)}(\xi)}{(2)!}(x-x_0)^{2}$

由于$(x-x_0)^2$是肯定$>0$的，所以根据题目给出的二阶导的正负来判断$f(x),f’(x)$的正负，从而就可以判断整体的正负

关于罗尔定理和单调性的联系，以下给出一些结论及证明

如果$f(x)$在$[0,+\infty)$上有二阶导数，$f(0)=0,f_+’(0)<0,f''(x)≥M>0(x>0)$，$f(x)=0$在$(0,+\infty)$内有唯一实根

显然$f_+’(0)<0$说明在0的右邻域里面有$f(x_1)<0$，由拉格朗日中值定理

$f’(x)=f’(0)+f’’(\xi_1)(x-0)≥f’(0)+Mx\to +\infty(x\to +\infty)$

其中$\xi$介于$0$与$x$之间，故存在充分大的$x_0 \in(0,+\infty)$，使得在$(x_0,+\infty)$内有$f’(x)>1$

对$f(x)$用拉格朗日中值定理

$f(x)=f(x_0)+f’(\xi_2)(x-0)≥f(x_0)+(x-x_0)\to +\infty(x\to +\infty)$

其中$\xi_2$介于$x_0$与$x$之间，于是存在充分大的$x_2\in (x_0,+\infty)$，使得$f(x_2)>0$,所以在$(0,+\infty)$至多有一个根

再根据罗尔定理的推论，$f’’(x)>0$，故至多有$2$个根，所以在$(0,+\infty)$内有唯一实根
设$f(x)$在区间$[a,b]$上有二阶导数，且$f(a)=f(b)=0,f_+’(a)f’_-(b)>0$，在$(a,b)$存在两点$\xi,\eta$，使得$f(\xi)=0,f’’(\eta)=0$

证明：图像上容易看出来，证明$f(\xi)=0$，可以用反证法，假设不存在$f(\xi)=0$,
$f’_+(a)=\lim_{x \to a^+}\frac{f(x)-f(a)}{x-a}=\lim_{x \to a^+}\frac{f(x)}{x-a}≥0$ $f’_-(b)=\lim_{x \to b^-}\frac{f(x)-f(b)}{x-b}=\lim_{x \to b^+}\frac{f(x)}{x-b}≤0$
这样$f’_+(a)f’_-(b)≤0$,与题目矛盾，故必有解

$f(a)=f(\xi)=f(b)$，在$[a,\xi]$与$[\xi,b]$上对$f(x)$分别用罗尔定理，可以找出两点$f’(\eta_1),f’(\eta_2)=0$,在$[\eta_1,\eta_2]$上再用罗尔定理，即可证明$f’’(\eta)=0$

拉格朗日中值定理

如果函数$y=f(x)$满足：

在闭区间$[a,b]$上连续
在开区间$(a,b)$上可导

那么$\exists\xi\in (a,b)$，使得

$f'(\xi)=\frac{f(b)-f(a)}{b-a}$

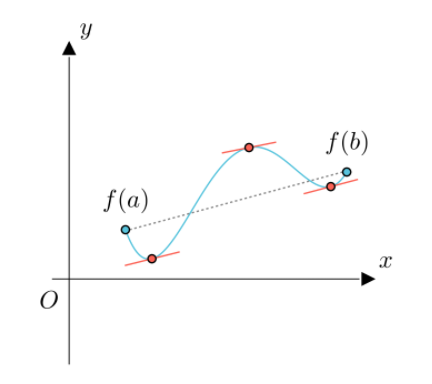
拉格朗日中值定理的意思是，$f(a)$、$f(b)$之间存在某点（甚至不止一点），其微分与$f(a)$、$f(b)$的连线平行

$\xi$ 为$(a,b)$中某点，也可以等价表述为$f’(a+\theta (b-a))$ $\theta\in{0,1}$

证明过程

引进辅助函数：

$F(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a)$

容易知道，$F(x)$满足：

在闭区间$[a,b]$上连续
在开区间$(a,b)$上可导
$F(a)=F(b)=0$

所以根据罗尔中值定理可知，$\exists\xi\in(a,b)$使得$F’(\xi)=0$，即：

$F'(x)|_{x=\xi}=\left.f'(x)-\frac{f(b)-f(a)}{b-a}\right|_{x=\xi}=f'(\xi)-\frac{f(b)-f(a)}{b-a}=0$

由此可得$f’(\xi)=\frac{f(b)-f(a)}{b-a}$。

柯西中值定理

如果函数$f(x)$及$g(x)$满足

在闭区间$[a,b]$上连续
在开区间$(a,b)$上可导
$\forall x\in(a,b)$有$g’(x)\neq 0$

那么$\exists\xi\in (a,b)$，使得

$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(\xi)}{g'(\xi)}$

证明过程

证明所需结论。构造辅助函数：

$F(x)=f(x)-\frac{f(b)-f(a)}{g(b)-g(a)}g(x)$

容易知道，$F(x)$满足：

在闭区间$[a,b]$上连续
在开区间$(a,b)$上可导
$F(a)=F(b)=\frac{g(b)f(a)-g(a)f(b)}{g(b)-g(a)}$

所以根据罗尔中值定理，$\exists\xi\in(a,b)$使得$F’(\xi)=0$，即：

$F'(x)|_{x=\xi}=\left.f'(x)-\frac{f(b)-f(a)}{g(b)-g(a)}g'(x)\right|_{x=\xi}=f'(\xi)-\frac{f(b)-f(a)}{g(b)-g(a)}g'(\xi)=0$

由此可得$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f’(\xi)}{g’(\xi)}$

几何理解

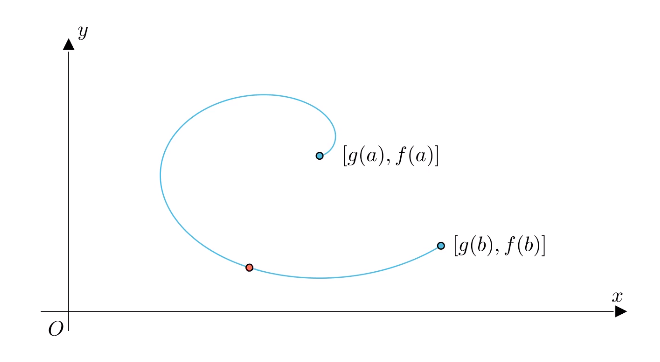
假设有参数方程：

$\begin{cases}x=g(x)\\y=f(t)\end{cases}$

上述参数方程描述的是某种运动轨迹，如下图所示。根据该参数方程可知，$a$时刻所在的位置为$[g(a), f(a)]$点，$b$时刻所在的位置为$[g(b), f(b)]$点：

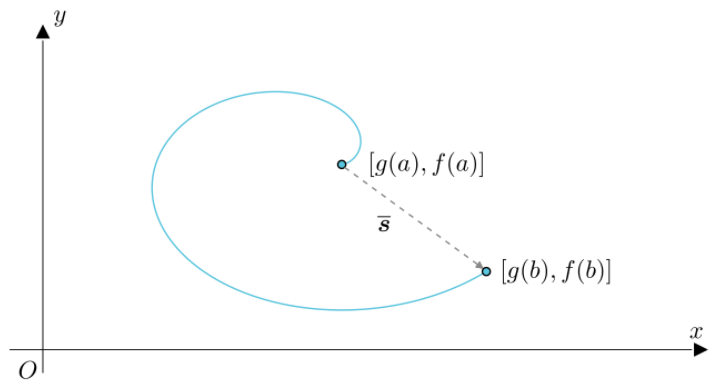
$[g(a), f(a)]$点到$[g(b), f(b)]$点的向量$\overline{\boldsymbol{s}}$指明了最终的运动方向：

根据常识可知，需要不断调整运动的方向，才能从$[g(a), f(a)]$点运动到$[g(b), f(b)]$点。也就是说，瞬时速度向量$\boldsymbol{v}$必然会在某个时刻与$\overline{\boldsymbol{s}}$平行：

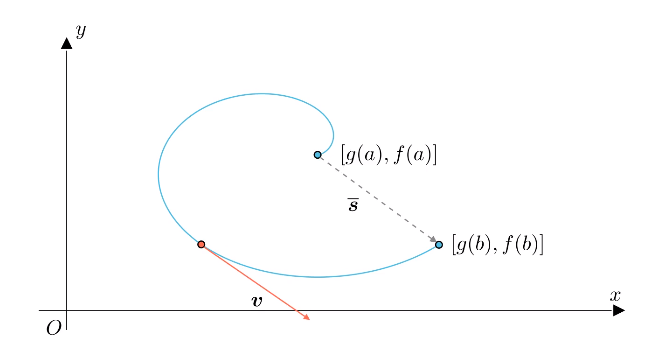
容易知道，向量$\overline{\boldsymbol{s}}$的斜率为$\frac{f(b)-f(a)}{g(b)-g(a)}$；而之前计算过瞬时速度向量$\boldsymbol{v}$的斜率为$\frac{f’(t)}{g’(t)}$。假设在$\xi\in(a,b)$时刻两者平行，那么就有：

$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(\xi)}{g'(\xi)}$

泰勒定理

牛顿插值法

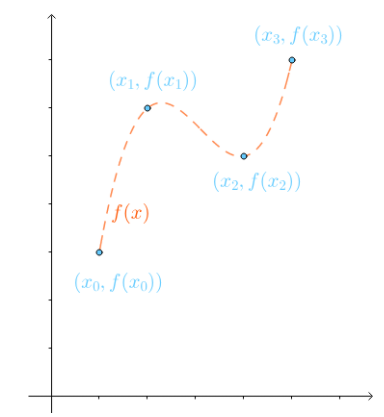
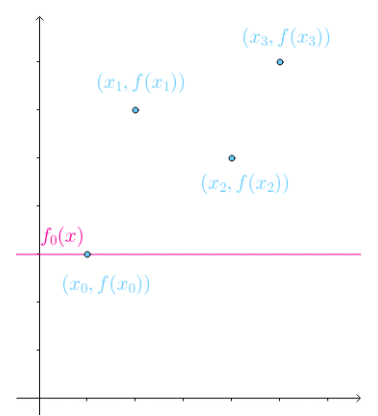
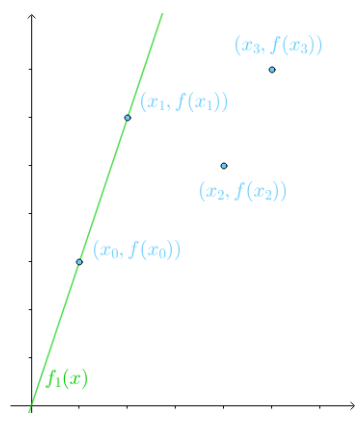
知道某几个点的坐标，要求预测其他点的位置，这就是牛顿插值法需要解决的问题

在牛顿插值法里，是通过已知的点坐标，建立一个多项式，用来拟合曲线，则曲线上的点就是其他点的位置

多项式即：

$f_n(x)=f[x_0]+f[x_0,x_1](x-x_0)+\cdots+f[x_0,x_1,\ldots,x_n]\prod_{k=0}^{n-1}(x-x_k)$

证明过程

假设已知的就是这4个点，需要通过牛顿插值法求该曲线的方程

首先，拿出第一个点$(x_0,f(x_0))$，可以构造一个函数：

$f_0(x)=f(x_0)$

如果没有更多的信息，可以认为$f_0(x)=f(x)$，因为它符合所有已知的信息：

$f_0(x_0)=f(x_0)$

其函数图像如下：

曲线$f_0(x)$为过第一个点的拟合曲线函数

当然，这里还有第二个点$(x_1,f(x_1))$。为了把第二个点包含进来，我们在$f_0(x)$基础上增加一部分构造新的拟合曲线函数：

$f_1(x)=f_0(x)\color{red}{+b_1(x-x_0)}$

该方程显然会穿过$(x_0，f(x_0))$，接下来需要计算$b_1$

$f_1(x)$穿过第二个点$(x_1,f(x_1))$，因此可以推出：

$f_1(x_1)=f(x_0)+b_1(x_1-x_0)=f(x_1)\implies b_1=\frac{f(x_1)-f(x_0)}{x_1-x_0}$

综上可得：

$f_1(x)=f(x_0)+\frac{f(x_1)-f(x_0)}{x_1-x_0}(x-x_0)$

新的拟合曲线如下：

为了把第三个点$(x_2,f(x_2))$也包含进来，我们再在$f_1(x)$的基础上增加一部分构造新的函数：

$f_2(x)=f_1(x){+b_2(x-x_0)(x-x_1)}$

根据新增的信息求出$b_2$：

$b_2=\frac{\frac{f(x_2)-f(x_1)}{x_2-x_1}-\frac{f(x_1)-f(x_0)}{x_1-x_0}}{x_2-x_0}$

加上刚才得到的$f_1(x)$，可知：

$\begin{aligned} f_2(x)= &f(x_0)+\frac{f(x_1)-f(x_0)}{x_1-x_0}(x-x_0)+\frac{\frac{f(x_2)-f(x_1)}{x_2-x_1}-\frac{f(x_1)-f(x_0)}{x_1-x_0}}{x_2-x_0}(x-x_0)(x-x_1) \end{aligned}$

可以验证，$f_2(x)$函数满足我们已知的三个点：

$f_2(x_0)=f(x_0),\quad f_2(x_1)=f(x_1),\quad f_2(x_2)=f(x_2)$

可以推论出，如果要知道第$n$个点的信息，牛顿插值法的公式为：

$f_n(x)=f[x_0]+f[x_0,x_1](x-x_0)+\cdots+f[x_0,x_1,\ldots,x_n]\prod_{k=0}^{n-1}(x-x_k)$

泰勒公式

假设插值点之间是等距的：

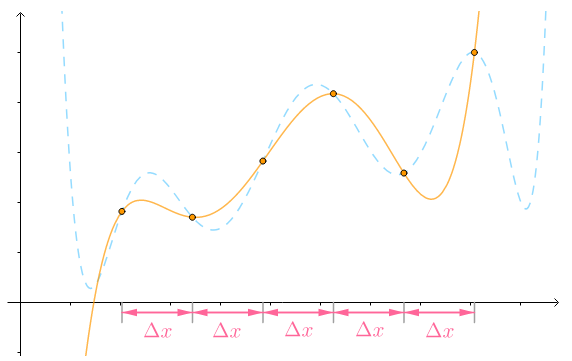
那么根据牛顿插值法：

$\begin{aligned} f_5(x)=&f[x_0]+f[x_0,x_1](x-x_0)\\ &+f[x_0,x_1,x_2](x-x_0)(x-x_1)\\ &+f[x_0,x_1,x_2,x_3](x-x_0)(x-x_1)(x-x_2)\\ &+f[x_0,x_1,x_2,x_3,x_4](x-x_0)(x-x_1)(x-x_2)(x-x_3)\\ &+f[x_0,x_1,x_2,x_3,x_4,x_5](x-x_0)(x-x_1)(x-x_2)(x-x_3)(x-x_4) \end{aligned}$

其中：

$x_1=x_0+\Delta x,\quad x_2=x_0+2\Delta x,\quad\cdots,\quad x_5=x_0+5\Delta x$

泰勒发现，当$\Delta x\to 0$时，$f_5(x)$变成了：

$\begin{aligned} \lim_{\Delta x\to 0}f_5(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2 +\frac{f^{(3)}(x_0)}{3!}(x-x_0)^3+\frac{f^{(4)}(x_0)}{4!}(x-x_0)^4 +\frac{f^{(5)}(x_0)}{5!}(x-x_0)^5 \end{aligned}$

对比之前的牛顿插值法：

$f_1(x)=f(x_0)+\frac{f(x_1)-f(x_0)}{x_1-x_0}(x-x_0)$

将$x_1=x_0+\Delta x$,则表达式为

$f_1(x)=f(x_0)+\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}(x-x_0)$

即

$\lim_{\Delta x\to 0}f_2(x)=f(x_0)+f'(x_0)(x-x_0)$

而推广此结论，将所有的$x_n$都替换成$x_0+\Delta x$的形式，后面的$(x-x_n)$因为$\Delta x$ 可以忽略，则都是$x-x_0$的$n$次方，则可以得到泰勒公式：

$\begin{aligned} p_n(x)= &f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\cdots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \end{aligned}$

特别的，如果在$x=0$处生成的泰勒多项式，也称为$\color{Salmon}{n阶麦克劳林多项式}$：

$p_n(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\cdots+\frac{f^{(n)}(0)}{n!}x^n$

余项

假设$f(x)$在$x=x_0$处有$n$阶导数，则有：

$\overbrace{f(x)=\quad\underbrace{p_n(x)}_{泰勒多项式}\quad+\quad\underbrace{R_n(x)}_{\color{Salmon}{余项}}}^{\color{Salmon}{泰勒公式}}$

其中：

$R_n(x)=o\left((x-x_0)^n\right)$

称为$\color{Salmon}{皮亚诺余项}$。

假设$f(x)$在$U(x_0)$内具有$n+1$阶导数，则在$U(x_0)$存在$n$阶泰勒多项式$p_n(x)$，同样有泰勒公式：

$f(x)=p_n(x)+R_n(x)$

此时$R_n(x)$可以表示为：

$R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}$

其中，$\xi$为$x_0$及$x$之间的某个值。该余项称为$\color{Salmon}{拉格朗日余项}$

通常把皮亚诺余项当做局部的余项，在研究极值和极限的时候会用到

而拉格朗日余项是整体的余项，在研究最值和证明不等式的时候会用到，尤其是在要求证明$f(c)=x_0$，还有是$|f’(c)|$小于or大于某个具体的值

具体方法是利用泰勒公式，将$f(x)$在信息多的点展开，然后用拉格朗日余项表示出来，不同的点展开的拉格朗日余项中的$\xi$不同，然后根据题目条件(比如$f’’(x)<a$）,证明不等式

常见的泰勒展开

$e^{x}=1+x+\frac{x^{2}}{2 !}+\cdots+\frac{x^{n}}{n !}+o\left(x^{n}\right)$ $sin x=x-\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}-\cdots+(-1)^{n} \frac{x^{2 n+1}}{(2 n+1) !}+o\left(x^{2 n+2}\right)$ $cos x=1-\frac{x^{2}}{2 !}+\frac{x^{4}}{4 !}-\frac{x^{6}}{6 !}+\cdots+(-1)^{n} \frac{x^{2 n}}{(2 n) !}+o\left(x^{2 n}\right)$ $ln (1+x)=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\cdots+(-1)^{n-1} \frac{x^{n}}{n}+o\left(x^{n}\right)$ $\frac{1}{1-x}=1+x+x^{2}+\cdots+x^{n}+o\left(x^{n}\right)$ $(1+x)^{m}=1+m x+\frac{m(m-1)}{2 !} x^{2}+\cdots+\frac{m(m-1)\cdots\left( m-n+1 \right)}{n!} x^{n}+o\left(x^{n}\right)$

微分中值定理的证明题

类型一：证明$G[\xi,f’(\xi),f(\xi)]$的函数等于$0$

方法1：如果函数相对简单可以考虑直接用零点定理证明两端点值异号

特别是出现了唯一的情况下，一般是先构造函数，证明两端点值异号，再通过求函数的单调性，说明只有唯一的一个点

方法2：先推导出原函数$F’(x)=G(x)$，如果$F(x)$的两端点值相等的话，用罗尔定理，则证明有$F’(\xi)=G(\xi)=0$

最难的一步就是求出$G(x)$的原函数，通常用微分方程求解，解出微分方程，使其变为$F(x)=C$的形式，最终得到$F’(x)=0$的结果，则$F(x)$就是原函数

以下是常见的形式：

$\xi f’(\xi)+nf(\xi)=0\qquad F(x)=x^nf(x)$ $\xi f’(\xi)-nf(\xi)=0\qquad F(x)=\frac{f(x)}{x^n}$ $f'(\xi)+\lambda f(\xi)=0\qquad F(x)=e^{\lambda x}f(x)$ $\alpha f'(\xi)+\beta f(\xi)=0\qquad F(x)=e^{\frac{\alpha}{\beta} x}f(x)$ $f'(\xi)+g'(\xi)f(\xi)=0\qquad F(x)=e^{g(x)}f(x)$ $f'(\xi)+g(\xi)f(\xi)=0\qquad F(x)=e^{\int g(x)}f(x)$

主要都是通过微分方程求解

当然题目给出的方程并不总是符合以上标准型，所以需要通过构造

补充一个积分中常见的形式，要证明$\int_0^{\xi}f(x)dx=0$，可以将$F(x)$设置成如下形式：

$F(x)=\int_0^x(x-t)f(t)dt$

可以根据题目条件进行改变，比如$F(x)=\int_0^x(x^2-t^2)f(t)dt$,那么$F’(x)=2x\int_0^{x}f(x)dx$，如果$F(x)$在两端点处等于$0$，一样可以证明结论

如果题目给出

$\int_a^bf(x)dx=0$

那么可设

$F(x)=\int_a^xf(x)dx$

这样构造满足：$F(a)=F(b)=0$，可以说明$F’(x)=f(\xi)=0$

类型二：证明存在两个点$\xi，\eta \in(a,b)$，使$F[\xi,\eta,f(\xi),f(\eta),f’(\xi),f’(\eta)]=0$

方法：

如果不要求$\xi≠\eta$，那么在同一区间$[a,b]$上用两次中值定理(拉格朗日，柯西)，比如只出现了$f’(\xi)$，那么用拉格朗日就行了，如果出来了$\eta f’(\eta)$之类的形式，就需要用到柯西
如果要求$\xi≠\eta$，将区间$[a,b]$分为两个子区间，在两个子区间上分别用拉格朗日中值定理，那么重要的是确定中间的分界点，诀窍是先假定点$c$使等式成立，然后再确定该点函数

类型三：证明存在一个中值点$\xi \in (a,b)$，使$F[\xi,f^(n)(\xi)≥0(n≥2)]$

方法：

用带拉格朗日余项的泰勒公式，其中$x_0$点选题目中提供函数值和导数值信息多的点

结论：设$f(x)$在$[a,b]$连续，且$f(a)=f(b)$，证明：至少存在一点$\xi \in (a,b)$，使得$f(\xi)=f(\xi+\frac{b-a}{n})$($n$为任意实数)

证明如下：

假设$g(x)=f(x)-f(x+\frac{b-a}{n}) ,x\in [a,b-\frac{b+a}{n}]$

$g(a)+g(\frac{b-a}{n})+···g(b-\frac{b-a}{n})=f(b)-f(a)=0$

若$g(a)+g(\frac{b-a}{n})+···g(b-\frac{b-a}{n})=f(a)-f(b)=0$，即结论易证，0=0

若$g(a)+g(\frac{b-a}{n})+···g(b-\frac{b-a}{n})$不全为0，则其中必有正值和负值，由零点定理，存在一点$\xi \in(a,b)$使得$g(\xi)=0$,即$f(\xi)=f(\xi+\frac{b-a}{n})$

如果给定了$n$的数值，则只需要解出$g(a)+g(b-\frac{b-a}{n})=0$即可

如果要证明$f(x)=c$，可以先求$f’(x)=0$,说明$f(x)$恒为常数，然后代入某个好算的点求出常数$c$

导数的应用

极值

必要条件

若$f(x)$在$x_0$处可导，且在$x_0$处取得极值，则$f’(x_0)=0$

极值点可能是驻点，但是驻点不一定是极值点

$f(x_0)\ 是极值点\color{red}{\mathrel{\rlap{\hskip .5em/}}\Longleftarrow} f'(x_0)=0$

极值可能出现在：驻点，没有定义的点

第一充分条件(在$x_0$处导数变号)

设函数$f(x)$在$x_0$处连续，且在某去心邻域$\mathring{U}(x_0,\delta)$内可导(或$f(x)$在$x_0$处连续)，则：

若$x\in(x_0-\delta,x_0)$时，$f’(x) > 0$，而$x\in(x_0,x_0+\delta)$时，$f’(x) < 0$，则$f(x)$在$x_0$处取得极大值；
若$x\in(x_0-\delta,x_0)$时，$f’(x) < 0$，而$x\in(x_0,x_0+\delta)$时，$f’(x) > 0$，则$f(x)$在$x_0$处取得极小值；
若$\mathring{U}(x_0,\delta)$时，$f’(x)$的符号保持不变，则$f(x)$在$x_0$处没有极值。

第二充分条件(观察二阶导数)

设函数$f(x)$在点$x_0$处二阶可导且$f’(x_0)=0$，则：

$f’’(x_0) < 0$，$f(x_0)$为极大值；
$f’’(x_0) > 0$，$f(x_0)$为极小值。

证明过程

由于二阶导数存在，写出$x_0$处的二阶泰勒多项式：

$f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+o((x-x_0)^2)$

由于$f’(x_0)=0$，所以：

$f(x)-f(x_0)= \frac{f''(x_0)}{2!}(x-x_0)^2+o((x-x_0)^2)$

再根据$f’’(x_0) < 0$,则在$x_0$的某个充分小的邻域内：

$f(x)-f(x_0)\approx \frac{f''(x_0)}{2!}(x-x_0)^2 < 0$

所以$x_0$处为极大值。

第三充分条件(观察偶数阶导是否不等于0，是第二充分条件的推广)

设$f(x)$在$x_0$处$n(n≥2)$可导，且：

$f'(x_0)=f''(x_0)=···=f^{n-1}(x_0)\qquad f^n(x_0)≠0,$

当$n$为偶数时$f(x)$在$x_0$处取得极值，其中当$f^{n}(x_0)>0$时取得极小值，当$f^{n}<0$时取得最大值
当$n$为奇数时，$f(x)$在$x_0$处无极值

某区间上函数的最值只有三种情况：

驻点
不可导的点
端点值

只须考察$f(x)$在$x = x_0$处的连续性及$f(x)$在$x = x_0$两侧$f’(x),f’’(x)$是否变号，而不须考虑$f’(x),f’’(x)$是否存在就可判定$x = x_0$是否是$f(x)$的极值点与拐点

$f(x)$在$x = x_0$不可导,$x = x_0$与$(x = f(x_0))$可以同时是$y=f(x)$的极值点与拐点，但对于可导函数，可以证明：若$x = f(x_0)$是$y=f(x)$的拐点，则$x = x_0$不可能是$f(x)$的极值点，因为第三充分条件

凹凸性

$f(x)$在$(a,b)$有定义。$\forall x_1,x_2\in(a,b)$，定义函数$f(\frac{x_1+x_2}{2})和\frac{f(x_2)+f(x_1)}{2}$：

若$f(\frac{x_1+x_2}{2})<\frac{f(x_2)+f(x_1)}{2}$，则称$f(x)$在$(a,b)$为$\color{salmon}{凹的(或凹弧)}$；
若$f(\frac{x_1+x_2}{2})>\frac{f(x_2)+f(x_1)}{2}$，则称$f(x)$在(a,b)为$\color{salmon}{凸的(或凸弧)}$。

导数定义：

设函数$f(x)$在$[a,b]$上连续，在$(a,b)$内具有一阶和二阶导数，那么：

若在$(a,b)$内$f’’(x) > 0$，则曲线$y=f(x)$在$[a,b]$上是凹的
在$(a,b)$内$f’’(x) < 0$，则曲线$y=f(x)$在$[a,b]$上是凸的

结合极值的第二充分条件理解，当$f’’(x)<0$时有极大值，自然是凸的

对于函数$f(x)$，如果在$x_0$点附近凹凸性发生了变化，则$x_0$点称为$\color{Salmon}{拐点}$

而求函数的拐点，则和求函数的极值点的步骤是一致的：

求$f’’(x)$
求出$f’’(x)=0$的实根与二阶不可导点
检查$f’’(x)$在$x_i$左、右两侧邻近的符号，那么当两侧的符号相反时，点$(x_i,f(x_i))$是拐点；当两侧的符号相同时，点$(x_i,f(x_i))$不是拐点

渐近线

水平渐近线

如果有：

$\lim_{x\to-\infty}f(x)=L\qquad\text{或}\qquad\lim_{x\to+\infty}f(x)=L$

那么直线$y=L$称为函数$y=f(x)$的水平渐近线。

垂直渐近线

如果有：

$\lim_{x\to x_0^-}f(x)=\pm\infty\qquad\text{或}\qquad\lim_{x\to x_0^+}f(x)=\pm\infty$

那么直线$x=x_0$称为函数$y=f(x)$的垂直渐近线。

斜渐近线

如果有：

$\lim_{x\to -\infty}[\ f(x)-(ax+b)\ ]=0\ \ \text{或}\ \ \lim_{x\to +\infty}[\ f(x)-(ax+b)\ ]=0$

那么直线$y=ax+b$称为函数$y=f(x)$的斜渐近线，其中$a=\lim_{x\to \infty}\frac{f(x)}{x}\qquad b=\lim_{x\to \infty}(f(x)-ax)$

如果能直接把函数写成$ax+b+o(x)$的形式，那么可以更快的得出结论，常常和泰勒公式一起使用

当确定斜渐进线存在，并过零点时，可直接假设斜渐近线斜率为$\lim_{x\to \infty} \frac{y}{x}=k$，然后将$k$带入方程求出具体的值，探后$\lim_{x\to \infty} y-kx=c$求出$c$的值，最终的渐近线即为$y=kx+c$

曲率

$K=\frac{1}{r}=\frac{\left|f''(x_0)\right|}{\left(1+\left(f'(x_0)\right)^2\right)^\frac{3}{2}}$