一元函数积分学

定积分

曲边梯形面积

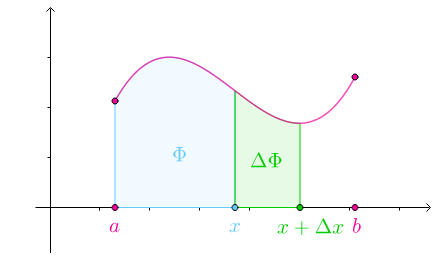
从曲边梯形的面积讲起：

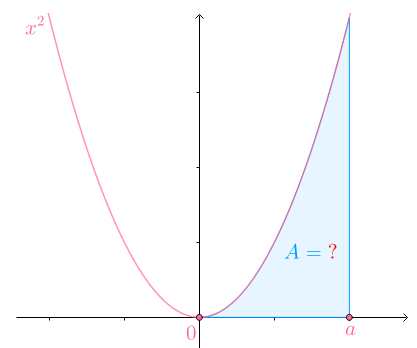
如果要求该梯形面积，可以把$[0,a]$均分为$n$份，以每一份线段为底，以这一份线段的右侧的函数值为矩形高度：

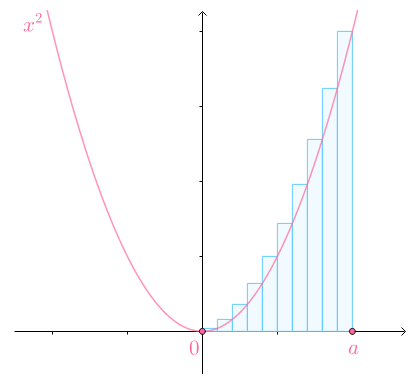
当$n\to\infty$的时候，矩形面积和就是曲面下的面积：

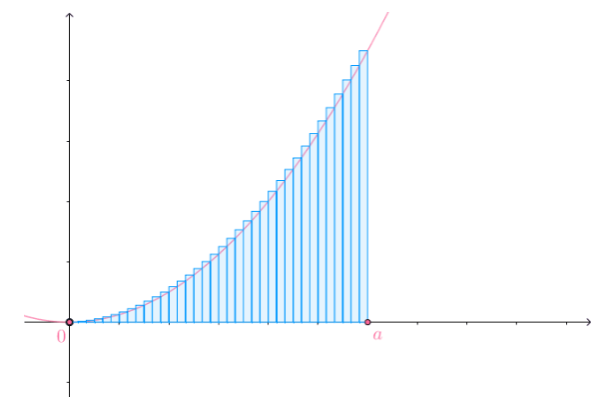
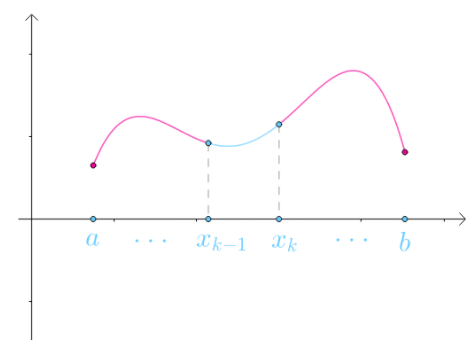
实际上，$[a,b]$不一定需要均分为$n$份，可以任意分割：

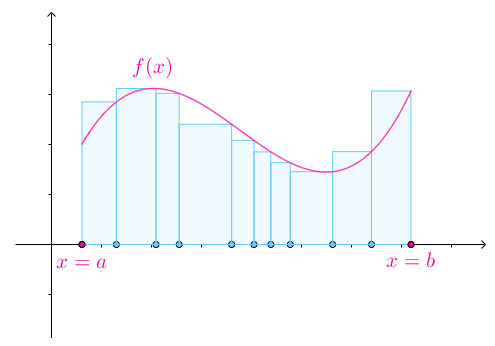
很显然用于分割区间的点符合：

$a < x_1 < x_2 < \cdots < x_{n-1} < b$

令$x_0=a,x_n=b$，那么集合：

$P=\{x_0, x_1, x_2, \cdots, x_{n}\}$

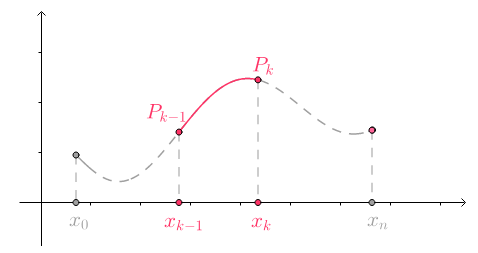
称为$[a,b]$的一个$\color{Salmon}{划分}$。划分$P$定义了$n$个子区间：

$[x_0, x_1], [x_1, x_2], \cdots,[x_{k-1}, x_k],\cdots, [x_{n-1}, x_n]$

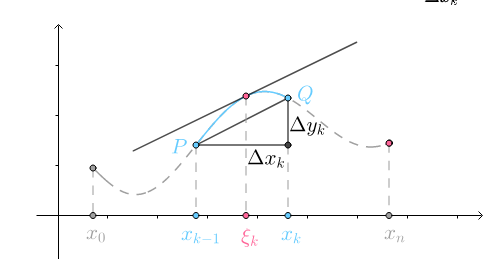
$[x_0, x_1]$称为第$1$个子区间，更一般的$[x_{k-1},x_k]$被称为第$k$个子区间

第$k$个子区间的长度为$\Delta x_k=x_k-x_{k-1}$：

对于某一个划分$P$，在其第$k$个子区间内随便选一个数$\xi_k$：

以$f(\xi_k)$作为矩形的高：

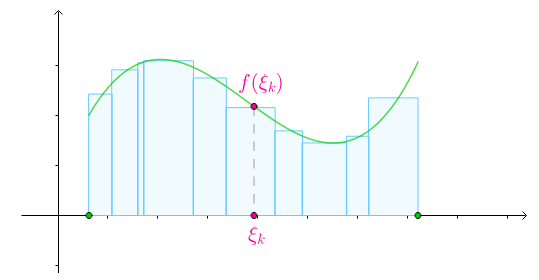
那么矩形的高度也可以是任意的：

黎曼和

根据以上的推导，可以得出这样的结论：

设函数$f(x)$在$[a,b]$上有定义，在$[a,b]$上任意插入若干个分点：

$a=x_0 < x_1 <x_2 ... < x_n =b$

这些分点的集合：

$P=\{x_0, x_1, x_2, \cdots, x_{n}\}$

称为$[a,b]$的一个$\color{Salmon}{划分}$。划分$P$定义了$n$个子区间：

$[x_0, x_1], [x_1, x_2], \cdots, [x_{n-1}, x_n]$

它们的长度依次为：

$\Delta x_1=x_1-x_0,\Delta x_2=x_2-x_1,\cdots,\Delta x_n=x_n-x_{n-1}$

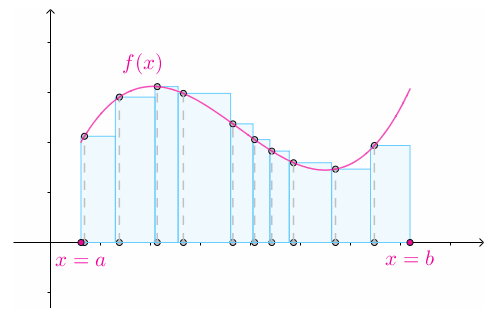
在每个子区间$[x_{k-1},x_k]$上任取选取一个数$\xi_k，以[x_{k-1},x_k]$为底，$f(\xi_k)$为高构造矩形，这些矩形的和：

$A_n=\sum_{k=1}^{n}f(\xi_k)\Delta x_k$

称为$f$在$[a,b]$上的$\color{Salmon}{黎曼和}$

随着$[a,b]$的划分不断变细，所有子区间的长度趋于$0$时，黎曼和不断地逼近曲边梯形的面积

严格定义

设函数$f(x)$在$[a,b]$上有定义，对于$[a,b]$上的任意划分$P$，$\xi_k$为子区间$[x_{k-1},x_k]$上任意选取的数，子区间$[x_{k-1},x_k]$的长度为$\Delta x_k$，记：

$\lambda=max\{\Delta x_1,\Delta x_2,...,\Delta x_n\}$

如果当$\lambda\to 0$时

$S=\sum_{i=1}^{n} f\left(\xi_{i}\right) \Delta x_{i}$

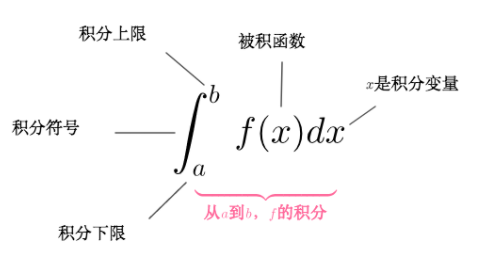
的极限总是存在，且与闭区间$[a,b]$的分法及点$\xi_i$的取法无关，那么称这个极限$I$为函数$f(x)$在区间$[a,b]$上的定积分，记做$\int_{a}^{b}f(x)dx$,即

$\int_{a}^{b} f(x) \mathrm{d} x=I=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}\right) \Delta x_{i}$

其中$a$为$\color{Salmon}{积分下限}$，$b为\color{Salmon}{积分上限}$，$I$为$f(x)$在$[a,b]$上的$\color{Salmon}{定积分}$，$x$为$\color{Salmon}{积分变量}$

$\lambda \to 0$的意思是$\Delta x\to 0$，让黎曼和等于曲边梯形的面积

性质

可积的充分条件：

如果$f(x)$在$[a,b]$上连续，则$f(x)$在$[a,b]$上可积：
如果$f(x)$在$[a,b]$上有界，且只有有限个间断点，则$f(x)$在$[a,b]$上可积
如果$f(x)$在$[a,b]$上仅有有限个第一类间断点，则$f(x)$在$[a,b]$上可积

所以连续一定可积，可积不一定连续

齐次性：

$\int_{a}^{b}cf(x)\textrm{d}x=c\int_{a}^{b}f(x)\textrm{d}x,c\in\mathbb{R}$

这点也不难理解，相同的划分、以及相同的方式选取$\xi_k$，让$f(\xi_k)$扩大了$c$倍，自然面积也会扩大$c$倍

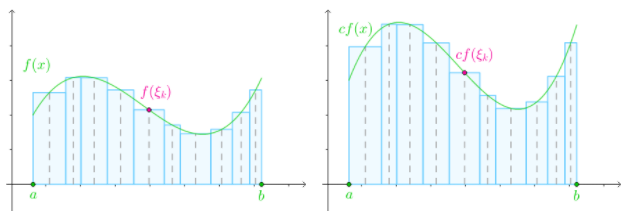
可加性：

$\int_{a}^{b}[f(x)+g(x)]\textrm{d}x=\int_{a}^{b}f(x)\textrm{d}x+\int_{a}^{b}g(x)\textrm{d}x$

面积的正负：

区间$[a,b]$上$f(x) < 0$，那么：

$\int_{a}^{b}f(x)\textrm{d}x < 0$

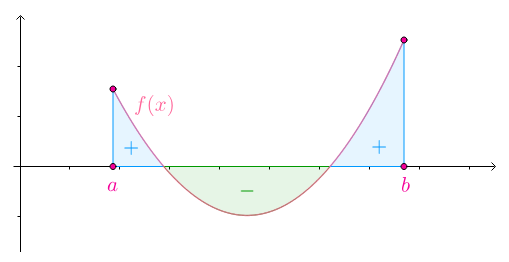
关于这点，可以延伸出来其他的形式，比如

$\int_{a}^{b}f(x)\textrm{d}x < c\qquad c是常数$

可以将$c$积分成区间内的一个其他常数$d$，然后将其换位如下形式：

$\int_{a}^{b}f(x)-d\quad\textrm{d}x <0$

这样就可以判断$f(x)-d$在区间$[a,b]$之间的单调性来判断其面积的正负了

面积的大小：

设$a < b$，如果在区间$[a,b]$上$f(x) > g(x)$，那么：

$\int_{a}^{b}f(x)\textrm{d}x > \int_{a}^{b}g(x)\textrm{d}x$

面积的分解：

设$a < c < b$，则：

$\int_{a}^{b}f(x)\textrm{d}x=\int_{a}^{c}f(x)\textrm{d}x+\int_{c}^{b}f(x)\textrm{d}x$

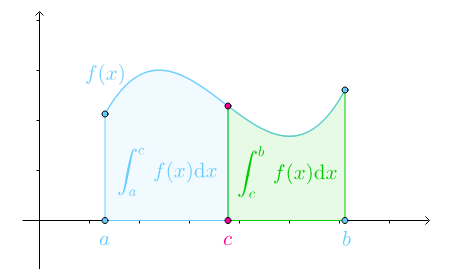
交换积分上下限，符号改变

$\int_{a}^{b}f(x)\textrm{d}x = -\int_{b}^{a}f(x)\textrm{d}x$

上下限一致，积分为0

$\int_{a}^{a}f(x)\textrm{d}x=0$

奇偶性

若$f(x)$是奇函数，则$\int^x_0f(t)dt$是偶函数，偶函数$\int^a_{-a}f(x)dx=2\int^a_0f(x)dx$

若$f(x)$是偶函数，则$\int^x_0f(t)dt$是奇函数，奇函数$\int^a_{-a}f(x)dx=0$

常见的奇函数有：$sinx，tanx，arcsinx，arctanx，ln\frac{1-x}{1+x}，ln(x+\sqrt{1+x^2})，\frac{e^x-1}{e^x+1}，f(x)-f(-x)$

常见的偶函数有：

$x^2，|x|，f(x)+f(-x)$

不等式

$|\int^b_af(x)dx|≤\int^b_a|f(x)|dx$

推导：

$(\int^a_bg(x)f(x)dx)^2≤\int^a_bg(x)^2dx·\int^a_bf(x)^2dx$

积分中值定理

设$a < b$，$M$和$m$分别是函数$f(x$)是区间$[a,b]$上的最大值和最小值，则：

$m\le\frac{1}{b-a}\int_{a}^{b}f(x)\textrm{d}x\le M$

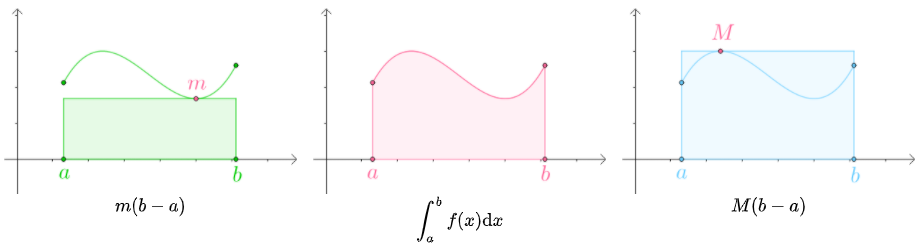
这是很显然的事实，故可以推导出，在$m(b-a)$到$M(b-a)$的过程中，必有一个矩形的面积和曲边梯形的面积相同

积分中值定理：

如果函数$f(x)$在积分区间$[a,b]$连续，那么在$[a,b]$上至少存在一点$\xi$，使下式成立：

$\int_a^bf(x)dx=f(\xi)(b-a),\xi\in[a,b]$

如果函数$f(x),g(x)$在$[a,b]$上连续，$g(x)$不变号，则：

$\int^b_af(x)g(x)dx=f(c)\int^b_ag(x)dx\qquad a≤c≤b$

微积分基本定理

积分上限函数

如果一个定积分的上限不确定，而是一个可以改变的值

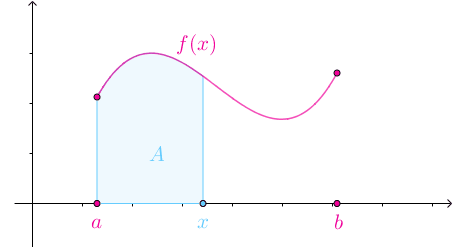
不同的$x$对应不同的$A$，所以这是一个面积函数$A(x)$

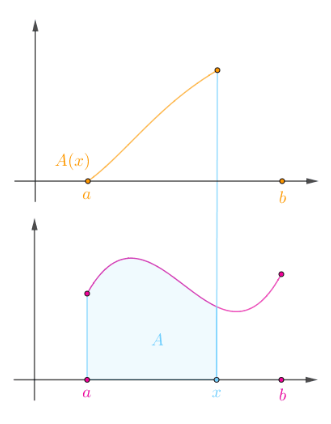
这个面积函数又称为$\color{Salmon}{积分上限函数}$，可以用定积分表示如下：

$A(x)=\int_a^x f(t)\textrm{d}t$

连续性：只要$f(x)$在区间$[a,b]$上可积，则存在积分上限函数$F(x)=\int^x_af(t)dt$在$[a,b]$上连续

$f(x)连续\Longrightarrow f(x)可积\Longrightarrow 上限函数F(x)连续$

如果$f(x)$在$[a,b]$上除点$x=x_0\in(a,b)$外均连续，则在点$x=x_0$处

如果连续，那么一定可导 $F’(x_0)=f(x_0)$ (符合原函数存在定理)

如果可去，那么一定可导 $F’(x_0)=\lim_{x\to x_0}f(x)$

如果跳跃，那么是连续但不可导，且$F’_+(x_0)=f(x_0^+)\qquad F’_-(x_0)=f(x_0^-)$

这和原函数存在定理并不冲突，只有$f(x_0)$连续的时候，$F(x_0)$才是原函数，在可去和跳跃间断点的情况下不是

如果$f(x)$是奇函数，则$\int_0^x f(t)\textrm{d}t$是偶函数

如果$f(x)$是偶函数，则$\int_0^x f(t)\textrm{d}t$是奇函数

积分上限函数的导数：$\int_0^{\phi(x)}f(t)dt$ ，$\phi (x)$是$n$阶，$f(t)$是$m$阶，这个积分就是$x$的$n+nm=n(m+1)$阶

第一基本定理

如果函数$f(x)$在区间$[a,b]$上连续，那么积分上限的函数：

$\Phi(x)=\int_a^x f(t)dt$

在$[a,b]$上可导，导数为：

$\Phi'(x)=\frac{d}{dx}\int_a^xf(t)dt=f(x),(a \leq x \leq b)$

证明过程

对$\Phi(x)$的求导，也就是求面积函数的变化率，增量$\Delta x$对应的面积$\Delta\Phi$为：

根据微积分的思想，当$\Delta x$足够小时，下面这个矩形面积约等于$\Delta\Phi$，即:

$f(x)\Delta x ≈\Delta \Phi$ $\frac{\Delta\Phi}{\Delta x}\approx f(x)$

进而两边取极限：

$\lim_{\Delta x \to 0}\frac{\Delta\Phi}{\Delta x}=\lim_{\Delta x \to 0}f(x)\implies \Phi'(x)=f(x)$

此定理之所以叫做“微积分第一定理”，是因为它说明了，$f(x)$在$[a,b]$上连续时，积分与求导（或者说，与微分）之间是互逆的，奠定了微积分的基础：

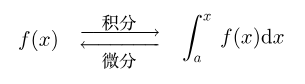
第一定理在积分和微分直接架起了桥梁，同样可写成

$f(x)=\int^x_a f'(x)dx$

和微分中值定理一样，为证明题提供了方便的工具

原函数：

如果在区间$I$上，可微函数$F(x)$都有：

$F'(x)=f(x)\quad或\quad \textrm{d}F(x)=f(x)\textrm{d}x$

那么函数$F(x)$就称为$f(x)$（或$f(x)\textrm{d}x$）在区间$I$上的一个$\color{Salmon}{原函数}$

所以在满足微积分第一基本定理时有：

第二基本定理

也叫作牛顿—莱布尼茨公式：

$f(x)$在$[a,b]$上连续，$F(x)$是$f(x)$的一个原函数，那么：

$\int_a^b f(x)\textrm{d}x=F(b)-F(a)$

也可以记作：

$\int_a^b f(x)\textrm{d}x=[F(x)]_a^b$

不定积分

原函数存在定理

定理1：

如果函数$f(x)$在区间$[a,b]$上连续，那么积分上限的函数：

$\Phi(x)=\int_a^x f(t)dt$

就是$f(x)$在$[a,b]$上的一个原函数。

这个定理说明了：

$连续函数 \implies 有原函数$

但这不是充要条件，某些间断函数同样也能有原函数

定理2：

如果$f(x)$在区间$[a,b]$上有第一类间断点，则$f(x)$在区间$I$上没有原函数

这个定理说明了：

$有第一类间断点\implies无原函数$

有原函数和可积之间并没有联系

定义

如果改变积分的下限：积分区间从$[a,x]$，变为$[a’,x]$

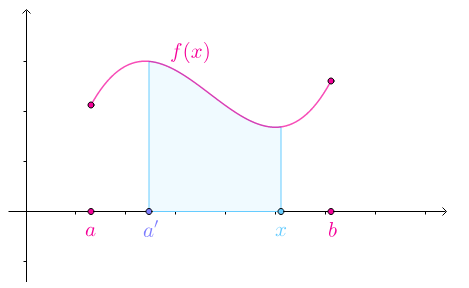
很显然有：

$\int_{a'}^x f(t)\textrm{d}t=\int_a^x f(t)\textrm{d}t-\int_a^{a'} f(t)\textrm{d}t$

而定积分为一个常数：

$C=\int_a^{a'} f(t)\textrm{d}t$

所以，调整下限之后的积分上限函数和$\Phi(x)$相差一个常数：

$\int_{a'}^x f(t)\textrm{d}t=\Phi(x)-C$

根据求导法则：

$(\int_{a'}^x f(t)\textrm{d}t)'=(\Phi(x)-C)'=f(x)$

依然是一个原函数。

原函数有很多。把所有的原函数定义为：

如果$F(x)$是$f(x)$在区间$I$上的一个原函数，那么$F(x)+C$就是$f(x)$的$\color{Salmon}{不定积分}$，即：

$\int f(x)\textrm{d}x=F(x)+C,C\in\mathbb{R}$

并且不定积分$\int f(x)dx$表示了$f(x)$的所有原函数

根据原函数存在定理，不定积分如果是分段函数，那么要考虑都在分段点的连续问题，需要设定符合条件的$C$

基本积分公式

三角函数的积分

$\int\cos x\textrm{d}x=\sin x+C\qquad \int\sin x\textrm{d}x=-\cos x+C\qquad$ ${\color{red}{\int\tan x\textrm{d}x=\ln|\sec x|+C}=-ln|cosx|+C}\qquad \int\cot x\textrm{d}x=ln|sinx|+C$ ${\color{red}\int\sec xdx=ln|secx+tanx|+C} \color{red}\qquad\int\csc xdx=ln|tan\frac{x}2{}|+C=ln|cscx-cotx|+C$ $\int\sec^2x\textrm{d}x=\tan x+C\qquad \int\csc^2x\textrm{d}x=-\cot x+C\\$ $\int\sec x\tan x\textrm{d}x=\sec x+C\qquad \int\csc x\cot x\textrm{d}x=-\csc x+C\quad\\$

推导过程

$\begin{aligned} \int secxdx=\int \frac{cos}{1-sin^2x}dx=\int \frac{1}{(1+sinx)(1-sinx)}dsinx\\ =\frac{1}{2}ln|\frac{1+sinx}{1-sinx}|+C\\ =ln\sqrt\frac{1+sinx}{1-sinx}+C\\ =ln\sqrt\frac{(1+sinx)^2}{1-sin^2x}+C\\ =ln\frac{1+sinx}{cosx}+C\\ =ln|secx+tanx|+C\\ \end{aligned}$ $\begin{aligned} \int\csc xdx=∫\frac{1}{sinx}dx =∫\frac{1}{2sin(\frac{x}{2})cos (\frac{x}{2})}dx\\ =∫\frac{1}{sin(\frac{x}{2})cos (\frac{x}{2})}d(\frac{x}{2})\\ =∫\frac{1}{tan\frac{x}{2}}·sec^2(\frac{x}{2})d(\frac{x}{2})\\ =∫\frac{1}{tan(\frac{x}{2})}d(tan\frac{x}{2})\\ =ln|tan\frac{x}{2}|+C \end{aligned}$

指数函数的积分

$\int x^n\textrm{d}x=\frac{x^{n+1}}{n+1}+C,(n\neq -1)\\$ $\int a^x\textrm{d}x=\frac{a^x}{\ln a}+C\\$ $\int e^x\textrm{d}x=e^x+C\\$ $\int\frac{1}{x}\textrm{d}x=\ln |x|+C$

分式的积分

$\int\frac{1}{\sqrt{a^2-x^2}}\textrm{d}x=\arcsin \frac{x}{a}+C\qquad \\$ $\color{red} \int\frac{1}{\sqrt{x^2+a^2}}\textrm{d}x=ln(x+\sqrt{x^2+a^2})+C\qquad \\$ $\int\frac{1}{\sqrt{x^2-a^2}}\textrm{d}x=ln|x+\sqrt{x^2-a^2}|+C\qquad \\$ $\int\frac{1}{a^2+x^2}\textrm{d}x=\frac{1}{a}\arctan\frac{x}{a}+C\qquad \\$ $\color{red} \int\frac{1}{x^2-a^2}dx=\frac{1}{2a}ln|\frac{x-a}{x+a}|+C\qquad$ $\color{red} \int\frac{1}{a^2-x^2}dx=\frac{1}{2a}ln|\frac{a+x}{a-x}|+C\qquad$ $\color{red}{\int\sqrt{1+x^2}dx=\frac{1}{2}x\sqrt{1+x^2}+\frac{1}{2}ln|x+\sqrt{1+x^2}|+C}$

推导过程

推导过程如下：

根据第二类换元法，$x=atant$

$\begin{align*} \int\frac{1}{\sqrt{x^2+a^2}}\textrm{d}x \\ &=\int\frac{d(atant)}{\sqrt{a^2tan^2t+a^2}}\\ & =\int\frac{asec^2t}{a\sqrt{tan^2t+1}}dt\\\ &=\int sectdt\\ &=ln(sect+tant)+C\\ & =ln(\sqrt{tant^2+1}+tant)+C\\ & =ln(\sqrt{\frac{x^2}{a^2}+1}+\frac{x}{a})+C\\ &=ln\frac{\sqrt{(x^2+a^2)+x}}{a}+C\\ &=ln(\sqrt{x^2+a^2}+x)-lna+C\\ &=ln(\sqrt{x^2+a^2}+x)+C \end{align*}$ $\begin{align*} \int\frac{1}{x^2-a^2}dx=\int\frac{1}{(x-a)(x+a)}dx \\=\frac{1}{2a}\int\frac{1}{x-a}-\frac{1}{x+a}dx \\=\frac{1}{2a}ln|\frac{x-a}{x+a}|+C \end{align*}$ $\begin{align*} \int\frac{1}{a^2-x^2}dx=\ \int\frac{\frac{1}{2a}[(a+x)(a-x)]}{(a-x)(a+x)}dx \\=\frac{1}{2a}\int\frac{1}{a-x}+\frac{1}{a+x}dx \\=\frac{1}{2a}ln|\frac{a+x}{a-x}|+C \end{align*}$ $\begin{align*} {\color{red}{\int\sqrt{1+x^2}dx}} \\&=x\sqrt{1+x^2}-\int x·\frac{x}{\sqrt{1+x^2}}dx\\ &=x\sqrt{1+x^2}-\int\frac{1+x^2-1}{\sqrt{1+x^2}}dx \\&=x\sqrt{1+x^2}-{\color{red}{\int\sqrt{1+x^2}dx}}+\int\frac{1}{\sqrt{1+x^2}}d \\&=\frac{1}{2}x\sqrt{1+x^2}+\frac{1}{2}ln|x+\sqrt{1+x^2}|+C \end{align*}$

分式积分$\int \frac{f(x)}{g(x)}dx$的常见类型

$\frac{f(x)}{g(x)}$是一整个根式的话，可以将根式代换成另一个未知数$t$，再进行积分，如果是根号下$\sqrt{1-x}$之类的形式，可以用三角函数代换，比如用$x=sin^2t$
如果$g(x)$是两个多项式相减或相加，考虑将其化为相乘的形式，再将其拆开，比如$x^3-1=(x-1)(x^2+x+1)$，如果是相乘的形式，直接考虑拆开
如果$g(x)$是一整个根式的话，观察根式内未知数的形式，如果根式内只是$\sqrt{a+x}$考虑直接进行换元，因为很好化简，$d\sqrt{a+x}=\frac{1}{2\sqrt{a+x}{}}$，或者是说$e^x$在分子，也可以直接换元，如果根式内是$\sqrt{a+x^2}$的形式，那就考虑进行三角函数变换
如果$g(x)$是一整个根式，但是根式里面是多项式$\sqrt{x+x^2}$的形式，考虑将根号下化为完全平方式，再换元
如果$g(x)$是低次×高次的形式，可以将低次升阶到高次，从而使未知数的次统一，比如$\frac{1}{x\sqrt{x^4+1}}$，这个$x$很容易升阶为$x^4$，分子分母都乘$x^3$,然后将分子上的$x^3$积进去就行了然后将根式$\sqrt{1+x^4}=t$进行换元，即可求解
在区间$[0,1]$上使用三角代换可能有方便
针对无穷积分的换元法，考虑到$\frac{1}{t}$的代换

对于

$\int\frac{sinx或cosx}{asinx+bcosx}dx$

形式的分式，可以使用如下技巧：

$sinx=a(sinx+cosx)+\beta(sinx+cosx)'=(a-\beta)sinx+(a+\beta)cosx$ $\begin{cases}a-\beta=1\\ a+\beta=0 \end{cases}\implies a=\frac{1}{2},\beta=-\frac{1}{2}$

所以可以分解成

$I=\int\frac{asinx+bcosx}{asinx+bcosx}dx+\int\frac{(asinx+bcosx)'}{asinx+bcosx}dx$

的形式

对于

$\int\frac{1}{asinx+bcosx}dx$

的形式，利用辅助角公式：

$a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+\alpha)\\ 其中\alpha=\arctan\frac{b}{a}\\$

那么原式化为：

$I(a,b)=\frac{1}{\sqrt{a^2+b^2}}\int\frac{dx}{sin(x+\alpha)}=\frac{1}{\sqrt{a^2+b^2}}\int csc(x+\alpha)d(x+\alpha)$

而已知：

$\int\csc xdx=ln|tan\frac{x}2{}|+C$

故：

$I(a,b)=\frac{1}{\sqrt{a^2+b^2}}ln|tan\frac{x+\alpha}{2}|+C$

对于

$\int\frac{1}{a^2sin^2x+b^2cos^2x}dx$

的形式

此时将分式上下同除一个$cos^2x$，化为

$\int\frac{sec^2x}{a^2tan^2x+b^2}dx=\frac{1}{a}\int\frac{d(atanx)}{a^2tan^2x+b^2}$ $I=\frac{1}{ab}arctan\frac{atanx}{b}+C$

分解因式法

当积分形式如下时,可以被分解因式：

$\int\frac{c}{f(x)^2g(x)}dx=\int \frac{A}{f(x)}+\frac{B}{f^2(x)}+\frac{C}{g(x)}dx$

如果$g(x)$是$1$次方程假设为$C$，如果是$2$次，就假设为$Cx+D$

积分技巧

第一类换元法

设$f(u)$具有原函数$F(u)$，$u=u(x)$可导，则有换元公式：

$\int f[\underbrace{u(x)}_{\color{skyblue}{u}}]\underbrace{u'(x)\textrm{d}x}_{\color{salmon}{\textrm{d}u}}=\int f(\color{skyblue}{u})\color{salmon}{\textrm{d}u}=F(u)+C$

第二类换元法

设$x=x(t)$是单调的可导函数，且$x’(t)\neq 0$，则$t$可以用$x$来表示，即有反函数：

$t=t(x)$

如果有：

$\int f(x)\textrm{d}x\xrightarrow{\quad 换元x=x(t)\quad}\int f[x(t)]x'(t)\textrm{d}t=F(t)+C$

则：

$\int f(x)\textrm{d}x=F(t(x))+C$

常用的换元法有：

$\quad \qquad\sqrt{a^2-x^2}\qquad x=asint(acost)\\$ $\sqrt{a^2+x^2}\qquad x=atant\\$ $\sqrt{x^2-a^2}\qquad x=asect$

区间简化公式：诀窍是$x-\frac{a+b}{2}=\frac{b-a}{2}sint$

$\int_{a}^{b} \sqrt{(x-a)(b-x)}dx=\frac{(b-a)^2}{8}\pi$

分部积分法

$f(x),g(x)$皆为可导函数，有：

$\int f(x)g'(x)dx=f(x)g(x)-\int g(x)f'(x)dx$

或设$u=f(x),v=g(x)$，上式可以写作：

$\int udv=uv-\int vdu$

多项式和指数或三角函数相乘，把三角函数和指数凑进去，即当做$g’(x)$

多项式和对数或反三角函数相乘，把多项式凑进去

对于某些积分$I=\int^a_bf(x)dx$难以处理时，有时通过变形将$I$变为另一种形式$I=\int^a_bg(x)dx$的形式，然后把两者结合在一起：

$2I=\int^a_b[f(x)+g(x)]dx$

若该积分易处理，则问题解决：

类型1

$I=\int^b_0f(x)dx\qquad 令x=b-t\implies\int_0^bf(b-t)dt=\int^b_0f(b-x)dx$ $2I=\int^b_0[f(x)+f(b-x)]dx$

类型2
$I=\int^a_{-a}f(x)dx \quad 令x=-t\implies\int^a_{-a}f(-t)dt$ $2I=\int^a_{-a}[f(x)+f(-x)]dx$

实际上以上方法都基于区间不变公式：

$\int_a^bf(x)dx\stackrel{x=a+b-t}{\longrightarrow}\int^b_af(a+b-t)dt$

常见的可积函数积分

有理函数积分$\int R(x)dx$

一般是两个多项式的除法，常常将$R(x)$拆成两个真分式之和

三角有理式积分$\int R(sinx,cosx)dx$

一般方法是万能代换，令$tan\frac{x}{2}=t$

$\int R(sinx,cosx)dx=\int R\left(\frac{2t}{1+t^2},\frac{1-t^2}{1+t^2}\right)\cdot\frac{2}{1+t^2}dt.$

特殊方法(变形，换元，分部)

如果$R(-sinx,cosx)=-R(sinx,cosx)$，则令$u=cosx$

如果$R(sinx,-cosx)=-R(sinx,cosx)$，则令$u=sinx$

如果$R(-sinx,-cosx)=-R(sinx,cosx)$，则令$u=tanx$

简单无理函数积分

对于不定积分 $\int R(x,\sqrt[n]\frac{ax+b}{cx+d})dx)$ ,令$\sqrt[n]\frac{ax+b}{cx+d}dx=t$

计算公式：

$\int_{0}^{\frac{\pi}{2}}\sin^{n}x dx=\int_{0}^{\frac{\pi}{2}}\cos^{n}x dx=\begin{cases}\frac{n-1}{n}\frac{n-3}{n-2}\frac{n-5}{n-4}...\frac{1}{2}\frac{\pi}{2}(当n为偶数时)\\\\ \frac{n-1}{n}\frac{n-3}{n-2}\frac{n-5}{n-4}...\frac{2}{3}(当n为奇数时)\end{cases}$ $\int^{\pi}_0cos^nxdx=\begin{cases}0\quad n为奇数\\ 2\int^{\frac{\pi}{2} }cos^nxdx \quad n为偶数\end{cases}$ $\int^{2\pi}_0cos^nxdx=\int^{2\pi}_0sin^nxdx=\begin{cases}0\quad n为奇数\\ 4\int^{\frac{\pi}{2} }cos^nxdx \quad n为偶数\end{cases}$ $\int_{0}^{\pi}xf(sinx) dx=\frac{\pi}{2}\int_{0}^{\pi}f(sinx) dx=\pi\int_0^{\pi/2}f(sinx)dx$

反常积分

定义

积分区间包含正负无穷的，统称为$\color{Salmon}{无穷限的反常积分}$：

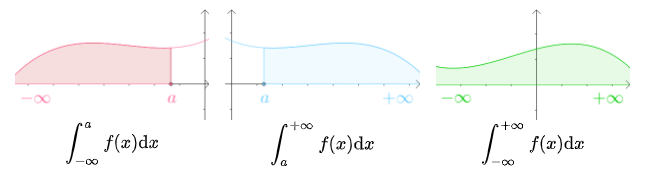
设函数$f(x)$在区间$(-\infty,a]$上连续，任取$t < a$，定义：

$\int_{-\infty}^{a}f(x)\textrm{d}x=\lim_{t\to-\infty}\int_{t}^{a}f(x)\textrm{d}x$

同样的，设函数$f(x)$在区间$[a,+\infty)$上连续，任取$t > a$，定义:

$\int_{a}^{+\infty}f(x)\textrm{d}x=\lim_{t\to+\infty}\int_{a}^{t}f(x)\textrm{d}x$

还有，设函数$f(x)$在区间$(-\infty,+\infty)$上连续，则：

$\int_{-\infty}^{+\infty}f(x)\textrm{d}x=\int_{-\infty}^{a}f(x)\textrm{d}x+\int_{a}^{+\infty}f(x)\textrm{d}x$

审敛法

$\int_a^{+\infty}\frac{1}{x^p}\textrm{d}x=\begin{cases}\frac{a^{1-p}}{p-1},&p > 1\quad 收敛\\ +\infty, &p\le 1\quad 发散\end{cases}$

设函数$f(x)$在$[a,+\infty)$上连续，且$f(x) \ge 0$。

如果$\exists p > 1$，使得$\lim_{x\to+\infty}x^pf(x)=c < +\infty$，那么$\int_a^{+\infty}f(x)\textrm{d}x$收敛；
如果$\lim_{x\to+\infty}xf(x)=d > 0$或$\lim_{x\to+\infty}xf(x)=+\infty$，那么$\int_a^{+\infty}f(x)\textrm{d}x$发散。

诀窍在于根据$f(x)$的阶数假设$p$的值

无界函数的反常积分

如果函数$f(x)$在点$a$的任一邻域内都无界，那么点$a$称为函数$f(x)$的$\color{Salmon}{瑕点}$（或称为无界间断点）：

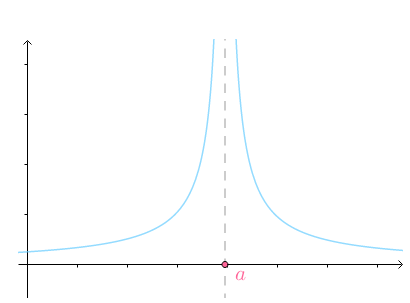
积分区间包含瑕点的积分称为$\color{Salmon}{无界函数的反常积分}$，又称为$\color{Salmon}{瑕积分}$：

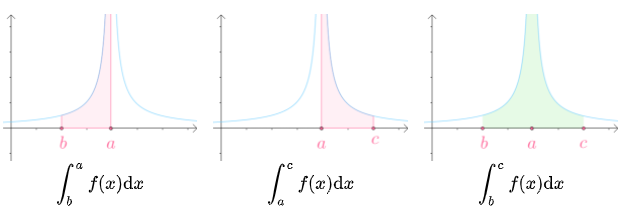
上述瑕积分定义如下。设函数$f(x)$在区间$[b,a)$上连续，点$a$为瑕点，任取$t < a$，定义：

$\int_{b}^{a}f(x)dx=\lim_{t\to a^{-}}\int_{b}^{t}f(x)dx$

同样的，设函数$f(x)$在区间$(a,c]$上连续，点$a$为瑕点，任取$t > a$，定义:

$\int_{a}^{c}f(x)dx=\lim_{t\to a^{+}}\int_{t}^{c}f(x)dx$

还有，设函数$f(x)$在区间$[b,a)\cup(a,c]$上连续，点$a$为瑕点，定义：

$\int_{b}^{c}f(x)dx=\int_{b}^{a}f(x)dx+\int_{a}^{c}f(x)dx$

无界函数的审敛法

和无穷极限的反常积分的结论相反

设函数$f(x)$在$(a,b]$上连续，且$f(x) \ge 0，x=a$为瑕点。

如果$\exists 0 < q < 1$，使得$\lim_{x\to a^+}(x-a)^qf(x)$存在，那么$\int_a^b f(x)\textrm{d}x$收敛；
如果$\lim_{x\to a^+}(x-a)f(x)=d > 0$或$\lim_{x\to a^+}(x-a)f(x)=+\infty$，那么$\int_a^b f(x)\textrm{d}x$发散

重要不定积分

$\int_1^{+\infty}\frac{1}{x^pln^q x}dx=\begin{cases}p > 1\quad q<1\quad 收敛\\ 其他情况\quad 发散\end{cases}$ $\int_0^{+\infty}x^ke^{-\lambda x}dx=\begin{cases}\lambda > 0\quad 收敛\\ \lambda\le 0\quad 发散\end{cases}$

证明：

$I=\int_1^{+\infty}\frac{dx}{x^pln^qx}=\int^e_1\frac{dx}{x^pln^qx}+\int^{+\infty}_e\frac{dx}{x^pln^qx}$ $lnx=ln[1+(x-1)]\sim x-1(x \to 1)$ $\lim_{x\to 1^+}\frac{\frac{dx}{x^pln^qx}}{\frac{dx}{(x-1)^q}}=1$

所以

$\int^e_1\frac{dx}{x^pln^qx}和\int_1^e\frac{dx}{(x-1)^q}敛散性相同$

所以$q<1$时，收敛

至于

$\int^{+\infty}_e\frac{dx}{x^pln^qx}敛散性和\int^{+\infty}_e\frac{dx}{x^p}一致$

所以$p>1$时收敛

$\Gamma$函数

$\Gamma$函数的定义：$Γ(\alpha)=\int_0^∞x^{a−1}e^{−x}dx\qquad a>0$

$\Gamma$函数的性质为：$\Gamma(\alpha+1)=\alpha\Gamma(a)\qquad\Gamma(n+1)=n!\qquad\Gamma(\frac{1}{2})=\sqrt{\pi}\qquad\Gamma(1)=1$

f(x)	$\int^{+\infty}_0f(x)dx$	$\Gamma$
$x^{-\frac{1}{2}}e^{-x}$	$\sqrt{\pi}$	$\Gamma(\frac{1}{2})$
$e^{-x}$	$1$	$ \Gamma(1) $
$x^{\frac{1}{2}}e^{-x}$	$\frac{\sqrt{\pi}}{2}$	$\Gamma(\frac{3}{2})=\Gamma(\frac{1}{2}+1)=\frac{1}{2}\Gamma(\frac{1}{2})$
$xe^{-x}$	$1$	$\Gamma(1+1)=\Gamma(1)$
$x^2e^{-x^2}$	$\frac{\sqrt{\pi}}{4}$	$\frac{1}{2}\Gamma(\frac{3}{2})$
$xe^{-x^2}$	$\frac{1}{2}$	$\frac{1}{2}\Gamma(1)$
$e^{-\frac{1}{2}x^2}$	$\frac{\sqrt{2\pi}}{2}$	$\sqrt{2}\Gamma(\frac{3}{2})$

针对$f(x)=x^2e^{-x^2}$，可使用换元法，$x^2=t$，

$\int_0^{+\infty}te^{-t}d\sqrt{t}=\frac{1}{2}\int_0^{+\infty}t^{\frac{1}{2}}e^{-t}dt=\frac{1}{2}\Gamma(\frac{3}{2})=\frac{\sqrt{\pi}}{4}$

因为$x^2$是偶函数，所以$\int_{-\infty}^{+\infty}f(x)dx=\frac{\sqrt{\pi}}{2}$

应用

平面图形的面积

直接用二重积分

$\iint_\limits{D}1\mathrm{d}A$

表示的就是积分域上图形的面积

旋转体体积

假设积分区域是$D$，绕直线$ax+by-c=0$旋转了一周

积分区域中心到直线的距离为：

$r(x,y)=\frac{|ax+by+c|}{\sqrt{a^2+b^2}}$

旋转体的周长是$C=2\pi r$，那么旋转体的体积就是

$V=2\pi\iint_\limits{D}r(x,y)\mathrm{d}A$

当区域$D$绕$x$轴旋转时，$r(x,y)=y$，体积为：

$V=2\pi\iint_\limits{D}r(x,y)\mathrm{d}A\implies2\pi\int_a^b dx\int _0^{f(x)}ydy\implies \pi\int_a^b f(x)^2dx$

当区域$D$绕$y$轴旋转时，$r(x,y)=x$，体积为：

$V=2\pi\iint_\limits{D}r(x,y)\mathrm{d}A\implies2\pi\int_a^b dx\int _0^{f(x)}xdy\implies2\pi\int^b_axf(x)dx$

弧长

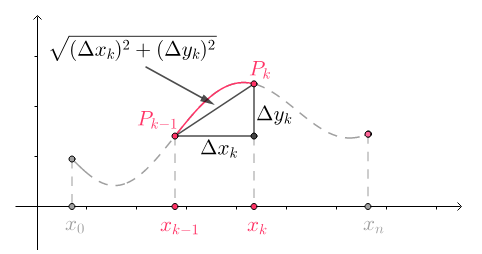
如果函数$y=f(x)在[a,b]$上有一阶连续导函数，那么称$y=f(x)$在$[a,b]$上是$\color{Salmon}{光滑}$的。光滑函数$y=f(x)$在$[a,b]$上的弧长为：

$\overparen{ab}=\int_a^b \sqrt{1+(f'(x))^2}\textrm{d}x$

定义$\color{Salmon}{弧微分}$：

$\textrm{d}s=\sqrt{1+(f'(x))^2}\textrm{d}x$

那么上式可以简写为：

$\overparen{ab}=\int_a^b \textrm{d}s$

证明过程

算弧线$y=f(x)$在$[a,b]$之间的长度，可以把它随机分为$n$个曲线段，用端点的连线来近似这些曲线段：

观察某子区间$[x_{k-1},x_k]$的弧长$\overparen{P_{k-1}P_k}$：

当$\Delta x_k=x_k-x_{k-1}$足够小的时候，$\overparen{P_{k-1}P_k}$近似等于$\overline{P_{k-1}P_k}$：

即：

$\overparen{P_{k-1}P_k}\approx \overline{P_{k-1}P_k}=\sqrt{(\Delta x_k)^2+(\Delta y_k)^2}$

$\overline{P_{k-1}P_k}$变换一下：

$\begin{aligned} \overline{P_{k-1}P_k} &=\sqrt{(\Delta x_k)^2+(\Delta y_k)^2}\\ \\ &=\frac{\sqrt{(\Delta x_k)^2+(\Delta y_k)^2}}{\Delta x_k}\Delta x_k\\ \\ &=\sqrt{1+\left(\frac{\Delta y_k}{\Delta x_k}\right)^2}\Delta x_k \end{aligned}$

如果$y=f(x)$可微，那么根据拉格朗日中值定理，可知有$\xi_k\in[x_{k-1},x_k]$，使得$f’(\xi_k)=\frac{\Delta y_k}{\Delta x_k}$（即$x=\xi_k$处的切线与$\overline{PQ}$平行）

所以：

$\overline{P_{k-1}P_k}=\sqrt{1+(f'(\xi_k))^2}\Delta x_k$

所以可以推出弧长为：

$\overparen{ab}=\int_a^b\underbrace{\sqrt{1+\left(f'(x)\right)^2}\textrm{d}x}_{用于近似弧长的线段长}$

参数方程下的弧长：

参数方程：

$\begin{cases} x=x(t)\\ y=y(t) \end{cases}$

如果$x’(t)、y’(t)$在$\alpha\le t\le\beta$上存在且连续，那么$\alpha\le t\le\beta$上的弧长为：

$\int_\alpha^\beta\sqrt{\left(x'(t)\right)^2+\left(y'(t)\right)^2}\textrm{d}t$

极坐标方程下的弧长

当曲线弧由极坐标方程

$\rho=\rho(\theta) \quad(\alpha \leqslant \theta \leqslant \beta)$

给出，其中$\rho(\theta)$在$[\alpha,\beta]$上具有连续导数，则由直角坐标与极坐标的关系可得

$\left\{\begin{array}{l}{x=x(\theta)=\rho(\theta) \cos \theta} \\ {y=y(\theta)=\rho(\theta) \sin \theta}\end{array}(\alpha \leqslant \theta \leqslant \beta)\right.$

这就是以极角$\theta$为参数的曲线弧的参数方程。于是，弧长元素为

$\mathrm{d} s=\sqrt{x^{\prime 2}(\theta)+y^{\prime 2}(\theta)} \mathrm{d} \theta=\sqrt{\rho^{2}(\theta)+\rho^{\prime 2}(\theta)} \mathrm{d} \theta$

从而所求弧长为

$s=\int_{\alpha}^{\beta} \sqrt{\rho^{2}(\theta)+\rho^{\prime 2}(\theta)} \mathrm{d} \theta$

旋转体表面积

已知弧长是

$\overparen{ab}=\int_a^b\underbrace{\sqrt{1+\left(f'(x)\right)^2}\textrm{d}x}_{用于近似弧长的线段长}$

那么可以用

$A=\int_a^b 2\pi f(x)\textrm{d}s=\int_a^b 2\pi f(x)\underbrace{\sqrt{1+(f'(x))^2}\textrm{d}x}_{弧微分\textrm{d}s}$

表示旋转体的表面积

需要考虑到内曲面和外曲面的问题

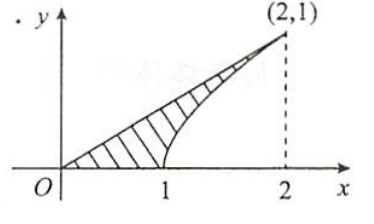
这种图形的表面积$S$为：$S_{外}+S_{内}$，$S_{外}$指的是$y=0.5x$在$[0,2]$上的表面积，而$S_{内}$指的是$y=\sqrt{x-1}$在$[1,2]$上的表面积

几何体公式

椭圆面积：$S=\pi a b$

圆锥体积：$V=\frac{1}{3}\pi r^2 h$

圆锥表面积：$S=πr²+πrl$

球的体积：$V=\frac{4}{3}\pi r^3$