常微分方程

定义

含有未知函数及其导函数的方程称为$\color{Salmon}{微分方程}$：

$\begin{array}{c|c|c} \hline &\quad未知数\quad&\quad例子\quad\\\hline \quad\color{SkyBlue}{方程}\quad&\quad x\quad&\quad 2x+1=3\quad\quad\\ \hline \quad\color{orange}{微分方程}\quad&\quad y\quad&\quad\frac{\mathrm{d}y}{\mathrm{d}x}+xy=2x\quad\\ \hline \end{array}$

微分方程中出现的导函数的最高阶数，叫做微分方程的$\color{Salmon}{阶}$

$n$阶微分方程的形式是：

$F(x,y,y',\cdots,y^{(n)})=0$

这里必须指出在方程中，$y^{(n)}$是必须出现的，而$x,y,y’,\cdots,y^{(n-1)}$等变量则可以不出现。

可分离变量的微分方程

如果一个一阶微分方程能写成：

$g(y)\mathrm{d}y=f(x)\mathrm{d}x$

的形式，这就是$\color{Salmon}{可分离变量的微分方程}$。

对其两边求不定积分：

$\int g(y)\mathrm{d}y=\int f(x)\mathrm{d}x$

分别得到$g(y)$和$f(x)$的原函数$G(y)$、$F(x)$，于是：

$G(y)=F(x)+C$

为此微分方程的解。

在解微分方程时，变量$x,y$地位可看做相同的，既可把$y$看作$x$的函数，又可把$x$看作$y$的函数

如果遇到复合函数，如$y’=cos(x+y)$的类型，考虑进行变量代换，将$x+y=u$，就变成了$u’=1+cosu$的形式，就是可分离变量的微分方程了

齐次方程

如果一阶微分方程可以写成：

$\frac{\mathrm{d}y}{\mathrm{d}x}=\varphi\left(\frac{y}{x}\right)$

的形式，那么称此方程为$\color{Salmon}{齐次方程}$。这个方程是可以通过 换元变换为可分离变量的微分方程的。

设$\frac{y}{x}=u$，那么就化成了：

$u+x\frac{du}{dx}=\varphi(u)$

最后换成是$\int udu=\int xdx$的形式

实际上，这种化简技巧并不局限于$\frac{y}{x}$的形式，比如$2yy’$的形式，就可以看做是$u=y^2，y’sec^2y$的形式，就可以看做是$u=tany$，根据导数形式灵活化简

方程

$xy''=y'+xsin\frac{y'}{x}$

解题步骤是：

$\begin{aligned} y''=\frac{y'}{x}+sin\frac{y'}{x}\\ p=y'\qquad \frac{dp}{dx}=\frac{p}{x}+sin\frac{p}{x}\\ u=\frac{p}{x}\qquad u+x\frac{du}{dx}=u+sinu\\ \int \frac{1}{sinu}du=\int\frac{1}{x}dx\\ ln|tan\frac{u}{2}|=ln|x|+C'_1 \end{aligned}$

解出：

$\begin{aligned} tan\frac{u}{2}=C_1x\\ tan\frac{y'}{2x}=C_1x\\ y'=2xarctanC_1x \end{aligned}$

再积分

$\begin{aligned} y=\int2xarctanC_1xdx+C_2=\int arctanC_1xdx^2+C_2\\ =x^2arctanC_1x-\frac{1}{C_1}\int\frac{C_1^2x^2+1-1}{1+(C_1x)^2}+C_2\\=x^2arctanC_1x-\frac{x}{C_1}+\frac{1}{C^2_1}arctanC_1x+C_2 \end{aligned}$

如果$C_1=0$，则$y=C_2$

可降阶方程(两阶微分方程)

因为常系数非齐次二阶方程和变系数二阶微分方程不存在通解，所以可降阶方程主要针对的是$\color{salmon}{两阶微分方程}$类型

$y’’=f(x)$类型

无论是齐次还是非齐次，对方程两边做两次积分即可解
$y’’=f(x,y’)$类型

需要讨论是常系数非齐次和变系数齐次or非齐次的类型

如果是变系数齐次方程，那么设$y’=P,y’’=\frac{dP}{dx}$，
$P'+f(x)P=0$
将二阶降阶为了自变量为$P$的一阶方程，形式就是可分离变量的微分方程，解出$y’=P$，之后再对$y’$积分，求出$y$的通解

$y’’=f(y,y’)$类型

设$y’=P,y’’=P\frac{dP}{dy}$

比如$3yy’’-2y’^2=0$
$\begin{aligned} 3ypp’-2p^2=0\\ 3yp'-2p=0\\ p'-\frac{2}{3y}p=0\\ p=C_1e^{-\int-\frac{2}{3y}dy}=C_1y^\frac{2}{3}\\ y^{-\frac{2}{3}}dy=C_1dx\\ 3y^\frac{1}{3}=C_1x+C_2 \end{aligned}$

线性微分方程

定义

对于微分方程：

$\mathcal{L}=a_0+a_1D+a_2D^2+a_3D^3+\cdots+a_nD^n$

$D$指的是对$y$求导的阶数

下式：

$\mathcal{L}(y)=f(x)$

称为$\color{Salmon}{线性微分方程}$。如果$f(x)$：

等于0：齐次线性微分方程
不等于0：非齐次线性微分方程

如果系数$a_0,a_1,\cdots,a_n$：

是常数：常系数线性微分方程
是函数：变系数线性微分方程

解的结构

对于二维齐次线性微分方程$y’’+p(x)y’+q(x)y=0$，解空间很明显是一个平面：

定理1：

如果$\boldsymbol{p_1},\boldsymbol{p_2},\cdots,\boldsymbol{p_n}$是$n$维齐次线性方程组：
$A\boldsymbol{x}=\boldsymbol{0}$
的解，并且它们$\color{Salmon}{线性无关}$，那么线性组合：
$\boldsymbol{p}=C_1\boldsymbol{p_1}+C_2\boldsymbol{p_2}+\cdots+C_n\boldsymbol{p_n}(C_1,C_2,\cdots,C_n\in\mathbb{R})$
是此方程组的$\color{Salmon}{通解}$。

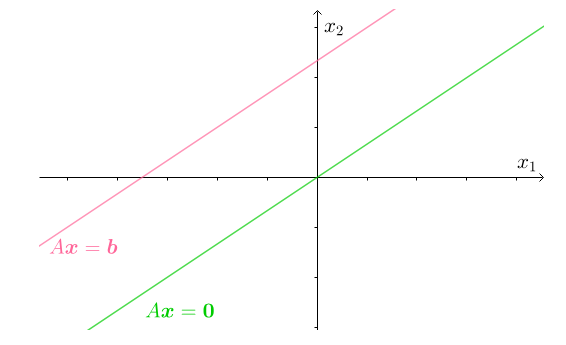
非齐次线性函数$a_1x_1+a_2x_2=b,b\ne 0$和齐次线性函数$a_1x_1+a_2x_2=0$，或者说齐次线性方程组$A\boldsymbol{x}=\boldsymbol{0}$与非齐次线性方程组$A\boldsymbol{x}=\boldsymbol{b}$，是平行的直线：

任取$A\boldsymbol{x}=\boldsymbol{0}$上的点$\boldsymbol{p_1}$，也任取$A\boldsymbol{x}=\boldsymbol{b}$上的点$\boldsymbol{p_2}$：

两者相加：

$\boldsymbol{p_3}=\boldsymbol{p_1}+\boldsymbol{p_2}$

也是$A\boldsymbol{x}=\boldsymbol{b}$上的点：

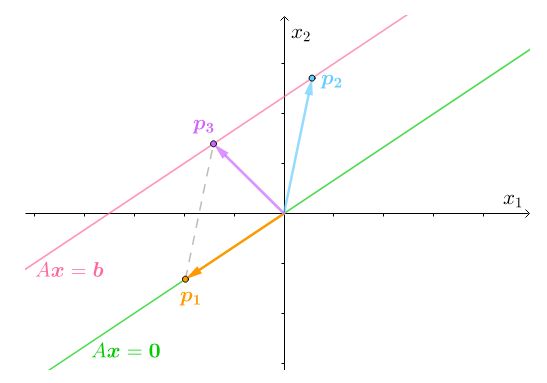
任意一个$A\boldsymbol{x}=\boldsymbol{0}$上的点，和$\boldsymbol{p_2}$相加，都是$A\boldsymbol{x}=\boldsymbol{b}$上的点：

定理2：

如果：
$\boldsymbol{p}=C_1\boldsymbol{p_1}+C_2\boldsymbol{p_2}+\cdots+C_n\boldsymbol{p_n}(C_1,C_2,\cdots,C_n\in\mathbb{R})$
是齐次线性方程组：$A\boldsymbol{x}=\boldsymbol{0}$的通解。

$\boldsymbol{p^*}$是非齐次线性方程组：$A\boldsymbol{x}=\boldsymbol{b}$的一个解，也称为$\color{Salmon}{特解}$，那么：
$\boldsymbol{p}+\boldsymbol{p^*}$
是非齐次线性方程组的所有解。

定理3：

非齐次方程的两个特解$p_1，p_2$相减是齐次微分方程的解
$p=p_1-p_2$

常系数线性微分方程

齐次(一阶，二阶)

一阶形式为：

$y'+py=0$

将变系数线性微分方程的通解替换为常系数,通解为：

$\color{red}y=Ce^{-\int P(x)\mathrm{d}x}=Ce^{-px}\quad$

某二阶常系数齐次线性微分方程：

$y''+py'+qy=0$

首先，欧拉发现不论$p、q是$什么，通解都具有以下形式：

$Y=C_1e^{r_1x}+C_2e^{r_2x}$

$r_1、r_2$是复数。那么可以合理假设$y=e^{rx}$，得到：

$y'=re^{rx},\quad y''=r^2e^{rx}$

回代到微分方程中，得到：

$(r^2+pr+q)e^{rx}=0$

要使等式成立，显然要使下式成立：

$r^2+pr+q=0$

这是一个一元二次方程，也被称为此微分方程的$\color{Salmon}{特征方程}$

可以用公式：

$r_{1,2}=\frac{-p\pm\sqrt{p^2-4q}}{2}$

求出$r_1、r_2$。有三种情况：

当$p^2-4q > 0，r_1、r_2$是不相等的实根：

$r_1=\frac{-p+\sqrt{p^2-4q}}{2},\quad r_2=\frac{-p-\sqrt{p^2-4q}}{2}$

当$p^2-4q = 0$：

$r_1=r_2=-\frac{p}{2}$

当$p^2-4q < 0$是不相等的复根：

$r_1=\alpha+\beta i,\quad r_2=\alpha-\beta i$

其中：

$\alpha=-\frac{p}{2},\quad \beta=\frac{\sqrt{4q-p^2}}{2}$

因此微分方程的通解也分为三种情况。

当$r_1\ne r_2$且是实根时，$y_1=e^{r_1x}、y_2=e^{r_2x}$都是微分方程的解，而且$\frac{y_2}{y_1}=\frac{e^{r_2x}}{e^{r_1x}}$不是常数，那么这两个解线性无关。

根据，线性微分方程解的结构，此时通解为：
$Y=C_1e^{r_1x}+C_2e^{r_2x}$
当$r_1=r_2=-\frac{p}{2}$时，只得到了一个解：
$y_1=e^{r_1x}$
通解为：
$Y=(C_1+C_2x)e^{r_1x}$
证明过程

因为要保证：
$\frac{y_2}{y_1}\ne 常数$
所以，必然：
$\frac{y_2}{y_1}=u(x)\implies y_2=u(x)e^{r_1x}$
现在就是要求出$u(x)$为多少。先求出：
$y_2'=e^{r_1x}\left(u'+r_1u\right),\quad y_2''=e^{r_1x}\left(u''+2r_1u'+r_1^2u\right)$
所以代入微分方程有：
$e^{r_1x}\left[\left(u''+2r_1u'+r_1^2u\right)+p\left(u'+r_1u\right)+qu\right]=0$
化简后得到：
$u''+(2r_1+p)u'+(r_1^2+pr_1+q)u=0$
由于$r_1$为特征方程的根，所以$r_1^2+pr_1+q=0$。又$r_1=-\frac{p}{2}$，所以$2r_1+p=0$，所以：
$u''=0$
随便选择一个满足此条件的函数，注意不能是常数函数，那就选$u(x)=x$吧，由此：
$y_2=xe^{r_1x}$
所以通解为：
$Y=(C_1+C_2x)e^{r_1x}$
当$r_1\ne r_2$且是复根时，$y_1=e^{(\alpha+\beta i)x}、y_2=e^{(\alpha-\beta i)x}$都是微分方程的解，只是这是复数函数。根据欧拉公式：
$y_1=e^{(\alpha+\beta i)x}=e^{\alpha x}e^{\beta xi}=e^{\alpha x}\left(\cos\beta x+i\sin\beta x\right)$ $y_2=e^{(\alpha-\beta i)x}=e^{\alpha x}e^{-\beta xi}=e^{\alpha x}\left(\cos\beta x-i\sin\beta x\right)$
$y_1、y_2$的线性组合依然是微分方程的解：
$\overline{y_1}=\frac{1}{2}\left(y_1+y_2\right)=e^{\alpha x}\cos\beta x$ $\overline{y_2}=\frac{1}{2i}\left(y_1-y_2\right)=e^{\alpha x}\sin\beta x$
$\overline{y_1}、\overline{y_2}$都是实值函数，且：
$\frac{\overline{y_1}}{\overline{y_2}}=\frac{e^{\alpha x}\cos \beta x}{e^{\alpha x}\sin \beta x}=\cot \beta x$
并非常数，即两者线性无关，所以通解为：
$Y=e^{\alpha x}\left(C_1\cos\beta x+C_2\sin\beta x\right)$

二阶常系数齐次线性微分方程的通解为：
$\begin{array}{c|c} \hline &\quad通解\quad\\ \hline \\ \quad 不相等的实根\ \ r_1,r_2\quad&\quad Y=C_1e^{r_1x}+C_2e^{r_2x}\quad \\ \quad 相等的实根\ \ r_1=r_2\quad&\quad Y=(C_1+C_2x)e^{r_1x}\quad\\ \quad 不相等的复根\ \ r_1,r_2\quad&\quad Y=e^{\alpha x}\left(C_1\cos\beta x+C_2\sin\beta x\right)\quad\\ \\ \hline \end{array}$

结论：已知特征方程为$\lambda ^2+b\lambda +c=0$，如果系数$b,c>0$，那么最后解出的$\lambda<0$，则$\lim_{x\to \infty} f(x)=0$

非齐次（一阶，特解二阶）

一阶：

$y’+py=f(x)$

将变系数线性微分方程的通解替换为常系数：

$\color{red} y=\left(\int Q(x)e^{\int p\mathrm{d}x}\mathrm{d}x+C\right)e^{-\int p\mathrm{d}x}= \left(\int f(x)e^{px}\mathrm{d}x+C\right)e^{-px}$

二阶：

$y’’+py’+qy=f(x)$

主要问题是解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程

当自由项是指数函数时：$(ae^ {\lambda x})$，假设特解为$x^k (ae^ {\lambda x})$，$k$为$\lambda$ 的$k$重根，$a$的值需要带入方程中运算

当自由项为线性函数时：$(ax+b)$，假设和特解为$y^*=x^{k}(a x+b)$，将$ax+b$带入方程中可定出$a$和$b$，$k$指$\lambda(0)$是特征方程的$k$重根

当自由项是三角函数时：$(cos\beta x,sin\beta x)$，假设特解为$y^*=x^{k}(a cos\beta x+bsin\beta x)$，将$acos\beta x,bsin\beta x$带入方程可定出$a$和$b$，$k$的值取决于$\lambda(0)+\beta i$是特征方程的$k$重根

其实线性函数和三角函数的都含有$e^{\lambda x}$，不过$\lambda$ 为0。如果出现$x^2e^x$的形式，说明微分方程至少是3阶

当自由项为指数函数乘多项式时：$e^{\lambda x}P_m(x)$，假设特解$y^*=x^kQ_m(x)e^{\lambda x}$，$k$指$\lambda$是特征方程的$k$重根

当自由项是三角函数乘多项式时：$e^{ax}[P_l(x)cos\beta x+P_nsin\beta x]$，假设特解$y^*=x^ke^{ax}[R_m(x)cos\beta x+R_m(x)sin\beta x]$，$m$的值取决于$l$和$n$的最高次，$k$指$\alpha+\beta i$是特征方程的$k$重根

变系数线性微分方程

变系数线性微分方程的解不一定能求出来，下面介绍几种可解的。

一阶变系数线性微分方程经过变形之后都可以写成如下的形式：

$\frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x)$

齐次（一阶）

先求它的齐次方程：

$\frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=0$

的解，很显然可以分离变量：

$\frac{\mathrm{d}y}{y}=-P(x)\mathrm{d}x$

两端积分，得：

$\ln|y|=-\int P(x)\mathrm{d}x+C_1$

改写下就得到了齐次方程的通解：

$\color{red}y=Ce^{-\int P(x)\mathrm{d}x}\quad (C=\pm e^{C_1})$

非齐次（一阶）

$\color{red} y=\left(\int Q(x)e^{\int P(x)\mathrm{d}x}\mathrm{d}x+C\right)e^{-\int P(x)\mathrm{d}x}$

证明过程

求非齐次方程：

$\frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x)$

的通解。假设：

$y=u(x)e^{-\int P(x)\mathrm{d}x}$

则：

$\frac{\mathrm{d}y}{\mathrm{d}x}=u'e^{-\int P(x)\mathrm{d}x}-uP(x)e^{-\int P(x)\mathrm{d}x}$

回代到非齐次方程中，得到：

$u'e^{-\int P(x)\mathrm{d}x}-uP(x)e^{-\int P(x)\mathrm{d}x}+P(x)ue^{-\int P(x)\mathrm{d}x}=Q(x)$

消去之后可得：

$u'e^{-\int P(x)\mathrm{d}x}=Q(x)\implies u'=Q(x)e^{\int P(x)\mathrm{d}x}$

两端积分，得：

$u(x)=\int Q(x)e^{\int P(x)\mathrm{d}x}\mathrm{d}x+C$

因此，非齐次方程的通解为：

$y=\left(\int Q(x)e^{\int P(x)\mathrm{d}x}\mathrm{d}x+C\right)e^{-\int P(x)\mathrm{d}x}$

一般拆开来写作：

$y=e^{-\int P(x)\mathrm{d}x}\int Q(x)e^{\int P(x)\mathrm{d}x}\mathrm{d}x+Ce^{-\int P(x)\mathrm{d}x}$

常考题型

最常见的题型如下：

已知$y’’+by’+cy=f(x)$，求其特解的形式，这种题求解的步骤的一般步骤是：

根据特征方程算出特征根($r_1.r_2$)
根据特征根和$f(x)$的形式，确定特解的形式(比如$x^ke^x(Acos\beta x+Bsin\beta x)$)
将特解带入进方程，求出待定系数的值(如果$A$或者$B$是$0$的话，特解形式就会改变)

其还有变种，有时候会给出$y’(0)$和$y’’(0)$的值，这种情况下，通解=特解+齐次解，然后将通解代入求出其通解

还有积分-微分方程的形式，如果对积分进行多次求导，将其化成微分方程的形式，然后根据积分的性质，得出初始条件，以求解最终的$C$值

例如：$f(x+y)=\frac{f(x)+f(y)}{1-f(x)f(y)}$，$f(xy)=yf(x)+xf(y)$的形式，常常和导数有关，解决此类题，要从导数的定义入手

$f'(x)=\frac{f(x+\Delta x)-f(x)}{\Delta x}$

其中$f(x+\Delta x)$根据题目给出的条件转换为对应的形式，然后就可求出$f’(x)$