8.5 ex4：bias vs variance

概述

在本练习的前半部分，你将实现正则化线性回归，用于预测水库中水位变化与水流出量之间的关系。在接下来的一半中，你将进行一些调试学习算法的诊断，并研究偏差与方差的影响。

必要的文件如下：

  • ex5.py - Python脚本，通过练习的步骤引导您
  • ex5data1.mat - 数据集
  • featureNormalize.py - 特征归一化函数
  • plotFit.py - 绘制多项式拟合图
  • trainLinearReg.py - 使用您的成本函数训练线性回归

需要完成的文件如下：

  • linearRegCostFunction.py - 正则化线性回归成本函数
  • learningCurve.py - 生成学习曲线
  • polyFeatures.py - 将数据映射到多项式特征空间
  • validationCurve.py - 生成交叉验证曲线

导入

1
2
3
4
5
6
7
8
9
10
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as scio
import linearRegCostFunction as lrcf
import trainLinearReg as tlr
import learningCurve as lc
import polyFeatures as pf
import featureNormalize as fn
import plotFit as plotft
import validationCurve as vc

加载和绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
# 加载训练数据
print('加载和可视化数据...')

# 从ex5data1加载数据：
data = scio.loadmat('ex5data1.mat')
X = data['X']
y = data['y'].flatten()
Xval = data['Xval']
yval = data['yval'].flatten()
Xtest = data['Xtest']
ytest = data['ytest'].flatten()

m = y.size

data数据集分为三个部分：

  • 用于模型学习的训练集：X, y
  • 用于确定正则化参数的交叉验证集：Xval, yval
  • 用于评估性能的测试集。这些是在训练期间模型未见过的“未知”示例：Xtest, ytest
1
2
3
4
5
6
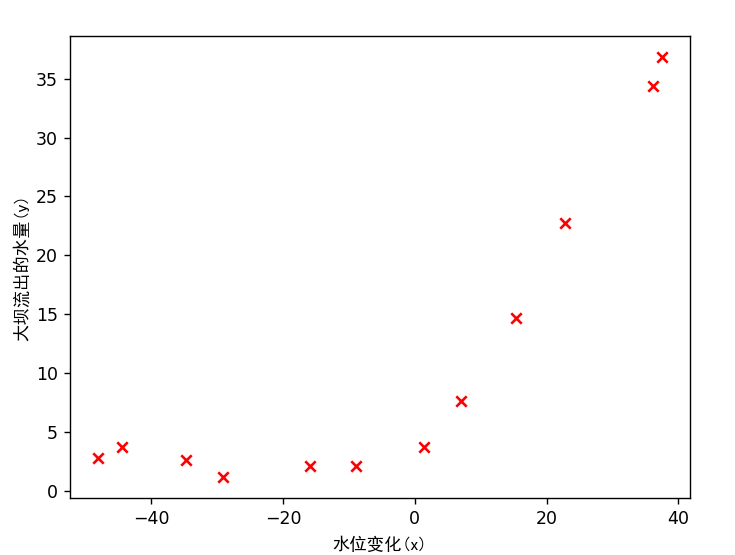
7
# 绘制训练数据
plt.figure()
plt.scatter(X, y, c='r', marker="x")
plt.xlabel('水位变化(x)',fontproperties='SimHei')
plt.ylabel('大坝流出的水量(y)',fontproperties='SimHei')
plt.show()
input('程序暂停。按ENTER键继续')

image-20231122214534375

正则化线性回归

现在应该完善linearRegCostFunction.py文件,实现线性回归功能

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import numpy as np


def linear_reg_cost_function(theta, x, y, lmd):
    # 初始化一些有用的值
    m = y.size

    # 你需要正确返回以下变量
    cost = 0
    grad = np.zeros(theta.shape)

    # 计算误差
    error = x @ theta - y
    
    # 计算正则化项
    reg = lmd * np.sum(np.power(theta[1:], 2))
    
    # 计算代价函数
    cost = (np.sum(error**2) + reg) / (2 * m)
 
    
    # 计算梯度
    grad = (error @ x) / m
    grad[1:] += lmd * theta[1:] / m
    
    return cost, grad

正则化的线性回归在之前的练习中就已经写过，所有可以很顺利的写出

注意：正则化是不包含$\theta_0$的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# ===================== 第 2 部分：正则化线性回归代价 =====================
# 您现在应该实现带正则化的线性回归代价函数。

theta = np.ones(2)
cost, _ = lrcf.linear_reg_cost_function(theta, np.c_[np.ones(m), X], y, 1)

print('theta = [1  1] 时的代价: {:0.6f}\n(该值应约为303.993192)'.format(cost))

input('程序暂停。按ENTER键继续')


# ===================== 第 3 部分：正则化线性回归梯度 =====================
# 您现在应该实现带正则化的线性回归梯度。

theta = np.ones(2)
cost, grad = lrcf.linear_reg_cost_function(theta, np.c_[np.ones(m), X], y, 1)

print('theta = [1  1] 时的梯度: {}\n(该值应约为[-15.303016  598.250744])'.format(grad))

input('程序暂停。按ENTER键继续')

执行测试程序，观察程序的结果是否等于理想的值

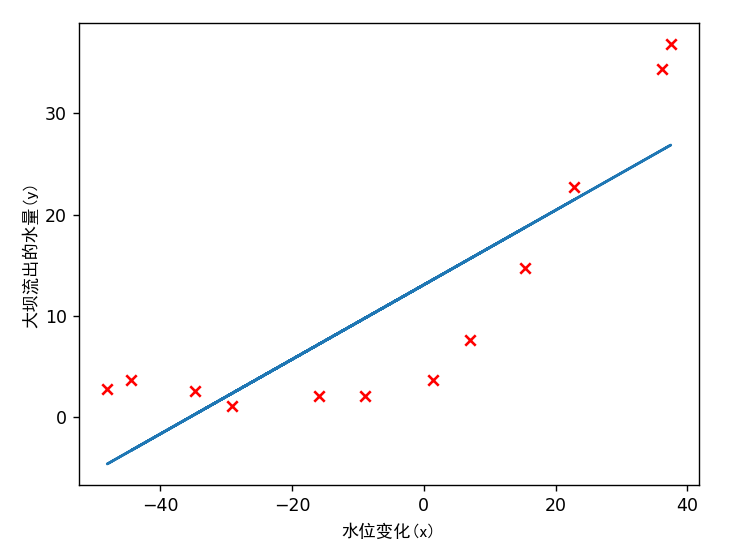
1
2
3
4
5
6
7
8
9
10
11
12
13
# ===================== 第 4 部分：训练线性回归 =====================
# 一旦您正确实现了代价和梯度，train_linear_reg函数将使用您的代价函数来训练正则化线性回归。
#
# 写作说明：数据是非线性的，因此这不会产生很好的拟合。

# 使用 lambda = 0 训练线性回归
lmd = 0

theta = tlr.train_linear_reg(np.c_[np.ones(m), X], y, lmd)

# 在数据上绘制拟合曲线
plt.plot(X, np.dot(np.c_[np.ones(m), X], theta))
input('程序暂停。按ENTER键继续')

画出拟合曲线

image-20231122215513243

学习曲线

完善trainLinearReg.py文件，绘制出学习曲线的图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
import trainLinearReg as tlr
import linearRegCostFunction as lrcf

def learning_curve(X, y, Xval, yval, lmd):
    # 训练样本数
    m = X.shape[0]

    # 需要正确返回这些值
    error_train = np.zeros(m)
    error_val = np.zeros(m)


    for i in range(1, m + 1):
        # 训练子集
        X_subset = X[:i, :]
        y_subset = y[:i]

        # 使用训练子集训练参数
        theta = tlr.train_linear_reg(X_subset, y_subset, lmd)

        # 计算训练误差
        error_train[i - 1], _ = lrcf.linear_reg_cost_function(theta, X_subset, y_subset, 0)

        # 计算交叉验证误差
        error_val[i - 1], _ = lrcf.linear_reg_cost_function(theta, Xval, yval, 0)

    return error_train, error_val

这里使用for循环，逐渐增加训练集和验证集的样本数m，然后把误差存储在error_train和error_val数组中，从而绘制出随着m增加，误差变化的学习曲线

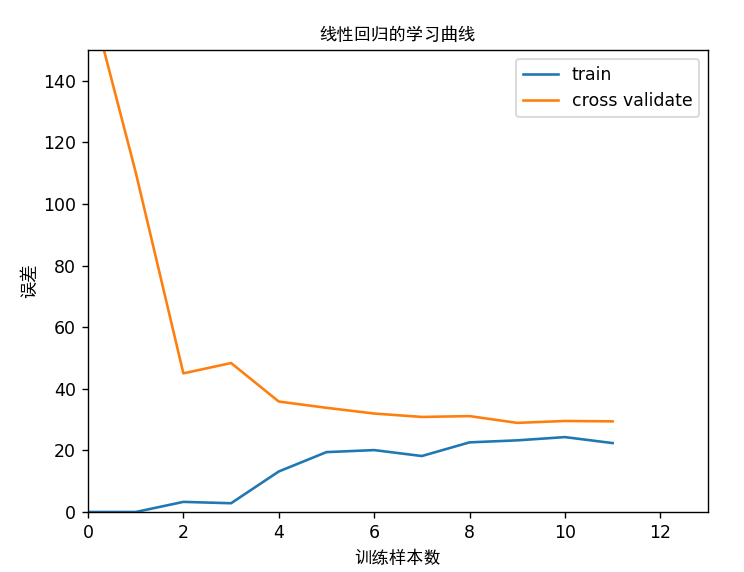
1
2
3
4
5
6
7
8
9
10
11
12
13
lmd = 0
error_train, error_val = lc.learning_curve(np.c_[np.ones(m), X], y, np.c_[np.ones(Xval.shape[0]), Xval], yval, lmd)

plt.figure()
plt.plot(np.arange(m), error_train, np.arange(m), error_val)
plt.title('线性回归的学习曲线',fontproperties='SimHei')
plt.legend(['train', 'cross validate'])
plt.xlabel('训练样本数',fontproperties='SimHei')
plt.ylabel('误差',fontproperties='SimHei')
plt.axis([0, 13, 0, 150])
plt.show()
input('程序暂停。按ENTER键继续')

绘制学习曲线

image-20231122220954572

可以看到，虽然训练样本数的增加，训练集的误差越来越大，最后趋于平缓，而验证集的误差越来越小，最后也趋于平缓

多项式回归的特征映射

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# ===================== 第 6 部分：多项式回归的特征映射 =====================
# 解决这个问题的一种方法是使用多项式回归。您现在应该完成polyFeatures以将每个示例映射到其次数。
p = 5

# 将X映射到多项式特征并进行归一化
# 使用 poly_features 函数将原始特征映射到多项式特征空间
X_poly = pf.poly_features(X, p)
# 对映射后的特征矩阵进行归一化处理
X_poly, mu, sigma = fn.feature_normalize(X_poly)
 # 在特征矩阵左侧添加一列全为 1 的偏置列
X_poly = np.c_[np.ones(m), X_poly]

# 将X_poly_test映射并进行归一化（使用mu和sigma
# 使用相同的映射函数将测试集映射到多项式特征空间）
X_poly_test = pf.poly_features(Xtest, p)
# 使用训练集的均值进行归一化
X_poly_test -= mu  
# 使用训练集的标准差进行归一化
X_poly_test /= sigma
 # 添加偏置列
X_poly_test = np.c_[np.ones(X_poly_test.shape[0]), X_poly_test] 

# 将X_poly_val映射并进行归一化（使用mu和sigma）
# 使用相同的映射函数将交叉验证集映射到多项式特征空间
X_poly_val = pf.poly_features(Xval, p)
# 使用训练集的均值进行归一化
X_poly_val -= mu
# 使用训练集的标准差进行归一化
X_poly_val /= sigma
# 添加偏置列
X_poly_val = np.c_[np.ones(X_poly_val.shape[0]), X_poly_val]  

print('归一化后的训练样本 1 : \n{}'.format(X_poly[0]))

input('程序暂停。按ENTER键继续')

feature_normalize.py是已经给出的python文件，只需要完成polyFeatures即行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np

def poly_features(X, p):
    # 需要正确返回以下变量。
    X_poly = np.zeros((X.size, p))

    # ===================== 在这里填写代码 =====================
    # 说明：给定一个向量 X，返回一个矩阵 X_poly，其中 X_poly 的第 p 列包含 X 的 p 次幂的值。
    #
    for i in range(p):
        X_poly[:, i] = np.power(X, i + 1).flatten()

    # ==========================================================

    return X_poly
"""
假设p=2,那么会输出
[x, y, z
 x²,y²,z²]
"""

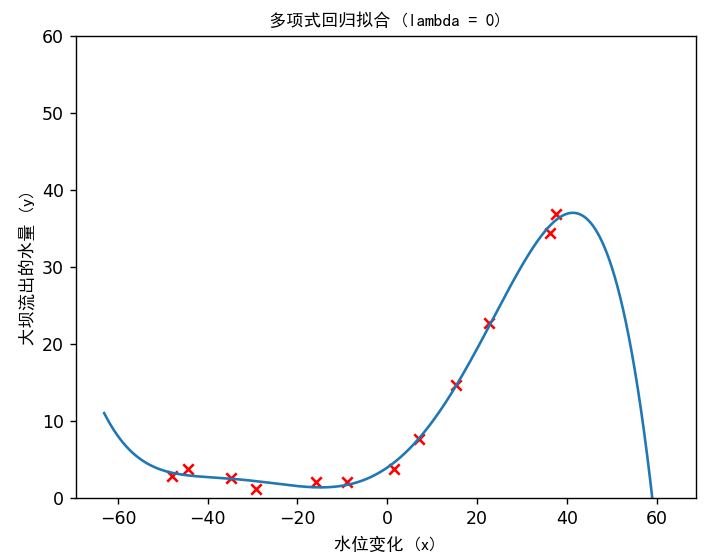
多项式回归的学习曲线

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# ===================== 第 7 部分：多项式回归的学习曲线 =====================
# 现在，您将有机会尝试使用多个lambda值进行多项式回归。
# 下面的代码使用lambda = 0运行多项式回归。您可以尝试使用不同的lambda值运行代码，以查看拟合和学习曲线的变化。

lmd = 0
theta = tlr.train_linear_reg(X_poly, y, lmd)

# 绘制训练数据和拟合曲线
plt.figure()
plt.scatter(X, y, c='r', marker="x")
plotft.plot_fit(np.min(X), np.max(X), mu, sigma, theta, p)
plt.xlabel('水位变化 (x)',fontproperties='SimHei')
plt.ylabel('大坝流出的水量 (y)',fontproperties='SimHei')
plt.ylim([0, 60])
plt.title('多项式回归拟合 (lambda = {})'.format(lmd),fontproperties='SimHei')

train_linear_reg和plot_fit都是已经给出的函数，可以直接调用进行绘图

image-20231123003802275

然后绘制多项式回归的学习曲线

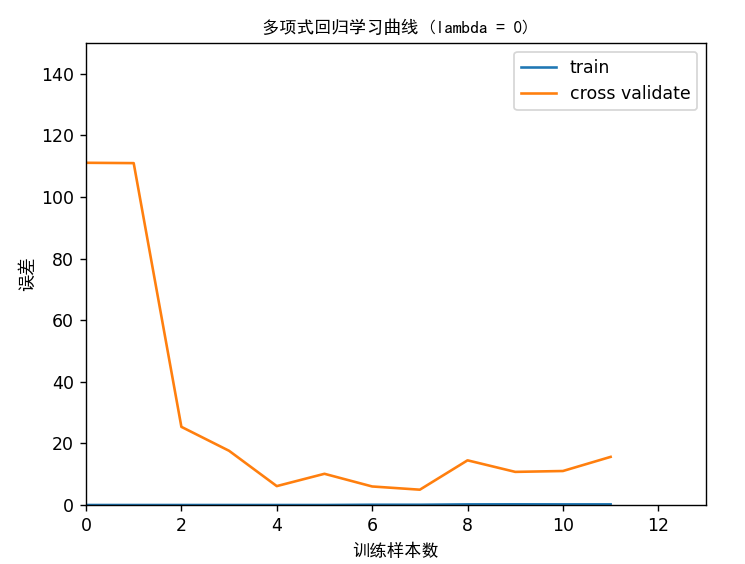
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
error_train, error_val = lc.learning_curve(X_poly, y, X_poly_val, yval, lmd)
plt.figure()
plt.plot(np.arange(m), error_train, np.arange(m), error_val)
plt.title('多项式回归学习曲线 (lambda = {})'.format(lmd),fontproperties='SimHei')
plt.legend(['train', 'cross validate'])
plt.xlabel('训练样本数',fontproperties='SimHei')
plt.ylabel('误差',fontproperties='SimHei')
plt.axis([0, 13, 0, 150])
plt.show()
print('多项式回归 (lambda = {})'.format(lmd))
print('# 训练样本数\t训练误差\t\t交叉验证误差')
for i in range(m):
    print('  \t{}\t\t{}\t{}'.format(i, error_train[i], error_val[i]))

input('程序暂停。按ENTER键继续')

用之前编写的learning_curve函数，计算出error_train, error_val,然后绘制绘图

image-20231123003938758

可以看出，训练集的误差在训练样本不断增大的情况下，误差都很小，而在验证集上，随着训练样本的增大，误差有明显下降，说明训练集存在高方差的问题，即过拟合

测试lambda值

1
2
3
4
5
6
7
8
9
10
11
12
13
# ===================== 第 8 部分：选择Lambda的验证 =====================
# 您现在将实现validationCurve以在验证集上测试各种lambda值。
# 然后，您将使用此值选择“最佳”的lambda值。

lambda_vec, error_train, error_val = vc.validation_curve(X_poly, y, X_poly_val, yval)

plt.figure()
plt.plot(lambda_vec, error_train, lambda_vec, error_val)
plt.legend(['train', 'cross validate'])
plt.xlabel('lambda')
plt.ylabel('误差',fontproperties='SimHei')
plt.show()
input('ex5 完成。按ENTER键退出')

编写validationCurve.py文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
import trainLinearReg as tlr
import linearRegCostFunction as lrcf

def validation_curve(X, y, Xval, yval):
    # 选择的 lambda 值（请勿更改）
    lambda_vec = np.array([0., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10])
    m=len(lambda_vec)
    # 你需要正确返回这些变量。
    error_train = np.zeros(lambda_vec.size)
    error_val = np.zeros(lambda_vec.size)

    # ===================== 你的代码在这里 =====================
    for i in range(m):
        lmd = lambda_vec[i]

        # 使用当前 lambda 训练线性回归模型
        theta = tlr.train_linear_reg(X, y, lmd)

        # 计算训练误差
        error_train[i], _ = lrcf.linear_reg_cost_function(theta, X, y, 0)

        # 计算验证误差
        error_val[i], _ = lrcf.linear_reg_cost_function(theta, Xval, yval, 0)

    # ==========================================================

    return lambda_vec, error_train, error_val

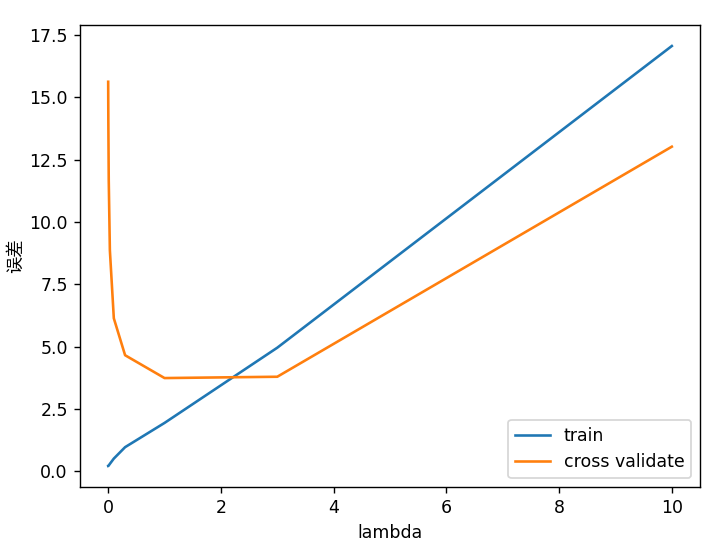
把不同lambda值对应的训练误差和验证误差都求出来，并绘制曲线图

image-20231123010316053

可以看见，随着lambda的增大，验证集的误差先较小后增加，而训练集的误差一直在增加，说明适当的lambda的值降低了过拟合程度，而过大的lambda值让函数欠拟合