应用机器学习的建议

假设环节

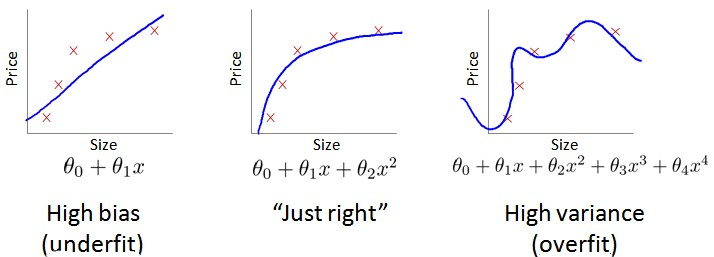
之前已经介绍过了，在机器学习的过程中，会出现过拟合的问题

那么，该如何判断一个假设函数是过拟合的呢？对于这个简单的例子，我们可以对假设函数$h(x)$进行画图，然后观察图形趋势，但对于特征变量不止一个的这种一般情况，还有像有很多特征变量的问题，想要通过画出假设函数来进行观察，就会变得很难甚至是不可能实现。

因此，我们需要另一种方法来评估我们的假设函数过拟合检验。

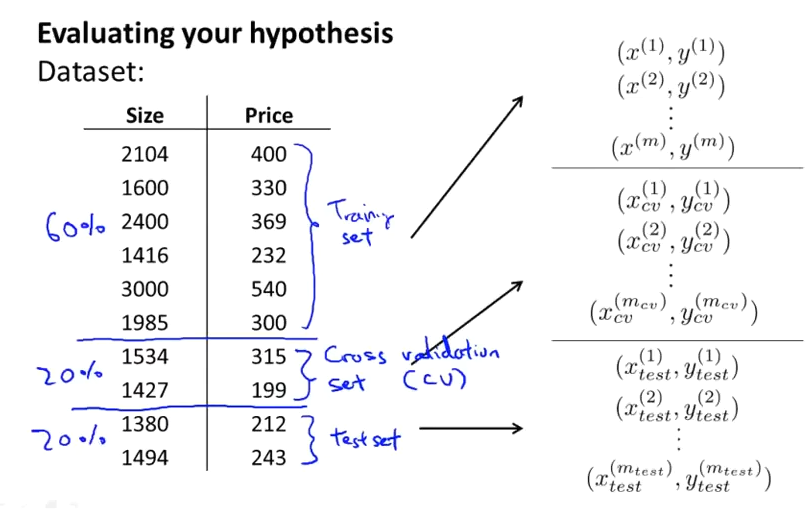
为了检验算法是否过拟合，我们将数据分成训练集和测试集，通常用70%的数据作为训练集，用剩下30%的数据作为测试集。很重要的一点是训练集和测试集均要含有各种类型的数据，通常我们要对数据进行“洗牌”，然后再分成训练集和测试集。

顾名思义，我们在训练集上训练参数theta，然后将theta代入到测试集中观察拟合程度，这样就可以判断是否过拟合

有两种方式计算误差：

对于线性回归模型，我们利用测试集数据计算代价函数$J$
对于逻辑回归模型，可以利用测试数据集来计算代价函数后，在判断预测成功的概率

$J_{test}(\theta) = -\frac{1}{m_{test}}\sum_\limits{i=1}^{m_{test}}\log{h_{\theta}(x^{(i)}_{test})}+(1-{y^{(i)}_{test}})\log{h_{\theta}(x^{(i)}_{test})}$

模型选择

假设有很多二项式模型，比如$h_\theta(x)=\theta_0+\theta_1x$和$h_\theta(x)=\theta_0+\theta_1x+\theta_2x^2…..$

显然越高次数的多项式模型越能够适应我们的训练数据集，但是适应训练数据集并不代表着能推广至一般情况，我们应该选择一个更能适应一般情况的模型。我们需要使用交叉验证集来帮助选择模型。

即：使用60%的数据作为训练集，使用 20%的数据作为交叉验证集，使用20%的数据作为测试集

模型选择的方法为：

使用训练集训练出10个模型
用10个模型分别对交叉验证集计算得出交叉验证误差$J_{cv}(\theta)$（代价函数的值）
选取代价函数值$J_{cv}(\theta)$最小的模型
用步骤3中选出的模型对测试集计算得出推广误差$J_{test}(\theta)$（代价函数的值）

交叉验证集的作用就是辅助选出适合的模型

偏差和方差

当运行一个学习算法时，如果这个算法的表现不理想，那么多半是出现两种情况：

偏差过大：即欠拟合
方差过大：即过拟合

我们在训练模型的时候，肯定需要及时的判断模型是否出现了欠拟合和过拟合的问题，以及如何修改模型，以避免这些问题的出现

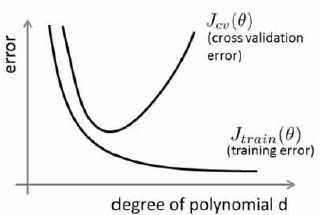
我们通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来帮助分析

首先将横坐标设置拟合函数的次数，将纵轴标设置为代价函数的误差

Training error: $J_{train}(\theta) = \frac{1}{2m}\sum_\limits{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2$

Cross Validation error: $J_{cv}(\theta) = \frac{1}{2m_{cv}}\sum_\limits{i=1}^{m}(h_{\theta}(x^{(i)}_{cv})-y^{(i)}_{cv})^2$

对于训练集，当 $d$ 较小时，模型拟合程度更低，误差较大；随着 $d$ 的增长，拟合程度提高，误差减小。
对于交叉验证集，当 $d$ 较小时，模型拟合程度低，误差较大；但是随着 $d$ 的增长，误差呈现先减小后增大的趋势，转折点是我们的模型开始过拟合训练数据集的时候。

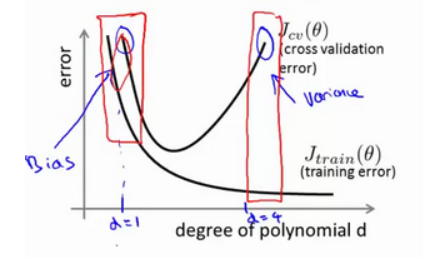
交叉验证集在d较小和d较大的时候，都会出现误差过大的问题：

训练集误差和交叉验证集误差近似时：偏差/欠拟合
交叉验证集误差远大于训练集误差时：方差/过拟合

正则化和偏差/方差

在我们在训练模型的过程中，一般会使用一些正则化方法来防止过拟合。但是我们可能会正则化的程度太高或太小了，即在选择$λ$的值时也需要思考与刚才选择多项式模型次数$d$类似的问题。

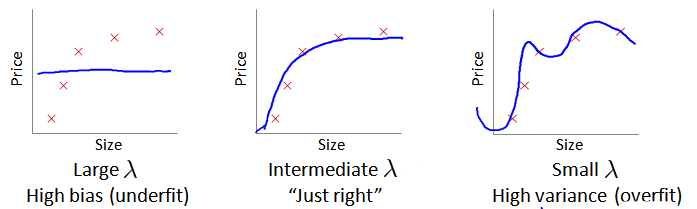
我们选择一系列的想要测试的 $\lambda$ 值，通常是 0-10之间的呈现2倍关系的值（如：$0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10$共12个）。我们同样把数据分为训练集、交叉验证集和测试集。

和选择多项式模型次数d相似，选择$\lambda$的方法为：

使用训练集训练出12个不同程度正则化的模型，得到12个$\theta$
用12个模型分别对交叉验证集计算的出交叉验证误差$J_{train}(\theta)-y$
选择得出交叉验证误差$J_{train}(\theta)-y$最小的模型
运用步骤3中选出模型对测试集计算得出推广误差，我们也可以同时将训练集和交叉验证集模型的代价函数误差与λ的值绘制在一张图表上：

当 $\lambda$ 较小时，训练集误差较小（过拟合）而交叉验证集误差较大\
随着 $\lambda$ 的增加，训练集误差不断增加（欠拟合），而交叉验证集误差则是先减小后增加

学习曲线

使用学习曲线来判断某一个学习算法是否处于偏差、方差问题，学习曲线是学习算法的一个很好的合理检验（sanity check），将训练集误差和交叉验证集误差作为训练集样本数量（$m$）的函数绘制的图表。

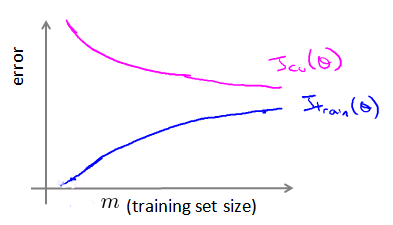
即，如果我们有100行数据，我们从1行数据开始，逐渐学习更多行的数据。思想是：当训练较少行数据的时候，训练的模型将能够非常完美地适应较少的训练数据，但是训练出来的模型却不能很好地适应交叉验证集数据或测试集数据。

所以随着样本数量m的增大，训练集误差是逐渐增加的，而验证集误差在下降，因为得到的模型逐渐拟合

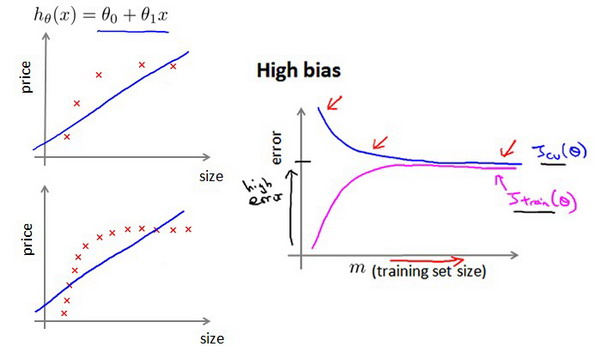
如何利用学习曲线识别高偏差/欠拟合：作为例子，我们尝试用一条直线来适应下面的数据，可以看出，无论训练集有多么大误差都不会有太大改观：

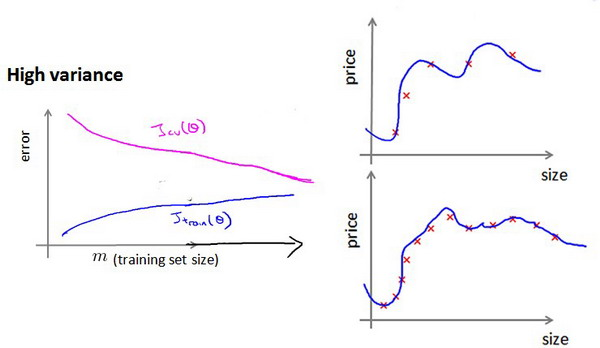
如何利用学习曲线识别高方差/过拟合：假设我们使用一个非常高次的多项式模型，并且正则化非常小，可以看出，当交叉验证集误差远大于训练集误差时，往训练集增加更多数据可以提高模型的效果。

也就是说在高方差/过拟合的情况下，增加更多数据到训练集可能可以提高算法效果。

总结

高偏差(欠拟合)：

尝试获得更多的特征
尝试增加多项式特征
尝试减少正则化程度λ

高方差(过拟合)：

获得更多的训练样本
尝试减少特征的数量
尝试增加正则化程度λ

对于神经网络而言，使用较小的神经网络，类似于参数较少的情况，容易导致高偏差和欠拟合，但计算代价较小使用较大的神经网络，类似于参数较多的情况，容易导致高方差和过拟合，虽然计算代价比较大，但是可以通过正则化手段来调整而更加适应数据。

通常选择较大的神经网络并采用正则化处理会比采用较小的神经网络效果要好。

对于神经网络中的隐藏层的层数的选择，通常从一层开始逐渐增加层数，为了更好地作选择，可以把数据分为训练集、交叉验证集和测试集，针对不同隐藏层层数的神经网络训练神经网络，然后选择交叉验证集代价最小的神经网络。