ex4：Neural Networks Learning

概述

在上一个练习中，您实现了神经网络的前馈传播，并利用我们提供的权重预测了手写数字。在本练习中，您将使用反向传播算法来学习神经网络的参数。

必要的文件如下：

  • ex4.py - python脚本，引导你完成练习
  • ex4data1.mat - 手写数字的训练集
  • ex4weights.mat - 练习4的神经网络参数
  • displayData.py - 用于帮助可视化数据集的函数
  • sigmoid.py - Sigmoid函数
  • computeNumericalGradient.py - 数值计算梯度的函数
  • checkNNGradients.py - 用于检查梯度的函数
  • debugInitializeWeights.py - 用于初始化权重的函数
  • predict.py - 神经网络预测函数

需要完成的文件：

  • sigmoidGradient.py - 计算Sigmoid函数的梯度
  • randInitializeWeights.py - 随机初始化权重
  • nnCostFunction.py- 神经网络成本函数


导入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as scio
import scipy.optimize as opt
import displayData as dd
import nncostfunction as ncf
import sigmoidgradient as sg
import randInitializeWeights as rinit
import checkNNGradients as cng
import predict as pd

# 设置本部分练习中要使用的参数
input_layer_size = 400  # 20x20 的手写数字图像
hidden_layer_size = 25  # 25 个隐藏层单元
num_labels = 10         # 10 个标签，从 0 到 9
                        # 注意我们将 "0" 映射为标签 10


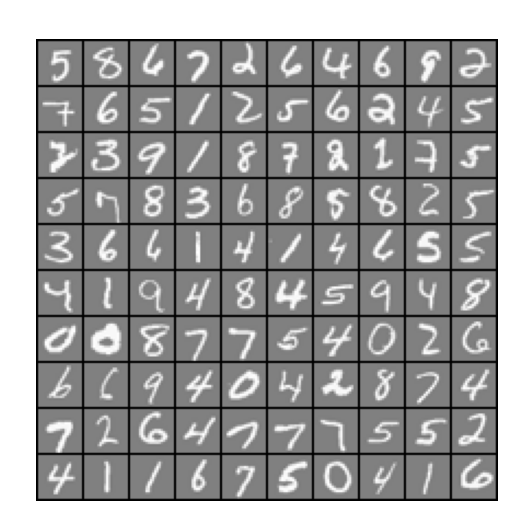
读取和绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# ===================== 第一部分：加载和可视化数据 =====================
# 本部分练习首先通过加载和可视化数据集开始。
# 你将使用一个包含手写数字的数据集。
#

# 加载训练数据
print('加载和可视化数据...')

data = scio.loadmat('ex4data1.mat')
X = data['X']
y = data['y'].flatten()
m = y.size

# 随机选择 100 个数据点进行显示
rand_indices = np.random.permutation(range(m))
selected = X[rand_indices[0:100], :]

dd.display_data(selected)
plt.show()
input('程序暂停。按 ENTER 键继续')

和ex3练习部分一模一样，效果如下：

image-20231119063305322


加载参数

1
2
3
4
5
6
7
8
9
10
# ===================== 第二部分：加载参数 =====================
# 在本部分的练习中，我们加载一些预初始化的神经网络参数

print('加载保存的神经网络参数...')

data = scio.loadmat('ex4weights.mat')
theta1 = data['Theta1']  
theta2 = data['Theta2']

nn_params = np.concatenate([theta1.flatten(), theta2.flatten()])

np.concatenate()是是 NumPy 库中用于连接（拼接）数组的函数。它可以沿指定的轴连接两个或多个数组

这行代码的作用是将两个矩阵 theta1 和 theta2 展平（flatten），然后使用 NumPy 的 concatenate 函数将它们连接成一个一维数组 nn_params。

这种展平和连接的操作是为了在优化算法中更方便地处理参数。


反向传播

前提

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# ===================== 第三部分：计算成本（前向传播） =====================
# 对于神经网络，你应该首先开始实现神经网络的前向传播部分，该部分仅返回成本。你应该完成nncostfunction.py中的代码，以返回成本。
# 在实现前向传播计算成本后，可以通过验证使用固定的调试参数是否得到与我们相同的成本来确认你的实现是否正确。
# 我们建议首先实现不带正则化的前向传播成本，这样你可以更容易进行调试。稍后，在第四部分中，你将实现带正则化的成本。
#

print('使用神经网络进行前向传播...')

# 权重正则化参数（这里我们将其设置为 0）。
lmd = 0

cost, grad = ncf.nn_cost_function(nn_params, input_layer_size, hidden_layer_size, num_labels, X, y, lmd)

print('使用参数（从ex4weights加载）的成本: {:0.6f}\n(这个值应该约为0.287629)'.format(cost))

input('程序暂停。按 ENTER 键继续')


接下来需要完成nncostfunction.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
from sigmoid import *

"""
参数：
    nn_params: 一维数组，包含神经网络的所有参数。
    input_layer_size: 输入层的大小。
    hidden_layer_size: 隐藏层的大小。
    num_labels: 输出层的大小。
    X: 输入数据，大小为(m, input_layer_size)。
    y: 标签，大小为(m,)。
    lmd: 正则化参数。
"""

def nn_cost_function(nn_params, input_layer_size, hidden_layer_size, num_labels, X, y, lmd):
    # 将nn_params重新调整为参数theta1和theta2，即我们两层神经网络的权重2维数组

    theta1 = nn_params[:hidden_layer_size * (input_layer_size + 1)].reshape(hidden_layer_size, input_layer_size + 1)
    theta2 = nn_params[hidden_layer_size * (input_layer_size + 1):].reshape(num_labels, hidden_layer_size + 1)

    
    m = y.size

    #需要返回以下值
    cost = 0
    theta1_grad = np.zeros(theta1.shape)  # 25 x 401
    theta2_grad = np.zeros(theta2.shape)  # 10 x 26


前向传播

根据反向传播的步骤，先进行前向传播

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 第1部分：对神经网络进行前向传播，并将成本存储在变量cost中。
    # 在实现第1部分后，你可以通过运行ex4.py来验证你的成本函数计算是否正确。
    # ===================================================================================

    # 将 X 添加偏置项
    a1 = np.c_[np.ones((m, 1)), X]
    # 计算第一层到第二层的输出
    z2 = np.dot(a1, theta1.T)
    a2 = sigmoid(z2)

    # 在第二层添加偏置项
    a2 = np.c_[np.ones((m, 1)), a2]

    # 计算第二层到输出层的输出
    z3 = np.dot(a2, theta2.T)
    a3 = sigmoid(z3)
    
    #将原始的整数标签 y 转换为独热编码（one-hot encoding）的形式
    y_matrix = np.eye(num_labels)[y - 1]

    # 计算成本（不包含正则化）
    J = np.sum(-y_matrix * np.log(a3) - (1 - y_matrix) * np.log(1 - a3)) / m

代价函数(不含正则)：

这里需要重点关注的是：y_matrix = np.eye(num_labels)[y - 1]

具体来说：

  • np.eye(num_labels) 创建一个大小为 (num_labels, num_labels) 的单位矩阵，其中对角线上的元素为1，其余为0。
  • [y - 1] 使用 y - 1 作为索引，将每个样本的整数标签 y 映射到对应的独热编码向量。

这样，对于每个样本，原始的整数标签被转换为一个长度为 num_labels 的向量，其中只有标签对应的位置为1，其余位置为0。这个独热编码向量可以用于表示样本属于哪个类别。

举一个例子来说明独热编码，如果有3个类别（num_labels = 3）：

  • 原始标签 y = 2 会被转换为独热编码 [0, 1, 0]。
  • 原始标签 y = 1 会被转换为独热编码 [1, 0, 0]。
  • 原始标签 y = 3 会被转换为独热编码 [0, 0, 1]。


在神经网络:表述中，我们提到过，在分类问题中，神经网络的输出结果应该这种形式：

image-20231113064238209

使用独热编码，可以将原本大小为(m,1)大小的y数组，扩展到(m,m)大小，每一行都只在其正确结果未知是’1’,其余为0，让矩阵计算非常方便


反向传播

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 第二部分：实现反向传播算法以计算梯度theta1_grad和theta2_grad。
    # 在theta1_grad和theta2_grad中返回成本函数对theta1和theta2的偏导数。
    # 在实现第二部分后，你可以通过运行checkNNGradients来检查你的实现是否正确。

    # ======================== 反向传播 ========================
    # 计算误差
    delta3 = a3 - y_matrix

    # 计算第二层的误差
    delta2 = np.dot(delta3, theta2) * (a2 * (1 - a2))

    # 去除第二层的偏置项
    delta2 = delta2[:, 1:]

    # 计算梯度
    theta2_grad = np.dot(delta3.T, a2) / m
    theta1_grad = np.dot(delta2.T, a1) / m

首先，先复习一下反向传播的公式：

在代码中，实现起来是比较简单的，

delta3 = a3 - y_matrix：最后一层，即输出层的误差delta，直接用预测值减去真实值可求得

delta2 = np.dot(delta3, theta2) * (a2 * (1 - a2))：隐藏层的误差，用$\Theta^{(2)}\delta^3g’(z^{(2)})$可求而对sigmoid函数求导可知，$$g’(x)=x(1-x)$$代入可得$\delta^{(2)}$

delta2 = delta2[:, 1:]：去掉$\delta^{(2)}$的偏置项，这是因为偏置项不与前一层的激活值相连，所以其误差传播不需要乘以权重，简而言之，偏置的项在$a^1$中根本就找不到对应的激活函数

theta1_grad = np.dot(delta2.T, a1) / m：套用公式计算出$\Theta_1$的梯度,然后除以$m$，这是为了对梯度项取平均。在神经网络的训练中，通常使用 $(m)$ 表示训练样本的数量。这里的目的是确保梯度计算不过于依赖于训练集的规模。


正则化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 第三部分：实现带有成本函数和梯度的正则化。
    # 你可以围绕反向传播的代码来实现这一点。
    # 也就是说，你可以分别计算正则化的梯度，然后将它们添加到第二部分中的theta1_grad和theta2_grad中。
    # ======================== 正则化 ========================
    # 不包含偏置项的参数
    theta1_nobias = theta1[:, 1:]
    theta2_nobias = theta2[:, 1:]

    # 计算正则化项
    regularization = (lmd / (2 * m)) * (np.sum(theta1_nobias ** 2) + np.sum(theta2_nobias ** 2))

    # 加上正则化项的成本
    cost = J + regularization

    # 计算正则化项对梯度的贡献
    theta1_grad[:, 1:] += (lmd / m) * theta1_nobias
    theta2_grad[:, 1:] += (lmd / m) * theta2_nobias

    # 将梯度展开为一维数组
    grad = np.concatenate([theta1_grad.flatten(), theta2_grad.flatten()])


    return cost, grad

正则化的公式为：

注意：这里的i和j都是从1开始，正则化的时候是不含偏置项的

梯度下降的正则化公式如下：

实际上，正如同代码一样，这两步是分开进行的，在反向传播中，最后计算梯度的时候就除以了m

而在正则化中，theta1_grad[:, 1:] += (lmd / m) * theta1_nobias就是对$\Theta$的正则化，这里乘的是$\frac{\lambda}{m}$，而不是公式上的$\lambda$，实际上这是对正则化的缩放，并不违背原理


继续运行ex4.py，查看正则化是否正确

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# ===================== 第四部分：实现正则化 =====================
# 一旦你的成本函数实现正确，现在你应该继续实现带有正则化的成本。
#

print('检查成本函数（带有正则化）...')

# 权重正则化参数（这里我们将其设置为 1）。
lmd = 1

cost, grad = ncf.nn_cost_function(nn_params, input_layer_size, hidden_layer_size, num_labels, X, y, lmd)

print('使用参数（从ex4weights加载）的成本: {:0.6f}\n(这个值应该约为0.383770)'.format(cost))

input('程序暂停。按 ENTER 键继续')

调用写好的nn_cost_function.py，观察结果是否正确


Sigmoid梯度

1
2
3
4
5
6
7
8
9
10
11
# ===================== 第五部分：Sigmoid梯度 =====================
# 在开始实现神经网络之前，你将首先实现 sigmoid 函数的梯度。你应该完成 sigmoidGradient.py 文件中的代码
#

print('评估 sigmoid 梯度...')

g = sg.sigmoid_gradient(np.array([-1, -0.5, 0, 0.5, 1]))

print('在 [-1  -0.5  0  0.5  1] 处评估的 sigmoid 梯度:\n{}'.format(g))

input('程序暂停。按 ENTER 键继续')

编写sigmoid_gradient.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def sigmoid_gradient(z):
    g = np.zeros(z.shape)

    # 说明：计算 z 中每个值的 sigmoid 函数梯度。
    # 可以使用已导入的 sigmoid 函数。

    # 计算 sigmoid 函数的值
    s = sigmoid(z)
    
    # 计算梯度
    g = s * (1 - s)

    # ===========================================================

    return g

很简单，已知$g’(x)=x*(1-x)$,代码表示出来即可

初始化参数

1
2
3
4
5
6
7
8
9
10
11
# ===================== 第六部分：初始化参数 =====================
# 在本部分的练习中，你将开始实现一个能够对数字进行分类的两层神经网络。你将从实现一个初始化神经网络权重的函数（randInitializeWeights.m）开始。
#

print('初始化神经网络参数...')

initial_theta1 = rinit.rand_initialization(input_layer_size, hidden_layer_size)
initial_theta2 = rinit.rand_initialization(hidden_layer_size, num_labels)

# 展开参数
initial_nn_params = np.concatenate([initial_theta1.flatten(), initial_theta2.flatten()])

需要我们编写rand_initialization.py，以实现theta矩阵的初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np

def rand_initialization(l_in, l_out):
    # 创建一个初始权重矩阵，包含偏置单元的参数
    w = np.zeros((l_out, 1 + l_in))

    # 说明：随机初始化 w，打破神经网络训练中的对称性。
    # 注意：w 的第一列对应于偏置单元的参数。

    # 使用 np.uniform 随机初始化权重，范围在[-epsilon, epsilon]之间
    epsilon_init = 0.12
    w = np.random.uniform(-epsilon_init, epsilon_init, size=(l_out, 1 + l_in))

    # ===========================================================

    return w

训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# ===================== 第七部分：训练NN =====================
# 你现在已经实现了训练神经网络所需的所有代码。要训练你的神经网络，我们现在将使用 'opt.fmin_cg'。
#

print('训练神经网络... ')

lmd = 1

def cost_func(p):
    return ncf.nn_cost_function(p, input_layer_size, hidden_layer_size, num_labels, X, y, lmd)[0]

def grad_func(p):
    return ncf.nn_cost_function(p, input_layer_size, hidden_layer_size, num_labels, X, y, lmd)[1]

nn_params, *unused = opt.fmin_cg(cost_func, fprime=grad_func, x0=nn_params, disp=True, full_output=True)

# 从 nn_params 中恢复 theta1 和 theta2
theta1 = nn_params[:hidden_layer_size * (input_layer_size + 1)].reshape(hidden_layer_size, input_layer_size + 1)
theta2 = nn_params[hidden_layer_size * (input_layer_size + 1):].reshape(num_labels, hidden_layer_size + 1)

input('程序暂停。按 ENTER 键继续')

可视化权重

1
2
3
4
5
6
7
8
9
# ===================== 第十部分：可视化权重 =====================
# 你现在可以通过显示隐藏单元来“可视化”神经网络正在学习什么特征，以查看神经网络学到了什么样的数据特征

print('可视化神经网络...')

dd.display_data(theta1[:, 1:])
plt.show()
input('程序暂停。按 ENTER 键继续')

是一副模糊的图像：

image-20231119083857840

预测

1
2
3
4
5
6
7
8
# ===================== 第十一部分：实现预测 =====================
# 在训练完神经网络后，我们想要使用它来预测标签。现在你将实现 'predict' 函数，使用神经网络预测训练集的标签。这让你计算训练集准确性。

pred = pd.predict(theta1, theta2, X)

print('训练集准确性: {}'.format(np.mean(pred == y)*100))

input('ex4 完成。按 ENTER 键退出')

训练集准确性: 99.7