神经网络：学习

代价函数

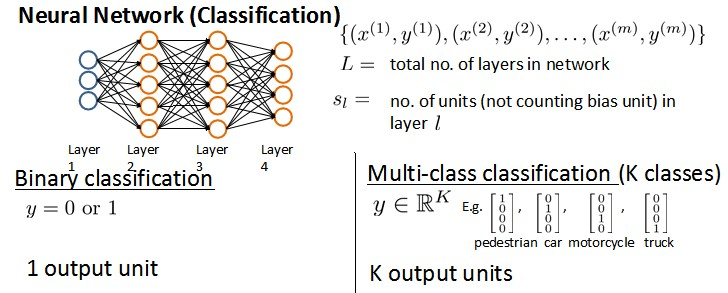
假设神经网络的训练样本有$m$个，每个包含一组输入$x$和一组输出信号$y$，$L$表示神经网络层数，$S_I$表示每层的神经元个数($S_l$表示在$l$层的神经元个数)，$S_L$代表最后一层中处理单元的个数。

将神经网络的分类定义为两种情况：二类分类和多类分类，

二类分类：$S_L=1, y=0\, or\, 1$表示哪一类；

$K$类分类：$S_L=k, y_i = 1$表示分到第$i$类；$(k>2)$

回顾逻辑回归问题中的代价函数：

$J\left(\theta \right)=-\frac{1}{m}\left[\sum_\limits{i=1}^{m}{y}^{(i)}\log{h_\theta({x}^{(i)})}+\left(1-{y}^{(i)}\right)log\left(1-h_\theta\left({x}^{(i)}\right)\right)\right]+\frac{\lambda}{2m}\sum_\limits{j=1}^{n}{\theta_j}^{2}$

在逻辑回归中，我们只有一个输出变量，也只有一个因变量$y$，但是在神经网络中，我们可以有很多输出变量

而在神经网络中，输出层可以有多个输出，假设输出层的神经元数量为K，神经网络的代价函数如下：

$J(\Theta) = -\frac{1}{m} \sum\limits_{i=1}^{m} \sum\limits_{k=1}^{K} y_k^{(i)} \log \left(h_\Theta(x^{(i)})_k\right) + \left(1 - y_k^{(i)}\right) \log \left(1 - h_\Theta(x^{(i)})_k\right) + \frac{\lambda}{2m} \sum\limits_{l=1}^{L-1} \sum\limits_{i=1}^{s_l} \sum\limits_{j=1}^{s_{l+1}} \left(\Theta_{ji}^{(l)}\right)^2$

$m$ 是训练样本的数量。
$(y_k^{(i)})$ 是样本 $(i)$ 对于类别 $(k)$ 的实际标签。
$(\hat{y}_k^{(i)})$ 是模型对样本 $(i)$ 对于类别 $(k)$ 的预测。
$(\Theta^{(l)})$ 是第 $(l)$ 层到第 $(l+1)$ 层的权重矩阵。
$L$ 是神经网络的层数。
$s_l$ 是第 $(l)$ 层的神经元数量。
$\lambda$是正则化参数。

这个看起来复杂很多的代价函数背后的思想还是一样的，我们希望通过代价函数来观察算法预测的结果与真实情况的误差有多大，最后的代价函数是要计算所有输出层的代价

唯一不同的是，对于每一行特征，我们都会给出$K$个预测，基本上我们可以利用循环，对每一行特征都预测$K$个不同结果，然后在利用循环在$K$个预测中选择可能性最高的一个，将其与$y$中的实际数据进行比较。

反向传播算法

之前我们在计算神经网络预测结果的时候我们采用了一种正向传播方法，我们从第一层开始正向一层一层进行计算，直到最后一层的$h_{\theta}\left(x\right)$

在上一个实验：6.5 ex3：Multi-class Classifification and Neural Networks中，就使用了正向传播方法，很轻松的识别出了手写数字，在ex3中，权重矩阵$\theta$是已经被训练好的，实验的时候只需要调用就行，但是，在实际应用中，权重矩阵的参数我们显然是需要自己进行训练的，这就引出了反向传播算法

BP（反向传播）的主要目的是通过调整神经网络的权重和偏差，使网络在训练数据上的预测更接近实际标签，从而最小化代价函数。代价函数是衡量网络输出与实际标签之间差异的指标，BP通过梯度下降的方式降低这个差异。

既然BP是通过梯度下降来降低这个差异，那么需要先求代价函数$J(\Theta)$的偏导数$\frac{\partial}{\partial\Theta^{(l)}_{ij}}J\left(\Theta\right)$

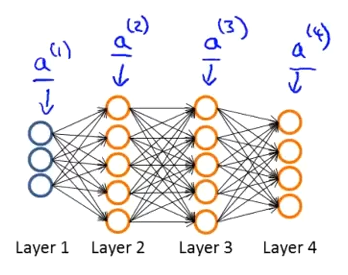
举例来说明反向传播算法：假设我们的训练集只有一个样本$\left({x}^{(1)},{y}^{(1)}\right)$，我们的神经网络是一个四层的神经网络，如图：

随机初始化

任何优化算法都需要一些初始的参数。到目前为止我们都是初始所有参数为0，这样的初始方法对于逻辑回归来说是可行的，但是对于神经网络来说是不可行的。如果我们令所有的初始参数都为0，这将意味着我们第二层的所有激活单元都会有相同的值。同理，如果我们初始所有的参数都为一个非0的数，结果也是一样的。

我们通常假设初始参数为正负$ε$之间的随机值，假设我们要随机初始一个尺寸为10×11的参数矩阵，代码如下：

1 2	epsilon = 0.01 theta = np.random.uniform(low=-epsilon, high=epsilon, size=(10, 11))

前向传播

先用前向传播算法算出代价$J(\Theta)$：

神经网络的正向传播计算如下：

输入层（第1层）：
$[ a^{(1)} = x^{(1)} ]$
隐藏层1（第2层）：
$[ z^{(2)} = \Theta^{(1)}a^{(1)} ]$
$[ a^{(2)} = g(z^{(2)}) ]$

其中，$(g)$ 是激活函数，$(\Theta^{(1)})$ 是连接输入层和隐藏层1的权重矩阵。
隐藏层2（第3层）：
$[ z^{(3)} = \Theta^{(2)}a^{(2)} ]$
$[ a^{(3)} = g(z^{(3)}) ]$

其中，$(\Theta^{(2)})$ 是连接隐藏层1和隐藏层2的权重矩阵。
输出层（第4层）：
$[ z^{(4)} = \Theta^{(3)}a^{(3)} ]$
$[ a^{(4)} = h_\Theta(x^{(1)}) = g(z^{(4)}) ]$

其中，$(\Theta^{(3)})$ 是连接隐藏层2和输出层的权重矩阵，$(h_\Theta(x^{(1)}))$ 是神经网络的输出。

反向传播

接下来，使用反向传播算法，首先，我们定义误差项为

$\delta^{(L)} = \frac{\partial J}{\partial z^{(L)}}$

其中$z^{(L)}$是输出层的净输入。通过链式法则，我们可以将$\delta^{(L)}$传播到前一层，形成对每个参数的偏导数。这样，我们可以使用梯度下降等优化算法来调整网络参数，以最小化损失函数

而输出层的误差显然是：$\delta^{(4)}=a^{(4)}-y$

证明如下：

首先，我们有输出层的激活值 $(a^{(4)})$ 和损失函数 $(J)$ 之间的关系。在分类问题中，常用的损失函数是交叉熵损失函数。假设我们的网络是针对二分类问题，输出层使用 $sigmoid$ 激活函数，那么交叉熵损失函数可以表示为：

$J(y, a^{(4)}) = - y \log(a^{(4)}) - (1 - y) \log(1 - a^{(4)})$

其中，$(y)$ 是实际标签（0或1），$a^{(4)}$ 是输出层的激活值。

接下来，我们来计算输出层激活值 $(a^{(4)})$ 对净输入值 $(z^{(4)})$ 的偏导数。假设输出层使用 $sigmoid$ 激活函数，有 $(a^{(4)}) = g(z^{(4)}))$，其中 $(g(\cdot))$ 是 $sigmoid$ 函数。$sigmoid$ 函数的导数可以表示为

$(g'(z^{(4)}) = a^{(4)} \cdot (1 - a^{(4)}))。$

应用链式法则：

$\frac{\partial J}{\partial z^{(4)}} = \frac{\partial J}{\partial a^{(4)}} \cdot \frac{\partial a^{(4)}}{\partial z^{(4)}}$

将损失函数对激活值的偏导数代入：

$\frac{\partial J}{\partial z^{(4)}} = -(\frac{y}{a^{(4)}} - \frac{(1-y)}{(1-a^{(4)})}) \cdot a^{(4)} \cdot (1 - a^{(4)})$

化简上式：

$\frac{\partial J}{\partial z^{(4)}} = a^{(4)} - y$

这个结果表示了输出层误差项与实际标签之间的差异，与损失函数对于输出层净输入值的偏导数是一致的。

然后计算上一层的误差项 ($\delta^{(3)}$)：

$\delta^{(3)} = \frac{\partial J}{\partial z^{(3)}}$

使用链式法则，将 $(\frac{\partial J}{\partial z^{(3)}})$ 分解为两部分：

$\frac{\partial J}{\partial z^{(3)}} = \frac{\partial J}{\partial a^{(3)}} \cdot \frac{\partial a^{(3)}}{\partial z^{(3)}}$

考虑激活函数的导数：

$\frac{\partial a^{(3)}}{\partial z^{(3)}} = g'\left(z^{(3)}\right)$

将上述结果代入步骤2：

$\delta^{(3)} = \frac{\partial J}{\partial a^{(3)}} \cdot g'\left(z^{(3)}\right)$

重点是计算$\frac{\partial J}{\partial a^{(3)}}$项：推论如下：

根据链式法则，有：

$\frac{\partial J}{\partial a^{(3)}} = \frac{\partial J}{\partial z^{(4)}} \cdot \frac{\partial z^{(4)}}{\partial a^{(3)}}$

其中，$(z^{(4)})$ 是输出层的净输入值，而 $(a^{(3)})$ 是输出层的激活值。

我们知道 $\frac{\partial J}{\partial z^{(4)}} = \delta^{(4)}$，根据之前的讨论。接下来，我们需要计算 ($\frac{\partial z^{(4)}}{\partial a^{(3)}}$)，在一般的神经网络中，输出层的净输入值 ($z^{(4)}$) 与前一层的激活值 ($a^{(3)}$) 之间有以下关系：

$z^{(4)} = \Theta^{(3)} \cdot a^{(3)}$

其中，$(\Theta^{(3)})$ 是连接输出层和前一隐藏层的权重矩阵。对上式关于 $(a^{(3)})$ 求偏导数，得到：

$\frac{\partial z^{(4)}}{\partial a^{(3)}} = \Theta^{(3)}$

现在，将这两个结果代入链式法则的表达式：

$\frac{\partial J}{\partial a^{(3)}} = \delta^{(4)} \cdot \left(\Theta^{(3)}\right)^T$

这就得到了

$\frac{\partial J}{\partial a^{(3)}} = \left(\Theta^{(3)}\right)^T \cdot \delta^{(4)}$

这个结果表明，损失函数对于前一层的激活值的偏导数可以通过将输出层误差项与权重矩阵的转置相乘得到。这是误差反向传播算法中计算梯度的一部分

代入上述结果：

$\delta^{(3)} = \left(\Theta^{(3)}\right)^T \cdot \delta^{(4)} \cdot g'\left(z^{(3)}\right)$

计算梯度

通过上述方法可以算出所有误差的表达式：

$\delta^{(2)}=(\Theta^{(2)})^{T}\delta^{(3)}\ast g'(z^{(2)})$

$\delta^{(1)}=0$ 因为输入层是输入变量，不存在误差，我们有了所有的误差的表达式后，便可以计算权重矩阵的梯度

权重矩阵梯度的具体推导：

假设我们有一个神经网络，其中 $(a^{(l)})$ 是第 $(l)$ 层的激活值（包括输入层），$(\Theta^{(l)})$ 是连接第 $(l)$ 层和第 $(l+1)$ 层的权重矩阵，$(\delta^{(l+1)})$ 是第 $(l+1)$ 层的误差项。

激活值和净输入的关系为：$(a^{(l+1)} = g(z^{(l+1)}))$

其中$，(g(\cdot))$ 是激活函数，$(z^{(l+1)})$ 是第 $(l+1)$ 层的净输入

我们知道误差项的定义是：

$\delta^{(l+1)} = \frac{\partial J}{\partial z^{(l+1)}}$

现在，我们来计算损失函数对于第 $(l)$ 层的权重矩阵 $(\Theta^{(l)})$ 的偏导数，即梯度。使用链式法则：

$\frac{\partial J}{\partial \Theta^{(l)}} = \frac{\partial J}{\partial z^{(l+1)}} \cdot \frac{\partial z^{(l+1)}}{\partial \Theta^{(l)}}$

我们知道 $(\frac{\partial J}{\partial z^{(l+1)}} = \delta^{(l+1)})$，然后考虑 $(z^{(l+1)})$ 与权重矩阵的关系：

$z^{(l+1)} = \Theta^{(l)} \cdot a^{(l)}$

对上式对 $(\Theta^{(l)})$ 求偏导数得到：

$\frac{\partial z^{(l+1)}}{\partial \Theta^{(l)}} = a^{(l)}$

现在，将上述结果代入梯度计算的表达式：

$\frac{\partial J}{\partial \Theta^{(l)}} = \delta^{(l+1)} \cdot \frac{\partial z^{(l+1)}}{\partial \Theta^{(l)}} = \delta^{(l+1)} \cdot a^{(l)T}$

最终，我们得到了权重矩阵的梯度计算公式：

$\frac{\partial J}{\partial \Theta^{(l)}} = \delta^{(l+1)} \cdot a^{(l)T}$

对于偏置的梯度：

$\frac{\partial J}{\partial \Theta^{(l)}} = \delta^{(l+1)}$

这个公式表示了损失函数对于第 $(l)$ 层权重矩阵的偏导数，是反向传播算法中梯度计算的关键步骤之一。

梯度下降

首先将梯度简写为$\Delta_{ij}^{(l)}$，第 $l$ 层的第 $i$ 个激活单元受到第 $j$ 个参数影响而导致的误差。

$\frac{\partial J}{\partial \Theta^{(l)}} = \delta^{(l+1)}_i \cdot a^{(l)T}_j=\Delta^{(l)}$

换句话说，$(\delta^{(l+1)} \cdot a^{(l)T})$ 是一个矩阵，其中第 $(i)$ 行、第 $(j)$ 列的元素就是 $(\Delta_{ij}^{(l)})$。这个矩阵表示了损失函数对于权重矩阵的梯度，用于更新权重以减小损失。

在求出了$\Delta_{ij}^{(l)}$之后，我们便可以计算代价函数的偏导数了，计算方法如下：

$ D_{ij}^{(l)} :=\frac{1}{m}\Delta_{ij}^{(l)}+\lambda\Theta_{ij}^{(l)}$ ${if}\; j \neq 0$

$ D_{ij}^{(l)} :=\frac{1}{m}\Delta_{ij}^{(l)}$ ${if}\; j = 0$

在神经网络的训练中，我们通过梯度下降算法来不断调整网络中的权重，使得网络的输出更接近实际值。为了防止过拟合，通常在损失函数中加入正则化项。

这里的公式是在计算正则化项的梯度，用于更新权重时的调整。让我们逐步解释：

$\Delta_{ij}^{(l)}:$ 这是神经网络中权重矩阵 $\Theta^{(l)}$的梯度项。它表示损失函数对于权重的影响，是梯度下降算法的关键。
$\frac{1}{m}$:
$\lambda$: 这是正则化参数，它控制正则化项的强度。如果 $(\lambda)$ 较大，那么正则化的影响就会更显著。
$\Theta_{ij}^{(l)}$: 这是权重矩阵中的具体权重值。

现在，整个公式的含义是，我们通过将权重的梯度项取平均，然后加上正则化项，来计算最终用于更新权重的梯度。这个过程旨在防止过拟合，通过对权重的大小进行调整，以使模型更一般化

梯度检验

我们对一个较为复杂的模型（例如神经网络）使用梯度下降算法时，可能会存在一些不容易察觉的错误，意味着，虽然代价看上去在不断减小，但最终的结果可能并不是最优解。

为了避免这样的问题，我们采取一种叫做梯度的数值检验（Numerical Gradient Checking）方法。这种方法的思想是通过估计梯度值来检验我们计算的导数值是否真的是我们要求的。

对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。即对于某个特定的 $\theta$，我们计算出在 $\theta$-$\varepsilon $ 处和 $\theta$+$\varepsilon $ 的代价值（$\varepsilon $是一个非常小的值，通常选取 0.001），然后求两个代价的平均，用以估计在 $\theta$ 处的代价值。

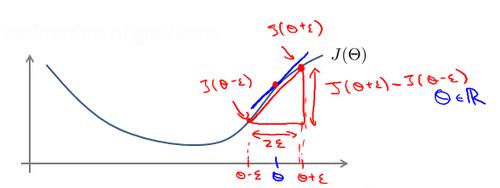
梯度检验是一种验证数值计算中梯度计算是否正确的技术。在机器学习中，特别是在神经网络训练中，梯度是优化算法（如梯度下降）的关键部分。通过梯度检验，可以验证你的梯度计算是否正确，以确保你的模型在学习过程中能够正确地更新参数。

计算数值梯度： 对于每个参数 $(\theta_i)$，通过微小的变化 $(\epsilon)$ 来计算数值梯度。数值梯度的计算方式是：
$\text{num-grad}_i = \frac{J(\theta_1, \theta_2, ..., \theta_i + \epsilon, ..., \theta_n) - J(\theta_1, \theta_2, ..., \theta_i - \epsilon, ..., \theta_n)}{2\epsilon}$
其中，$(J)$ 是损失函数，$(\theta_i)$ 是第 $(i)$ 个参数。
计算反向传播梯度： 使用反向传播算法计算损失函数对于每个参数的梯度。
比较： 将数值梯度与反向传播梯度进行比较。如果两者非常接近，那么可以认为梯度计算是正确的。

梯度检验是一种相对慢速但非常强大的调试工具。在实际应用中，梯度检验通常只在开发和调试阶段使用，因为它相对于反向传播来说计算量较大，不适合在大规模数据上进行频繁的计算。当然，梯度检验也有一些局限性，例如对于非连续、非凸或计算复杂的损失函数可能不太适用。

总结

反向传播（Backpropagation，简称BP）是一种用于训练神经网络的优化算法。以下是反向传播算法包含的主要步骤：

初始化参数： 随机初始化神经网络的权重和偏置。
正向传播： 使用当前的参数进行正向传播，计算网络的输出。每一层的激活值 $(a^{(l)} )$ 可以通过应用激活函数到该层的净输入值 $(z^{(l)} )$ 而得到。
$z^{(l)} = \Theta^{(l-1)} a^{(l-1)} + b^{(l-1)}$ $a^{(l)} = g(z^{(l)})$
其中， $(\Theta^{(l-1)} )$ 是连接第 $(l-1 )$ 层和第 $(l )$ 层的权重矩阵， $(b^{(l-1)} )$ 是偏置。
计算损失： 使用网络的输出和实际标签计算损失函数。
$J = \text{cost}(a^{(L)}, y)$
其中， $(L )$ 是输出层的索引， $(a^{(L)} )$ 是输出层的激活值， $(y )$ 是实际标签。
反向传播： 通过反向传播算法计算每一层的误差项 ($\delta^{(l)}$ )。误差项的计算方式取决于激活函数的选择和损失函数的形式。
$\delta^{(L)} = \frac{\partial J}{\partial z^{(L)}}$ $\delta^{(l)} = \left(\Theta^{(l)}\right)^T \delta^{(l+1)} \ast g'\left(z^{(l)}\right)$

计算梯度： 利用误差项 $(\delta^{(l)} )$ 计算损失函数对于参数的偏导数，即梯度。
$\frac{\partial J}{\partial \Theta^{(l)}} = a^{(l-1)} \cdot \delta^{(l)T}$
正则化梯度：
$D_{ij}^{(l)} :=\frac{1}{m}\Delta_{ij}^{(l)}+\lambda\Theta_{ij}^{(l)}$
梯度下降更新参数： 使用梯度下降或其他优化算法，根据计算得到的梯度更新网络的参数。
$\Theta^{(l)} = \Theta^{(l)} - \alpha \frac{\partial J}{\partial \Theta^{(l)}}$
其中， $(\alpha )$ 是学习率，用于控制更新步长。
重复： 重复步骤 2-7，直到损失函数收敛或达到预定的迭代次数。

这些步骤组成了反向传播算法的基本流程，用于训练神经网络。反向传播通过不断地调整网络参数，使得模型逐渐学到数据中的模式，从而提高模型的性能。