ex3：Multi-class Classifification and Neural Networks

逻辑回归

概述

在本练习中，您将使用逻辑回归和神经网络来识别手写数字(从0到9)。如今，手写数字的自动识别已得到广泛应用-从识别邮件信封上的邮政编码(邮政编码)到识别银行支票上的金额。本练习将向您展示如何将所学方法用于这项分类任务。

在练习的第一部分，您将扩展之前的逻辑回归实施方法，并将其应用于”单对全”分类。

必要的文件如下：

  • ex3.py-引导您完成练习的Python文件
  • ex3data1.mat -前半部分练习的数据集
  • sigmoid.py-计算$sigmoid$函数
  • displayData.py-展示图像

需要完成的文件：

  • predictOneVsAll.py- 使用一对所有多类别分类器进行预测

  • oneVsAll.py - 训练一对所有多类别分类器

  • lrCostFunction.py-$logistic$回归成本函数


导入

1
2
3
4
5
6
7
import matplotlib.pyplot as plt   
import numpy as np
import scipy.io as scio   
import lrCostFunction as lCF  
import oneVsAll as ova
import predictOneVsAll as pova
import displayData as dd

loadmat函数是SciPy库中scipy.io模块中的一个函数，用于加载MATLAB文件（.mat）中的数据。它允许你读取MATLAB文件中的变量，并将其存储在Python字典中。以下是关于loadmat函数的一些重要信息：

scipy.io.loadmat(file_name, mdict=None, appendmat=True, **kwargs)

  • file_name: 字符串，表示MATLAB文件的路径。
  • mdict: 可选参数，如果提供了一个字典，MATLAB文件中的变量将被存储在这个字典中。
  • appendmat: 可选参数，如果为True（默认值），则MATLAB文件的.mat扩展名将被附加到file_name中，如果没有的话。
  • **kwargs: 其他可选参数，可以用于控制MATLAB文件加载的行为。

loadmat函数返回一个字典，其中包含MATLAB文件中的所有变量。字典的键是MATLAB变量的名称，而相应的值是包含变量数据的NumPy数组或其他适当的Python对象。


读取

1
2
3
4
5
6
7
8
9
10

# 设置本部分练习所需的参数
input_layer_size = 400  # 输入层大小，即20x20像素的手写数字图像
num_labels = 10         # 类别数量，从0到9
                        # 注意我们将数字 "0" 映射到类别编号 10      
    
data = scio.loadmat('ex3data1.mat')   #用loadmat载入数据
X = data['X']  
y = data['y'].flatten()
m = y.size

数据集ex3data1.mat包含了5000个训练示例，每个示例都是一个20x20像素的数字灰度图像。每个像素由一个浮点数表示，代表该位置的灰度强度。为了进行机器学习模型的训练，这些图像被展开成了一个400维的向量。

因此，数据矩阵X是一个大小为5000x400 的矩阵，其中每一行都代表一个手写数字图像的训练示例。

而矩阵y是一个大小为5000的一维向量，是数字1到10之间的整数，表示有10种类别，对应于每个训练示例代表的手写数字(0,9)，类别10对应的数字0，原来是应该是5000x1的矩阵，flatten之后就变为了1维向量

简单来说，每个训练示例都是一个20x20的图像，被展开成一个包含400个元素的向量。这样的表示方式使得图像可以作为机器学习算法的输入。每个元素对应于图像中的一个像素，其值表示该像素的灰度强度。


绘图

1
2
3
4
5
6
# Randomly select 100 data points to display
rand_indices = np.random.permutation(range(m))
selected = X[rand_indices[0:100], :]

dd.display_data(selected)
plt.show()

这段代码的作用是从训练集 X 中随机选择100个数据点，并将它们展示出来，display_data.py是初始时自带的，不需要我们编写,只需要调用即可

np.random.permutation(range(m)) ：生成一个包含0到m-1的随机排列，其中 m 是训练集中样本的数量

rand_indices[0:100] ：选择排列的前100个索引，即从0到99

图像如下：

image-20231115055129570


梯度下降

编写lrCostFunction.py文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import numpy as np
from sigmoid import *


def lr_cost_function(theta, X, y, lmd):
    parameters = theta.shape[0]

    # 初始化grad数组来存储每个参数的梯度
    grad = np.zeros(parameters)

    pos = y @ np.log(sigmoid(X @ theta))  # 代价函数的前半段
    # 添加小常数，代价函数的后半段
    neg = (1 - y) @ np.log(1 - sigmoid(X @ theta) + 1e-15)
    reg = (lmd / (2 * len(X))) * np.sum(np.power(theta[1:], 2))

    cost = ((-np.sum(pos + neg))) / (len(X)) + reg  # 算出代价

    return cost


def gradient(theta, X, y, learning_rate):
    m = len(y)
    h = sigmoid(X @ theta)
    grad = (1 / m) * (X.T @ (h - y))
    grad[1:] += (learning_rate / m) * theta[1:]
    return grad

函数的内容和ex2练习中的正则化函数完全相同，具体解释请参见ex2:logistic regression，这里只是算出了第一次梯度下降的梯度，作为后面高级优化的参数


分类器

编写oneVsAll.py，要求实现多类别逻辑回归的训练，具体来说，使用一对多（one-vs-all）的方法来训练多个二元逻辑回归分类器，每个分类器用于预测一个类别是否为正例。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import lrCostFunction as lcf
from sigmoid import *
from scipy.optimize import minimize


def one_vs_all(X, y, num_labels, learning_rate):
    #m,n分别是X的行和列的数目,实际上是(5000,400)
    m, n = X.shape
    #创建一个矩阵 all_theta，用于存储每个类别的权重参数,算上偏置项，大小为(10,401)
    all_theta = np.zeros((num_labels, n + 1))

    # 在 X 前添加一列，表示偏置项
    X = np.c_[np.ones((m, 1)), X]

    for i in range(1, num_labels + 1):
            # 将标签转换为二元标签，表示当前类别和其他类别
            binary_labels = np.array([1 if item == i else 0 for item in y])

            # 初始化权重，大小为401
            initial_theta = np.zeros(n + 1)

            # 使用梯度下降来训练分类器
            result = minimize(lcf.lr_cost_function, initial_theta, args=(X, binary_labels, learning_rate), method='BFGS',jac=lcf.gradient)

            # 将训练好的权重存储在结果矩阵中
            all_theta[i - 1, :] = result.x

    return all_theta





详细解释一下：

  • np.c_()是numpy的连接函数，表示连接括号里面的数组或矩阵，这里，np.ones((m, 1)) 创建了一个列向量，所有元素都是 1，表示偏置项。然后，np.c_ 将这列向量与特征矩阵 X 进行按列连接，形成一个新的特征矩阵，其中第一列是全 1 的列。

    所以，最终的 X 矩阵包含了原始特征矩阵 X 的所有列，并在最左侧添加了一列偏置项。这是逻辑回归中常见的预处理步骤，以便更好地进行模型训练。此时X矩阵的大小为(5000,401)

  • binary_labels = np.array([1 if item == i else 0 for item in y]):这是一个列表推导式，它遍历 y 中的每个元素 item，然后根据条件 item == i 返回 1 或 0，作用如下

    1
    2
    3
    4
    5
    6
    7
    """
    假设此时i=6
    操作前：    操作后
    [1,2,3    [0,0,0
     4,5,6     0,0,1 
     7,8,9]    0,0,0]
    """


    经过分类后，变成了简单的二元分类的逻辑回归问题，在每次循环中的大小和y的大小一致，为(10,401)

  • initial_theta = np.zeros(n + 1)：用于存储每个类别的权重参数。每一行对应一个类别，每一列对应一个特征（包括偏置项）

  • result = minimize(lcf.lr_cost_function, initial_theta, args=(X, binary_labels, learning_rate), method='BFGS',jac=lcf.gradient)这行代码使用 BFGS 算法最小化目标函数 lcf.lr_cost_function

    • lcf.lr_cost_function：这是目标函数，即要最小化的函数
    • initial_theta：是优化过程的初始猜测值
    • args=(X, binary_labels, learning_rate)：这是一个元组，包含传递给目标函数 lcf.lr_cost_function 的额外参数。在这里，包括特征矩阵 X、二元标签 binary_labels 和学习率 learning_rate
    • method='BFGS'：这是选择优化算法的参数。在这里，选择了 BFGS 算法
    • jac=lcf.gradient：这是目标函数的梯度函数。在这里，lcf.gradient 是计算逻辑回归代价函数梯度的函数。提供梯度信息可以加速优化过程
    • 最终，minimize 函数返回一个对象 result，其中包含有关优化结果的信息，如最小化的目标值、最小值对应的参数等。result是一个可以通过 result.x 获取最小化目标函数时的参数值矩阵，里面就是最优的theta矩阵，其大小和initial_theta一样

  • all_theta[i - 1, :] = result.x，将将针对当前类别 i 训练得到的权重参数存储在 all_theta 矩阵的相应行中，result.x的大小为401，最后的all_theta矩阵的大小为(10,401)，每一行对应每个数组的权重参数


回到ex3.py中来，调用分类器

1
2
lmd = 0.1   #学习率为0.1
all_theta = ova.one_vs_all(X, y, num_labels, lmd)

得到all_theta，一个大小为(10,401)的权重矩阵


预测

编写predictOneVsAll.py，对结果进行预测

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
from sigmoid  import *

# all_theta:包含每个类别的权重参数的矩阵,大小为(10,401)
# X:待预测的样本特征矩阵，大小为(5000,400)

def predict_one_vs_all(all_theta, X):
   # 样本数量
    m = X.shape[0]

    # 初始化预测向量
    p = np.zeros(m)

    # 在 X 前添加一列，表示偏置项
    X = np.c_[np.ones(m), X]

    # 使用学习到的权重进行预测
    predictions = sigmoid(X @ all_theta.T)

    # 选择每一行中最大值的索引，即预测的类别
    p = (np.argmax(predictions, axis=1))  # 加1是因为 Python 中索引是从0开始的，而类别是从1开始的

    return p


  • predictions = sigmoid(X @ all_theta.T),因为X@all_theta.T会产生一个(5000,10)的矩阵,经过sigmoid变换之后，每一行的内容，就是该图像为某数字的概率的集合，假设第1行，第3列为0.64，说明第1个图像，为数字3的概率为0.64，即64%

  • p = (np.argmax(predictions, axis=1) + 1) ：np.argmax 函数返回沿指定轴（在这里是轴1，即每行）的最大值的索引。即直接找出，每一行最大的值，所对应的列是什么

    对于 predictions 矩阵，这将返回每个样本对应的预测概率最大的类别的索引。由于类别编号是从 1 开始的，所以将上一步得到的索引值加上 1，最后每一行的值为概率最大的值所在的列再加1，返回的p最后的大小为(5000,)


回到ex3.py中

1
2
pred = pova.predict_one_vs_all(all_theta, X)
print('Training set accuracy: {}'.format(np.mean(pred == y)*100))

调用predict_one_vs_all函数，得到了pred数组，然后直接和正确答案y对比，得到最后的准确率，准确率应该是96.43%


神经网络

概述

在本练习的前一部分，您实施了多类逻辑回归来识别手写数字。然而,逻辑回归不能形成更复杂的假设，因为它只是一种线性分类器。

在这部分练习中，您将使用与之前相同的训练集，建立一个神经网络来识别手写数字。神经网络将能够表示形成非线性推理的复杂模型。您将使用我们已经训练过的神经网络的参数。你们的目标是实现前馈传播算法，使用我们的权重进行预测。

必要的文件如下：

ex3_nn.py-引导您完成练习的Python文件

ex3data1.mat -练习的数据集

ex3weights.mat-神经网络练习的初始权重

sigmoid.py-计算$sigmoid$函数

displayData.py-展示图像


需要完成的文件：

  • predict.py-神经网络预测函数


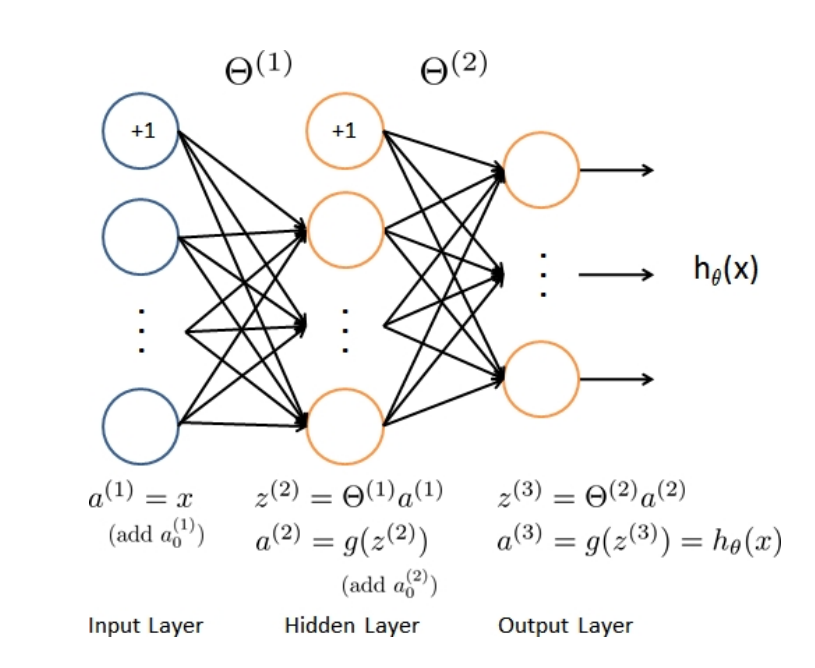
神经网络如图2所示。它有3层—输入层、隐藏层和输出层。回想一下，我们的输入是数字图像的像素值。由于图像大小为20×20,因此我们有400个输入层单元(不包括额外的偏置单元，该单元总是输出+1)。与之前一样， 训练数据将被加载到变量X和y中。

我们为您提供了一组已经训练过的网络参数$\theta_1,\theta_2$。这些参数存储在ex3weights.mat中，并将由ex3_nn.py加载到Theta1和Theta2中。参数的尺寸适合第二层有25个单元和10个输出单元(对应10个数字类别)的神经网络。

image-20231116020346330


导入并绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as scio

import displayData as dd
import predict as pd


# 设置本部分练习所需的参数
input_layer_size = 400  # 输入层大小，即20x20像素的手写数字图像
hidden_layer_size = 25  # 隐藏层大小，包含25个神经元
num_labels = 10         # 类别数量，从0到9
                        # 注意我们将数字 "0" 映射到类别编号 10



# Load Training Data
print('Loading and Visualizing Data ...')

data = scio.loadmat('ex3data1.mat')
X = data['X']
y = data['y'].flatten()
m = y.size

# Randomly select 100 data points to display
rand_indices = np.random.permutation(range(m))
selected = X[rand_indices[0:100], :]

dd.display_data(selected)
plt.show()
input('Program paused. Press ENTER to continue')

和逻辑回归的写法一致


预测

载入已经训练好的权重矩阵theta1和theta2

1
2
3
data = scio.loadmat('ex3weights.mat')
theta1 = data['Theta1']
theta2 = data['Theta2']

最主要的是编写predict.py，返回神经网络的预测结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import numpy as np
from sigmoid import *

def predict(theta1, theta2, X):
    """
    使用训练好的神经网络参数进行预测。

    Parameters:
    - theta1: numpy array,大小为(25,401)
      第一层的权重参数。
    - theta2: numpy array,大小为(10,26)
      第二层的权重参数。
    - X: numpy array,大小为(5000,400)
      待预测的样本特征矩阵。每行对应一个样本，每列对应一个特征。

    Returns:
    - p: numpy array
      包含每个样本预测的类别的一维数组。类别编号从1开始。
    """
    # 增加偏置项
    m = X.shape[0]
    X = np.c_[np.ones((m, 1)), X]

    # 计算第一层到第二层的激活值
    a1 = X
    z2 = a1 @ theta1.T
    a2 = sigmoid(z2)

    # 在 a2 前添加偏置项
    a2 = np.c_[np.ones((m, 1)), a2]

    # 计算第二层到输出层的激活值
    z3 = a2 @ theta2.T
    a3 = sigmoid(z3)

    # 选择每一行中最大值的索引，即预测的类别
    p = np.argmax(a3, axis=1) + 1  # 加1是因为 Python 中索引是从0开始的，而类别是从1开始的

    return p


回到ex3_nn.py中调用predict

1
2
3
4
pred = pd.predict(theta1, theta2, X)

print('Training set accuracy: {}'.format(np.mean(pred == y)*100))

结果应该是97.52%