6.0.神经网络:表述
神经网络:表述
非线性假设
无论是线性回归还是逻辑回归都有这样一个缺点,即:当特征太多时,计算的负荷会非常大
比如像下图中的分类问题:
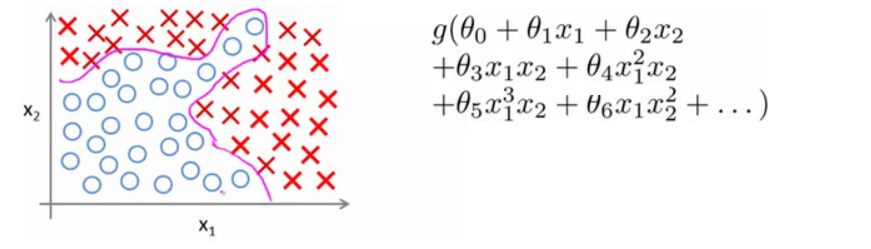
假设我们有非常多的特征,例如大于100个变量,我们希望用这100个特征来构建一个非线性的多项式模型,结果将是数量非常惊人的特征组合
即便我们只采用两两特征的组合$(x_1x_2+x_1x_3+x_1x_4+…+x_2x_3+x_2x_4+…+x_{99}x_{100})$,我们也会有接近5000个组合而成的特征。这对于一般的逻辑回归来说需要计算的特征太多了。
普通的逻辑回归模型,不能有效地处理这么多的特征,这时候我们需要神经网络
模型表示
神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型。这些神经元(也叫激活单元)采纳一些特征作为输出,并且根据本身的模型提供一个输出
下图是一个以逻辑回归模型作为自身学习模型的神经元示例,在神经网络中,参数又可被成为权重(weight)
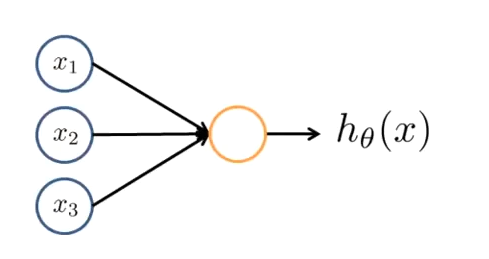
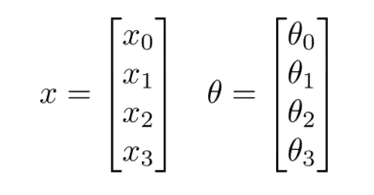
以下是神经元的主要功能和组成部分:
输入(Input): 神经元接收来自其他神经元或外部环境的输入。这些输入通常是由权重加权的特征值。图中的$x_1,x_2,x_3$就是输入
权重(Weight): 每个输入都有一个相关的权重$\theta_1,\theta_2,\theta_3$。这些权重表示每个特征对神经元输出的影响程度。
偏置(Bias): 除了输入和权重之外,神经元还有一个偏置项$x_0$,它对输出的影响独立于输入。而$\theta_0$是偏执项的权重
激活函数(Activation Function): 逻辑回归使用逻辑函数(也称为Sigmoid函数),将输入的加权和与偏置相加,并将结果压缩到(0, 1)的范围内。
输出(Output): 神经元的最终输出是通过激活函数处理后的结果。这个输出将作为下一层神经元的输入或是整个神经网络的最终输出,具体取决于神经网络的结构和任务。在逻辑回归模型中,输出为:$h_\theta\left( x \right)=\frac{1}{1+{e^{-\theta^TX }}}$
神经网络模型是许多逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。Layer 1 成为输入层(Input Layer),Layer 2 成为隐藏层(Hidden Layers),Layer 3称为输出层(Output Layer)。为每一层都增加一个偏差单位(bias unit):
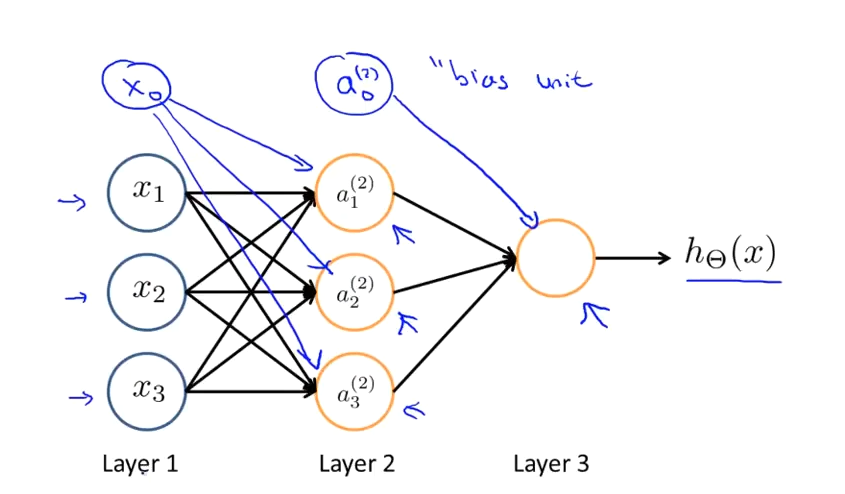
其中$x_1$, $x_2$, $x_3$是输入单元,我们将原始数据输入给它们。$a_1$, $a_2$, $a_3$是中间单元,它们负责将数据进行处理,然后呈递到下一层。最后是输出单元,它负责计算${h_\theta}\left( x \right)$
下面引入一些标记法来帮助描述模型:
$a_{i}^{\left( j \right)}$ 代表第$j$ 层的第 $i$ 个激活单元。
${\theta ^{\left( j \right)}}$代表从第 $j$ 层映射到第$ j+1$ 层时的权重矩阵,其尺寸为:以第 $j+1$层的激活单元数量为行数,以第 $j$ 层的激活单元数加一为列数的矩阵。即为$(n_{j+1} \times (n_j+1))$大小
- 权重矩阵$\theta^{(1)}$的维度将是 ($n_{\text{2}} \times (n_{\text{1}} + 1)$)。即为$3\times 4$的矩阵,这里加一是因为通常会在输入中添加一个偏置项(bias),用于调整隐藏层节点的阈值。
- 权重矩阵$\theta^{(2)}$的维度是 ($n_{\text{3}} \times (n_{\text{2}} + 1)$)。即为$1\times 4$的矩阵大小
权重矩阵的行,是取决于$j+1$层的激活单元数量$n_{j+1}$,这是因为权重矩阵的每一行对应于连接到下一层的一个激活单元(神经元)。权重矩阵$\begin{bmatrix}
\theta_{1n} \\
\theta_{2n}\\
\theta_{3n}\\
…
\end{bmatrix}
$的每一行都会和输入的特征矩阵$[x_1,x_2,x_3…]$做点积,从而形成新的激活单元
权重矩阵的列,是取决于$j$层的激活单元数量$n_j+1$,这是因为,列的数量,直接对应的是每一行权重的数量,之所以要加1,因为要加上偏置$x_0=1$,自然每一行就多了一个权重$\theta_0$要计算
一定要多联想之前学过的回归知识,线性回归和逻辑回归的时候,都会插入为数值’1’的列作为$x_0$,最后的theta数组也都是从$\theta_0$开始的
对于上图所示的模型,激活单元和输出分别表达为:
$a_{1}^{(2)}=g(\Theta _{10}^{(1)}x_{0}+\Theta _{11}^{(1)}x_{1}+\Theta _{12}^{(1)}x_{2}+\Theta _{13}^{(1)}x_{3})$
$a_{2}^{(2)}=g(\Theta _{20}^{(1)}x_{0}+\Theta _{21}^{(1)}x_{1}+\Theta _{22}^{(1)}x_{2}+\Theta _{23}^{(1)}x_{3})$
$a_{3}^{(2)}=g(\Theta _{30}^{(1)}x_{0}+\Theta _{31}^{(1)}x_{1}+\Theta _{32}^{(1)}x_{2}+\Theta _{33}^{(1)}x_{3})$
$h_{\Theta}(x)=g(\Theta _{10}^{(2)}a_{0}^{(2)}+\Theta _{11}^{(2)}a_{1}^{(2)}+\Theta _{12}^{(2)}a_{2}^{(2)}+\Theta _{13}^{(2)}a_{3}^{(2)})$
为了更好了了解Neuron Networks的工作原理,先把例子左半部分遮住:
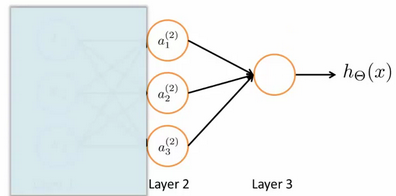
右半部分其实就是以$a_0, a_1, a_2, a_3$, 按照逻辑回归的方式输出$h_\theta(x)$:
其中,$g(x)$就是sigmoid函数,只不过我们把逻辑回归中的输入向量$\left[ x_1\sim {x_3} \right]$ 变成了中间层的$\left[ a_1^{(2)}\sim a_3^{(2)} \right]$, 即: $h_{\Theta}(x)=g(\Theta _{10}^{(2)}a_{0}^{(2)}+\Theta _{11}^{(2)}a_{1}^{(2)}+\Theta _{12}^{(2)}a_{2}^{(2)}+\Theta _{13}^{(2)}a_{3}^{(2)})$
我们可以把$a_0, a_1, a_2, a_3$看成更为高级的特征值,也就是$x_0, x_1, x_2, x_3$的进化体,并且它们是由 $x$与$\theta$决定的,因为是梯度下降的,所以$a$是变化的,并且变得越来越厉害,所以这些更高级的特征值远比仅仅将 $x^3$之类的多项式作为特征值厉害,也能更好的预测新数据。
这就是神经网络相比于逻辑回归和线性回归的优势。
这里需要重点说明一下,和线性回归最大的区别在于,线性回归可以我们清晰的知道,每一个$\theta$所对应的特征是什么,比如$\theta_1$是拟合$x_1$的,$\theta_2$是拟合$x_2^2$的
但是在神经网络中,通常无法直接解释每一个权重对应的具体含义,比如$\theta_1$是$3\times 4$的矩阵,一共有12个权重$\theta_{ij}$,我们根本不知道每一个权重所影响特征多项式具体是什么,就算$a_{1}^{(2)}$和$a_{2}^{(2)}$的输入特征虽然是一样的,但是其权重是未知的,所以结果也不会一样,这也是深度学习模型被称为“黑箱模型”的一个原因
把$x$, $\theta$, $a$ 分别用矩阵表示
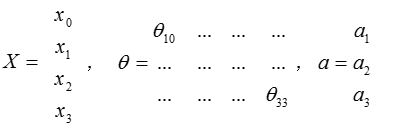
可以得到$\theta \cdot X=a$ ,把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION )
多类分类
当我们有不止两种分类时(也就是$y=1,2,3….$),比如以下这种情况,该怎么办?如果我们要训练一个神经网络算法来识别路人、汽车、摩托车和卡车,在输出层我们应该有4个值。例如,第一个值为1或0用于预测是否是行人,第二个值用于判断是否为汽车。
输入向量$x$有三个维度,两个中间层,输出层4个神经元分别用来表示4类,也就是每一个数据在输出层都会出现${\left[ a\text{ }b\text{ }c\text{ }d \right]^{T}}$,且$a,b,c,d$中仅有一个为1,表示当前类。下面是该神经网络的可能结构示例:
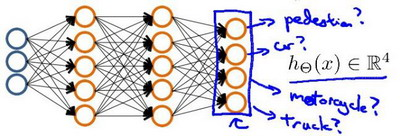
神经网络算法的输出结果为四种可能情形之一:



