ex2:logistic regression

概述

在这部分练习中，您将建立一个逻辑回归模型来预测学生是否被大学录取。

假设您是一所大学的管理者，您想根据两次考试的成绩来确定每位申请人的录取几率。您有以前申请者的历史数据，可以用作逻辑回归的训练集。对于每个训练示例，您都有申请人的两次考试成绩和录取决定。

您的任务是建立一个分类模型，根据这两次考试的分数估算申请人的录取概率。

必要的文件如下：

  • ex2.py-引导您完成练习的Python文件

  • ex2data1.txt -前半部分练习的数据集

需要完成的部分：

  • sigmoid.py-计算$sigmoid$函数
  • costFunction.py-$logistic$回归成本函数
  • predict.py-逻辑回归预测函数


导入

1
2
3
4
5
6
7
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.optimize as opt
import costFunction as cf
import predict as predict
from sigmoid import

SciPy（Scientific Python）是一个用于科学计算的库，而 scipy.optimize 模块则提供了各种优化算法。


读取并绘图

1
data=pd.read_csv('ex2data1.txt',header=None,names=['exam1','exam2','label'])

原始数据有3列，分别是命名为exam1列，exam2列和label列，label列的数据是0或者1

1
2
pos = data[data['label'] == 1]
neg = data[data['label'] == 0]

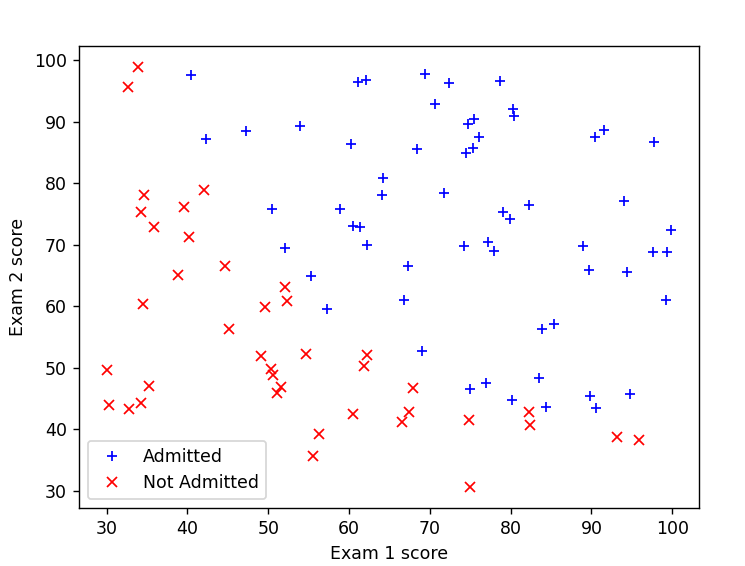
绘图的难点在于要根据label值，绘制不同形状的散点，Pandas的对象可以直接根据布尔值来进行提取，通过判断label值，就可以将data数据根据label分为pos和neg两堆

1
2
3
4
5
6
7
8
9
10
# 对于正类别
plt.plot(pos['exam1'], pos['exam2'], 'b+', label='Admitted')

# 对于负类别
plt.plot(neg['exam1'], neg['exam2'], 'rx', label='Not Admitted')

plt.xlabel('Exam 1 score')
plt.ylabel('Exam 2 score')
plt.legend()
plt.show()

通过plot函数分别画出pos和neg的图像

image-20231110223001509


梯度下降

1
data.insert(0,'ones',1)

依旧是先在第一列插入0，作为$x_0$列

1
2
3
4
col=data.shape[1]  #col就是data的列
X = data.iloc[:, 0:col-1]
y = data.iloc[:, col-1]
initial_theta = np.zeros(X.shape[1])

初始化theta数组，X数据由data的前3列构成，y则由最后一列构成


接下来需要编写sigmoid.py，实现sigmoid函数的计算

1
2
3
4
5
6
import numpy as np

def sigmoid(z):
    g = 1/(1+np.exp(-z))
    return g

np.exp() 是 NumPy 库中的指数函数，用于计算给定输入数组的每个元素的指数值


然后编写costFunction.py文件，用于计算起始时的代价cost和梯度grad

将$h_\theta x$用sigmoid函数计算出来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from sigmoid import *

def cost_function(theta, X, y):
     pos = y@np.log(sigmoid(X @ theta))    #代价函数的前半段
     # 添加小常数，代价函数的后半段
     neg = (1 - y)@np.log(1 - sigmoid(X@theta) + 1e-15) 
     cost= -np.sum(pos + neg) / (len(X))    #算出代价
       
     return cost

def gradient(theta, X, y):
    #获取参数数量  
    m=len(y)
    
    #初始化grad数组来存储每个参数的梯度
    grad = np.zeros(m)
    
    # 计算模型预测与实际标签之间的误差
    error = sigmoid(X @ theta) - y
    
    grad = (1 / m) * (X.T @ error)  # 计算梯度

    return grad

在计算neg的时候，为了避免log函数里面出现0，添加了1e-15这个极小常数

这里并没有更新grad，因为只需要算出初始化的梯度就行了


1
2
3
4
cost = cf.cost_function(initial_theta, X, y)
grad=  cf.gradient(initial_theta, X, y)
print(f'Cost at initial theta (zeros): {cost}')
print(f'Gradient at initial theta (zeros):{grad}')

在ex2.py中调用函数求出cost和grad并打印出来,结果符合预期


高级优化

接下来，使用scipy库中的opt.fmin_bfgs函数，来实现梯度下降中的bfgs算法

1
2
3
4
5
6
7
8
9
def cost_func(t):
    return cf.cost_function(t, X, y)

theta, cost, *unused = opt.fmin_bfgs(f=cost_func, x0=initial_theta,full_output=True)

print(cost)
print('Expected cost (approx): 0.203')
print(theta)
print('Expected Theta (approx): \n-25.161\n0.206\n0.201')

在代码中，cost_func 和 grad_func 都接受一个参数 t，该参数是一个包含所有优化变量的数组。这种形式的好处是可以满足 scipy.optimize.fmin_bfgs 函数对目标函数和梯度函数的单参数要求。

这里没有提供fprime，函数使用近似值，仍然可以得到正确答案

最后将最优参数赋值给 theta，最优值赋值给 cost。 *unused 部分用于接收 opt.fmin_bfgs 返回的其他信息，但在这里我们没有使用它。


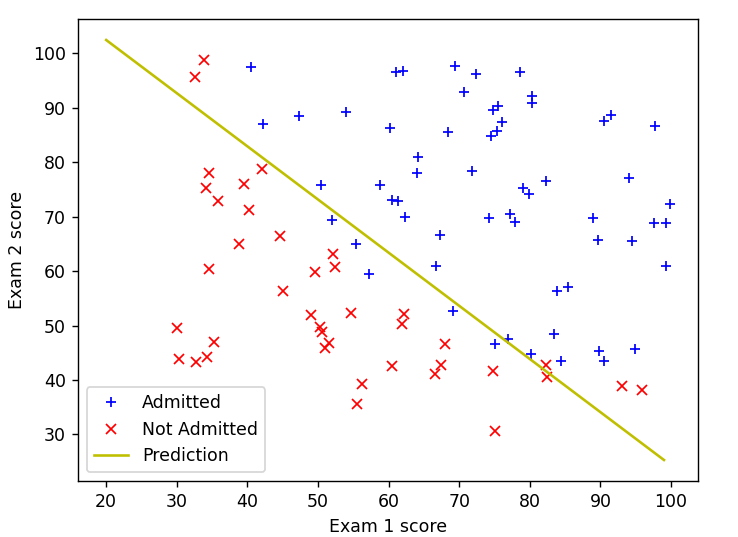
最后利用得到的最优参数theta绘制回归曲线

1
2
3
4
5
6
7
8
9
10
11
# 从20到100，步长为1
plotting_x1 = np.arange(20,100,1)

# x1和x2，要把其中一个看成是y
plotting_h1 = ( - theta[0] - theta[1] * plotting_x1) / theta[2]


plt.plot(plotting_x1, plotting_h1, 'y', label='Prediction')
plt.legend()

plt.show()


在逻辑回归中，决策边界是由模型的预测结果决定的，而模型的预测结果通过 sigmoid 函数进行变换，使其落在 (0, 1) 之间。因此，决策边界在逻辑回归中实际上是 sigmoid 函数的输出为 0.5 的地方。

对于线性决策边界，它满足以下条件：

在这个公式中，($x_1$) 和 ($x_2$) 是特征，($\theta_0, \theta_1, \theta_2$) 是模型的参数。这个线性方程的解决方案就是决策边界。

如果我们将上面的方程表示为 ($x_2 = f(x_1)$)，那么就可以使用上面的代码来画出这个线性决策边界。这里，我们通过解这个线性方程来表示决策边界。

对于 sigmoid 函数的决策边界，确实是通过设置 ($sigmoid(\theta^T \cdot X) = 0.5$) 来获得，但这是在参数空间（$\theta$） 空间中，而不是特征空间（($x$) 空间）中

image-20231111020607578

预测一下exam1为45分，exam为85分的录取概率

1
2
3
4
prob = sigmoid(np.array([1, 45, 85])@(theta))
print('For a student with scores 45 and 85, we predict an admission probability of {prob}')
print('Expected value : 0.775 +/- 0.002')

结果为0.776，即有77.6%的概率被录取


最后检测一下通过参数$\theta$预测的准确度，首先编写predict.py

1
2
3
4
5
def predict(theta, X):
    m = X.shape[0]

    probability = sigmoid(X @ theta.T)
    return [1 if x >= 0.5 else 0 for x in probability]

逻辑很简单，如果算出来的probability大于等于0.5，那么就直接返回1，如果小于0.5，返回0

在ex2.py中调用predict.py中的predict函数

1
2
3
4
p = predict.predict(theta, X)

print(f'Train accuracy: {np.mean(y == p) * 100}')
print('Expected accuracy (approx): 89.0')

np.mean(y == p) * 100: 计算预测准确度。这里通过 y == p 创建一个布尔数组，表示每个样本的真实标签是否与预测标签相等。np.mean 函数会把True看做是1，计算这个布尔数组中 True 的比例，即正确预测的样本占总样本的比例。乘以 100 就得到了准确度的百分比。


正则化

正则化的逻辑回归的代价函数为：

正则化的梯度下降的公式为：

所以只需要在costFunciton.py文件的基础上，将正则项加入运算即可

代价函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def cost_function_reg(theta, X, y, lmd):
    #获取训练样本的数量
    m = len(y)   

    # 初始化grad数组来存储每个参数的梯度
    grad = np.zeros(m)
    pos = y @ np.log(sigmoid(X @ theta))  # 代价函数的前半段
    # 添加小常数，代价函数的后半段
    neg = (1 - y) @ np.log(1 - sigmoid(X @ theta) + 1e-15)
    #正则项，lmd就是lambda参数
    reg = (lmd / (2 * m)) * np.sum(np.power(theta[1:], 2))
    
    cost = ((-np.sum(pos + neg)))/m+reg  # 算出代价

    return cost

梯度下降

1
2
3
4
5
6
7
8
9
10
11
def gradient(theta, X, y, lmd):
    m = len(y)   #获取训练样本的数量
    grad = np.zeros(m)

    error = sigmoid(X @ theta) - y  #误差

    grad = (1 / m) * (X.T @ error)  # 计算梯度

    # 正则化项，注意grad[1:]是不包括偏置项的
    grad[1:] += (lmd / m) * theta[1:]  #加上正则化项的梯度
    return grad

grad[1:]: 这是NumPy中的数组切片操作，表示取 grad 数组的从索引1开始的所有元素（即，除了第一个元素以外的所有元素），因为正则化是默认不处理$\theta_0$的

+=: 这是增量赋值操作符，表示将右侧的值加到左侧的变量上。这里将 (learning_rate / m) * theta[1:] 的值加到 grad[1:] 上。

(learning_rate / m) * theta[1:]: 这是一个向量化的操作。它对 theta 中索引从1开始的所有元素应用了学习率和正则化项的操作。这样，一次性对整个向量进行了更新，而不需要显式地使用循环。