正则化

过拟合

在机器学习中，过拟合是指模型在训练数据上表现得太好，以至于在未见过的新数据上表现不佳的现象。

如果我们有非常多的特征，我们通过学习得到的假设可能能够非常好地适应训练集（代价函数可能几乎为0），但是可能会不能推广到新的数据。

以线性回归中的房价预测为例：

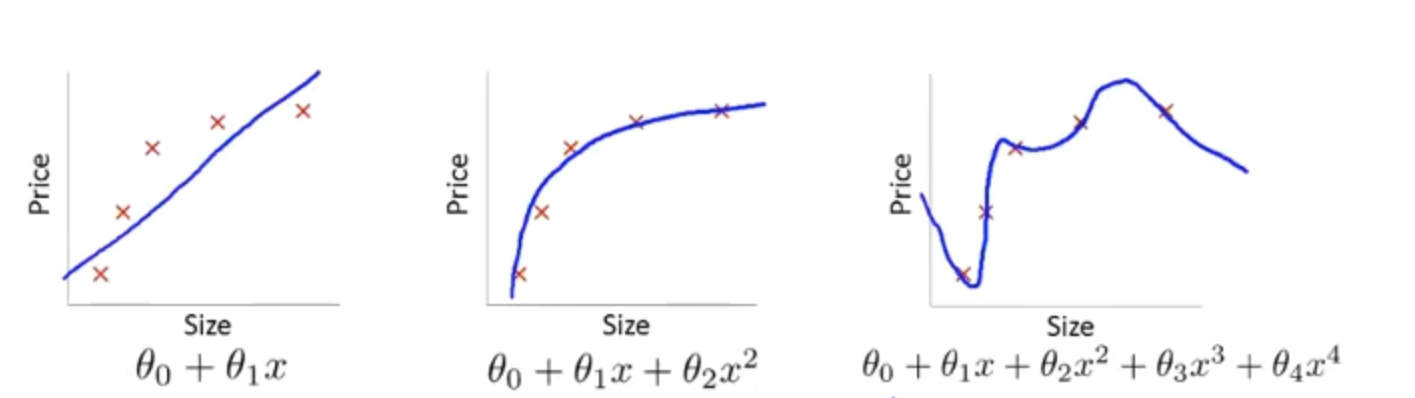
图1是一个线性模型，欠拟合，即不能很好地适应训练集

图3是一个四次方模型，过于强调拟合原始数据，而丢失了算法的本质：预测新数据，可以看出，若给出一个新的值使之预测，它将表现的很差，是过拟合，虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好

图2是一个二次模型，很好的拟合了数据集

分类问题中也存在这样的问题：

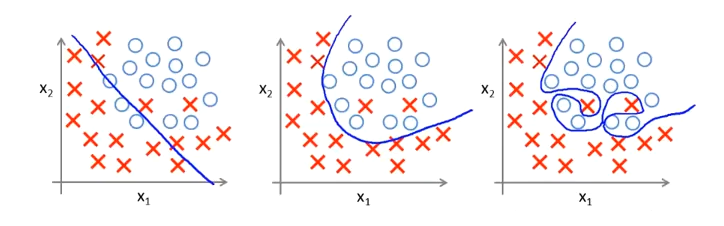
就以多项式理解，$x$ 的次数越高，拟合的越好，但相应的预测的能力就可能变差。

显然图1是欠拟合，图2正好，而图3是过拟合

处理过拟合的问题有以下几种方法：

正则化： 保留所有的特征，但是减少参数的大小。以惩罚模型的复杂性
特征选择：丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如PCA）
交叉验证： 使用交叉验证来评估模型的性能，确保模型在不同的数据子集上都表现良好，而不仅仅是在训练数据上。
增加训练数据： 提供更多的训练数据可以帮助模型更好地学到数据的真实分布，减少过拟合的风险。

代价函数

在房价问题的线性回归中，发生过拟合时，选择的模型是：

${h_\theta}(x) = \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2}^2 + \theta_{3}x_{3}^3 + \theta_{4}x_{4}^4$

正是这些高次项导致了过拟合的产生，所以如果能让这些高次项的系数接近于0的话，解决过拟合的问题

所以要做的就是在一定程度上减小这些参数$\theta $ 的值，这就是正则化的基本思想。如果我们希望减小 ${\theta_{3}}$ 和 ${\theta_{4}}$ 的大小，我们可以通过修改代价函数并对 ${\theta_{3}}$ 和 ${\theta_{4}}$ 进行一定的惩罚来实现。

修改后的代价函数如下：

$cost=\frac{1}{2m}\sum\limits_{i=1}^m{(h_{\theta}( x^{(i)})-y^{(i)})}^2 + 1000\theta_3^2 + 1000\theta_4^2$

优化算法的目标是最小化整个代价函数，因此，为了最小化整个代价函数，算法倾向于选择较小的 $\theta_3$ 和 $\theta_4$，以降低正则化项的值。

通过这样的代价函数选择出的${\theta_{3}}$和${\theta_{4}}$ 对预测结果的影响就比之前要小许多，假如我们有非常多的特征，我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚，并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设：

$J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}{\left(h_{\theta}(x^{(i)}) - y^{(i)}+{\lambda}\sum_{j=1}^{n}{\theta_j^2}\right)^2}$

为了引入正则化，我们添加了一个正则化项，通常是模型参数的平方和，其中 $\lambda$ 是正则化参数，用于控制正则化的强度， $n$ 是模型的参数数量。

注：根据惯例，不对${\theta_{0}}$ 进行惩罚。经过正则化处理的模型与原模型的可能对比如下图所示：

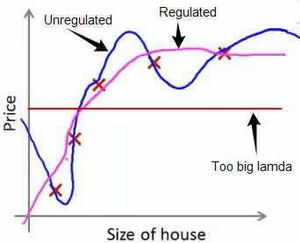
正则化参数$\lambda$ 过大：则会把所有的参数都最小化了，导致模型变成 ${h_\theta}\left( x \right)={\theta_{0}}$，也就是上图中红色直线所示的情况，造成欠拟合。

正则化线性回归

对于线性回归的求解，我们之前推导了两种学习算法：一种基于梯度下降，一种基于正规方程。

正则化线性回归的代价函数为：

$J(\theta) = \frac{1}{2m}\sum_{i=1}^{m} \left( (h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^{n}\theta_j^2 \right)$

如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对$\theta_0$进行正则化，所以梯度下降算法将分两种情形：

$\theta_0 := \theta_0 - a\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)}$ $\theta_j := \theta_j - a\left[\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} + \frac{\lambda}{m}\theta_j\right]$

对上面的算法中$ j=1,2,…,n$ 时的更新式子进行调整可得：

$\theta_j := \theta_j(1 - a\frac{\lambda}{m}) - a\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}$

可以看出，正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令$\theta $值减少了一个额外的值。

正则化逻辑回归

逻辑回归的代价函数为：

$Cost\left( {h_\theta}\left( x \right),y \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[y^{(i)}\log \left( {h_\theta}\left( x^{(i)} \right) \right)+\left( 1-{y^{(i)}} \right)\log \left( 1-{h_\theta}\left( x^{(i)} \right) \right)]}$

同样对于逻辑回归，我们也给代价函数增加一个正则化的表达式，得到代价函数：

$Cost = -\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\log(h_\theta(x^{(i)})) + (1 - y^{(i)})\log(1 - h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2$

要最小化该代价函数，通过求导，得出梯度下降算法为：

看上去同线性回归一样，但是知道 ${h_\theta}\left( x \right)=g\left( {\theta^T}X \right)$，所以与线性回归不同。