逻辑回归

分类问题

分类问题中，预测的变量 $y$ 是离散的值(0or1)，我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法，这是目前最流行使用最广泛的一种学习算法。

将因变量可能属于的两个类分别称为负向类（negative class）和正向类（positive class），则因变量$y\in { 0,1 \\}$ ，其中 0 表示负向类，1 表示正向类。

比如对乳腺癌肿瘤种类的预测：

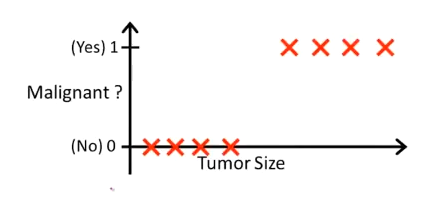
可以用线性回归的方法求出适合数据的一条直线

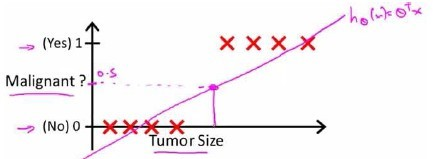
根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出0或1，我们可以预测：

${h_\theta}\left( x \right)>=0.5$时，预测 $y=1$。
${h_\theta}\left( x \right)<0.5$时，预测 $y=0$ 。

对于上图所示的数据，这样的一个线性模型似乎能很好地完成分类任务。假使又观测到一个非常大尺寸的恶性肿瘤，将其作为实例加入到训练集中来，这将获得一条新的直线。

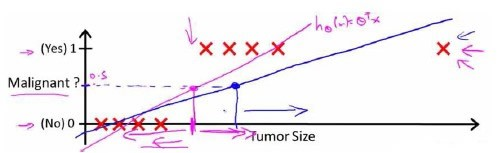
这时，再使用0.5作为阀值来预测肿瘤是良性还是恶性便不合适了。可以看出，线性回归模型，因为其预测的值可以超越[0,1]的范围，并不适合解决这样的问题。

此外，如果我们要用线性回归算法来解决一个分类问题，对于分类， $y$ 取值为 0 或者1，但如果使用的是线性回归，那么假设函数的输出值可能远大于 1，或者远小于0，即使所有训练样本的标签 $y$ 都等于 0 或 1

尽管标签应该最后取值是0 或者1，但是如果算法得到的值远大于1或者远小于0的话，就会感觉很奇怪。所以我们在接下来的要研究的算法就叫做逻辑回归算法，这个算法的性质是：它的输出值永远在0到 1 之间。

假设陈述

引入一个新的模型，逻辑回归，该模型的输出变量范围始终在0和1之间。
逻辑回归模型的假设是： $h_\theta \left( x \right)=g\left(\theta^{T}X \right)$
其中：
$X$ 代表特征向量
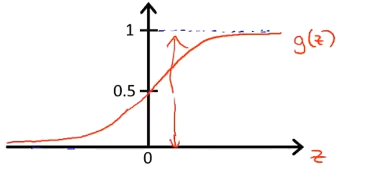
$g$ 代表逻辑函数（logistic function)是一个常用的逻辑函数为S形函数（Sigmoid function），公式为：

$g\left( z \right)=\frac{1}{1+{e^{-z}}}$

该函数的图像为：

合起来，我们得到逻辑回归模型的假设：

$h_\theta\left( x \right)=\frac{1}{1+{e^{-\theta^TX }}}$

$h_\theta \left( x \right)$的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1的概率

例如，如果对于给定的$x$，通过已经确定的参数计算得出$h_\theta \left( x \right)=0.7$，则表示有70%的几率$y$为正向类，相应地$y$为负向类的几率为30%

决策边界

在逻辑回归中，我们预测：

${h_\theta}\left( x \right)>=0.5$时，预测 $y=1$。
${h_\theta}\left( x \right)<0.5$时，预测 $y=0$ 。

据上面绘制出的 S 形函数图像，我们知道当

$z=0$ 时 $g(z)=0.5$
$z>0$ 时 $g(z)>0.5$
$z<0$ 时 $g(z)<0.5$

又 $z={\theta^{T}}x$ ，即：

${\theta^{T}}x>=0$ 时，预测 $y=1$
${\theta^{T}}x<0$ 时，预测 $y=0$

现在假设我们有一个模型：

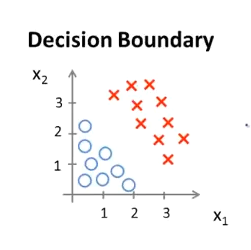
可以用${h_\theta}\left( x \right)=g\left( {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}} \right)$作为模型的分界线，并且参数$\theta$ 是向量[-3 1 1]，则当$-3+{x_1}+{x_2} \geq 0$，即${x_1}+{x_2} \geq 3$时，模型将预测 $y=1$。

我们可以绘制直线${x_1}+{x_2} = 3$，这条线便是我们模型的分界线，将预测为1的区域和预测为 0的区域分隔开

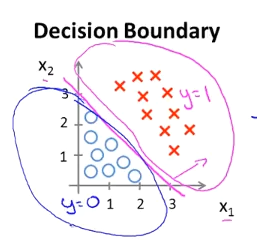
可以用非常复杂的模型来适应非常复杂形状的判定边界

代价函数

对于线性回归模型，定义的代价函数是所有模型误差的平方和。

$J(θ_0,θ_1)=\frac{1}{2m}\sum\limits_{i=1}^m(h_θ(x^{(i)})−y^{(i)})^2$

理论上来说，也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将${h_\theta}\left( x \right)=\frac{1}{1+{e^{-\theta^{T}x}}}$带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数

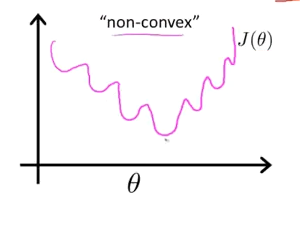
这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值

所以为了避免这个问题，重新定义逻辑回归的代价函数为：$J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^m{Cost\left( {h_\theta}\left( x^{\left( i \right)} \right),y^{\left( i \right)} \right)}$，其中：

$Cost(h_{\theta}(x),y) = \begin{cases} -log\left( {h_\theta}\left( x \right) \right) & \text{if }y=1 \\ -log\left( 1-{h_\theta}\left( x \right) \right), & \text{if }y=0 \end{cases}$

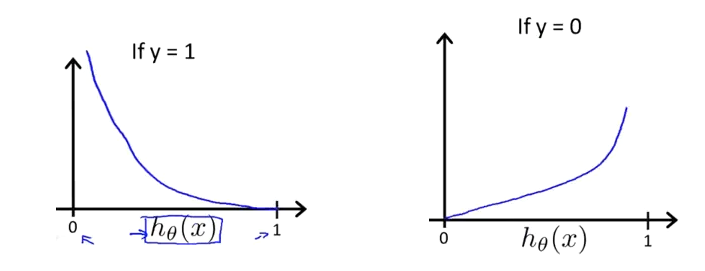
这样构建的$Cost\left( {h_\theta}\left( x \right),y \right)$函数的特点是：

当实际的 $y=1$ 且${h_\theta}\left( x \right)$也为 1 时代价为 0，当 $y=1$ 但${h_\theta}\left( x \right)$不为1时误差随着${h_\theta}\left( x \right)$变小而变大
当实际的 $y=0$ 且${h_\theta}\left( x \right)$也为 0 时代价为 0，当$y=0$ 但${h_\theta}\left( x \right)$不为 0时误差随着 ${h_\theta}\left( x \right)$的变大而变大

可以合并$Cost\left( {h_\theta}\left( x \right),y \right)$：

$Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right)$

即，逻辑回归的代价函数：

$Cost\left( {h_\theta}\left( x \right),y \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[y^{(i)}\log \left( {h_\theta}\left( x^{(i)} \right) \right)+\left( 1-{y^{(i)}} \right)\log \left( 1-{h_\theta}\left( x^{(i)} \right) \right)]}$

梯度下降

为了找出让$Cost\left( {h_\theta}\left( x \right),y \right)$最小的$\theta$ 参数，需要使用梯度下降法

即：

$\theta_j:=\theta_j-\alpha\frac{\partial{J(θ_0,θ_1)}}{\partial{\theta_j}}$

而

$J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{y^{(i)}}\log \left( {h_\theta}\left( {x^{(i)}} \right) \right)+\left( 1-{y^{(i)}} \right)\log \left( 1-{h_\theta}\left( {x^{(i)}} \right) \right)]}$

对$J\left( \theta \right)$求偏导数，结果是：（数学推导过程略）

$\frac{\partial }{\partial \theta _j}J(\theta)=\frac{1}{m}{\sum_{i=1}^m(( h_\theta (x^{(i)}})-y^{(i)})\cdot x^{(i)})$

那么，梯度下降法的公式为：

${\theta_j}:={\theta_j}-\alpha \frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}(x^{(i)})-{y^{(i)}}){x_j}^{(i)}}$

和线性回归梯度下降一模一样，但是线性回归和逻辑回归不是同一个算法，因为假设函数是不一样的

对于线性回归的假设函数：${h_\theta}\left( x \right)={\theta^T}X={\theta_0}{x_0}+{\theta_1}{x_1}+{\theta_2}{x_2}+…+{\theta_n}{x_n}$
对于逻辑函数假设函数：${h_\theta}\left( x \right)=\frac{1}{1+{e^{-{\theta^T}X}}}$

高级优化

梯度下降并不是我们可以使用的唯一算法，还有其他一些算法，更高级、更复杂。如果能用这些方法来计算代价函数$J\left( \theta \right)$和偏导数项$\frac{\partial }{\partial {\theta_j}}J\left( \theta \right)$两个项的话，那么这些算法就是为我们优化代价函数的不同方法，共轭梯度法 BFGS (变尺度法) 和L-BFGS (限制变尺度法) 就是其中一些更高级的优化算法，它们需要有一种方法来计算 $J\left( \theta \right)$，以及需要一种方法计算导数项，然后使用比梯度下降更复杂的算法来最小化代价函数

并不需要知道这些算法的细节，只要会需要使用就行

在python中，如果想使用BFGS算法求解优化问题，需要先导入scipy库

SciPy是一个开源的Python算法库和数学工具包。它基于Numpy，用于数学、科学、工程学等领域。包含的模块有最优化、线性代数、积分、插值、特殊函数、快速傅里叶变换、信号处理和图像处理、常微分方程求解和其他科学与工程中常用的计算

1	import scipy.optimize as opt

这里导入scipy中opt模块，然后介绍一下opt中的fmin_bfgs函数

opt.fmin_bfgs(f, fprime, x0, maxiter, full_output, disp,args,gtol,norm，epsilon，callback,retall)

f：这是你要最小化的目标函数，函数只能有一个参数
fprime：这是目标函数的梯度，也就是导数。如果你没有提供，那么函数会使用近似值。
x0：这是参数的初始猜测值
maxiter：这是最大迭代次数，即算法尝试找到最小值的步数。
full_output：如果为True，则返回所有输出结果，包括最优解、最小值、梯度的最小值、逆Hessian矩阵、函数调用次数、梯度调用次数、警告标志以及每次迭代的结果列表。
disp：如果为True，则打印收敛信息。
args：这是传递给f和fprime的额外参数。
gtol：这是梯度范数的阈值，如果梯度范数小于这个值，那么算法就会停止。
norm：这是用于计算梯度范数的范数的阶数。
epsilon：如果fprime是近似的，那么这个值就是步长。
callback：这是一个可选的用户提供的函数，每次迭代后都会被调用。调用的形式是callback(xk)，其中xk是当前的参数向量。
retall：如果为True，则返回每次迭代的结果列表。

实例代码：

1	theta, cost, *unused = opt.fmin_bfgs(f=cost_func, x0=initial_theta, maxiter=400, full_output=True, disp=False)

在这个例子中：

f=cost_func：最小化的目标函数名字叫cost_func，需要实现写好目标函数
x0=initial_theta：这是参数的初始猜测值initial_theta
maxiter=400：这是最大迭代次数，即算法尝试找到最小值的步数。
full_output=True：如果为True，则返回所有输出结果，包括最优解、最小值、梯度的最小值、逆Hessian矩阵、函数调用次数、梯度调用次数、警告标志以及每次迭代的结果列表。
disp=False：如果为True，则打印收敛信息。

返回值theta, cost, *unused是一个元组，其中：

theta是最小化函数的参数$\theta$，即最优解。
cost是最小值，即目标函数在最优解处的值。
*unused是其他返回值，包括梯度的最小值、逆Hessian矩阵、函数调用次数、梯度调用次数、警告标志以及每次迭代的结果列表。由于不需要这些值，所以可以使用*unused来忽略它们。

多类分类

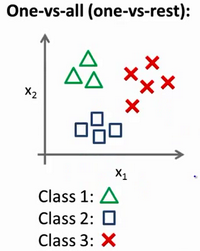
现在有一个训练集，好比上图表示的有3个类别，我们用三角形表示 $y=1$，方框表示$y=2$，叉叉表示 $y=3$。我们下面要做的就是使用一个训练集，将其分成3个二元分类问题。

如下图所示的那样，要拟合出一个合适的分类器。

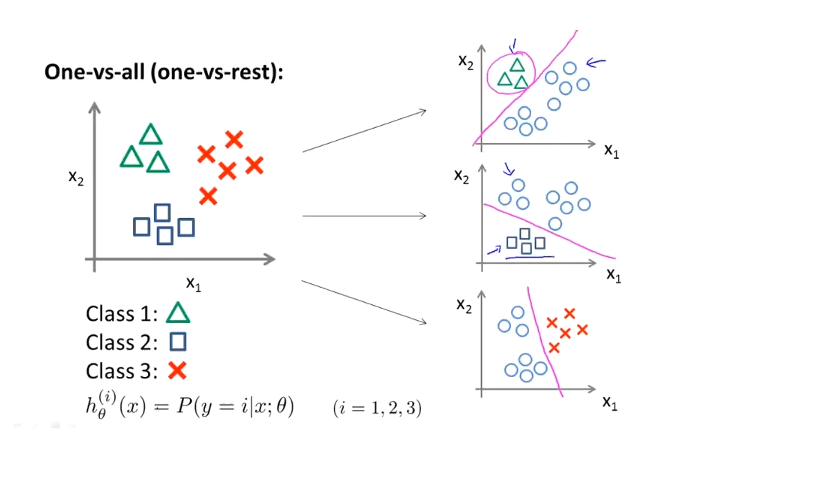
方法是先将两个类看做是同一个类，这样问题就变成了二元分类问题，可以求出决策边界，然后重复此方法，画出多个决策边界，从而选出拟合质量最好的边界