ex1:linear regression

概述

在这部分练习中，您将使用一个变量进行线性回归，以预测一辆餐车的利润。假设您是一家餐饮连锁店的首席执行官，正在考虑在不同城市开设新的分店。该连锁店已在多个城市拥有餐车，您也掌握了这些城市的利润和人口数据。

必要的文件如下：

ex1.py-引导您完成练习的Python文件
ex1data1.txt -单变量线性回归的数据集
computeCost.py-计算线性回归成本的函数
gradientDescent.py-运行梯度下降的函数

导入

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from matplotlib.colors import LogNorm
from computeCost import *
from gradientDescent import *

在Python中，from computeCost import *是一种导入语句，用于从computeCost模块导入所有的公共对象（例如函数、类、变量等）。这意味着你可以直接使用这些对象，而无需通过模块名来引用它们。

例如，假设computeCost模块中有一个函数compute_cost()，那么你可以直接调用compute_cost()，而不需要写成computeCost.compute_cost()

读取并绘图

1
2
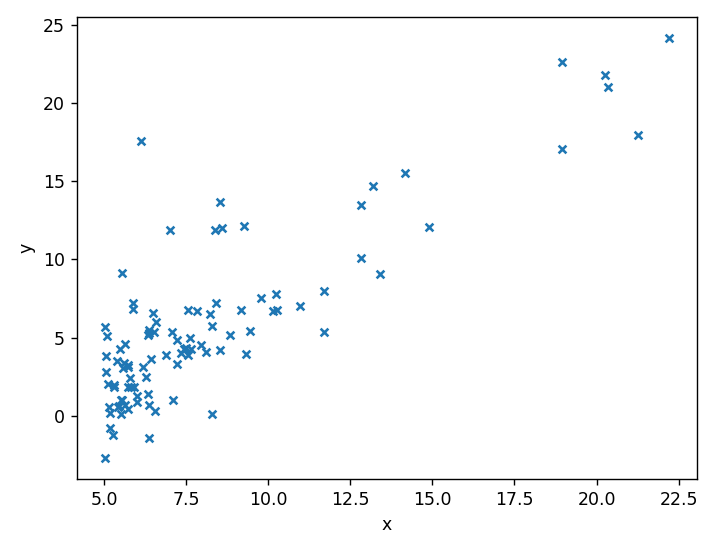
3

data=pd.read_csv('ex1data1.txt',header=None,names=['x','y'])
plt.plot(data['x'],data['y'],'x')
plt.show()

pd.read_csv函数表示：读取ex1data1.txt这个文件，header=None表示第一行是数据，而不是列名，names=['x','y']意味着DataFrame将有两列，第一列的列名是x，第二列的列名是y。

plt.plot函数表示，横轴的数据是data中名字叫x的列，纵轴的数据是data中名字叫y的列，散点的标记是x图案

梯度下降

插入$x_0$参数列

1	data.insert(0,'one',1)

在data的第1列，插入元素为1的列，并且把这列的名字命名为one

在多变量线性回归这一节的开头，解释了原因：

多元线性回归时的映射$h$被表述为：
$h_{\boldsymbol{\theta}}(x)=\theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n\\$
这个公式中有$n+1$个参数和$n$个变量，为了表述的方便，我们会在样本中新增一个特征量记为$x_0^{(i)}=1,(i=1,2,\cdots,n)$，则公式转化为：
$h_{\theta} \left( x \right)={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}$
在此情况下只需要定义这样的两个向量：
$\boldsymbol{x}=\begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}\in\mathbb{R}^{n+1}, \boldsymbol{\theta}=\begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{bmatrix}\in\mathbb{R}^{n+1}\\$
就可以将前面的映射表述为向量内积的形式：
$h_{\boldsymbol{\theta}}(\boldsymbol{x})=\boldsymbol{\theta}^T\boldsymbol{x}\\$

插入$x_0=1$的列，可以将$h_{\boldsymbol{\theta}}$变为向量内积的形式，便于$\theta$的计算

print(data.head()) 
"""
    one   x        y
0    1  6.1101  17.5920
1    1  5.5277   9.1302
2    1  8.5186  13.6620
3    1  7.0032  11.8540
4    1  5.8598   6.8233
"""

展示data的前5行，看一下是否是我们所设置的那样，可以看到有3列，名字分别是one，x，y

代价函数

col=data.shape[1]
X=data.iloc[:,0:col-1]
y=data.iloc[:,col-1]
theta=np.zeros(col-1)

data.shape[1]表示的是data列的数量，赋值给col，实际上是3

接下来使用了Pandas的iloc函数的切片语法

X：表示data的前两列，即$x_0$和$x_1$的数据
y：表示data的最后一列，即最后的y的数据
theta：使用numpy中的zeros函数，初始化成了[0,0]形式，数量和x的个数肯定是相等的

接下来，编写computeCost.py文件中的compute_cost(X, y, theta)函数，计算代价

代价函数的计算公式是：

$J(θ_0,θ_1)=\frac{1}{2m}\sum\limits_{i=1}^m(h_θ(x^i)−y^i)^2$

import numpy as np

def compute_cost(X, y, theta):
    # Initialize some useful values
    inner = np.power(((X @ theta) - y), 2)
    return np.sum(inner) / (2 * len(X))

X是一个$(n,2)$的数组，y是一个$(n,1)$的数组，thetas是一个$(2,)$的数组，X @ theta就表示了$h_{\boldsymbol{\theta}}(\boldsymbol{x})=\boldsymbol{\theta}^T\boldsymbol{x}$，其中@的意思是要用矩阵乘法，而不是元素乘法，X @ theta会让X中的每一行都和theta中元素做点积，即计算结果是一个$(n,1)$的数组

np.power是幂的计算函数，参数为2，意味求$h_{\boldsymbol{\theta}}(\boldsymbol{x})-y$的二次幂，因为是数组的运算，所以把数组中每个元素都变为其二次幂的形式

np.sum将数组中每个元素全部都相加在一起，最后除以2倍X数组的元素个数，即为$\frac{1}{2m}$

再回到ex1.py文件中来，将之前写的X，y，theta代入到compute_cost函数中去

1 2	print(compute_cost(X, y, theta)) #结果是32.07

完全符合预期

梯度下降

在编写梯度下降函数之前，先设置参数，这里吧迭代次数iterations设置成1500次，学习率alpha设置为0.01

1 2	iterations = 1500 alpha = 0.01

再编写gradient_descent.py中的gradient_descent(X, y, theta, alpha, iters)函数，完成梯度下降功能

def gradient_descent(X, y, theta, alpha, iters):
    m = len(y)
    cost = np.zeros(iters)

    # 迭代
    for i in range(iters):
        # 预测
        y_pred = X @ theta

        # 计算误差
        error = y_pred - y

        # 计算代价
        cost[i] = compute_cost(X, y, theta)

        # 更新每个参数
        theta -= (alpha / m) * (X.T @ error)

    return theta, cost

设置一个大小为iters的数组cos，用来记录每次迭代theta所产生的代价

在一个执行iters(1500)次的循环中，

y_pred表示模型的预测值即$h_{\boldsymbol{\theta}}(\boldsymbol{x})=\boldsymbol{\theta}^T\boldsymbol{x}$
error表示模型和真实值的误差： $\boldsymbol{\theta}^T\boldsymbol{x}- y$
cost[i] = compute_cost(X, y, theta)：将每次theta的参数代入代价函数中计算代价
theta -= (alpha / m) * (X.T @ error)：这里直接就是矩阵之间的减法，对应元素会直接相减，体现了矢量化的思想

梯度下降的公式

$\theta_j:=\theta_j-\alpha\frac{\partial{J(θ_0,θ_1)}}{\partial{\theta_j}}$
其中
$\frac{\partial }{\partial \theta _j}J(\theta_0,\theta_1)=\frac{1}{m}{\sum_{i=1}^m(( h_\theta (x^{(i)}})-y^{(i)})\cdot x^{(i)})$
即
$\theta_j:=\theta_j-\alpha\frac{1}{m}{\sum_{i=1}^m(( h_\theta (x^{(i)}})-y^{(i)})\cdot x^{(i)})$

最后返回一个theta数组和一个cost数组，theta里面的$\theta$值就是梯度下降1500次过后的$\theta$

回到ex1.py中，接下来调用gradient_descent函数

1
2
3

theta,cost= gradient_descent(X, y, theta, alpha, iterations)
print(theta)
#[-3.63029144  1.16636235]

输出theta，结果符合预期

再根据梯度下降后的theta数组，绘制拟合曲线

pred=X@theta.T   #根据x值预测出的y值
plt.plot(data['x'], pred,'r',label='Linear Regression') 
plt.ylabel('Profit')  #设置y轴名称
plt.xlabel('Population')   #设置x轴名称
plt.title('Profit and Population') # 设置标题
plt.legend()  #展示图例
plt.show()  #展示图像

把预测值$h_{\boldsymbol{\theta}}(\boldsymbol{x})=\boldsymbol{\theta}^T\boldsymbol{x}$插入到data的第4列中去，这样做是因为，Pandas的plot函数必须要使用Pandas对象中的列作为参数

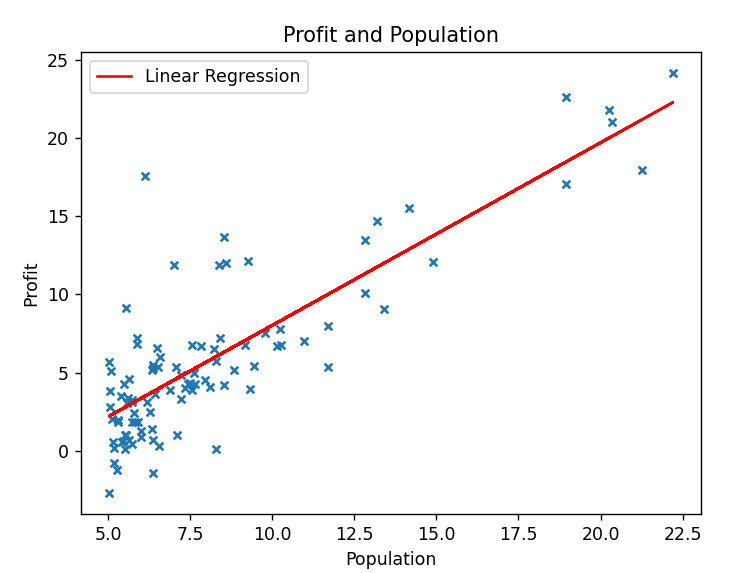
plot函数将名称为x的列作为横轴，把pred作为纵轴，曲线命名为Linear Regression，颜色为红色，绘制图像

设置x，y轴的名称，图像标题，展示图例，展示图像后：

再展示cost数组的内容，将梯度下降的内容展示出来

1 2	plt.plot(np.arange(1500),cost) plt.show()

把0~1500的连续值设置为x轴，把cost的值设置为y轴，绘制并展示图像

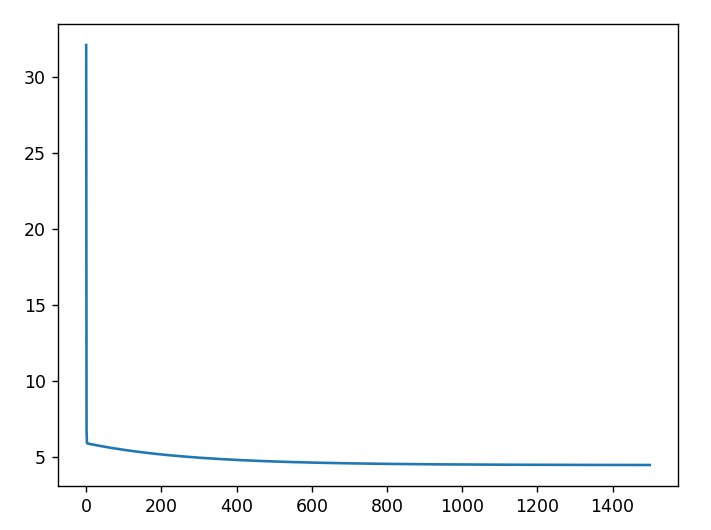
可以看到，经过1500次的迭代，代价cost在逐渐接近0，说明拟合效果很好

最后我们解决一下实际问题，预测一下Population为35000的城市，利润有多少？

1
2
3

predict=np.array[1,3.5]@theta  
print(predict*10000)
#结果是4519.768