3.多变量线性回归
多变量线性回归
多维特征
表示方法
目前为止,我们探讨了单变量/特征的回归模型,现在我们对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为$\left( {x_{1}},{x_{2}},…,{x_{n}} \right)$。
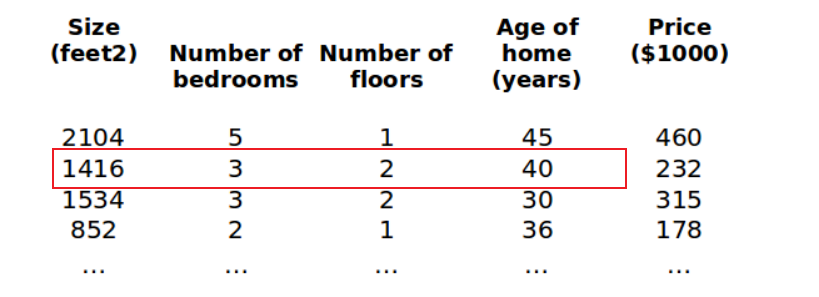
增添更多特征后,我们引入一系列新的注释:
$n$代表特征的数量
$x^{(i)}$代表第$i$个训练实例,是特征矩阵中的第$i$行
比方说,上图的${x}^{(2)}\text{=}\begin{bmatrix} 1416\\ 3\\ 2\\ 40 \end{bmatrix}$
$x_j^{(i)}$ 代表特征矩阵中第 $i$ 行的第 $j$ 个特征,也就是第 $i$ 个训练实例的第 $j$ 个特征。
如上图的$x_{2}^{\left( 2 \right)}=3,x_{3}^{\left( 2 \right)}=2$
于是多元线性回归时的映射$h$被表述为:
这个公式中有$n+1$个参数和$n$个变量,为了表述的方便,我们会在样本中新增一个特征量记为$x_0^{(i)}=1,(i=1,2,\cdots,n)$,则公式转化为:
在此情况下只需要定义这样的两个向量:
就可以将前面的映射表述为向量内积的形式:
这也就是多元线性回归(Multivariate linear regression)的一般形式。我们同样也可以定义在多元线性回归下的代价函数:
于是可以写出多元线性回归情况下的梯度下降方法:
特征缩放
面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛
以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000平方英尺,而房间数量的值则是0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图,图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。
一般来说就是将所有特征都约束到[-1,1]区间之内,这样可以使得梯度下降的时候每个特征对于梯度的贡献量相近从而使得梯度下降的时候在空间中的路径相对比较平直,加快梯度下降的速度。
有的时候还会在此基础上进行均值标准化,就是将每个变量都减去样本均值然后再归一化(除以样本最大值与最小值之间的差)到相同区间内(注意不要对 $x_0$ 进行这样的操作):
学习率
学习率的设置影响梯度下降的效率
- 学习率太小——梯度下降太慢
- 学习率太大——代价函数可能不收敛甚至发散
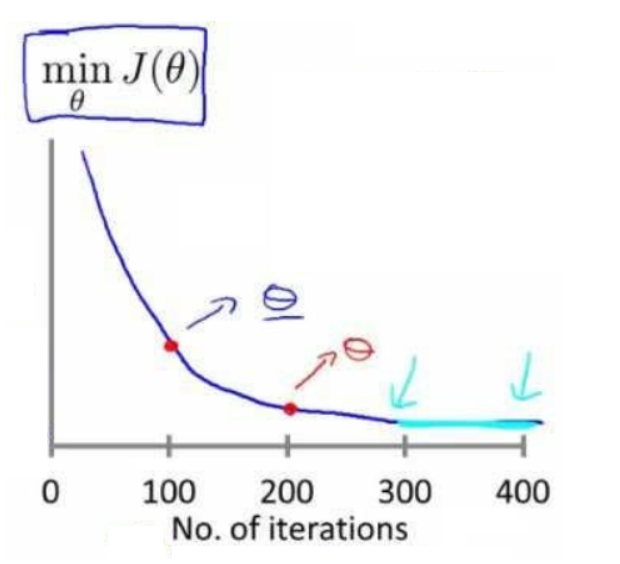
检查梯度下降算法是否正常收敛的典型方法:
- 在训练过程中绘制代价函数-迭代次数曲线,当该曲线进入比较平坦的阶段的时候就说明梯度下降基本已经收敛
- 设置自动收敛测试:如果一次迭代中代价函数的变化率小于$10^{-3}$就自动判定为已经收敛。【但是这个阈值的选取比较困难
特征和多项式回归
有时候可以将特征融合起来,组成一个新的特征,比如在房价问题中,房屋的临街宽度和纵向深度都是特征,可以组合成一个新的特征——面积

$h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}\times{frontage}+{\theta_{2}}\times{depth}$
${x_{1}}=frontage$(临街宽度),${x_{2}}=depth$(纵向深度),$x=frontage*depth=area$(面积),则:${h_{\theta}}\left( x \right)={\theta_{0}}+{\theta_{1}}x$。
到目前为止,我们假设的学习算法都是:$h_{\theta}\left( x \right)={\theta_0}+{\theta_1}x$ 的形式,其图形都是一条直线,线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如:
抛物线模型:$h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}$
或者三次方模型: $h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}+{\theta_{3}}{x_{3}^3}$
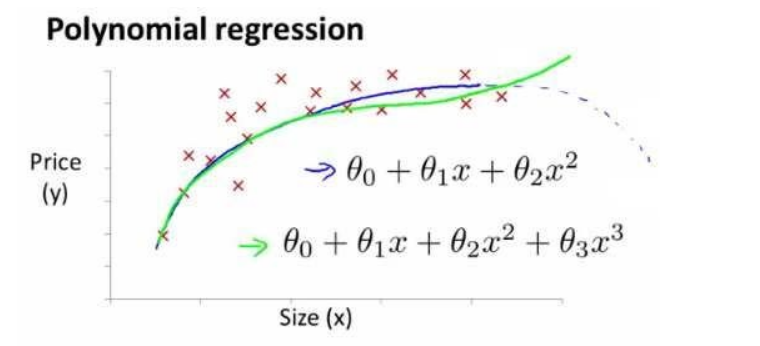
通常我们需要先观察数据然后再决定准备尝试怎样的模型。 另外,我们可以令:
${x_2}=x_2^2,x_3=x_3^3$,从而将模型转化为线性回归模型。
根据函数图形特性,我们还可以使:
${h_\theta}(x)={\theta_0}\text{+}{\theta_1}(size)+{\theta_2}{(size)^2}$
或者:
${h_\theta}(x)={\theta_0}\text{+}{\theta _1}(size)+{\theta _2}\sqrt{size}$
注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。
正规方程
到目前为止,我们都在使用梯度下降算法,但是对于某些线性回归问题,正规方程方法是更好的解决方案。
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的:$\frac{\partial}{\partial{\theta_{j}}}J\left( {\theta_{j}} \right)=0$ 。 假设我们的训练集特征矩阵为 $X$(包含了 $x_0=1$)并且我们的训练集结果为向量 $y$
在多组训练样本下上面方程可以扩展为向量方程:
那么可以写出这个方程的正规方程解(不需要特征缩放)为:
这里的设计矩阵 $X$ 实际上就是把输入特征转置以后叠放在一起:
以下表示数据为例:
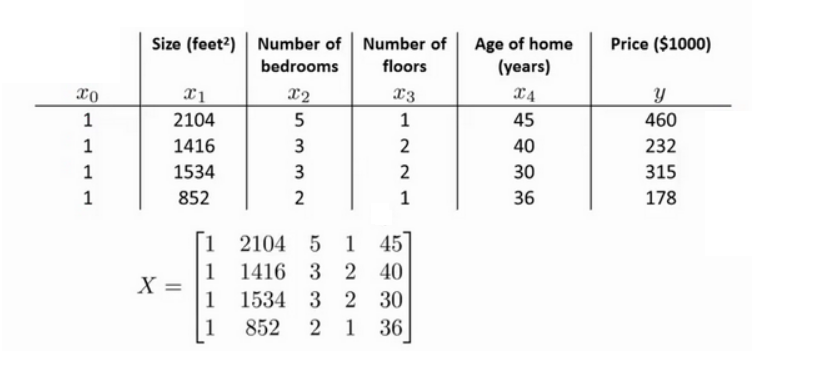
可以直接运用正规方程法求解参数:
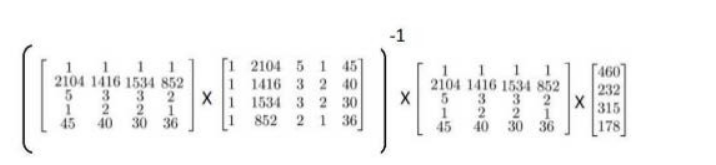
结果会是一个 $4×1$的 $\theta$ 矩阵
注:对于那些不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征,也有可能是特征数量大于训练集的数量),正规方程方法是不能用的。
总结
梯度下降与正规方程的比较:
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率$\alpha$ | 不需要 |
| 需要多次迭代 | 一次运算得出 |
| 当特征数量$n$大时也能较好适用 | 需要计算${\left( {X^T}X \right)}^{-1}$ 如果特征数量$n$较大则运算代价大,因为矩阵逆的计算时间复杂度为$O\left( {n^3} \right)$,通常来说当$n$小于10000 时还是可以接受的 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |


