相似矩阵及二次型

特征值

定义

一般情况下，向量经过线性映射后，方向发生改变

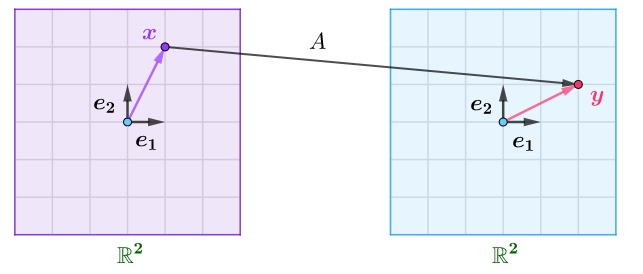
不过，有可能部分向量，在线性映射后方向没有改变，只是发生了伸缩：

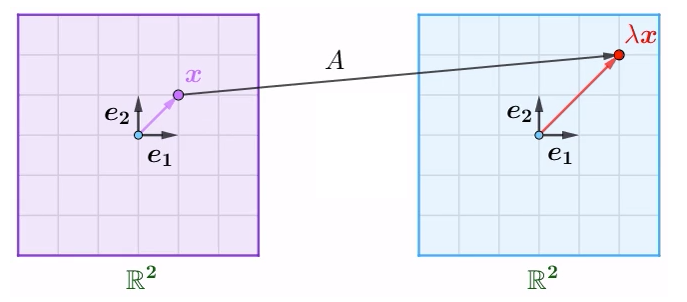
这些没有发生方向改变的向量，称为特征向量，变换前后的伸缩比称为特征值，其严格定义如下：

设$A$是$n$阶方阵，$\boldsymbol{x}$为非零向量，若存在数$\lambda$使得下式成立：

$A\boldsymbol{x}=\lambda\boldsymbol{x}$

那么将数$\lambda$称为$A$的特征值，非零向量$\boldsymbol{x}$称为$A$的对应于$\lambda$的特征向量。

单位阵

对于$n$阶单位阵$I$始终有：

$\boldsymbol{I}\boldsymbol{x}=\boldsymbol{x},\quad \boldsymbol{x}\in\mathbb{R}^n$

意味着向量空间$R^n$中所有向量(除了零向量)$x$都是单位阵$I$的特征向量

求法

$A\boldsymbol{x}=\lambda\boldsymbol{x}$

经过转换后：

$\begin{align} A\boldsymbol{x}=\lambda\boldsymbol{x} &\iff AI\boldsymbol{x}=\lambda I\boldsymbol{x}\\ &\iff (AI-\lambda I)\boldsymbol{x} = \boldsymbol{0}\\ &\iff (A-\lambda I)\boldsymbol{x} = \boldsymbol{0} \end{align}$

假设存在特征值和特征向量，那么上述方程必然有非零解。因此根据解的个数可知，系数矩阵$A-\lambda I$必然不是满秩矩阵（否则$(A-\lambda I)\boldsymbol{x} = \boldsymbol{0}$只有唯一解，该唯一解就是零向量，根据定义，特征值和特征向量不能是零向量），再结合上满秩与行列式的关系，此时必然有：

$|A-\lambda I|=0$

这样就有两个式子了，可以解出要求的两个未知数：

$\begin{cases}|A-\lambda I| = 0\\\\ (A-\lambda I)\boldsymbol{x} = \boldsymbol{0} \end{cases}\Longrightarrow \begin{cases}\lambda = ? \\\\ \boldsymbol{x} = ?\end{cases}$

根据二阶行列式的计算方法可以直接算出$\lambda$的值，算出$\lambda$的值后，将$\lambda$带入到$(A-\lambda I)\boldsymbol{x} = 0$,利用求解集的方法，算出$x$的解集，带入不同的$\lambda$即可求出不同的特征向量

假设解集

$\boldsymbol{x}_{\lambda=0}=k\begin{pmatrix}-1\\1\end{pmatrix},k\in\mathbb{R}$

意味着特征值为0对应的特征向量（零向量除外），将它画出来就是下图定义域中的绿线，其上的任意向量都会被映射到零点：

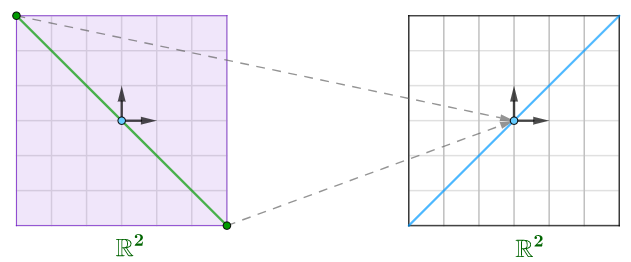
很显然，图中的绿线是一个向量空间，因为其中都是特征值为 0 的特征向量（零向量除外），所以也称为特征值为 0 的特征空间

而判定向量$x$是否是矩阵$A$的特征向量的方式很简单，只需要将$Ax$相乘，如果结果可以化成$\lambda x$的形式，就是特征向量

已知$A$,某个特征向量$x$，可以根据$Ax=\lambda x$求列方程求解$\lambda$，以及$A$中的未知数

性质

转置矩阵与原矩阵特征值相同
行列式的值=特征值的乘积，所以如果$|A|=0$，那么必有一个特征值为0
矩阵的特征值等于逆矩阵特征值的倒数
若$\lambda_1,\lambda_2,\cdots,\lambda_n$为$n$阶方阵$\boldsymbol{\boldsymbol{A}}$的特征值，则：

$|\boldsymbol{A}|=\lambda_1\lambda_2\ldots\lambda_n$

矩阵的特征值和矩阵对角线元素之和(迹)相同，即：
$∑\lambda _i=∑a_{ii}$
证明过程

证明如下：

$\boldsymbol{A}$的特征值多项式为：
$|\boldsymbol{A}-\lambda \boldsymbol{I}|=\begin{vmatrix} a_{11}-\lambda & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22}-\lambda & \cdots & a_{2n}\\ \vdots&\vdots&\quad&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}-\lambda \end{vmatrix}$
可以观察出，$\lambda^{n-1}$的项只能产生于主对角线的乘积。因为主对角线乘积为：
$(a_{11}-\lambda)(a_{22}-\lambda)\cdots (a_{nn}-\lambda)$
根据二项式定理可得$\lambda^{n-1}$的系数为$(a_{11}+a_{22}+\cdots + a_{nn})$

由于$\lambda_1,\lambda_2,\cdots,\lambda_n$是该矩阵的特征值，所以：
$|\boldsymbol{A}-\lambda \boldsymbol{I}|=(\lambda_1-\lambda)(\lambda_2-\lambda)\cdots(\lambda_n-\lambda)$
根据二项式定理可得$\lambda^{n-1}$的系数为$(\lambda_{1}+\lambda_{2}+\cdots + \lambda_{n})$

$\lambda^{n-1}$的系数必然是相等的，所以：
$tr(\boldsymbol{A})=a_{11}+a_{22}+\cdots +a_{nn}=\lambda_1+\lambda_2+\cdots +\lambda_n$
根据特征多项式：若$λ$是矩阵$A$的特征值，则$f(λ)$就是多项式矩阵$f(A)$的特征值

定理：

已知$\lambda_1,\lambda_2,\cdots,\lambda_m$是$n$阶方阵$A$相异的特征值，以及$\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_m$是$\lambda_1,\lambda_2,\cdots,\lambda_m$对应的特征向量，则向量组$\{\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_m\}$线性无关。

反过来说，如果特征值$\lambda_1$对应了多个特征向量，那么这些特征向量的组合仍然是方阵$A$的特征向量

如果矩阵A能被拆分成$A=(a-1)E+B$，利用$rank(B)=1$求$B$的特征值和特征向量比较方便

结论：n阶矩阵A，r(A)=1，则A的特征值一个是A的迹（主对角元素和），其余都是0

证0是n-1重特征根：

因为$r(A)=1$，$A$的行列式为0，又因为行列式等于特征值的乘积，所以0必为$A$特征值

求0对应的特征向量，$Ax=0x=0$，则求0对应的特征向量即求$Ax=0$的解

$r(A)=1，Ax=0$必有$n-1$个线性无关解向量，那么0至少为$n-1$重特征根

证A的迹为一个特征值：

$r(A)=1$，则$A$必可表示成一个列向量和一个行向量的乘积，设$α$和$β$为列向量 ($T$表示转置)（因为$A$的秩为1，所以α和β不可能为零向量）

则$A=αβ^T，Aα = αβ^Tα = α(β^Tα) = (β^Tα)α$

则$β^Tα$是$A$特征值，特征向量为$α$

相似矩阵

定义

设$A$，$B$都是$n$阶方阵，若有可逆矩阵$P$，使得

$\boldsymbol{B}=\boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P}$

则称$\boldsymbol{P}$为相似变换矩阵，称$\boldsymbol{B}$是$\boldsymbol{A}$的相似矩阵，记作：

$\boldsymbol{A}\simeq \boldsymbol{B}$

单解释下上述定义，如果$\boldsymbol{A}$和$\boldsymbol{B}$是相似矩阵，那么两者实际上是同一个线性映射在不同基下的代数表示(需要参考)：

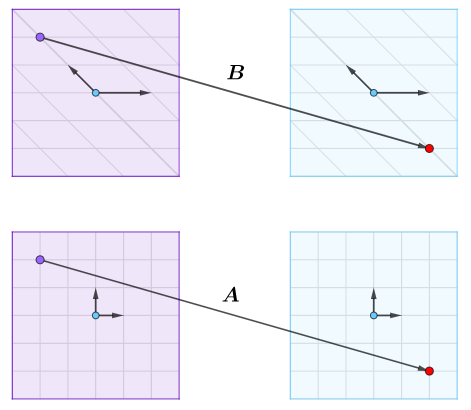
在自然基下，上述向量的坐标分别是$[\boldsymbol{x}]_\mathcal{E}$和$[\boldsymbol{y}]_\mathcal{E}$，上述线性映射可用矩阵$\boldsymbol{A}$来表示，即有$\boldsymbol{A}[\boldsymbol{x}]_\mathcal{E}=[\boldsymbol{y}]_\mathcal{E}$。或者图示如下：

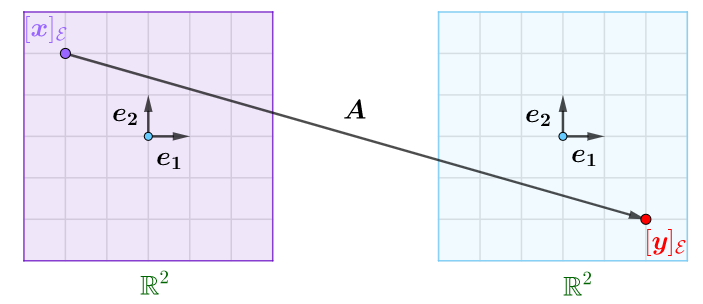
或者在基$\mathcal{P}$，上述向量的坐标分别是$[\boldsymbol{x}]_\mathcal{P}$和$[\boldsymbol{y}]_\mathcal{P}$，上述线性映射可用矩阵$\boldsymbol{B}$来表示，即有$\boldsymbol{B}[\boldsymbol{x}]_\mathcal{P}=[\boldsymbol{y}]_\mathcal{P}$。或者图示如下：

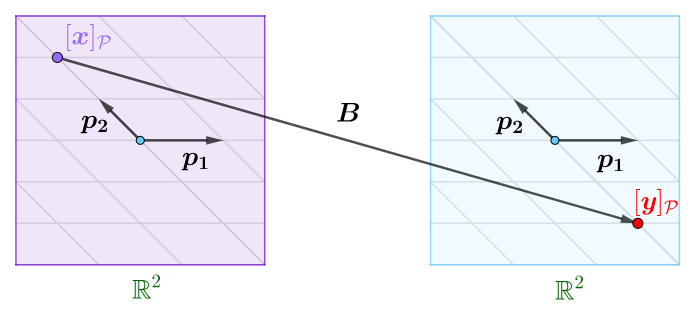
上面的矩阵$A$和矩阵$B$就是同一个线性映射在不同基下的代数表示

如果存在可逆矩阵$P$,也就是存在过渡矩阵$P$，通过坐标变换公式：

$[\boldsymbol{x}]_\mathcal{E}=\boldsymbol{P}[\boldsymbol{x}]_\mathcal{P},\quad [\boldsymbol{y}]_\mathcal{P}=\boldsymbol{P}^{-1}[\boldsymbol{y}]_\mathcal{E}$

那么矩阵$\boldsymbol{A}$和矩阵$\boldsymbol{B}$就可通过过渡矩阵$\boldsymbol{P}$联系起来，此时$\boldsymbol{A}$和$\boldsymbol{B}$就是相似矩阵：

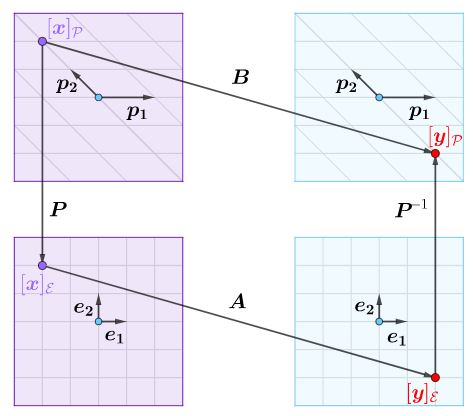
相似矩阵集合了基变换和坐标变换

性质

若$A\simeq B$，则：

$A^k\simeq B^k,\quad k\in\mathbb{Z}^+ A^\mathrm{T}\simeq B^\mathrm{T}$

若$A\simeq B$，且$A、B$可逆，则：

$A^{-1}\simeq B^{-1} A^*\simeq B^*$

若$A\simeq B，B\simeq C$，那么：

$A\simeq C$

相似对角化

当需要算矩阵的高次幂时$A^n$，直接计算会变得非常复杂,但是对角矩阵的高次幂就很好算：

$\Lambda^n=\begin{pmatrix}a_{11}&0\\0&a_{22}\end{pmatrix}^n=\begin{pmatrix}a_{11}^n&0\\0&a_{22}^n\end{pmatrix}$

而把常规矩阵变为对角矩阵的步骤，叫做对角化

条件

$\Lambda\sim A$，就直接说明了可相似对角化，即有$k$个线性无关的特征向量
实对称矩阵可相似对角化；
方阵的$n$个特征值彼此都不相同，也就是都是单根的话，则矩阵可相似对角化，如果有重根，看第三种情况；
验证$k$重根是不是具备$k$个线性无关的特征向量，也就是看$A-λE$或$λE-A$的秩是否等于$n-k$，若相等，则矩阵可相似对角化，不相等，则不能进行相似对角化。即几何重数＝代数重数才能对角化。单重特征根的几何重数＝代数重数＝1。

步骤

如果$n$阶方阵$A$有$n$个线性无关的特征向量$\boldsymbol{p_1},\boldsymbol{p_2},\cdots,\boldsymbol{p_n}$，那么如下矩阵：

$P=(\boldsymbol{p_1},\boldsymbol{p_2},\cdots,\boldsymbol{p_n})$

可以使得：

$A=P\Lambda P^{-1}$

其中$\Lambda$为如下对角阵

$\Lambda=\left(\begin{array}{llll}\lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots & \\ & & & \lambda_{n}\end{array}\right)$

其中的$\lambda_1,\lambda_2,\cdots,\lambda_n$为特征向量$\boldsymbol{p_1},\boldsymbol{p_2},\cdots,\boldsymbol{p_n}$对应的特征值，该过程称为对角化

证明过程

具体证明如下：

已知：

$P=(\boldsymbol{p_1},\boldsymbol{p_2},\cdots,\boldsymbol{p_n})$

根据矩阵乘法列观点、矩阵乘法的定义以及特征值和特征向量的定义($AP=\lambda P$)，可得：

$\begin{aligned} AP &=A(\boldsymbol{p_1},\boldsymbol{p_2},\cdots,\boldsymbol{p_n})=(A\boldsymbol{p_1},A\boldsymbol{p_2},\cdots,A\boldsymbol{p_n})\\\\ &=(\lambda_1\boldsymbol{p_1},\lambda_2\boldsymbol{p_2},\cdots,\lambda_n\boldsymbol{p_n})\\\\ &=(\boldsymbol{p_1},\boldsymbol{p_2},\cdots,\boldsymbol{p_n})\left(\begin{array}{llll}\lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots & \\ & & & \lambda_{n}\end{array}\right)\\ \end{aligned}$

令$\Lambda=\left(\begin{array}{llll}\lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots & \\ & & & \lambda_{n}\end{array}\right)$，上式可以改写为：

$AP=P\Lambda$

因为特征向量$\boldsymbol{p_1},\boldsymbol{p_2},\cdots,\boldsymbol{p_n}$线性无关，所以$P$是可逆的，因此可以给上式两侧同时右乘逆矩阵$P^{-1}$，得：

$A=P\Lambda P^{-1}$

相似对角化之后，$A^n=P\Lambda^{n}P^{-1}$，这是一个显然的结论，比如$A^2=(P\Lambda P^{-1})(P\Lambda P^{-1})$，中间可以消掉，所以是$A^2=P\Lambda^{2}P^{-1}$，依次类推，所以可以得出这个结论

所以具体步骤是

求出矩阵$A$的特征值和特征向量，如果特征值不等，就可以完成对角化
根据特征向量构造特征矩阵，对角阵$\Lambda$的对角线元素由$\lambda $构成

对角阵并不唯一，通过$A^n=P\Lambda^{n}P^{-1}$可以轻松求解矩阵高次幂

相似矩阵中的不变量

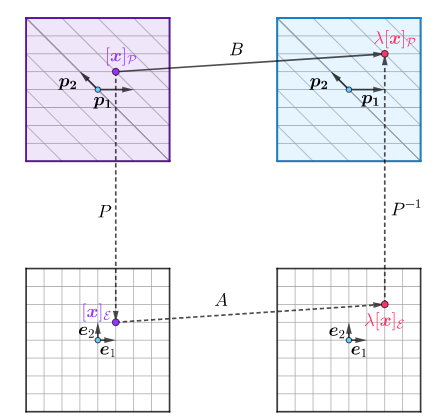
如果$A$和$B$是相似矩阵，那么，两者的特征值相同：

$A\simeq B\implies A,B的特征值相同$

证明过程

证明如下：

因为$A$和$B$是相似矩阵，所以有：

$B=P^{-1}AP$

那么结合上特征值和特征向量的定义，可以推出：

$\begin{aligned} B\boldsymbol{x}=\lambda\boldsymbol{x} &\implies P^{-1}AP\boldsymbol{x}=\lambda\boldsymbol{x}\\ &\implies AP\boldsymbol{x}=P\lambda\boldsymbol{x}\\ &\implies A(P\boldsymbol{x})=\lambda(P\boldsymbol{x}) \end{aligned}$

令$P\boldsymbol{x}=\boldsymbol{x’}$，可得：

$B\boldsymbol{x}=\lambda\boldsymbol{x},\quad A\boldsymbol{x'}=\lambda\boldsymbol{x'}$

对比可知，$A$和$B$的特征值相同，但特征向量不同。但是：两个相似矩阵对应于同一个特征值的特征向量的个数是相等的

那么通过相似矩阵将其变换为基$\mathcal{P}$下的矩阵函数$B=P^{-1}AP$，对该向量的拉伸依然是$\lambda$倍，也就是说特征值保持不变：

性质

如果$A$和$B$是相似矩阵，那么两者的行列式相同：

$\boldsymbol{A}\simeq \boldsymbol{B}\implies |\boldsymbol{A}|=|\boldsymbol{B}|$

证明过程

证明如下：

因为$\boldsymbol{A}$和$\boldsymbol{B}$是相似矩阵，所以有：

$\boldsymbol{B}=\boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P}$

两侧取行列式，结合行列式的运算性质$|\boldsymbol{A}\boldsymbol{B}|=|\boldsymbol{A}||\boldsymbol{B}|$以及$|\boldsymbol{P}^{-1}|=\frac{1}{|\boldsymbol{P}|}$，有：

$|\boldsymbol{B}|=|\boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P}|=|\boldsymbol{P}^{-1}||\boldsymbol{A}||\boldsymbol{P}|=|\boldsymbol{A}|$

实际上就是基的变化并不会影响到面积的改变

相似矩阵的迹相同
相似矩阵有相同的秩

对于$n$阶方阵$\boldsymbol{A}$，其主对角线（从左上方至右下方的对角线）的元素之和称为迹，记作$tr(\boldsymbol{A})$：

若$\lambda_1,\lambda_2,\cdots,\lambda_n$为$n$阶方阵$\boldsymbol{\boldsymbol{A}}$的特征值，则：

$tr(\boldsymbol{A})=\lambda_{1}+\lambda_{2}+\cdots+\lambda_{n}$

若$\boldsymbol{A}$和$\boldsymbol{B}$是相似矩阵，则两者的迹相同。即：

$\boldsymbol{A}\simeq\boldsymbol{B}\implies tr(\boldsymbol{A})=tr(\boldsymbol{B})$

(反过来不一定成立)

判断矩阵相似

判定矩阵之迹 (相似矩阵的迹相同)
判定矩阵之秩（判定行列式是否为0）
判定特征值（求解特征值，相似矩阵的特征值相同）
判定对于同一个特征值，特征向量的个数是否相同，比如说特征值是3,2,2，那么特征值3就有两重根，则$\lambda=3$有两个线性无关的特征向量，说明$(\lambda E-A)x=0$有2个线性无关的解，则$Rank(\lambda E-A)=n-2$

只能符合这4个条件，才能判定是矩阵相似，特征值相同≠相似

正交基与正交矩阵

正交基

已知$\boldsymbol{p}_1,\boldsymbol{p}_2,\cdots,\boldsymbol{p}_r$是向量空间$V$的一个基，如果两两正交，即满足：

$\boldsymbol{p}_i\cdot\boldsymbol{p}_j=0,\quad i\ne j$

那么称其为正交基，如果还满足长度均为1，即:

$\boldsymbol{p}_1\cdot\boldsymbol{p}_1=\boldsymbol{p}_2\cdot\boldsymbol{p}_2=\cdots=\boldsymbol{p}_r\cdot\boldsymbol{p}_r=1$

那么，就称为标准正交基

如果基为正交基，那么求其正交基下的坐标就会变得很简单：

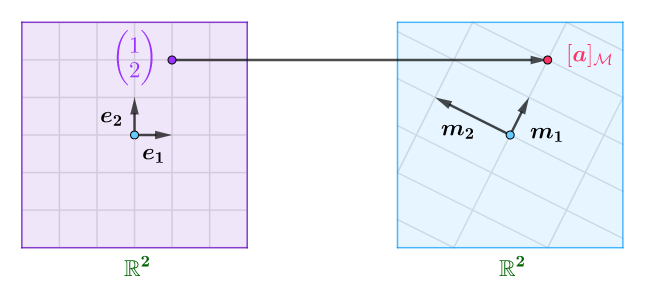
正交基：

$\mathcal{M}:\boldsymbol{m_1}=\begin{pmatrix}\displaystyle\frac{1}{2}\\1\end{pmatrix},\quad\boldsymbol{m_2}=\begin{pmatrix}-2\\1\end{pmatrix}$

并且已知向量在自然基下的坐标是$[\boldsymbol{a}]_\mathcal{E}=\begin{pmatrix}1\\2\end{pmatrix}$，求其在正交基下的坐标

本题当然可以用坐标变换公式求出，但是，因为是正交基下的特性，所以还要更简单的方法

根据坐标的定义有：

$\boldsymbol{a}=\begin{pmatrix}1\\2\end{pmatrix}=k_1\boldsymbol{m_1}+k_2\boldsymbol{m_2}$

而$m_1$和$m_2$都是正交基，所以可以：

$\boldsymbol{a}\cdot\boldsymbol{m_1}=(k_1\boldsymbol{m_1}+k_2\boldsymbol{m_2})\cdot\boldsymbol{m_1}=k_1\boldsymbol{m_1}\cdot\boldsymbol{m_1}$

根据上式可推出：

$k_1=\frac{\boldsymbol{a}\cdot\boldsymbol{m_1}}{\boldsymbol{m_1}\cdot\boldsymbol{m_1}}=\frac{1\cdot \displaystyle\frac{1}{2}+2\cdot 1}{\displaystyle\frac{1}{2}\cdot\frac{1}{2}+1\cdot 1}=2$

同样的道理，有：

$k_2=\frac{\boldsymbol{a}\cdot\boldsymbol{m_2}}{\boldsymbol{m_2}\cdot\boldsymbol{m_2}}=\frac{1\cdot (-2)+2\cdot 1}{(-2)\cdot(-2)+1\cdot 1}=0$

所以可以直接算出，坐标为

$[\boldsymbol{a}]_\mathcal{M}=\begin{pmatrix}2\\0\end{pmatrix}$

正交矩阵

假设$\boldsymbol{p}_1,\boldsymbol{p}_2,\cdots,\boldsymbol{p}_n$是向量空间$\mathbb{R}^n$的一个标准正交基，那么由它们构造的$n$阶方阵$P$也称为正交矩阵（Orthogonal Matrix）：

$P=(\boldsymbol{p}_1,\boldsymbol{p_2},\cdots,\boldsymbol{p}_n)$

该方阵$P$必然满足：

$P^\mathrm{T}P=P^{-1}P=E$

即$P^\mathrm{T}$就是$P$的逆矩阵。

证明过程

证明如下：

根据矩阵乘法的定义有

$\begin{aligned} P^\mathrm{T}P &=\begin{pmatrix}\boldsymbol{p}_1^\mathrm{T}\\\boldsymbol{p}_2^\mathrm{T} \\ \vdots \\\boldsymbol{p}_n^\mathrm{T}\end{pmatrix}(\boldsymbol{p}_1,\boldsymbol{p}_2\cdots \boldsymbol{p}_n)= \begin{pmatrix} \boldsymbol{p}_1^\mathrm{T}\boldsymbol{p}_1&\boldsymbol{p}_1^\mathrm{T}\boldsymbol{p}_2&\cdots&\boldsymbol{p}_1^\mathrm{T}\boldsymbol{p}_n\\ \boldsymbol{p}_2^\mathrm{T}\boldsymbol{p}_1&\boldsymbol{p}_2^\mathrm{T}\boldsymbol{p}_2&\cdots&\boldsymbol{p}_2^\mathrm{T}\boldsymbol{p}_n\\ \vdots&\vdots&\ddots&\vdots\\ \boldsymbol{p}_n^\mathrm{T}\boldsymbol{p}_1&\boldsymbol{p}_n^\mathrm{T}\boldsymbol{p}_2&\cdots&\boldsymbol{p}_n^\mathrm{T}\boldsymbol{p}_n\\ \end{pmatrix} \end{aligned}$

根据矩阵的转置运算的性质可知，其中$\boldsymbol{p}_i^\mathrm{T}\boldsymbol{p}_j=\boldsymbol{p}_i\cdot\boldsymbol{p}_j$，所以上式可以改写为：

$P^\mathrm{T}P= \begin{pmatrix} \boldsymbol{p}_1\cdot\boldsymbol{p}_1&\boldsymbol{p}_1\cdot\boldsymbol{p}_2&\cdots&\boldsymbol{p}_1\cdot\boldsymbol{p}_n\\ \boldsymbol{p}_2\cdot\boldsymbol{p}_1&\boldsymbol{p}_2\cdot\boldsymbol{p}_2&\cdots&\boldsymbol{p}_2\cdot\boldsymbol{p}_n\\ \vdots&\vdots&\ddots&\vdots\\ \boldsymbol{p}_n\cdot\boldsymbol{p}_1&\boldsymbol{p}_n\cdot\boldsymbol{p}_2&\cdots&\boldsymbol{p}_n\cdot\boldsymbol{p}_n\\ \end{pmatrix}$

因为标准正交基满足：

$\boldsymbol{p}_i\cdot\boldsymbol{p}_j=\begin{cases}1& &i=j\\0& &i\neq j\end{cases}$$

所以：

$\boldsymbol{P}^\mathrm{T}\boldsymbol{P} =\begin{pmatrix} \boldsymbol{p}_1\cdot\boldsymbol{p}_1&\boldsymbol{p}_1\cdot\boldsymbol{p}_2&\cdots&\boldsymbol{p}_1\cdot\boldsymbol{p}_n\\ \boldsymbol{p}_2\cdot\boldsymbol{p}_1&\boldsymbol{p}_2\cdot\boldsymbol{p}_2&\cdots&\boldsymbol{p}_1\cdot\boldsymbol{p}_n\\ \vdots&\vdots&\ddots&\vdots\\ \boldsymbol{p}_n\cdot\boldsymbol{p}_1&\boldsymbol{p}_n\cdot\boldsymbol{p}_2&\cdots&\boldsymbol{p}_n\cdot\boldsymbol{p}_n\\ \end{pmatrix} =\begin{pmatrix} 1&0&\cdots&0\\ 0&1&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&1\\ \end{pmatrix} =\boldsymbol{E}$

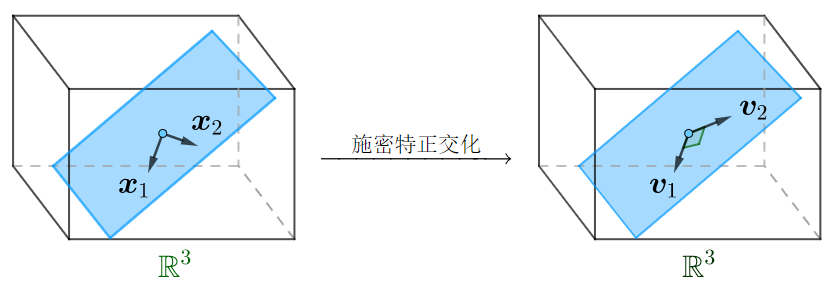
施密特正交化

正交矩阵的逆矩阵很容易求出(因为转置矩阵就是其逆矩阵)，如果在对角化中将用转置矩阵代替逆矩阵，那么可以大大降低对角化的求解难度：

$\boldsymbol{A}=\boldsymbol{P}\boldsymbol{\Lambda}\boldsymbol{P}^{-1}=\boldsymbol{P}\boldsymbol{\Lambda}\boldsymbol{P}^{\mathrm{T}}$

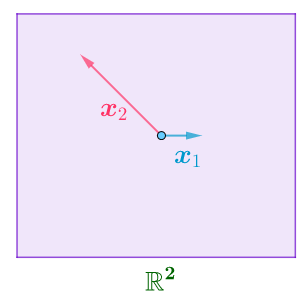
而构建正交矩阵的关键在于找到正交基，$R^2$和$R^3$的正交基很好找，就是各自的自然基，但是要寻找$R^3$中的平面的正交基，就需要利用到施密特正交化，此方法简单来说，就是借助该向量空间的一个基$\boldsymbol{x}_1,\boldsymbol{x}_2$，找到同一个向量空间的一个正交基$\boldsymbol{v}_1,\boldsymbol{v}_2：$

假设在二维空间中找到正交基

先确定一个向量作为标准基，比如说$x_1$，再作出$\boldsymbol{x_2}$在$\boldsymbol{v_1}$所在直线的投影向量$\overline{\boldsymbol{x_2}}$，连接$\boldsymbol{x_2}$和$\overline{\boldsymbol{x_2}}$就得到要求的垂线向量$\boldsymbol{v_2}$：

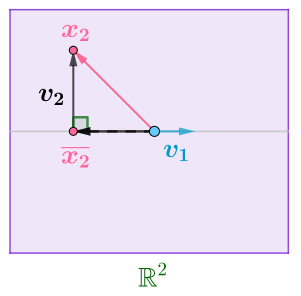
在这个过程中：

$\boldsymbol{v_2}=\boldsymbol{x_2}-\overline{\boldsymbol{x_2}}=\boldsymbol{x_2}-k_1\boldsymbol{v_1}$

因为$\boldsymbol{v_2}$和$\boldsymbol{v_1}$正交，所以：

$\begin{aligned} \boldsymbol{v_2}\cdot\boldsymbol{v_1}=0 &\implies (\boldsymbol{x_2}-k_1\boldsymbol{v_1})\cdot\boldsymbol{v_1}=0\\ &\implies \boldsymbol{x_2}\cdot\boldsymbol{v_1}-k_1\boldsymbol{v_1}\cdot\boldsymbol{v_1}=0\\ &\implies k_1=\frac{\boldsymbol{x_2}\cdot\boldsymbol{v_1}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}} \end{aligned}$

所以：

$\boldsymbol{v_2}=\boldsymbol{x_2}-k_1\boldsymbol{v_1}=\boldsymbol{x_2}-\frac{\boldsymbol{x_2}\cdot\boldsymbol{v_1}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1}$

这样就得到了一组正交基$\boldsymbol{v}_1,\boldsymbol{v}_2$

总结如下：

$\boldsymbol{x_1},\boldsymbol{x_2} \xrightarrow{\quad\text{施密特正交化}\quad} \begin{cases} \boldsymbol{v_1}=\boldsymbol{x_1}\\ \quad\\ \boldsymbol{v_2}=\boldsymbol{x_2}-\frac{\boldsymbol{x_2}\cdot\boldsymbol{v_1}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1} \end{cases}$

在三维空间中，就是：

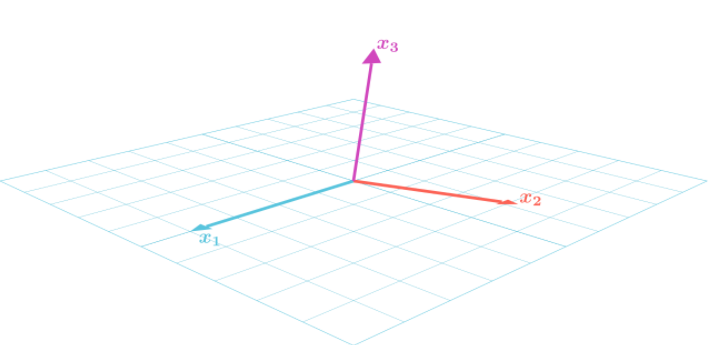
先将其中两个向量施密特正交化：

作出$\boldsymbol{x_3}$在$\boldsymbol{v_1},\boldsymbol{v_2}$张成平面上的投影向量$\overline{\boldsymbol{x_3}}$，连接$\boldsymbol{x_3}$和$\overline{\boldsymbol{x_3}}$就得到要求的垂线向量$\boldsymbol{v_3}$：

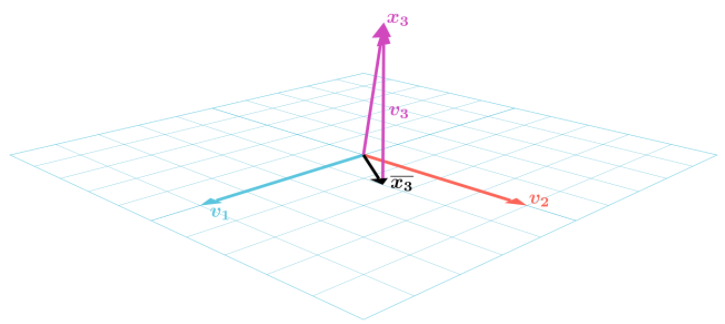
求出：

$\boldsymbol{v_3}=\boldsymbol{x_3}-\frac{\boldsymbol{x_3}\cdot\boldsymbol{v_1}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1}-\frac{\boldsymbol{x_3}\cdot\boldsymbol{v_2}}{\boldsymbol{v_2}\cdot\boldsymbol{v_2}}\boldsymbol{v_2}$ $\boldsymbol{x_1},\boldsymbol{x_2},\boldsymbol{x_3} \xrightarrow{\quad\text{施密特正交化}\quad} \begin{cases} \boldsymbol{v_1}=\boldsymbol{x_1}\\ \quad\\ \boldsymbol{v_2}=\boldsymbol{x_2}-\frac{\boldsymbol{x_2}\cdot\boldsymbol{v_1}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1}\\ \quad\\ \boldsymbol{v_3}=\boldsymbol{x_3}-\frac{\boldsymbol{x_3}\cdot\boldsymbol{v_1}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1}-\frac{\boldsymbol{x_3}\cdot\boldsymbol{v_2}}{\boldsymbol{v_2}\cdot\boldsymbol{v_2}}\boldsymbol{v_2} \end{cases}$

这种方法就是施密特正交法

正交对角化

已知对角化的过程是：

$A=P\Lambda P^{-1}$

需要求逆矩阵，很复杂，而通过正交矩阵可以轻松求逆矩阵：

$A=P\Lambda P^{\mathrm{-1}}=P\Lambda P^{\mathrm{T}}$

正交基构成了正交矩阵，但是，不是在标准空间里面的话，就需要用施密特正交化来求其正交基，继而求得求正交矩阵。

以上一整个过程叫做正交对角化

实对称阵

如果矩阵$A$是对称阵(即其转置是其本身的矩阵)，且其中的每一个元素都是实数，那么称之为实对称阵。此时有如下性质：

若$\lambda_1,\lambda_2$是实对称阵$A$相异的特征值，$\boldsymbol{p}_1,\boldsymbol{p}_2$是$\lambda_1,\lambda_2$对应的特征向量，则有$\boldsymbol{p}_1$与$\boldsymbol{p}_2$正交，即：

$\boldsymbol{p_1}\cdot\boldsymbol{p_2}=0$

根据上述性质就可以找到标准正交基中的第一个向量$\boldsymbol{\epsilon_1}$

并不是所有的矩阵都能完成正交对角化，只有实对称阵才行

找到第一个向量后，根据实对称阵的性质，将其作为基，与其他的特征向量是正交的

之后用施密特正交化其他的向量，使其正交，再单位化即可

来道经典例题：

已知$A$是三阶实对称矩阵，若正交矩阵$Q$使得$Q^{-1}AQ=\begin{pmatrix}3&0&0\\0&3&0\\0&0&6\end{pmatrix}$，如果$a_1=(1,0,-1)^{T},a_2=(0,1,1)^{T}$是矩阵$A$属于特征值$\lambda=3$的特征向量，则$Q$是多少？

如果已知两个特征向量，那么根据实对称矩阵的性质，可以求出第三个特征向量，再拓展一下，即使只知道一个特征向量$a_1$，如果另外两个特征向量对应的特征值相等，那么可以根据$a_2×a_1=0,a_3×a_1=0$，通过基础解系解出$a_2$和$a_3$

解：已知实对称矩阵不同特征值两两正交，所以可以解出$a_3$

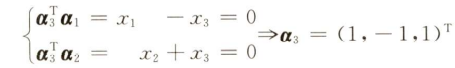
因为$a_1,a_2$不正交，所以要用施密特正交化处理

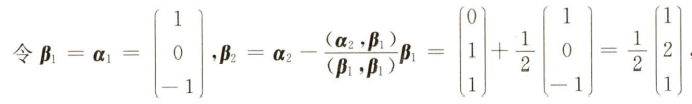
将处理后的向量单位化

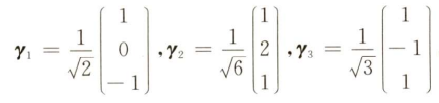
组合起来即是$Q$

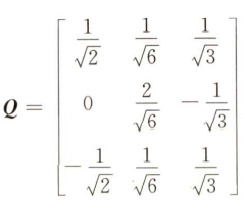
正交变换中求正交矩阵的方法一共有2种，如下：

利用特征值算出特征向量，如果特征值各不相同，只需要将各个特征向量单位化，组成的矩阵即是正交矩阵，如果特征值有相同的，则需要进行施密特正交化，然后再组成正交矩阵
直接利用拉格朗日配方法，写出$x$到$y$的变化的关系式，可以根据$x$到$y$的关系的相关系数，直接得到正交矩阵

二次型

在数学中，关于一些变量的二次齐次多项式被称为二次型（Quadratic form）

$3x_1^2-7x_2^2,\quad 3x_1^2+2x_2^2+4x_1x_2,\quad x_1^2+4x_3^2+x_1x_2$

$f$是一个定义在$\mathbb{R}^n$上的二次型，它可改写为：

$f=\boldsymbol{x}^T\boldsymbol{A}\boldsymbol{x}$

其中$\boldsymbol{A}$是$n\times n$的对称阵，该矩阵$\boldsymbol{A}$称为$f$的二次型矩阵

二次型到矩阵

判断矩阵的大小，应该为$n$阶方阵，$n$为变量的个数

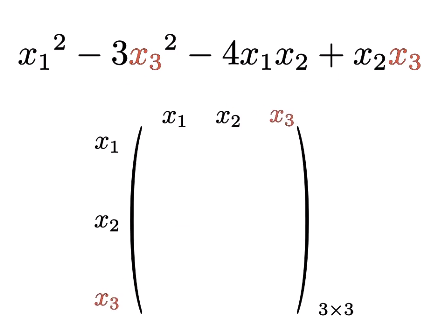
将二次型的平方项保留，交叉项平分

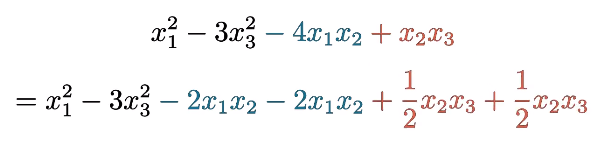
平方项的系数自然是对角线上的数，而交叉项的系数是根据其下标交叉的值

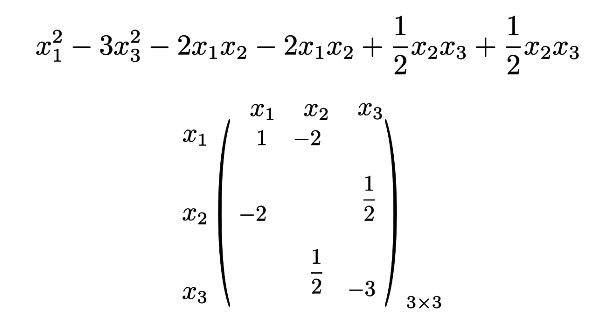
剩下的位置置0

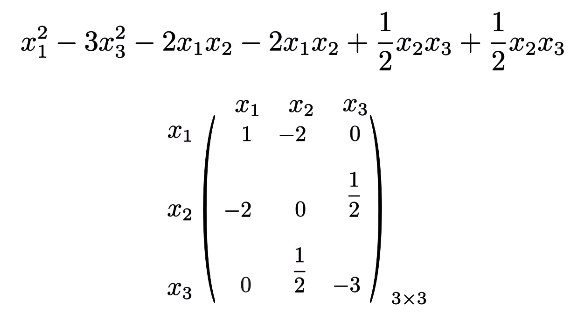
这样就完成了从二次型到矩阵，而从矩阵到二次型，只需要将过程反过来就行了

合同矩阵

定义：设$\boldsymbol{A}和\boldsymbol{B}$是$n$阶方阵，若有可逆矩阵$\boldsymbol{P}$，使$\boldsymbol{B}=\boldsymbol{P}^\mathrm{T}\boldsymbol{A}\boldsymbol{P}$，则称矩阵$\boldsymbol{A}$和$\boldsymbol{B}$合同，或者称$\boldsymbol{B}$是$\boldsymbol{A}$的合同矩阵

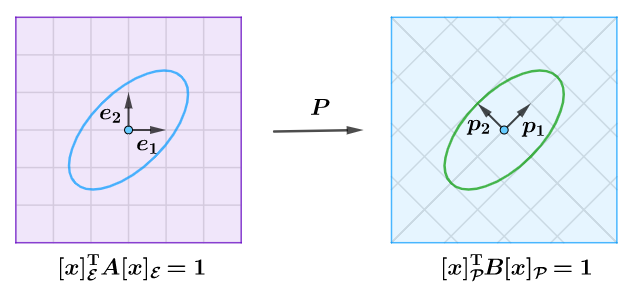
合同矩阵适用于曲线的旋转，符合转置矩阵的意义

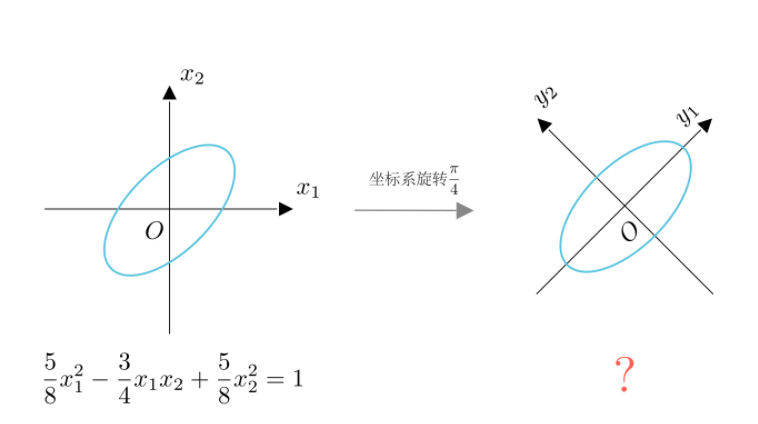
本题可通过三个步骤完成：

（1）将椭圆改写为$[\boldsymbol{x}]_\mathcal{E}^\mathrm{T}\boldsymbol{A}[\boldsymbol{x}]_\mathcal{E}=1$，得到其在自然基$\mathcal{E}$下的方程；

（2）利用合同矩阵，得到基$\mathcal{P}$下的椭圆方程$[\boldsymbol{x}]_\mathcal{P}^\mathrm{T}\boldsymbol{B}[\boldsymbol{x}]_\mathcal{P}=1；$

（3）将基$\mathcal{P}$下的方程$[\boldsymbol{x}]_\mathcal{P}^\mathrm{T}\boldsymbol{B}[\boldsymbol{x}]_\mathcal{P}=1$写回一般形式即可。

条件

矩阵合同的条件是：两个矩阵的正，负惯性系数相同

如果$A$是实对称矩阵，那么和$A$合同的矩阵也是实对称矩阵

标准形和合同对角化

判断二次型的曲线类型，可以通过合同对角化判断

标准形：只含平方项的二次型

$k_1x_1^2+k_2x_2^2+\cdots+k_nx_n^2$

称为二次型的标准形，或者简称为标准形。其二次型矩阵一定为$n$阶对角阵：

$\boldsymbol{\Lambda}= \begin{pmatrix} k_1&0&\cdots&0\\ 0&k_2&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&k_n \end{pmatrix}$

合同矩阵只是对二次型进行坐标变换，并不会改变曲线类型，所以可借助合同矩阵来去掉交叉项。过程如下：

$x_1x_2=1\xrightarrow{\quad 改写 \quad}\boldsymbol{x}^\mathrm{T}\boldsymbol{A}\boldsymbol{x}=1\xrightarrow{\quad合同矩阵\quad}\boldsymbol{A}=\boldsymbol{P}^\mathrm{T}\boldsymbol{\Lambda}\boldsymbol{P}\xrightarrow{\quad去除交叉项\quad}\boldsymbol{y}^\mathrm{T}\boldsymbol{\Lambda}\boldsymbol{y}=1$

比如判断$x_1x_2=1$的曲线类型：

改写。根据二次型矩阵的构造方法，方程$x_1x_2=1$中的$x_1x_2$对应的二次型矩阵为：

$\boldsymbol{A}=\begin{pmatrix}0&\displaystyle\frac{1}{2}\\\displaystyle\frac{1}{2}&0\end{pmatrix}$

令$\boldsymbol{x}=\begin{pmatrix}x_1\\x_2\end{pmatrix}$，那么方程$x_1x_2=1$可改写为：

$x_1x_2=\begin{pmatrix}x_1&x_2\end{pmatrix}\begin{pmatrix}0&\displaystyle\frac{1}{2}\\\displaystyle\frac{1}{2}&0\end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}=\boldsymbol{x}^\mathrm{T}\boldsymbol{A}\boldsymbol{x}=1$

通过合同矩阵，将$\boldsymbol{A}$化为对角阵$\boldsymbol{\Lambda}$。该二次型矩阵$\boldsymbol{A}$是实对称阵，所以必然可正交对角化，从而得到$\boldsymbol{A}$的合同矩阵$\boldsymbol{\Lambda}$：

$\begin{aligned} \boldsymbol{A} &=\begin{pmatrix}0&\displaystyle\frac{1}{2}\\\displaystyle\frac{1}{2}&0\end{pmatrix}=\boldsymbol{P}\boldsymbol{\Lambda}\boldsymbol{P}^{-1}=\boldsymbol{P}\boldsymbol{\Lambda}\boldsymbol{P}^\mathrm{T}\\ &=\begin{pmatrix}\displaystyle\frac{\sqrt{2}}{2}&-\displaystyle\frac{\sqrt{2}}{2}\\\displaystyle\frac{\sqrt{2}}{2}&\displaystyle\frac{\sqrt{2}}{2}\end{pmatrix}\begin{pmatrix}\displaystyle\frac{1}{2}&0\\0&-\displaystyle\frac{1}{2}\end{pmatrix}\begin{pmatrix}\displaystyle\frac{\sqrt{2}}{2}&\displaystyle\frac{\sqrt{2}}{2}\\-\displaystyle\frac{\sqrt{2}}{2}&\displaystyle\frac{\sqrt{2}}{2}\end{pmatrix} \end{aligned}$

其中$\boldsymbol{P}=\begin{pmatrix}\displaystyle\frac{\sqrt{2}}{2}&-\displaystyle\frac{\sqrt{2}}{2}\\\displaystyle\frac{\sqrt{2}}{2}&\displaystyle\frac{\sqrt{2}}{2}\end{pmatrix}$是正交矩阵，有$\boldsymbol{P}^{-1}=\boldsymbol{P}^\mathrm{T}。$

去除交叉项。因为$\boldsymbol{A}=\boldsymbol{P}\boldsymbol{\Lambda}\boldsymbol{P}^\mathrm{T}$，所以：

$\boldsymbol{x}^\mathrm{T}\boldsymbol{A}\boldsymbol{x}= \boldsymbol{x}^\mathrm{T}\boldsymbol{P}\boldsymbol{\Lambda}\boldsymbol{P}^\mathrm{T}\boldsymbol{x}=(\boldsymbol{P}^\mathrm{T}\boldsymbol{x})^\mathrm{T}\boldsymbol{\Lambda}(\boldsymbol{P}^\mathrm{T}\boldsymbol{x})$

令$\boldsymbol{y}=\boldsymbol{P^\mathrm{T}}\boldsymbol{x}=\begin{pmatrix}y_1\\y_2\end{pmatrix}$，则：

$(\boldsymbol{P}^\mathrm{T}\boldsymbol{x})^\mathrm{T}\boldsymbol{\Lambda}(\boldsymbol{P}^\mathrm{T}\boldsymbol{x})=1\implies \boldsymbol{y}^\mathrm{T}\boldsymbol{\Lambda}\boldsymbol{y}=1\implies \frac{1}{2}y_1^2-\frac{1}{2}y_2^2=1$

因为是$x_1x_2=1$通过合同矩阵得到的去除交叉项后的$\frac{1}{2}y_1^2-\frac{1}{2}y_2^2=1$，所以两者对应的其实是同一个曲线，曲线类型没有发生变化。$\frac{1}{2}y_1^2-\frac{1}{2}y_2^2=1$的系数为一正一负，所以是双曲线，从而$x_1x_2=1$是双曲线。

这种方法叫做正交合同对角化

实际上，其实对于任意的二次型, 为求得其标准型, 我们所需要做的就是求得二次型矩阵的特征值，并不需要求其正交矩阵

由于对角阵并不唯一，所以标准型也不唯一，但是标准型的正，负惯性系数肯定是相同的

拉格朗日配方法

具体步骤为：

遇到二次型中的平方项$x_i^2$，就把含有$x_i$的项集中起来，然后配方；
遇到$x_ix_j$，且没有平方项$x_i^2或x_j^2$，则进行函数换元：

$\begin{cases} x_i=y_i+y_j\\ x_j=y_i-y_j\\ x_k=y_k(k=1,2,\cdots,n,\quad k\neq i,j) \end{cases}$

上述操作会产生平方项，再回到（1）去尝试配方；

不断重复（1）、（2），直至消去所有的交叉项。

例请通过拉格朗日配方法来判断$x_1x_2=1$的曲线类型。
解（1）完成拉格朗日配方法。首先对$x_1x_2$进行函数换元：

$\begin{cases} x_1=y_1+y_2\\ x_2=y_1-y_2 \end{cases}$

则：

$x_1x_2=(y_1+y_2)(y_1-y_2)=y_1^2-y_2^2$

这样就得到了$x_1x_2$的不同的标准形

$x_1x_2\quad\xrightarrow{\quad\large 拉格朗日配方法\quad}y_1^2-y_2^2$

只能适用于实对称矩阵的的秩为满秩的情况，拉格朗日正交法的本质是坐标变换，如果矩阵不满秩，自然不能进行坐标变换

可以通过配方法来快速求出合同矩阵$P$，比如二次型$2x_1x_3+x_2^2$，令

$\begin{cases} x_1=y_1+y_3\\ x_2=y_2\\ x_3=y_1-y_3 \end{cases}$

可以拆成是$2y_1+y_3(y_1-y_3)+y_2^2=2y_1^2+y_2^2-2y_3^2$，化为标准型，根据$x=Cy$，可以得出$C$的形式

$\begin{pmatrix}1&0&1\\0&1&0\\1&0&-1\end{pmatrix}$

当然这个矩阵不唯一

惯性定理

对于某二次型$f$，通过合同对角化可化为多个标准形。这些标准形共同的特点为，其正系数的数目（也称为正惯性指数）、负系数的数目（也称为负惯性指数）以及 0 系数的数目都相同。该定理称为西尔维斯特惯性定理，简称惯性定理。

设二次型$f(\boldsymbol{x})=\boldsymbol{x}^TA\boldsymbol{x}$，则它是：

正定的，如果对所有$\boldsymbol{x}\neq \boldsymbol{0}$，有$f(\boldsymbol{x}) > 0$
半正定的，如果始终有$f(\boldsymbol{x}) \geq 0$
负定的，如果对所有$\boldsymbol{x}\neq \boldsymbol{0}$，有$f(\boldsymbol{x}) < 0$
半负定的，如果始终有$f(\boldsymbol{x}) \leq 0$
不定的，如果$f(\boldsymbol{x})$既有正值又有负值

判断正定矩阵的方法：

已知二次型$f(\boldsymbol{x})=\boldsymbol{x}^T\boldsymbol{A}\boldsymbol{x}$，其为正定的充分必要条件是，$\boldsymbol{A}$的各阶顺序主子式都为正，等同于正惯性系数$p=n$，即：

$a_{11} > 0,\quad \begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix} > 0,\cdots, \begin{vmatrix}a_{11}&\cdots&a_{1n}\\ \vdots&&\vdots\\a_{n1}&\cdots&a_{nn}\end{vmatrix} > 0$

为负定的充分必要条件是，奇数阶顺序主子式为负，而偶数阶顺序主子式为正，即:

$(-1)^r\begin{vmatrix}a_{11}&\cdots&a_{1r}\\ \vdots&\quad&\vdots\\a_{r1}&\cdots&a_{rr}\end{vmatrix} > 0 \quad (r=1,2,\cdots,n)$

这个定理称为赫尔维茨定理

正定的必要条件：$a_{ii}>0$，特征值都＞0

求正惯性系数的方法：

方法1：对应的对称矩阵的正特征值的个数(重根算一个)

方法2：将二次型通过拉格朗日配方法转换为标准形

正惯性系数+负惯性系数=矩阵的秩

设$x=(x_1,x_2,x_3)^T$，求$x^Tx=1$时，$x^TAx$的最大值

在已知$A$特征值的情况下，存在正交矩阵$P$,经正交变换$x=Py$化二次型$x^TAx$为标准型

$y^Ty=y^TP^TPy=(Py)^T(Py)=x^Tx=1$ $x^TAx=\lambda_1 y_1^2+\lambda _2y_2^2+\lambda _3y_3^2≤max[\lambda_1,\lambda_2,\lambda_3](y_1^2+y_2^2+y_3^2)=max[\lambda_1,\lambda_2,\lambda_3]$

$(y_1^2+y_2^2+y_3^2)=1$因为模长为1，结论很好理解，因为$(y_1^2+y_2^2+y_3^2)=1$，所以让$max[\lambda]$之后的那个$y=1$即是最大值