矩阵函数

定义

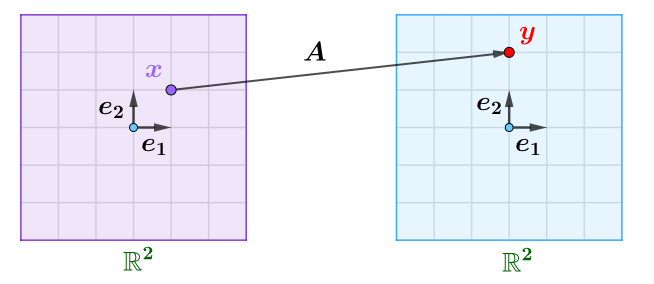
如果将矩阵左乘$Aa=b$中的常向量$a$，$b$变为位置向量$x$，$y$，就得到了矩阵函数$Ax=y$

相对于矩阵左乘这种运算而言，矩阵函数是更抽象、更核心的数学概念

旋转矩阵

$\boldsymbol{A}=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}$

该矩阵左乘$Aa=b$的结果是，让$b$相对$a$逆时针旋转了$\theta$，所以称该矩阵为旋转矩阵

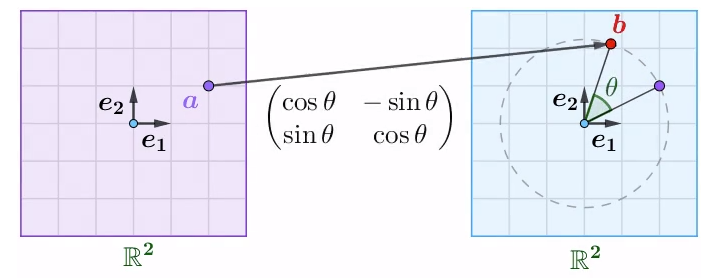
将旋转矩阵看做是

$\boldsymbol{c_1}=\begin{pmatrix}\cos\theta\\\sin\theta\end{pmatrix},\quad\boldsymbol{c_2}=\begin{pmatrix}-\sin\theta\\\cos\theta\end{pmatrix}$

两个列向量，显然$e_1×c_1$会导致$e_1$逆时针旋转，而$e_2$在$y$轴上，根据三角公式

$\begin{cases} \sin(\frac{\pi}{2}+\theta)=\cos(\theta)\\ \cos(\frac{\pi}{2}+\theta)=-\sin(\theta) \end{cases}$

所以也会逆时针旋转

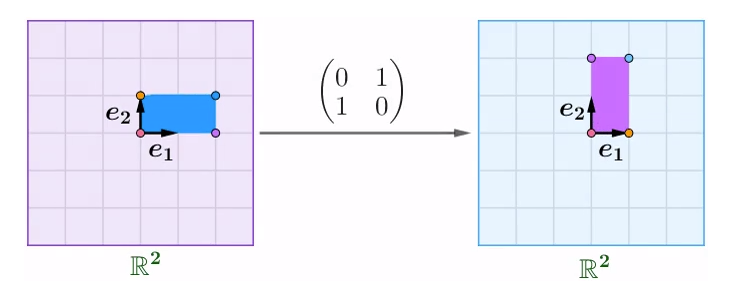
镜像矩阵

从矩阵函数的观点看初等行变化，对换变化中的二阶矩阵就是镜像矩阵

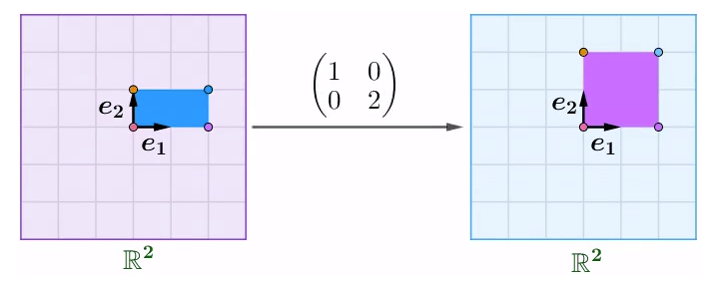
伸缩矩阵

从矩阵函数的观点看初等行变化，倍乘变化中的矩阵就是伸缩矩阵，格式为：

$\boldsymbol{A}=\begin{pmatrix}1&0\\0&k\end{pmatrix}$

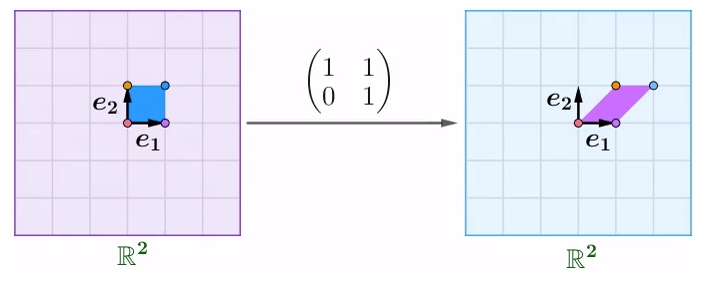
剪切矩阵

从矩阵函数的观点看初等行变化，倍加变化中的矩阵就是剪切矩阵，格式为：

$\boldsymbol{A}=\begin{pmatrix}1&k\\0&1\end{pmatrix}$

列向量为：

$\boldsymbol{c_1}=\begin{pmatrix}1\\0\end{pmatrix}=\boldsymbol{e_1},\quad\boldsymbol{c_2}=\begin{pmatrix}k\\1\end{pmatrix}=\boldsymbol{e_2}+\begin{pmatrix}k\\0\end{pmatrix}=k\boldsymbol{e_1}+\boldsymbol{e_2}$

在列向量的作用下，输出向量$y$在$e_1$方向上进行了平移

秩

定义

之前在向量一章中提到过：

虽然向量组的最大无关组并不唯一，但是最大无关组包含向量的数目是相同的，此不变的数目就称为秩（rank）

向量组的最大无关组中向量的数目就是秩，而在矩阵中，要分为列空间和行空间的秩进行讨论

包含所有列向量的向量组称为列向量组，记作$colsp(A)$，即：

$\begin{aligned} colsp(\boldsymbol{A}) &=span(\{\boldsymbol{c_1},\boldsymbol{c_2},\cdots,\boldsymbol{c_n}\})=x_1\boldsymbol{c_1}+x_2\boldsymbol{c_2}+\cdots+x_n\boldsymbol{c_n},\quad x_{1,2,\cdots,n}\in\mathbb{R} \end{aligned}$

列向量组的秩，也就是列空间的维度，称为列秩，如果列向量组线性无关，就称为列满秩

包含所有行向量的向量组称为行向量组，记作$rowsp(A)$，即：

$\begin{aligned} rowsp(\boldsymbol{A}) &=span(\{\boldsymbol{r_1}^\mathrm{T},\boldsymbol{r_2}^\mathrm{T},\cdots,\boldsymbol{r_m}^\mathrm{T}\})=x_1\boldsymbol{r_1}^\mathrm{T}+x_2\boldsymbol{r_2}^\mathrm{T}+\cdots+x_m\boldsymbol{r_m}^\mathrm{T},\quad x_{1,2,\cdots,m}\in\mathbb{R} \end{aligned}$

行向量组的秩，也就是行空间的维度，称为行秩，如果行向量组线性无关，就称为行满秩

对任意矩阵，始终有列秩等于行秩，所以统称为矩阵的秩，矩阵$A$的秩记作$rank(A)$

因为行秩=列秩=秩，所以在自然定义域下时，秩就是矩阵函数的值域的维度

$\begin{array}{c|c|c} \hline \quad \text{自然定义域}\quad&\quad \text{秩}\quad&\quad \text{值域维度}\quad \\ \hline \quad \mathbb{R}^2\quad&\quad\begin{aligned}rank(\boldsymbol{A})=2\\rank(\boldsymbol{A})=1\\ rank(\boldsymbol{A})=0\end{aligned}\quad&\quad\begin{aligned}\text{2 维}\\\text{1 维}\\\text{0 维}\end{aligned}\quad\\ \hline \end{array}$

如果某个矩阵，既是列满秩，又是行满秩，那么就称该矩阵为满秩矩阵，或者称为满秩。满秩矩阵必为方阵

$rank(AB)\leq\min\Big(rank(A),rank(B)\Big)$

两个矩阵等价$\Leftrightarrow$ 两个矩阵的秩相同

性质

秩的取值范围：
$0\le rank(A_{m\times n})\le\min(m,n)$
矩阵经过转置后，秩不变
满秩矩阵复合的秩。假设$P$、$Q$为满秩矩阵，那么：
$rank(PA)=rank(AQ)=rank(PAQ)=rank(A)$
矩阵相加的秩，假设$A$,$B$为同型矩阵，那么
$rank(A+B)\le rank(A)+rank(B)$
复合函数的秩：
$rank(AB)\leq\min\Big(rank(A),rank(B)\Big)$
如果$AB=O$，$A,B$为$n$阶矩阵，那么
$rank(A)+rank(B)≤n$

函数的四要素

定义域：集合$X$

映射法则$f$：指明$X$中的元素怎么和$Y$元素关联

值域：通过映射法则$f$和定义域$X$决定，表示$X$映射到$Y$中的值

到达域：集合$Y$

对于$m×n$的矩阵：

$\underbrace{A}_{m\times n}\quad\underbrace{\boldsymbol{x_{}}}_{n\times 1}\quad=\quad\underbrace{\boldsymbol{y_{}}}_{m\times 1}$

自然定义域为$R^n$，因为$n$维向量$\boldsymbol{x_{}}=\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}$为$R^n$中的任意向量
映射法则为矩阵$A$以及矩阵乘法的规则
值域为$Ax$
到达域为$R^m$，因为$\boldsymbol{y_{}}=\begin{pmatrix}y_1\\y_2\\\vdots\\y_m\end{pmatrix}$是$m$维向量，所以值域必然在$R_m$中

映射法则分几种情况

单射：映射法则是单的，简称单射，当且仅当每一个$y$至多有一个$x$与之对应

满射：映射法则是满的，简称满射，当且仅当每一个$y$至多有一个$x$与之对应，此时值域与到达域相等

双射：即是单射又是满射

总结：

列向量矩阵$Ax=y$的四要素

$\begin{array}{c|c|c|c} \hline \quad 自然定义域\quad&\quad 映射法则 \quad&\quad 值域 \quad&\quad 到达域 \quad\\\hline\\ \quad \mathbb{R}^n \quad&\quad \boldsymbol{A} \quad&\quad colsp(\boldsymbol{A}) \quad&\quad \mathbb{R}^m \quad\\ \\ \hline \end{array}$

行向量矩阵$x^TA=y^T$的四要素

$\begin{array}{c|c|c|c} \hline \quad 自然定义域\quad&\quad 映射法则 \quad&\quad 值域 \quad&\quad 到达域 \quad\\\hline\\ \quad \mathbb{R}^m \quad&\quad \boldsymbol{A} \quad&\quad rowsp(\boldsymbol{A}) \quad&\quad \mathbb{R}^n \quad\\ \\ \hline \end{array}$

函数的单射

定义域维度=值域维度时，才能形成单射

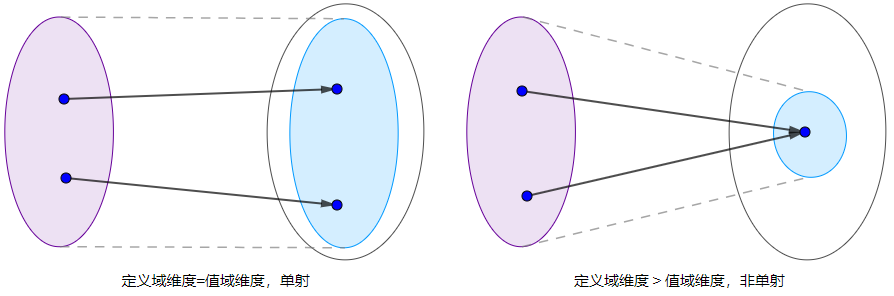
那么只要行满秩，或者列满秩的情况下，矩阵函数才会不改变函数的维度

$\begin{array}{c|c|c|c} \hline \quad矩阵函数\quad&\quad 单射的充要条件 \quad\\\hline\\ \quad \boldsymbol{A}\boldsymbol{x}=\boldsymbol{y} \quad&\quad 列满秩 \iff 单射 \quad\\ \quad \boldsymbol{x}^\mathrm{T}\boldsymbol{A}=\boldsymbol{y}^\mathrm{T} \quad&\quad 行满秩 \iff 单射\quad\\ \\ \hline \end{array}$

只有单射情况下，线性方程才有唯一解，当然也有可能无解(解在值域外，到达域中)

函数的满射

只有值域$colsp(A)$和到达域$R^m$一样时，列向量$Ax=y$才会满射

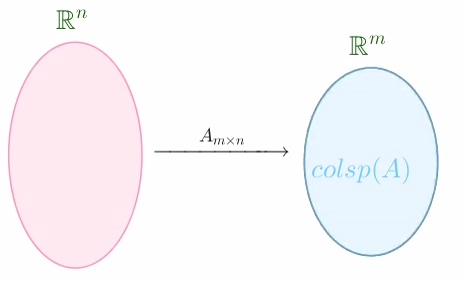
假设$A$为$m×n$的矩阵，满射时，必有$Rank(colsp(A))$=$R^m$

那么就要求，矩阵的列秩必须是$m$，而行秩=列秩，所以行秩为$m$，行满秩

所以满射条件是：

$\boldsymbol{A}\ \text{是行满秩}\iff \boldsymbol{A}\boldsymbol{x}=\boldsymbol{y}\ \text{是满射}$ $\begin{array}{c|c|c|c} \hline \quad矩阵函数\quad&\quad 满射的充要条件 \quad\\\hline\\ \quad \boldsymbol{A}\boldsymbol{x}=\boldsymbol{y} \quad&\quad 行满秩 \iff 满射 \quad\\ \quad \boldsymbol{x}^\mathrm{T}\boldsymbol{A}=\boldsymbol{y}^\mathrm{T} \quad&\quad 列满秩 \iff 满射\quad\\ \\ \hline \end{array}$

只有函数在满射的情况下，方程才有解

函数的双射

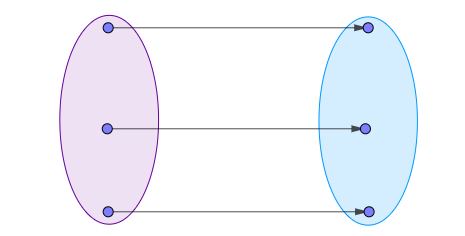
双射就是即是单射，又是满射，结合两者的成立条件：

$\begin{array}{c|c|c|c} \hline \quad矩阵函数\quad&\quad 单射的充要条件 \quad&\quad 满射的充要条件 \quad&\quad 双射的充要条件 \quad\\\hline\\ \quad \begin{aligned}A\boldsymbol{x}=\boldsymbol{y}\ \ \\\boldsymbol{x}^\mathrm{T}A=\boldsymbol{y}^\mathrm{T}\end{aligned} \quad&\quad \begin{aligned}列满秩\\行满秩\end{aligned} \quad&\quad \begin{aligned}行满秩\\列满秩\end{aligned} \quad&\quad 满秩\quad\\ \\ \hline \end{array}$

总结

单射	满射	结果
√	√	必有解，且为唯一解
√	×	有可能有解，有可能无解，若有解，必为唯一解
×	√	必然有解，解必然不唯一

秩的求法

秩很容易求出来，可以将矩阵化为行阶梯形矩阵，秩就是非零行的个数

在行最简形矩阵的基础上，再执行若干次初等行变化，就可以得到形式更简单地矩阵，特点是左上角是单位阵

$\begin{pmatrix}1&2&0\\0&0&1\\0&0&0\end{pmatrix}\xrightarrow[\color{red}{\text{倍加}}]{\quad \boldsymbol{c}_2'=-2\boldsymbol{c}_1+\boldsymbol{c}_2\quad}\begin{pmatrix}1&0&0\\0&0&1\\0&0&0\end{pmatrix}\xrightarrow[\color{red}{\text{对换}}]{\quad \boldsymbol{c}_2\leftrightarrow \boldsymbol{c}_3\quad}\begin{pmatrix}1&0&0\\0&1&0\\0&0&0\end{pmatrix}$

这种矩阵被称为标准形

实际上标准型非常好求出来，只需要判断矩阵的秩，然后再对角线上填上等于秩个数的$1$即可

逆矩阵

定义

如果函数只有单射，或只是满射，那么无法建立起逆矩阵，只有在双射情况下，矩阵才有逆矩阵

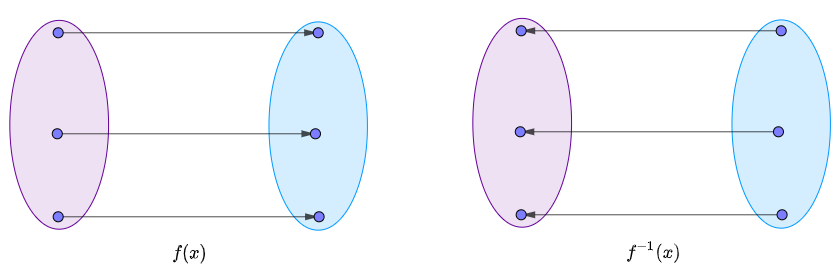
所以根据矩阵双射的条件有：

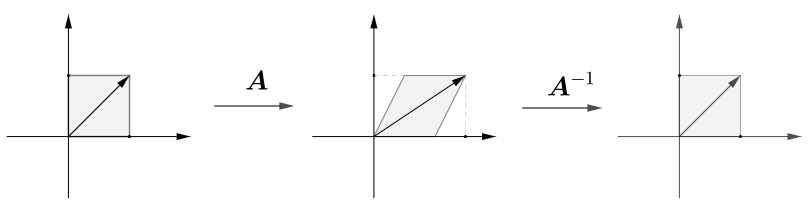
当矩阵$A$为满秩矩阵时，对应的矩阵函数为双射，此时$A$存在反函数，称为$A$可逆。其反函数记作$A^{-1}$，称为$A$的逆矩阵

之前提到过，单位阵$I$的定义如下

而对图形先运用矩阵$A$，再运用逆矩阵$A^{-1}$，图形同样不会发生变化

逆矩阵定义如下：若存在两个$n$阶矩阵$A$，$C$，两者的乘积为$n$阶单位阵$I$：

$AC=I 且CA=I$

那么$C$就是$A$的逆矩阵，即有$A^{-1}=C$，且$A^{-1}$是惟一的

求法

如果可以通过一系列初等行矩阵$E^i$，将矩阵$A$变换成单位阵$I$，则$A$的逆矩阵就是这些初等行矩阵的乘积：

$\underbrace{\boldsymbol{E}_1\boldsymbol{E}_2...\boldsymbol{E}_n}_{\boldsymbol{A}^{-1}}\boldsymbol{A}=\boldsymbol{I}$

实际上分为两步：

先通过一系列初等行矩阵，将矩阵$A$变换成单位阵$I$
然后将这些初等行矩阵相乘得到逆矩阵

联系到之前提到过的高斯消元法，可以将这两步合并在一起进行

首先将矩阵$A$和$I$合成一个矩阵$( A|I )$，然后在新矩阵$( A|I )$上运用一系列初等行矩阵。这样就可以在得到单位阵的同时，得到逆矩阵：

$( A|I )\xrightarrow{\quad E_1,E_2,...,E_n\quad }( I|A^{-1} )$

实际上这里利用分块矩阵的方法，将一个矩阵成了两块，每块都乘以$A^{-1}$

性质

若$A，B$是同阶方阵且均可逆，则$AB$也可逆，且
$(\boldsymbol{A}\boldsymbol{B})^{-1}=\boldsymbol{B}^{-1}\boldsymbol{A}^{-1}$
若$A$可逆，则$A^T$也可逆，且：
$(\boldsymbol{A}^\mathrm{T})^{-1}=(\boldsymbol{A}^{-1})^\mathrm{T}$
分块矩阵的逆矩阵：
$\begin{pmatrix}A&O\\O&B\end{pmatrix}^{-1}=\begin{pmatrix}A^{-1}&O\\O&B^{-1}\end{pmatrix}$ $\begin{pmatrix}O&A\\B&O\end{pmatrix}^{-1}=\begin{pmatrix}O&B^{-1}\\A^{-1}&O\end{pmatrix}$

分块矩阵

定义

对于行数和列数较多的矩阵$A$，运算时采用分块法，将大矩阵的运算化为小矩阵的运算

$A=\left( {\begin{array}{c|c} \overbrace{ \begin{matrix} a_{11}&\cdots&a_{1r}\\ \vdots& &\vdots\\ a_{s1}&\cdots&a_{sr}\\ \end{matrix}}^{\Large 子块A_{11}} &\overbrace{ \begin{matrix} a_{1(r+1)}&\cdots&a_{1n}\\ \vdots& &\vdots\\ a_{s(r+1)}&\cdots&a_{sn}\\ \end{matrix}}^{\Large 子块A_{12}}\\ \hline \underbrace{ \begin{matrix} a_{(s+1)1}&\cdots&a_{(s+1)r}\\ \vdots& &\vdots\\ a_{m1}&\cdots&a_{mr}\\ \end{matrix}}_{\Large 子块A_{21}} &\underbrace{ \begin{matrix} a_{(s+1)(r+1)}&\cdots&a_{(s+1)n}\\ \vdots& &\vdots\\ a_{m(r+1)}&\cdots&a_{mn}\\ \end{matrix}}_{\Large 子块A_{22}} \end{array}} \right)$

可以改写成如下形式：

$A=\begin{pmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{pmatrix}$

分块矩阵的形式多种多样，可以任意划分

运算规则

分块矩阵的运算规则和普通矩阵的几乎一样

加法：

$A+B=\begin{pmatrix}A_{11}+B_{11}&\cdots&A_{1r}+B_{1r}\\ \vdots&&\vdots\\A_{s1}+B_{s1}&\cdots&A_{sr}+B_{sr} \end{pmatrix}$

数乘：

$\lambda A=\begin{pmatrix}\lambda A_{11}&\cdots&\lambda A_{1r}\\\vdots&&\vdots\\\lambda A_{s1}&\cdots&\lambda A_{sr}\end{pmatrix},\lambda\in\mathbb{R}$

乘法：

$A=\begin{pmatrix}A_{11}&\cdots&A_{1t}\\ \vdots&&\vdots\\A_{s1}&\cdots&A_{st}\end{pmatrix},\quad B=\begin{pmatrix}B_{11}&\cdots&B_{1r}\\\vdots&&\vdots\\ B_{t1}&\cdots&B_{tr}\end{pmatrix}=\begin{pmatrix}C_{11}&\cdots&C_{1r}\\ \vdots&&\vdots\\C_{s1}&\cdots&C_{sr}\end{pmatrix}$ $C_{ij}=\sum_{k=1}^{t}A_{ik}B_{kj} \quad(i=1,\cdots,s;j=1,\cdots,r)$

分块对角矩阵

设$A$是方阵，若$A$的分块矩阵在对角线上的子块$A_i(i=1,2,\cdots,s)$都是方阵，其余子块都是零矩阵，那么称$A$为分块对角矩阵

$A=\begin{pmatrix}A_1&\quad&\quad&O\\ \quad&A_2&\quad&\quad\\ \quad&\quad&\ddots&\quad\\ O&\quad&\quad&A_s\end{pmatrix}$

该分块对角矩阵$A$的秩等于对角线上子块的秩的和

$rank(A)=rank(A_1)+rank(A_2)+\cdots+rank(A_n)$

当$A_i(i=1,2,\cdots,s)$不是方阵时，上述定理依然有效