矩阵

定义

英国数学家阿瑟·凯莱中提出，对于线性方程组：

$\begin{cases} \ \ x+2y=3\\ 3x+4y=5 \end{cases}$

未知数的名字$x$,$y$根本就不重要，所以可把未知数的系数提出来，用一种称为矩阵(Matrix)的紧凑阵列来表示，该阵列称作系数矩阵

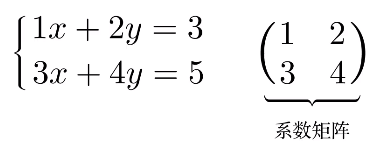
如果把等号右边的数字一起提出来，那么称为增广矩阵

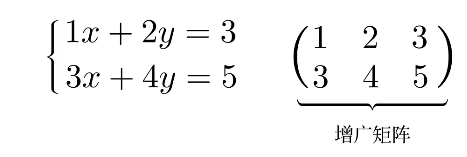
严格定义如下：

由$m×n$个数$a_{ij}(i=1,2,…m;j=1,2…n)$排成的$m$行$n$列的数表称为$m$行$n$列矩阵，简称$m×n$矩阵。为了表示这些数字是一个整体，总是加一个括弧

$A=\underbrace{\begin{pmatrix}a_{11}&a_{12}&...&a_{1n}\\a_{21}&a_{22}&...&a_{2n}\\...&...&&...\\a_{m1}&a_{m2}&...&a_{mn}\end{pmatrix}}_{\large n列}\left.\begin{aligned}\\\\\\\\\end{aligned}\right\}m行$

可以用$a_{ij}$表示该矩阵$A$的第$i$行$j$列的数字

矩阵$A_{m×n}$的第$i$行可以看做是行向量，同样的，第$j$列可以看做是列向量

如果行数列数相等，且都等于$n$，则称该矩阵为$n$阶方阵，简记为$A_n$

元素都是0的矩阵称为0矩阵，记作$O$

矩阵的诞生就是为了解线性方程组的

$\begin{cases} \ \ x+2y=3\\ 3x+4y=5 \end{cases} \implies \begin{cases} \ \ x+0y=?\\ 0x+\ \ y=? \end{cases}$

用矩阵表示就是

$\begin{pmatrix} 1&2&3\\ 3&4&5 \end{pmatrix} \implies \begin{pmatrix} 1&0&?\\ 0&1&? \end{pmatrix}$

增广矩阵的某行是可以乘除任意常数的，同时增广矩阵内某行也能加减任意行的倍数，所以可以将该矩阵化成

$\begin{cases} \ \ x+0y=-1\\ 0x+\ \ y=\ \ 2 \end{cases} \qquad \begin{pmatrix} 1&0&-1\\ 0&1&2 \end{pmatrix}$

从而解出方程

乘法的最初定义

将增广矩阵的第一行，第二行表示为：

$\begin{pmatrix} 1&2&3\\ 3&4&5 \end{pmatrix} \quad \begin{matrix} \boldsymbol{r_1}\\ \boldsymbol{r_2} \end{matrix}$

其中$r_1$,$r_2$都是行向量，那么刚才的简化过程中可以直接用矩阵表示：

$\begin{pmatrix} 1&2&3\\ 3&4&5 \end{pmatrix} \xrightarrow{\quad \boldsymbol{r_2}'=-3\boldsymbol{r_1}+\boldsymbol{r_2}\quad} \begin{pmatrix} 1&2&3\\ 0&-2&-4 \end{pmatrix}$

仔细观察这个过程，实际上包含了两个步骤

增广矩阵的第一行不变，即：$\boldsymbol{r_1}’=\boldsymbol{r_1}$
增广矩阵的第二行改变，即：$\boldsymbol{r_2}’=-3\boldsymbol{r_1}+\boldsymbol{r_2}$

首先，增广矩阵的第一行不变，凯莱说，下面这种乘法得到的结果就是$r_1$

其次，增广矩阵的第二行改变，凯莱又说，下面这种乘法得到的结果就是$\boldsymbol{r_2}’=-3\boldsymbol{r_1}+\boldsymbol{r_2}$

将{1,0}，{-3,1}组成一个矩阵，就能直接简化运算过程

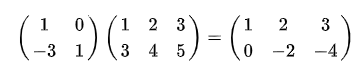
这就是矩阵乘法的最初定义

而之间的线性方程组的化简过程，可以完全用矩阵乘法来表示

$\begin{aligned} \begin{pmatrix}1&2&3\\3&4&5\end{pmatrix} &\xrightarrow[\quad r_2'=-3r_1+r_2\quad]{\quad r_1'=1r_1+0r_2\quad} \begin{pmatrix}1&0\\-3&1\end{pmatrix}\begin{pmatrix}1&2&3\\3&4&5\end{pmatrix}=\begin{pmatrix}1&2&3\\0&-2&-4\end{pmatrix}\\ \qquad\\ &\qquad\xrightarrow[\quad r_2'=0r_1-\frac{1}{2}r_2\quad] {\quad r_1'=1r_1+0r_2\quad} \begin{pmatrix}1&0\\0&-\frac{1}{2}\end{pmatrix} \begin{pmatrix}1&2&3\\0&-2&-4\end{pmatrix}= \begin{pmatrix}1&2&3\\0&1&2\end{pmatrix}\\ \qquad\\ &\qquad\xrightarrow[\quad r_2'=0r_1+1r_2\quad ]{\quad r_1'=r_1-2r_2\quad} \begin{pmatrix}1&-2\\0&1\end{pmatrix} \begin{pmatrix}1&2&3\\0&1&2\end{pmatrix}= \begin{pmatrix}1&0&-1\\0&1&2\end{pmatrix} \end{aligned}$

也可以将上述过程串在一起：

$\underbrace{\begin{pmatrix}1&-2\\0&1\end{pmatrix}\begin{pmatrix}1&0\\0&-\frac{1}{2}\end{pmatrix}\begin{pmatrix}1&0\\-3&1\end{pmatrix}}_{\large 注意顺序}\begin{pmatrix}1&2&3\\3&4&5\end{pmatrix}=\begin{pmatrix}1&0&-1\\0&1&2\end{pmatrix}$

最终只需要一个矩阵，就可以解出线性方程组

$\begin{pmatrix}1&-2\\0&1\end{pmatrix}\begin{pmatrix}1&0\\0&-\frac{1}{2}\end{pmatrix}\begin{pmatrix}1&0\\-3&1\end{pmatrix}=\begin{pmatrix}-2&1\\1.5&-\frac{1}{2}\end{pmatrix}$

高斯消元法

即通过方程组之间的消元和回代可以达到解方程组的目的

非零矩阵若满足：

非零行在零行（如果存在的话）的上面
非零行最左边的首非零元素在上一行（如果存在的话）的首非零元素的右面

满足上述要求的矩阵看上去像是阶梯状：

所以称为行阶梯形矩阵，非零行最左边的首非零元素称为主元

对角矩阵

若$n$阶方阵如下：

$\Lambda_{n}=\begin{pmatrix}\lambda_1&0&...&0\\0&\lambda_2&...&0\\...&...&&...\\ 0&0&...&\lambda_n\end{pmatrix}$

对角线以外元素都是0，这种方阵称为对角矩阵，也记作：

$\Lambda_{n}=diag(\lambda_1,\lambda_2,...,\lambda_n)$

对角矩阵的乘法非常简单：

$\begin{pmatrix}a_{1}&&&\\&a_{2}&&\\&&\ddots &\\&&&a_{n} \end{pmatrix}\begin{pmatrix}b_{1}&&&\\&b_{2}&&\\&&\ddots &\\&&&b_{n}\end{pmatrix}=\begin{pmatrix}a_{1}b_{1}&&&\\&a_{2}b_{2}&&\\&&\ddots &\\&&&a_{n}b_{n}\end{pmatrix}$

单位阵

如果$n$阶对角阵的对角线上元素为1：

$I_n=\begin{pmatrix}1&0&...&0\\0&1&...&0\\...&...&&...\\ 0&0&...&1\end{pmatrix}$

该对角阵称为$n$阶单位阵，或者简称为单位阵，用$E$表示

任何矩阵乘上单位阵之后结果不变

行最简形矩阵

若$A$是行阶梯形矩阵，并且还满足

主元为$1$
除主元外，其所在列其他元素均为0

初等行变换

在使用初等行变换之前，主要注意其目的

矩阵的初等变换不能同时行变换和列变换同时使用的。
在使用时候，还是要分场合进行讨论：

求矩阵的秩可以行初等变换和列初等变换混用，因为“经初等变换矩阵的秩不变”。（一定要用可逆变换，否则至少自己保证安全性。）
对于行列式求值而言，可以随便使用行变换和列变换，以及其它手段。行列式的计算只要得出结果出来就行了，是否使用哪种方法要结合行列式乘积定理来理解。
如果是解线性方程组只能用初等行变换，才能保证同解。
如果求矩阵的逆矩阵也只能用初等行变换。
解方程组$Ax=b$，那么两种变换都可以用，但不是无条件的。比如行变换就要同时作用于系数矩阵和右端项，列变换则需要保留信息，以便最后求解的时候用。

高斯消元法步骤虽然繁杂，实际上只需要三种操作就可以完成

完成高斯消元法只需要三种操作，这三种操作是作用在矩阵的行上的，所以又称为初等行变换。在单位阵上应用这三种初等行变换一次得到的矩阵称为初等行矩阵，也就是下列表格中最右的矩阵：

初等行矩阵乘上矩阵$A$，即$XA$，就相当于对矩阵进行了初等行变化

在已知矩阵$AB$，矩阵$B$的情况下，利用初等行变换让$B=AB$，对过程中使用到的初等行矩阵相乘，即为矩阵$A$（实际上此方法就是求逆矩阵的一种方法）

初等列变化

有初等行变换就有初等列变化

$\begin{array}{c|c|c} \hline \quad 初等列变换\quad &\quad 操作\quad &\quad 初等列矩阵\quad\\ \hline \\ \quad \color{SkyBlue}{倍加变换}\quad &\quad \boldsymbol{c_1}'=\boldsymbol{c_1}+k\boldsymbol{c_2}\quad &\quad \begin{pmatrix}1&0&0\\{\color{red}{k}}&1&0\\0&0&1\end{pmatrix}\quad \\ \\ \hline \\ \quad \color{Goldenrod}{倍乘变换}\quad &\quad \boldsymbol{c_1}'=k\boldsymbol{c_1} (k\neq 0)\quad & \quad \begin{pmatrix}{\color{red}{k}}&0&0\\0&1&0\\0&0&1\end{pmatrix}\quad \\ \\ \hline \\ \quad \color{orange}{对换变换}\quad &\quad \boldsymbol{c_1}\leftrightarrow \boldsymbol{c_2}\quad & \quad \begin{pmatrix}{\color{red}{0}}&{\color{red}{1}}&0\\ {\color{red}{1}}&{\color{red}{0}}&0\\{\color{red}{0}}&{\color{red}{0}}&1\end{pmatrix}\quad \\ \\ \hline \end{array}$

矩阵$A$乘上初等列矩阵，即$AX$，就相当于对矩阵进行了初等行变化

运算

加法

两个矩阵的行数相等、列数也相等时，就称它们是同型矩阵

若$A=(a_{ij})$与$B=(b_{ij})$是同型矩阵，并且他们对应元素都相等，则矩阵$A$和矩阵$B$相等

$A=B$

只有同型矩阵之间才能相加

$A+B=\begin{pmatrix}a_{11}+b_{11}&a_{12}+b_{12}&...&a_{1n}+b_{1n}\\a_{21}+b_{21}&a_{22}+b_{22}&...&a_{2n}+b_{2n}\\ ...&...&&...\\a_{m1}+b_{m1}&a_{m2}+b_{m2}&...&a_{mn}+b_{mn}\end{pmatrix}$

乘法

数$k$与矩阵$A$的乘积记作：

$kA$

规定为：

$kA=Ak= \begin{pmatrix} ka_{11}&ka_{12}&\cdots&ka_{1n}\\ ka_{21}&ka_{22}&\cdots&ka_{2n}\\ \cdots&\cdots& &\cdots\\ ka_{m1}&ka_{m2}&\cdots&ka_{mn}\end{pmatrix}$

矩阵之间的相乘，是需要满足一定合法性的：

$m×n$的矩阵只能和$n×p$矩阵相乘
相乘后矩阵大小为$m×p$

结合乘法的最初定义其实很好理解，$A$矩阵的每一列都要对应到$B$矩阵的每一行

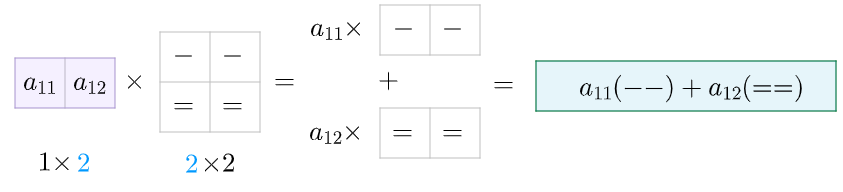
行观点

在运算时，将按照行的顺序进行运算

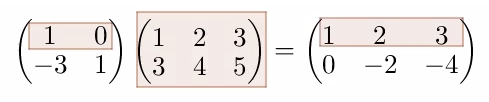
假设有行向量$x$和矩阵$A$，如果计算$xA$，很适合用行观点来看待矩阵乘法，把结果看作$A$矩阵行向量的线性组合

$\boldsymbol{x}\boldsymbol{A}=\begin{pmatrix}\color{blue}{x_1}&\color{blue}{x_2}&\cdots&\color{blue}{x_m}\end{pmatrix} \begin{pmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\quad&\quad&\vdots\\ a_{m1}&a_{m2}&\cdots&a_{mn} \end{pmatrix}=$ $\color{blue}{x_1}\begin{pmatrix}a_{11}&a_{12}&\cdots&a_{1n}\end{pmatrix}+ \color{blue}{x_2}\begin{pmatrix}a_{21}&a_{22}&\cdots&a_{2n}\end{pmatrix}+\cdots+ \color{blue}{x_m}\begin{pmatrix}a_{m1}&a_{m2}&\cdots&a_{mn}\end{pmatrix}$

此时，$A$在行向量$x$的右边，所以可说$A$右乘$x$

列观点

同行观点类似，如果右边是多列矩阵，可以看作多次运用矩阵列观点，并将结果放置在合适的位置：

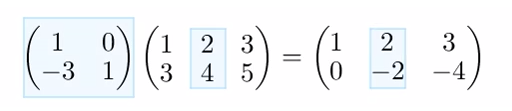
假设有行向量$x$和矩阵$A$，如果计算$Ax$，很适合用列观点来看待矩阵乘法，把结果看作$A$矩阵列向量的线性组合

$\boldsymbol{A}\boldsymbol{x}=\begin{pmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\quad&\quad&\vdots\\ a_{m1}&a_{m2}&\cdots&a_{mn} \end{pmatrix} \begin{pmatrix}\color{blue}{x_1}\\\color{blue}{x_2}\\\vdots\\\color{blue}{x_n}\end{pmatrix}=\color{blue}{x_1}\begin{pmatrix}a_{11}\\a_{21}\\\vdots\\a_{m1}\end{pmatrix} +\color{blue}{x_2}\begin{pmatrix}a_{12}\\a_{22}\\\vdots\\a_{m2}\end{pmatrix} +\cdots+ \color{blue}{x_n}\begin{pmatrix}a_{1n}\\a_{2n}\\\vdots\\a_{mn}\end{pmatrix}$

此时，$A$在列向量$x$的左边，所以可说$A$左乘$x$

点积观点

设$A=(a_{ij})$是一个$m×s$矩阵，$B=(b_{ij})$是一个$s×n$矩阵，那么规定$A$与$B$的乘积是一个$

$c_{ij}=\boldsymbol{a}_{i*}\cdot\boldsymbol{b}_{*j}=a_{i1}b_{1j}+a_{i2}b_{2j}+...+a_{is}b_{sj}=\displaystyle \sum_{k=1}^s a_{ik}b_{kj}\\(i=1,\cdots,m;j=1,\cdots,n)$

并把乘积记作

$C=AB$

上述定义的意思是，用左侧矩阵的行向量点积上右侧矩阵的列向量可以得到矩阵中的每个元素：

非常适合口算矩阵乘法

矩阵乘法在有些情况下满足交换律，比如：

$A,B$互逆，即$B=A^{-1}$的情况下，$AB=AA^{-1}=E=A^{-1}A=BA$
或者是$AB$中有个矩阵为零矩阵
或者两个矩阵都是对角线矩阵
或者$B$是$A$的伴随矩阵，因为有性质：$AA^{*}=|A|E$

幂

设$A$是方阵，定义：

$A^1=A,\quad A^2=A^1A^1,\quad\cdots,\quad A^{k+1}=A^kA^1$

其中$k$为正整数

对角阵的幂运算：

$\Lambda^n=\left(\begin{array}{ccccc}{\lambda_{1}^n} \\ {} & {\lambda_{2}^n} \\ {} & {} & {} \\ {} & {} & {} & {\ddots} \\ {} & {} & {} & {} & {\lambda_{m}^n}\end{array}\right)$

求矩阵的幂有如下思路：

若矩阵可以相似对角化后，那么先相似对角化再求$A^n$ ,此属于常规思路
若$A$是由一个行向量与一个列向量相乘所得 (此时矩阵特点为每一个行（列）向量都是其余行（列）向量的倍数，即秩为1的方阵)，则可按如下处理：
$l=\beta^{T}\alpha=\alpha^{T}\beta=∑a_{ii}$ $A^m=l^{m-1}A$
之所以这样算，是因为可以这样拆分：
$A^2=(\alpha\beta^{T})(\alpha\beta^{T})=\alpha(\beta^{T}\alpha)\beta^{T}=lA$
关于这种特殊方阵，其计算有许多巧妙之处，可以通过其平方化进行有效化简的作用
利用分块矩阵来求幂

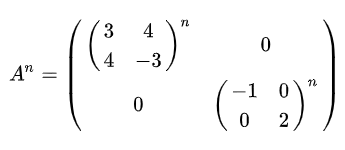
矩阵的高次幂和矩阵的基础解系是一样的，即$A^nx=0$和$Ax=0$同解

转置

把矩阵$A$的行换成同序数的列，该操作称为矩阵的转置运算，转置运算后可以得到一个新矩阵，该矩阵称为A的转置矩阵，记作$A^T$

$A=(a_{ij}),\quad A^\mathrm{T}=(a_{ji})$

容易得到转置运算有以下性质：

$(A^\mathrm{T})^\mathrm{T}=A$
$(AB)^\mathrm{T}=B^\mathrm{T}A^\mathrm{T}$
$(A^\mathrm{T})^n=(A^n)^\mathrm{T}$
$(A+B)^\mathrm{T}=A^\mathrm{T}+B^\mathrm{T}$

将$A^T=A$的矩阵称作对称矩阵，将$A^T=-A$的矩阵称为反对称矩阵

乘法的几何意义

矩阵的左乘$Aa=b$的几何意义是，在矩阵$A$的帮助下，将$a$变换成了$b$

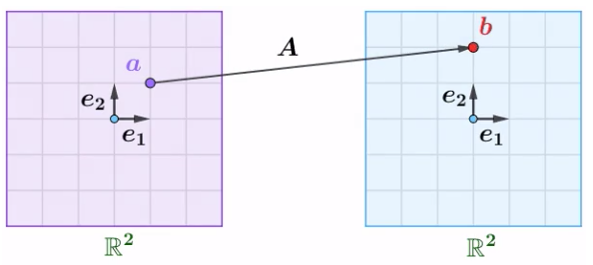
根据转置运算的规则，可以得到矩阵的右乘：

$\boldsymbol{A}\boldsymbol{a}=\boldsymbol{b}\implies (\boldsymbol{A}\boldsymbol{a})^\mathrm{T}=\boldsymbol{b}^\mathrm{T}\implies\boldsymbol{a}^\mathrm{T}\boldsymbol{A}^\mathrm{T}=\boldsymbol{b}^\mathrm{T}$

矩阵的右乘$a^TA^T=b^T$的几何意义是，在矩阵$A^T$的帮助下，将$a^T$变换成了$b^T$

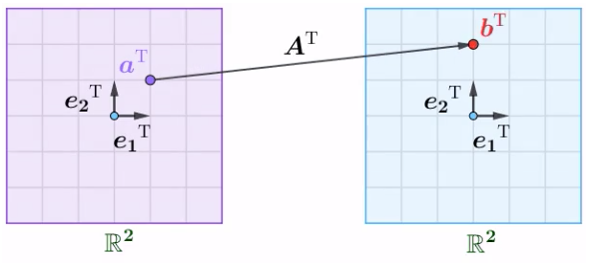
左乘、右乘的几何意义是完全一样的，只是代数形式不同：

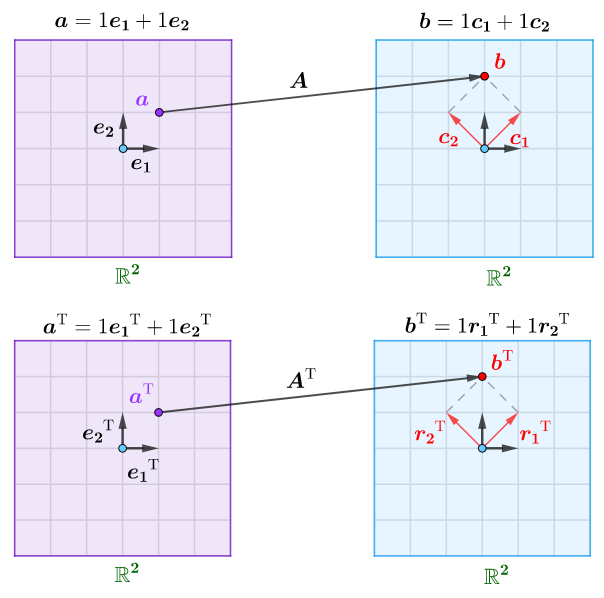
所以，我们可以认为转置运算在这里只会导致代数形式上的变化，没有具体的几何意义。