行列式

由来

历史上，定义行列式的目的就是为了解线性方程组。对于一元二次方程组

$\begin{cases}a_{11}x_1+a_{12}x_2=b_1\\a_{21}x_1+a_{22}x_2=b_2\end{cases}$

如果有唯一解，那么可以通过高斯消元法得到

$\begin{cases} x_1=\displaystyle \frac{b_1a_{22}-a_{12}b_2}{a_{11}a_{22}-a_{12}a_{21}}\\ \quad \\ x_2=\displaystyle \frac{b_2a_{11}-a_{21}b_1}{a_{11}a_{22}-a_{12}a_{21}} \end{cases}$

同样的，该结论可以推广到$n$元一次线性方程组，简化$n$元一次线性方程组的解，找出其中的规律，这个过程中产生了行列式

低阶行列式

二阶行列式

二阶行列式是这么定义的，交叉相乘，之后相减：

$\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}$

再看刚才二元一次方程组的解：

$\begin{cases} x_1=\displaystyle \frac{b_1a_{22}-a_{12}b_2}{a_{11}a_{22}-a_{12}a_{21}}\\ \quad \\ x_2=\displaystyle \frac{b_2a_{11}-a_{21}b_1}{a_{11}a_{22}-a_{12}a_{21}} \end{cases}$

解的分母都是：

$a_{11}a_{22}-a_{12}a_{21}$

带入行列式的规则，可以表示为

$\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}$

而分子也可以表示为

$b_1a_{22}-a_{12}b_2=\begin{vmatrix}b_1&a_{12}\\b_2&a_{22}\end{vmatrix}$ $b_2a_{11}-a_{21}b_1=\begin{vmatrix}a_{11}&b_1\\a_{21}&b_2\end{vmatrix}$

而线性方程组的解可以用行列式来表示

$\begin{cases} x_1=\displaystyle \frac{b_1a_{22}-a_{12}b_2}{a_{11}a_{22}-a_{12}a_{21}}\\ \quad \\ x_2=\displaystyle \frac{b_2a_{11}-a_{21}b_1}{a_{11}a_{22}-a_{12}a_{21}} \end{cases}\Longleftrightarrow \begin{cases} x_1=\displaystyle \frac{\begin{vmatrix}b_1&a_{12}\\b_2&a_{22}\end{vmatrix}}{\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}}\\ \quad\\ x_2=\displaystyle \frac{\begin{vmatrix}a_{11}&b_1\\a_{21}&b_2\end{vmatrix}}{\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}} \end{cases}$

三阶行列式

三阶行列式的定义比较复杂，可以用对角线法则定义

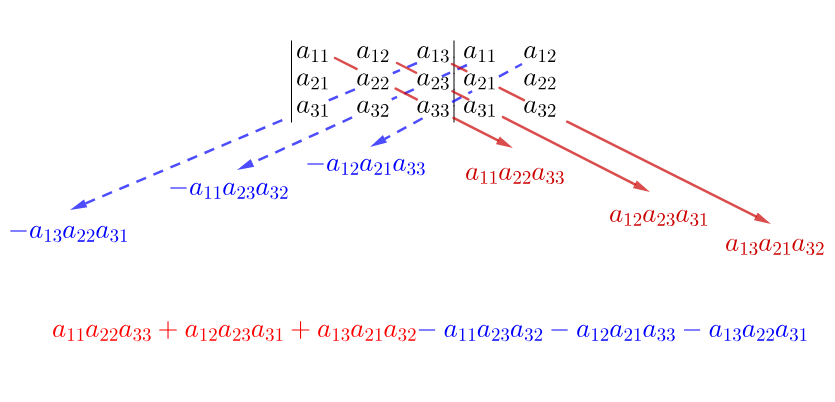
$\underbrace{\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}_{三阶行列式} =\underbrace{a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31}}_{运算规则}$

三元方程组的解同样也可以通过行列式来表示

$x_1=\frac{\begin{vmatrix}b_1&a_{12}&a_{13}\\ b_2&a_{22}&a_{23}\\b_3&a_{32}&a_{33}\end{vmatrix}} {\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}\quad x_2=\frac{\begin{vmatrix}a_{11}&b_1&a_{13}\\ a_{21}&b_2&a_{32}\\a_{31}&b_3&a_{33}\end{vmatrix}} {\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}\quad x_3=\frac{\begin{vmatrix}a_{11}&a_{12}&b_1\\ a_{21}&a_{22}&b_2\\a_{31}&a_{32}&b_3\end{vmatrix}} {\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}$

定义

全排列

把$n$个不同的元素排成一列，叫做这$n$元素的全排列（简称排列)。

数列$1,2,3$的全排列就有以下6种

$1,2,3\quad 1,3,2\quad 2,1,3 \quad 2,3,1\quad 3,1,2\quad 3,2,1$

逆序数

规定数列从小到大为正序，否则为逆序，在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。

比如数列$3,2,5,4,1$的逆序数为1+1+4=6

奇排列和偶排列

逆序数为奇数的排列称为奇排列，逆序数为偶数的排列称为偶排列。

一个排列中任意的两个元素对换，排列改变奇偶性。

以三阶行列式为例：

$\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix} =a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31}$

观察每一项的下标，下标第一项都是以$1,2,3$排列，而第二项是$1,2,3$的全排列

$\begin{aligned} a_{1{\color{red}1}}a_{2{\color{red}2}}a_{3{\color{red}3}}&&1,2,3\implies t=0&&(-1)^t=+1\\ -a_{1{\color{red}1}}a_{2{\color{red}3}}a_{3{\color{red}2}}&&1,3,2\implies t=1&&(-1)^t=-1\\ -a_{1{\color{red}2}}a_{2{\color{red}1}}a_{3{\color{red}3}}&&2,1,3\implies t=1&&(-1)^t=-1\\ a_{1{\color{red}2}}a_{2{\color{red}3}}a_{3{\color{red}1}}&&2,3,1\implies t=2&&(-1)^t=+1\\ a_{1{\color{red}3}}a_{2{\color{red}1}}a_{3{\color{red}2}}&&3,1,2\implies t=2&&(-1)^t=+1\\ -a_{1{\color{red}3}}a_{2{\color{red}2}}a_{3{\color{red}1}}&&3,2,1\implies t=3&&(-1)^t=-1 \end{aligned}$

如果是奇排列，那么带负号，如果是偶排列，则不带

三阶行列式有如下表示

$\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=\sum (-1)^t a_{1p_1}a_{2p_2}a_{3p_3}$

其中 $t$ 表示排列 $p_1,p_2,p_3$ 的逆序数，$\sum$表示对所有排列求和

将结论推广到所有的行列式中，$n$阶行列式的定义为：

$D=\begin{vmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\quad&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn} \end{vmatrix}$

其值为

$D=\sum(-1)^ta_{1p_1}a_{2p_2}\cdots a_{np_n}$

全排列的意义在于可以求解$n$($n>3$)阶行列式，特定项的系数，比如$4$阶行列式里$x^4$项的系数

克拉默法则

观察三元方程组的解

可以看到如下规律：

分母都是系数组成的行列式
分子也是系数组成的行列式，只是对应于不同的$x_i$，第$i$列被替换为了常数项

上面的规律推广到$n$元线性方程组的话，就是克拉默法则：

如果有$n$个未知数，$n$个方程组组成的线性方程式，他的系数矩阵$A$的行列式不等于0，即

$|A|=\begin{vmatrix}a_{11}&\cdots&a_{1n}\\\vdots&&\vdots\\ a_{n1}&\cdots&a_{nn}\end{vmatrix}\neq 0$

则方程组有唯一解：

$\displaystyle x_1=\frac{|A_1|}{|A|}\quad x_2=\frac{|A_2|}{|A|}\quad...\quad x_n=\frac{|A_n|}{|A|}$

其中$A_j$是把系数矩阵$A$中的第$j$元素用方程组右端的常数项代替后所得到的$n$阶矩阵

$A_j=\begin{pmatrix} a_{11}&\cdots&a_{1,j-1}&{\color{red}{b_1}}&a_{1,j+1}&\cdots&a_{1n}\\ \vdots&&\vdots&{\color{red}{\vdots}}&\vdots&&\vdots\\ a_{n1}&\cdots&a_{n,j-1}&{\color{red}{b_n}}&a_{n,j+1}&\cdots&a_{nn} \end{pmatrix}$

几何意义

行列式除了是一种运算法则外，更重要的意义是：对于某方阵$A$，它的行列式$|A|$,是列向量矩阵函数$Ax=y$的伸缩比例

伸缩比例的意思是变换后和变换前的有向面积之比，假设有二阶方阵$A_2$，和行列式$|A_2|$

$\boldsymbol{A}_2= \begin{pmatrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{pmatrix},\quad |\boldsymbol{A}_2|= \begin{vmatrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{vmatrix}$

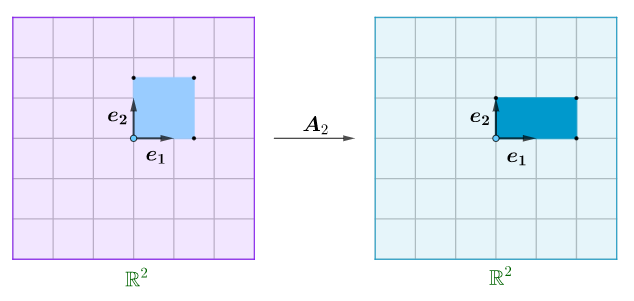
映射前和映射后面积之比，就是伸缩比例

行列式的值有三种情况：

$|A_2|>0$
$|A_2|=0$
$|A_2|<0$

当$|A_2|>0$时，会导致映射图形正向伸缩

当$|A_2|=0$，会导致维度降低，实际上只有$A$不满秩，$|A|=0$

显然，如果行列式为0，则$A$不满秩=$A$不可逆=$A$中的向量线性相关

当$|A_2|<0$时，会导致映射图形反向伸缩

对于二阶行列式，其在变换前的基是自然基$e_1,e_2$，而变换后，$e_1,e_2$被映射成了$c_1,c_2$，即：

$\boldsymbol{A}_2\boldsymbol{e_1}=\boldsymbol{c_1},\quad \boldsymbol{A}_2\boldsymbol{e_2}=\boldsymbol{c_2}$

也就是说$e_1,e_2$围成的正方形被映射成了$c_1,c_2$围成的平行四边形：

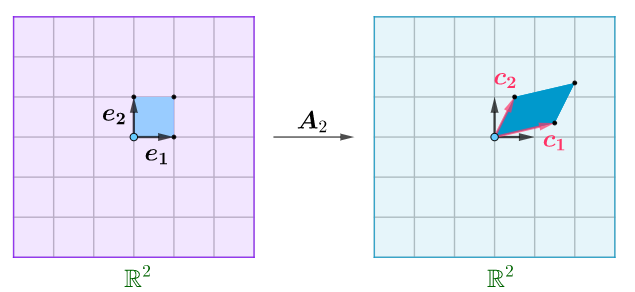
可以算出$c_1,c_2$围成的平行四边形的有向面积就是二阶行列式：

$\boldsymbol{c_1}、\boldsymbol{c_2}围成的平行四边形的有向面积\ =\ |\boldsymbol{A}_2|$

而到了三阶行列式，面积之比会变为有向体积之比

子式和余子式

子式

在$m×n$矩阵$A$中，任取$k$行与$k$列，位于这些行，列交叉处的$k^2$个元素，不改变它们在$A$中所处的位置次序而得的$k$阶行列式，称为矩阵$A$的$k$阶子式

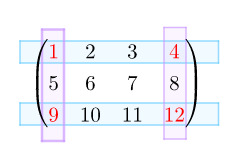
取一，三行和一，四列构成的行列式就是矩阵的一个子式

主子式

如果选取的行号和列号相同，取出来的子式就是主子式，如果取$n$阶矩阵的前$n$行$n$列，取出来的子式就是顺序主子式

而教科书中，是如此定义矩阵的秩的：

设在矩阵$A$中有一个不等于0的$r$阶子式$|B_r|$，且所有$r+1$阶子式全等于0，那么$|B_r|$称为矩阵$A$的最高阶非零子式，数$r$称为矩阵$A$的秩

如果一个行列式对应的矩阵（方阵）不是满秩矩阵，则这个行列式的值为0

余子式

在$n$阶行列式中，把$a_{ij}$所在的第$i$行和第$j$列划去后，留下来的$n-1$阶行列式叫做$a_{ij}$的余子式，记作$M_{ij}$

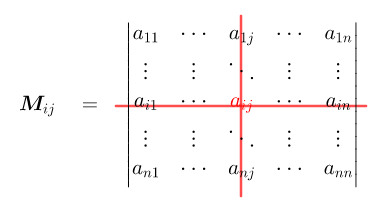
实际上在之前提到三阶行列式的计算方法中，就有余子式

$\begin{aligned} \begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix} &=a_{11}\overbrace{\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}}^{a_{11}\text{的余子式}}-a_{21}\overbrace{\begin{vmatrix}a_{12}&a_{13}\\a_{32}&a_{33}\end{vmatrix}}^{a_{21}\text{的余子式}}+a_{31}\overbrace{\begin{vmatrix}a_{12}&a_{13}\\a_{22}&a_{23}\end{vmatrix}}^{a_{31}\text{的余子式}}\\ \\ &=a_{11}\boldsymbol{M}_{11}-a_{21}\boldsymbol{M}_{21}+a_{31}\boldsymbol{M}_{31} \end{aligned}$

在余子式的基础上，还可以定义$A_{ij}$，称为$a_{ij}$的代数余子式

$A_{ij}=(-1)^{i+j}M_{ij}$

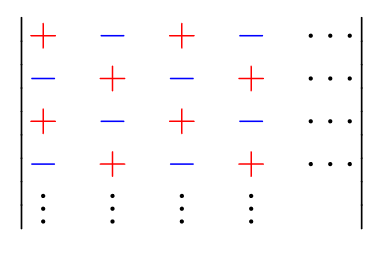
总结：

性质

转置后行列式的值不变

记
$D= \begin{vmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\quad&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn} \end{vmatrix}, D^\mathrm{T}= \begin{vmatrix} a_{11}&a_{21}&\cdots&a_{n1}\\ a_{12}&a_{22}&\cdots&a_{n2}\\ \vdots&\vdots&\quad&\vdots\\ a_{1n}&a_{2n}&\cdots&a_{nn} \end{vmatrix}$
其中行列式$D^T$称为行列式$D$的转置行列式

有如下结论
$|D|=|D^T|$
因为行列式$|A|$和$|A^T|$代表的是同一个映射，所以不变
某行（列）有公因数$k$，可以直接把$k$提出来
$D=\begin{vmatrix} ka_{11}&ka_{12}&\cdots&ka_{1n} \end{vmatrix}=k\begin{vmatrix} a_{11}&a_{12}&\cdots&a_{1n} \end{vmatrix}$
两行（列）互换，行列式的值变号
$D=\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\end{vmatrix}=-\begin{vmatrix}a_{21}&a_{22}&\cdots&a_{2n}\\a_{11}&a_{12}&\cdots&a_{1n}\end{vmatrix}$
可以从逆序数的角度理解，如果两行互换了，那么其每一项的逆序数都会反号，即减数变成被减数，被减数变成减数，则最后行列式的值会变号

根据此性质，可以得出，如果行列式中有两行（列）相同，那么行列式的值为0，即交换(相等的)两行，|A| = -|A|，则|A| = 0
对于$n$阶方阵$\boldsymbol{A}$，反复运用“行列式的数乘”可得：
$|k\boldsymbol{A}|=\begin{vmatrix} {\color {blue}k}a_{11}&{\color {blue}k}a_{12}&\dots&{\color {blue}k}a_{1n}\\ \vdots &\vdots &\ddots &\vdots\\ {\color {blue}k}a_{i1}&{\color{blue}k}a_{i2}&\dots&{\color{blue}k}a_{in}\\ \vdots &\vdots &\ddots &\vdots \\ {\color {blue}k}a_{n1}&{\color {blue}k}a_{n2}&\dots &{\color {blue}k}a_{nn} \end{vmatrix}=k^n|\boldsymbol{A}|$
如果行列式某行（列）每一项都是两个数的和，则可以把行列式拆成两个行列式之和
$\begin{vmatrix}a_{1}+b_{1}&a_{2}+b_{2}&a_{3}+b_{3}\\c_1&c_{2}&c_{3}\\d_{1}&d_{2}&d_{3}\end{vmatrix}=\begin{vmatrix}a_{1}&a_{2}&a_{3}\\c_1&c_{2}&c_{3}\\d_{1}&d_{2}&d_{3}\end{vmatrix}+\begin{vmatrix}b_{1}&b_{2}&b_{3}\\c_1&c_{2}&c_{3}\\d_{1}&d_{2}&d_{3}\end{vmatrix}$
从展开式理解，每一项都会有$a_i+b_i$，所以可以拆开再合并同类项
把某行（列）的$k$倍加到另外一行，行列式的值不变
$D=\begin{vmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}=\begin{vmatrix}a_{1}&a_{2}&a_{3}\\b_{1}+ka_1&b_{2}+ka_2&b_{3}+ka_3\end{vmatrix}$
可以通过性质2,3,4来证明
$\begin{vmatrix}a_{1}&a_{2}&a_{3}\\b_{1}+ka_1&b_{2}+ka_2&b_{3}+ka_3\end{vmatrix}=\begin{vmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}+k\begin{vmatrix}a_{1}&a_{2}&a_{3}\\a_1&a_2&a_3\end{vmatrix}$
而
$k\begin{vmatrix}a_{1}&a_{2}&a_{3}\\a_1&a_2&a_3\end{vmatrix}=0$
所以性质成立
对于同阶方阵$A$,$B$，有：
$|\boldsymbol{A}\boldsymbol{B}|=|\boldsymbol{A}||\boldsymbol{B}|$

三角行列式

$|\boldsymbol{A}|= \begin{vmatrix} a_{11}&&&\\ a_{21}&a_{22}&&0\\ \vdots &\vdots &\ddots &\\ a_{n1}&a_{n2}&\dots &a_{nn} \end{vmatrix} = a_{11}a_{22}\cdots a_{nn}$

而对于反三角行列式：

$|\boldsymbol{A}|=\begin{vmatrix}&&&\lambda_1\\&&\lambda_2&\\&\mathstrut^{.^{.^{.}}}&&\\ \lambda_n&&&\end{vmatrix}$

将行列式$|A|$的第$n$列和$n-1$列对换，再将$n-1$列和$n-2$列对换，以此类推，经过$n-1$次列变换，可以将第$n$列换到了第一列，得到如下行列式：

$|\boldsymbol{A}_1|=\begin{vmatrix}\lambda_1&\cdots&0&0&\\ 0&\cdots&0&\lambda_2&\\ 0&\cdots&\lambda_3&0&\\ \vdots&&\vdots&\vdots&\\ 0&\lambda_n&0&\cdots&\end{vmatrix}$

根据上文提到的行列式对换性质，每换一次，正负号都会发生改变，这里对换了$n-1$次，所以：

$|\boldsymbol{A}_1|=(-1)^{n-1}|\boldsymbol{A}|$

按上面的方法，将$|A_1|$j进行$n-2$次对换，将第$n$列换到第二列，以此类推，最终可以将反三角行列式换成三角行列式

一共发生了：$(n-1)+(n-2)+\cdots+1=\frac{1}{2}n(n-1)$对换

所以：

$|\boldsymbol{A}|=(-1)^{\frac{1}{2}n(n-1)}|\boldsymbol{A}_{n-1}|=(-1)^{\frac{1}{2}n(n-1)}\lambda_1\lambda_2\cdots\lambda_n$

应用到分块矩阵上：

$\boldsymbol{A}=\begin{pmatrix}\boldsymbol{B}&\boldsymbol{O}\\\boldsymbol{C}&\boldsymbol{D}\end{pmatrix}$

则有：

$|\boldsymbol{A}|=|\boldsymbol{B}||\boldsymbol{D}|$ $\boldsymbol{A}=\begin{pmatrix}\boldsymbol{B}&\boldsymbol{C}\\\boldsymbol{D}&\boldsymbol{O}\end{pmatrix}$

则有：

$|\boldsymbol{A}|=(-1)^{mn}|\boldsymbol{C}||\boldsymbol{D}|$

可以将此分块矩阵换成之前的形式，总共要经历$m×n$次交换

拉普拉斯展开

$n$阶方阵$A=(a{ij})$的行列式可以表示为该方阵$A$的某一行的各元素和其对应的代数余子式乘积之和

$|\boldsymbol{A}|=a_{i1}A_{i1}+a_{i2}A_{i2}+...+a_{in}A_{in}\quad (i=1,2,...,n)$

或者说是某一列和其代数余子式的乘积之和：

$|\boldsymbol{A}|=a_{1j}A_{1j}+a_{2j}A_{2j}+...+a_{nj}A_{nj}\quad (j=1,2,...,n)$

这种计算行列式的方法是拉普拉斯展开

根据拉普拉斯展开，可以得到以下推论：

$a_{j1}A_{i1}+a_{j2}A_{i2}+...+a_{jn}A_{in}=0\quad (i\neq j)$

就是说如果在某行的代数余子式前的系数刚好是另一行或列的系数，那么最后的结果为0

范德蒙行列式

$|\boldsymbol{A}|=\begin{vmatrix} 1&1&1&\cdots&1\\ x_1&x_2&x_3&\cdots&x_n\\ x_1^2&x_2^2&x_3^2&\cdots&x_n^2\\ \vdots &\vdots&\vdots&\ddots&\vdots\\ x_1^{n-1}&x_2^{n-1}&x_3^{n-1}&\cdots&x_n^{n-1} \end{vmatrix} = \displaystyle \prod_{1\leq j < i \leq n}(x_i-x_j)$

其中$\displaystyle \prod_{1\leq j < i \leq n}(x_i-x_j)$代表连乘

范德蒙行列式主要是为了解决插值问题，即通过离散的数据求未知数据

通过假设曲线的方程组，类似于$y=a_0+a_1x+a_2x^2+a_3x^3$的形式，然后通过列出方程组的系数矩阵，矩阵的形式就是范德蒙行列式，最后利用克拉默法则求解

伴随矩阵

除了初等行变换以及高斯若尔当法之后，还可以通过行列式来求矩阵：

由$|A|$的代数余子式$A_{ij}$所构成的矩阵，称为$A$的代数余子式矩阵：

$\boldsymbol{C}= \begin{pmatrix} A_{11}&A_{12}&\cdots&A_{1n}\\ A_{21}&A_{22}&\cdots&A_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ A_{n1}&A_{n2}&\cdots&A_{nn} \end{pmatrix}$

其转置称为$A$的伴随矩阵，记作$A^*$

$\boldsymbol{A}^{*}=\boldsymbol{C}^\mathrm{T}= \begin{pmatrix} A_{11}&A_{21}&\cdots&A_{n1}\\ A_{12}&A_{22}&\cdots&A_{n2}\\ \vdots&\vdots&\ddots&\vdots\\ A_{1n}&A_{2n}&\cdots&A_{nn} \end{pmatrix}$

根据可逆和行列式的关系，若$|A|≠0$，则矩阵可逆，可证明：

$\boldsymbol{A}^{-1}=\frac{1}{|\boldsymbol{A}|}\boldsymbol{A}^{*}$

证明过程

证明过程如下：

设$A=(a_{ij})$，记$AA^*=(b_{ij})$，

其中$A$的行向量可表示为：$(a_{i1},a_{i2},\cdots,a_{in})$，$A^*$的$j$列为列向量$\begin{pmatrix}A_{j1}\\A_{j2}\\\vdots\\A_{jn}\end{pmatrix}$所以：

$b_{ij}=a_{i1}A_{j1}+a_{i2}A_{j2}+...+a_{in}A_{jn}$

根据拉普拉斯展开，代数余子式乘其他行的值为0

$b_{ij}=a_{i1}A_{j1}+a_{i2}A_{j2}+...+a_{in}A_{jn}= \begin{cases}|\boldsymbol{A}|,\quad i=j\\ 0, \quad i\neq j\end{cases}$

所以最后的结果是

$\boldsymbol{A}\boldsymbol{A}^{*}=\begin{pmatrix}|\boldsymbol{A}|&0&\cdots&0\\ 0&|\boldsymbol{A}|&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&|\boldsymbol{A}| \end{pmatrix}=|\boldsymbol{A}|\boldsymbol{I}$

故：

$\frac{1}{|\boldsymbol{A}|}\boldsymbol{A}^{*}\boldsymbol{A}=\boldsymbol{I}$

所以

$\boldsymbol{A}^{-1}=\frac{1}{|\boldsymbol{A}|}\boldsymbol{A}^{*}$

性质

伴随矩阵行列式和原矩阵行列式关系：

$AA^*=|A|E$

如果$A$可逆，那么$A^*=|A|A^{-1}$，则：

$|A^*|=||A|A^{-1}|=|A|^{n}|A^{-1}|=|A|^{n-1}$

多个矩阵的伴随矩阵：

$(AB)^{*}=B^*A^*$

如果$A_{ij}=a_{ij}$，那么$A^*=A^T$

设$\boldsymbol{A}$为$n$阶方阵，则：

$rank(\boldsymbol{A})=n\iff rank(\boldsymbol{A}^*)=n$
$rank(\boldsymbol{A})=n-1\iff rank(\boldsymbol{A}^*)=1
$
$rank(\boldsymbol{A}) < n-1\iff rank(\boldsymbol{A}^*) = 0$

根据秩的定义：设在矩阵$A$中有一个不等于0的$r$阶子式$|B_r|$，且所有$r+1$阶子式全等于0，那么$|B_r|$称为矩阵$A$的最高阶非零子式，数$r$称为矩阵$A$的秩

如果矩阵$A$满秩，那么$n$阶子式也满秩，所以$rank(\boldsymbol{A})=n\iff rank(\boldsymbol{A}^*)=n$

如果矩阵$rank(\boldsymbol{A})=n-1$，说明必有$n-1$阶子式非0，那么其代数余子式也非0，根据$A^*$的定义，其必不为0，又根据秩零定理，其秩必为1

如果$rank(A)<n-1$，说明$n-1$阶子式全部为0，那么$A^*$就肯定是零矩阵$O$了