线性方程组的解

讨论线性方程组的解，主要讨论以下三点：

解的存在性：在$Ax=b$中，是否有$x$与$b$对应
解的个数：在$Ax=b$中，有多少个$x$与$b$对应
解集：在$Ax=b$中，具体是$x$与$b$相对应

实际上，在矩阵函数的映射中，已经得出了结论了

单射（列）	满射（行）	结果
√	√	必有解，且为唯一解
√	×	有可能有解，有可能无解，若有解，必为唯一解
×	√	必然有解，解必然不唯一
×	×	只有非零解

针对齐次方程$Ax=O$，还有如下结论

单射（列）	满射（行）	结果
√	√	必有解，且为唯一解
√	×	只有零解
×	√	必然有解，解必然不唯一
×	×	只有非零解

但是只是部分条件，因为很多结论只是充分条件罢了

比如说行满秩(满射)可以推出必然有解，但是必然有解的情况，并不能推出行满秩

所以还需要进一步讨论线程方程组的解

对于线性方程组$Ax=b$，它的增广矩阵为$B=(A|b)$，如果$A$为$m×n$的矩阵那么：

有唯一解，当且仅当$rank(A)=rank(B)=n$
有无数解，当且仅当$rank(A)=rank(B)<n$
无解，当且仅当$rank(A)<rank(B)$

简洁的结论，如果增广矩阵的秩比系数矩阵的大，只能说明结果向量和系数矩阵线性不相关，当然无解

方程组的解集(基础解系)

对于线性方程组$Ax=b$而言：

$b=0$时，即$Ax=0$时，称为齐次线性方程组
$b≠0$时，称为非齐次线性方程组

求解集的步骤一般是：

先写出线性方程组的增广矩阵
$\boldsymbol{B}=(\boldsymbol{A}\ |\ \boldsymbol{0})= \left( {\begin{array}{c|c} \begin{matrix} 1 & 1 \\ 1 & 1 \\ \end{matrix}& \begin{matrix} 0 \\ 0 \\ \end{matrix} \end{array}} \right)$
变换为行最简形矩阵(关键)
$\left( {\begin{array}{c|c} \begin{matrix} 1 & 1 \\ 1 & 1 \\ \end{matrix}& \begin{matrix} 0 \\ 0 \\ \end{matrix} \end{array}} \right) \xrightarrow{\quad \boldsymbol{r}_2'=\boldsymbol{r}_2-\boldsymbol{r}_1\quad} \left( {\begin{array}{c|c} \begin{matrix} 1 & 1 \\ 0 & 0 \\ \end{matrix}& \begin{matrix} 0 \\ 0 \\ \end{matrix} \end{array}} \right)$
可以通过观察行最简形矩阵，其中缺失的主元的系数会当做解(如该矩阵缺失了$x_2$做主元)
将解集改写为向量空间的形式

具体操作为：在方程组中移项，保证行最简形矩阵中的主元在最左边
$\left( {\begin{array}{c|c} \begin{matrix} 1 & 1 \\ 0 & 0 \\ \end{matrix}& \begin{matrix} 0 \\ 0 \\ \end{matrix} \end{array}} \right) \implies \begin{cases} x_1+x_2=0\\ 0+0=0 \end{cases}$ $\begin{cases}x_1+x_2=0\\0+0=0\end{cases}\implies\begin{cases}x_1=-x_2\\0+0=0\end{cases}\implies\begin{cases}x_1=-x_2\\x_2=x_2\end{cases} \implies \begin{pmatrix}x_1\\x_2\end{pmatrix}=\begin{pmatrix}-x_2\\x_2\end{pmatrix}$

进一步改写为

$\begin{pmatrix}x_1\\x_2\end{pmatrix}=\begin{pmatrix}-x_2\\x_2\end{pmatrix}\implies\boldsymbol{x}=\begin{pmatrix}-x_2\\x_2\end{pmatrix}=x_2\begin{pmatrix}-1\\1\end{pmatrix}$

用$k$代替$x_2$:

$\boldsymbol{x}=x_2\begin{pmatrix}-1\\1\end{pmatrix}\xrightarrow{\quad x_2\to k\quad}\boldsymbol{x}=k\begin{pmatrix}-1\\1\end{pmatrix}$

解集为：

$\boldsymbol{x}=k\begin{pmatrix}-1\\1\end{pmatrix},\quad k\in\mathbb{R}$

如果方程组是$AB=O$，且$B$和$A$是同阶矩阵的时候，$B$的每一列都是$AB=O$的解，所以要写成是$\begin{pmatrix}-k_1&-k_2\\k_1&k_2\end{pmatrix}$的矩阵形式了

如果是$BA=O$，已知$A$的值的话，就有通过$(BA)^T=O\implies A^T B^T=O$，来求出$B$，$B$的每一行都是$BA=O$的解

当然，以上结论也可以推导至$AX=B$的情形上，如果$X$只是列向量，只需要加上特解即可，如果$B$是另一个矩阵的话，就要需要列$(A|B)$的形式，根据求基础解系的方法，分别求出每一列对应的特解，然后合并成一个矩阵，即为$X$

AX=B情况下，如果是$r(A)=r(B)=n$，即唯一解的情况，即齐次解只能为0，变换后的特解就是方程的解了，无需加上$k$

齐次线性方程组$Ax=0$的解集也称为零空间，记为$null(A)$，这是因为：

$null(A)$齐次线性方程组$Ax=0$的解集
$null(A)$一定是向量空间

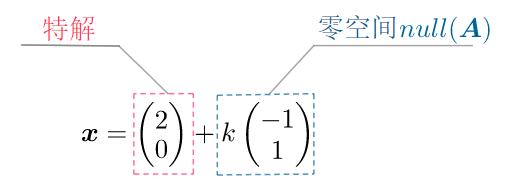
而如果是非齐次线性方程$Ax=b$的解集为：

$\boldsymbol{x}=\boldsymbol{p}+null(\boldsymbol{A})$

其中$p$为$Ax=b$的一个解，因为出现在解集中，所以是一个特殊的解，也称为特解

若两个方程组同解，说明将$A$的解集带入$B$中也完全成立，反之也成立

特解实际上只是一个能让方程成立的解，如果$Aa_1=Aa_2=b$，那么$\frac{a_1+a_2}{2}$肯定是其特解，需要根据题目条件灵活求其特解

若只有基础解系，求矩阵的最大无关组时，需要先根据基础解系列出各个向量的关系，若题目说某两个向量构成了极大无关组，则假设$\alpha _1=k\alpha_2$，先带入基础解系，然后再带入矩阵里面，观察矩阵的秩是否满足条件

秩零定理

在之前的矩阵的秩有结论：值域的维度 $≤$ 定义域的维度

比如对于矩阵$\boldsymbol{A}=\begin{pmatrix}1&1\\1&1\end{pmatrix}$，其对应的函数矩阵如下：

$\begin{array}{c|c|c|c} \hline \quad自然定义域\quad&\quad 映射法则 \quad&\quad 值域维度 \quad&\quad 到达域 \quad\\\hline\\ \quad \mathbb{R}^2 \quad&\quad \boldsymbol{A} \quad&\quad rank(\boldsymbol{A})=1 \quad&\quad \mathbb{R}^2 \quad\\ \\ \hline \end{array}$

其值域的维度就小于定义域的维度

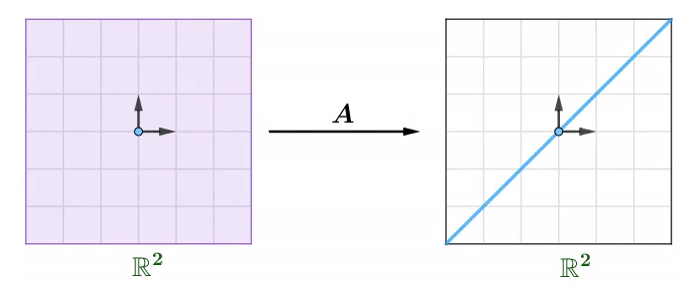
而该矩阵表示的齐次线性方程组的零空间$null(A)$，为定义域中的一条直线，被映射到值域中的0

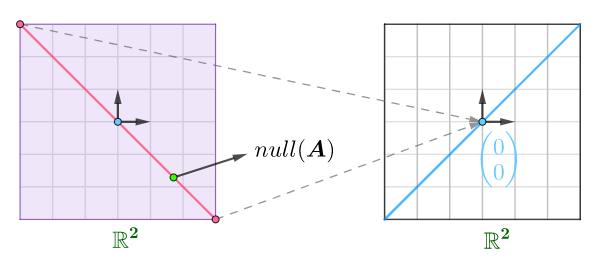
由解集的结构可知，与零空间平行的直线都会被映射为值域中的一个点

所有的直线都被缩为了点，所以导致定义域的维度缩小了一维，最终得到值域的维度为 1。用代数式表示就是：

$\underbrace{rank(定义域)}_{\large 定义域的维度}-\underbrace{rank\Big(null(\boldsymbol{A})\Big)}_{\large 零空间的维度}=\underbrace{rank(\boldsymbol{A})}_{\large 值域的维度}\implies 2-1=1$

这个结论可以推广开，即秩零定理：

对于$m×n$矩阵$A$，那么有：

$rank(\boldsymbol{A})+rank(null(\boldsymbol{A}))=n$

该定理说明矩阵的秩加上零空间的秩为定值$n$，所以该定理称为秩零定理

秩零定理显然和秩的性质：$AB=O,rank(A)+rank(B)≤n$ 一致，由秩零可以知道零空间的维度肯定是$n-r$，但是组成零空间的是$k×\alpha_1$形式的解集，当$k=0$时，显然$rank(B)$的维度就下降了。