向量

定义

$n$个有序的数所组成的数组称为$n$维向量，这$n$个数称为该向量的$n$个分量，第$i$个数$a_i$称为第$i$个分量。$n$维向量可写成一列，或一行，分别称为列向量和行向量

$n$维列向量
$\begin{pmatrix}a_1\\a_2\\\vdots\\a_n\end{pmatrix}$
$n$维行向量
$(a_1,a_2,...,a_n)\quad 或\quad \begin{pmatrix}a_1&a_2&\cdots&a_n\end{pmatrix}$

$n$也称为该向量的维数

几何意义

对于2维向量$\boldsymbol{u}=\begin{pmatrix}u_1\\u_2\end{pmatrix}$，其实就是直角坐标系中的一个点，也可以认为是原点指向$\boldsymbol{u}=\begin{pmatrix}u_1\\u_2\end{pmatrix}$的有向线段

对于3维向量，即是三维空间里面的一个点，或是原点指向它的有向线段，几何意义是等价的

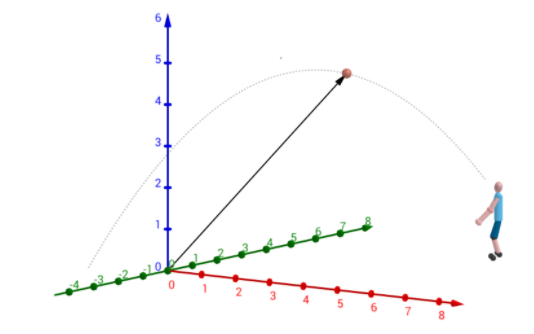
当然，这一概念可以扩展到$n$维空间中去

如果两个向量的维数相同，且各个分量相等，那么这两个向量相等

$\begin{pmatrix}1\\2\end{pmatrix}=\begin{pmatrix}1\\2\end{pmatrix},\quad\begin{pmatrix}1\\2\end{pmatrix}\ne\begin{pmatrix}2\\4\end{pmatrix}$

长度和方向

向量$u$的长度可以记作$||u||$，其方向可通过角度来表示

根据向量的长度以及角度不同，还有如下定义：

平行：方向相同或相反的两个向量称为平行，或者说两向量的夹角为$0$或$\pi$
正交：互相垂直的两个向量称为正交，或者说两向量的夹角为$\frac{\pi}{2}$
单位向量：长度为1的向量称为单位向量

零向量

$n$维向量的所有分量都是0，那么就被称为0向量

$\text{2 维零向量}:\boldsymbol{0}=\begin{pmatrix}0\\0\end{pmatrix},\qquad \text{3 维零向量}:\boldsymbol{0}=\begin{pmatrix}0\\0\\0\end{pmatrix}$

集合意义就是平面和空间中的原点

运算

将向量的加法定义为

$\boldsymbol{a}+\boldsymbol{b}=\begin{pmatrix}a_1\\a_2\\\vdots\\a_n\end{pmatrix}+\begin{pmatrix}b_1\\b_2\\\vdots\\b_n\end{pmatrix}=\begin{pmatrix}a_1+b_1\\a_2+b_2\\\vdots\\a_n+b_n\end{pmatrix}$

几何意义

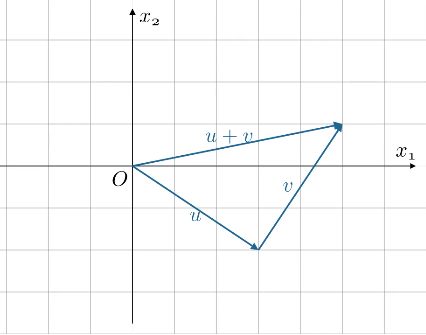
将$v$平移，使$u$，$v$首尾相接，然后就可以得到$u+v$,该方法称为三角形法则

乘法

将乘法定义为

$k\boldsymbol{a}=k\begin{pmatrix}a_1\\a_2\\...\\a_n\end{pmatrix}=\begin{pmatrix}ka_1\\ka_2\\...\\ka_n\end{pmatrix},\quad k\in\mathbb{R}$

在几何意义上，该向量$a$的各个分量都扩大了$k$倍，所以$ku$的几何意义就是对$u$进行了伸缩，其中$k$的符合决定了伸缩的方向

根据乘法的几何意义可以看出，伸缩后的向量$ku$与原向量$u$平行，所以可以借助数乘来定义平行，即如果两向量满足乘法关系，则一定平行

向量$u$的数乘为$ku$，当$k$在实数范围变动时时候，可以表示该直线$f$上所有的点

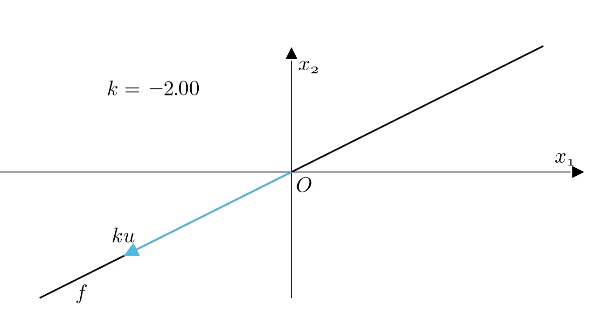
因此，直接$f$可以通过数乘来表示:

$f=k\boldsymbol{u},\quad k\in\mathbb{R}$

线性相关

若干同维数的向量$a_1,a_2,···,a_m$所组成的集合$A$，被称为向量组，记作

$\mathcal{A}:\boldsymbol{a_1},\boldsymbol{a_2},...,\boldsymbol{a_m}\quad 或\quad \mathcal{A}=\{\boldsymbol{a_1},\boldsymbol{a_2},...,\boldsymbol{a_m}\}$

给定向量组$\quad \mathcal{A}=\{\boldsymbol{a_1},\boldsymbol{a_2},…,\boldsymbol{a_m}\}$和向量$b$，如果存在一组实数$k_1,k_2,…,k_m$，使

$\boldsymbol{b_{}}=k_1\boldsymbol{a_1}+k_2\boldsymbol{a_2}+...+k_m\boldsymbol{a_m}$

则称向量$b$能被向量组$A$线性表示，或称向量$b$是向量组$A$的线性组合

显然，对于零向量，必然可以由和它同维数的向量组$A$线性表示，只需要将$k_1=0,k_2=0,\cdots,k_m=0$ 即可

给定向量组$\quad \mathcal{A}=\{\boldsymbol{a_1},\boldsymbol{a_2},…,\boldsymbol{a_m}\}$，如果存在不全为0的实数$k_1,k_2,…,k_m$，使

$k_1\boldsymbol{a_1}+k_2\boldsymbol{a_2}+...+k_m\boldsymbol{a_m}=\boldsymbol{0}$

则称向量组$A$是线性相关的，否则称为线性无关

存在不全为0的实数，意味着向量组之间是可以互相消去的，所以线性相关，如果向量组里面有0向量，那么其一定线性相关

判断矩阵线性无关的方法：

定义法
$k_1\boldsymbol{a_1}+k_2\boldsymbol{a_2}+...+k_m\boldsymbol{a_m}=\boldsymbol{0}$
通过恒等变形证明$k_1=k_2=···k_s=0$
行列式≠0以及满秩
反证法

$A$为$n$维向量组，那么：

如果$A$线性无关，则给向量组中的每个向量增加第$n+1$个分量后，该向量组依旧线性无关，或者简单叙述为：线性无关的向量组，升维后仍线性无关；
如果$A$线性相关，则去掉向量组中的每个向量的第$n$个分量后，该向量组依旧线性相关，或者简单叙述为：线性相关的向量组，降维后仍线性相关。

信息在升维时保留，但在降维时可能丢失

向量空间

定义

设$v$为一个向量组，且$v$对于向量的加法及数乘两种运算封闭，那么就称$v$为向量空间

所谓封闭，是指在$v$中向量进行数乘和加减，结果仍然在$v$中

若$\boldsymbol{a}\in \mathcal{V},\boldsymbol{b}\in \mathcal{V}$，则$a+b\in \mathcal{V}$
若$\boldsymbol{a}\in \mathcal{V},k\in \mathbb{R}$，则$\boldsymbol{ka}\in \mathcal{V}$

向量空间肯定是要包含零向量的，因为向量组肯定可以通过运算得出零向量

直线

所有一维直线构成的集合是一个向量空间，记作$R^1$:

$\mathbb{R^1}=\{(x)|x\in\mathbb{R}\}$

这个向量空间代表了全体实数

平面

所有二维向量构成的集合是一个向量空间，记作$R^2$

$\mathbb{R^2}=\{(x_1,x_2)|x_{1,2}\in\mathbb{R}\}$

这个向量空间代表了整个平面

立方体

所有三维向量构成的集合是一个向量空间，记作$R^3$

$\mathbb{R^3}=\{(x_1,x_2,x_3)|x_{1,2,3}\in\mathbb{R}\}$

这个向量空间代表了整个三维空间

向量空间并不一定是$R^n$,也可以是它们的子集。比如$R^3$，中的一个点，一根直线，或者一个面(必须经过原点)

上面提到的向量空间是$R^3$的子集，也称为$R^3$的一个子空间

$\mathcal{V}\subset \mathbb{R^3}$

更一般的，某向量组的所有的线性组合一定构成向量空间：

某向量组$\mathcal{A}=\{\boldsymbol{v_1},\boldsymbol{v_2},…,\boldsymbol{v_p}\}$,其所有线性组合构成的集合称为向量空间，也称为张成空间，记为$\mathcal{span}\{\boldsymbol{v_1},\boldsymbol{v_2},…,\boldsymbol{v_p}\}$，即

$span(\boldsymbol{v_1},\boldsymbol{v_2},...,\boldsymbol{v_p})=\{k_1\boldsymbol{v_1}+k_2\boldsymbol{v_2}+...+k_p\boldsymbol{v_p},k_{1,2,...,p}\in\mathbb{R}\}$

设两个向量组$\mathcal{A}=\{\boldsymbol{a_1},\boldsymbol{a_2},…,\boldsymbol{a_m}\}$和$\mathcal{B}=\{\boldsymbol{b_1},\boldsymbol{b_2},…,\boldsymbol{b_n}\}$，如果向量组$B$中的每个向量都能由向量组$A$线性表示，则称向量组$B$能由向量组$A$线性表示

若向量组$A$与向量组$B$能相互线性表示，则称两个向量组等价，是等价向量组

注意和矩阵的等价不同，向量组等价$\implies r(A)=r(B)$，但是$r(A)=r(B)\nRightarrow$ 向量组等价

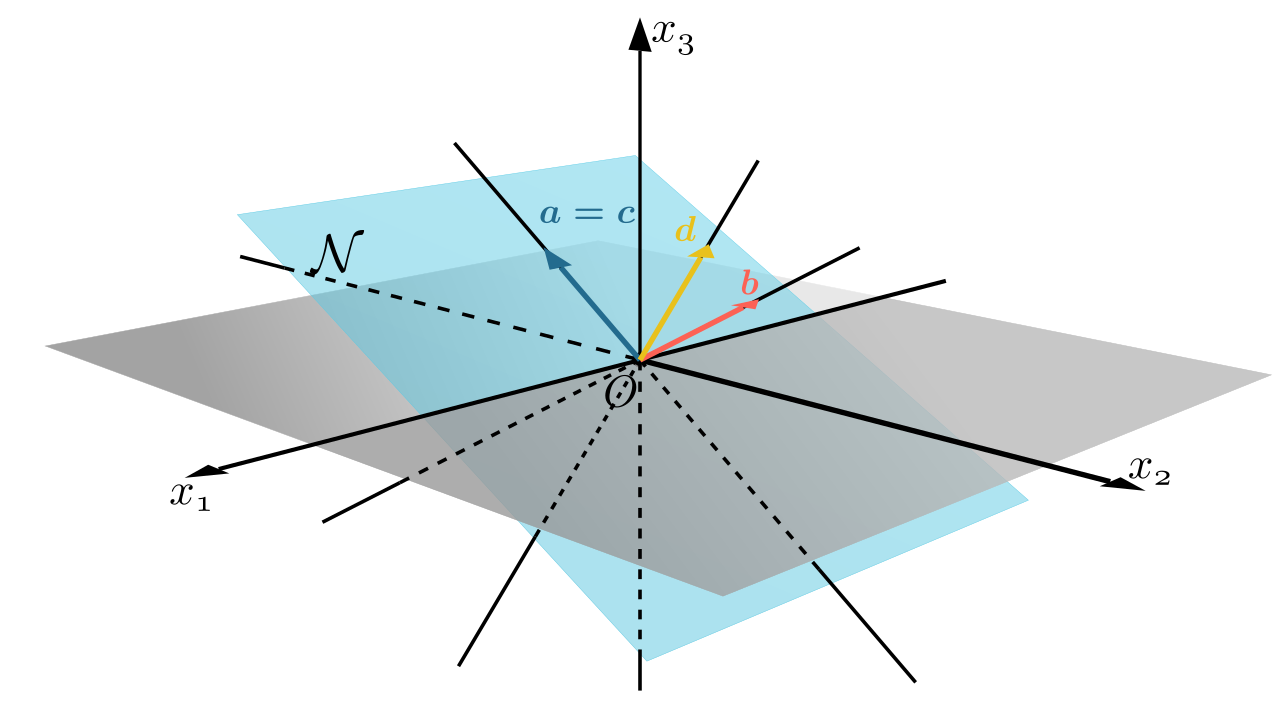
最大无关组

设有向量组$A$，如果在$A$中能选出r个向量$a_1,a_2,···,a_r$满足：

向量组$\mathcal{A_0}=\{\boldsymbol{a_1},\boldsymbol{a_2},…,\boldsymbol{a_r}\}$线性无关
向量组$A$中任意$r+1$个向量都线性相关，那么称向量组$A_0$是向量组$A$的一个最大线性无关组，简称最大无关组

如果把向量组中的向量看做搭建房子的柱子的话，向量空间就是房子，而最大无关组就是，用最少的柱子组成的向量组支撑起这个房子，也叫做该房子的基。线性相关说明某些柱子是可以被其他柱子替换的，而线性无关组就是里面的柱子都缺一不可

虽然向量组的最大无关组并不唯一，但是最大无关组包含向量的数目是相同的，此不变的数目就称为秩（rank）

假设向量组$A$的最大无关组为：

$\mathcal{A}_0=\{a_1,a_2,\cdots,a_r\}$

$A_0$的向量个数$r$称为向量组$A$的秩，记作$rank(A)$,也记作$r(A)$

不变的秩反映了向量组的复杂程度，只含有0向量的向量组，秩为0

向量空间也是向量组，这个特殊向量组的秩称为向量空间的维度，也就是最大无关组的秩

可以通过构造行最简形矩阵，主元所在的列数即是最大线性无关组的组合

向量空间的基

向量空间$v$由向量组$A$张成，如果向量组$A_0$是向量组$A$的最大无关组，那么将该最大无关组称为向量空间的基

最大无关组不是惟一的，显然对于向量空间来说，基并不唯一

有了基之后就可以对向量空间里面的向量进行定位了，或者说是，可以根据基来确定向量空间的坐标

假设$\mathcal{A}_0=\{a_1,a_2,\cdots,a_n\}$是向量空间$v$的一个基，则$v$中每个向量$x$都可通过该基唯一表示出来

$\boldsymbol{x}=k_1\boldsymbol{a_1}+k_2\boldsymbol{a_2}+\cdots +k_n\boldsymbol{a_n}$

上面的系统可以组成向量

$[\boldsymbol{x}]_\mathcal{A}=\begin{pmatrix}k_1\\k_2\\\vdots\\k_n\end{pmatrix}$

我们将其称为$x$在基$A$下的坐标向量，或者简称为$x$在基$A$下的坐标

最大无相关组才是基。零向量线性相关，所以零空间没有最大无相关组，也就是最大无相关组中向量的个数是0。空间的维度是基向量组的秩，零空间的维度是0。零空间只有零向量是任何向量空间的子集，也就是任何空间的子空间

选择不同的基，实际上就是在向量空间中建立了不同的坐标系

所有的$R^n$都有自然基，比如$R^2$的自然基就是

$\mathcal{E}:\boldsymbol{e_1}=\begin{pmatrix}1\\0\end{pmatrix},\quad \boldsymbol{e_2}=\begin{pmatrix}0\\1\end{pmatrix}$

对应的其实是直角坐标系，依次类推$R^3$的自然基就是空间坐标系

任意3维列向量可由$A$的三个特征向量线性表示 $\Leftrightarrow A$的特征矩阵$|a_1,a_2,a_3|≠0$

重要技巧：

假设向量组$A={a_1,a_2,a_3}$，如果向量$B$中的各个元素能通过$a_1，a_2，a_3$的初等列变化表示出来，那么向量组B一定能被拆分成一个矩阵和$A$的乘积

$B=AX$

在求相似矩阵，以及线性方程组的解的时候，应用非常普遍